1. Introduction
Just as endogenous growth models attempt to explain the differences in the rate of economic growth, we require a new model to explain the differences in the tax rate on capital income in each country. Chamley (1986) [1] shows that the optimal tax rate on capital income becomes eventually zero at a steady state in an one-sector dynamic general equilibrium model. This proposition is thought to be theoretically robust, and Judd (1985) [2] also shows the zero tax rate on capital income in the classical framework where there coexist capitalists and workers. In fact, however, in OECD countries, the tax rate on capital income ranges between 0.4 and 0.6 as shown in Table 1. Mankiw et al. (2009) [3] survey the optimal taxation problem and point out a large gap between theoretical results and empirical evidence. The capital income tax rate for the United States economy is far from zero. Lucas (1990) [4] points out that the tax rate on capital income in the US is accounted for 36 percent.
The difference between our model and the Chamley (1986) model is whether there exists fiscal constraint—the ratio of the government spending to GDP—the government faces. Chamley (1986) takes the level of government expenditure as given exogenously. On the other hand, our model assumes that the ratio of government expenditure to GDP is the exogenous variable and the government spending is determined endogenously by the government’s choice. The government should be anxious about the fiscal constraints. For one example, when drafting the government budget, the government is deeply concerned about the ratio of government expenditure to GDP rather than the level. For second example, when we examine the financial situations of the government in each country, comparing the ratios is much easier than the level values. For third example, the government in each country belonging to the European Union (EU) should comply with the criteria for joining the European Monetary Union. It provides that the ratio of government expenditure to GDP should be kept within a certain ratio. For final example, the political party that declared the fiscal constraints on the campaign hustings must keep the election promise after it wins by the election. We derive the positive optimal tax rate on capital income. This result from our model depends only on the discount rate, the rate of capital depreciation, and the exogenous ratio of government spending to GDP. Thus, our model plays role in the tax policy proposals at each country.
We are interested in the positive optimal tax rate. There are some literatures which derives the positive (or negative) optimal tax rate. Aiyagari (1995) [5] shows that the optimal tax rate on capital income becomes positive in the case that the uncertainty of heterogeneous agent’s labor income exists in the incomplete market model. Since the precautionary savings bring about the excessive

Table 1. The empirical tax rate on capital income at 2006 year (OECD data). Overall statutory tax rates on dividend income. Source: OECD Stat Extracts. OECD Tax Database. Part 2. Taxation of corporate and capital income (2006).
accumulation of capital stock in the model, the positive tax rate on capital income is needed to reduce capital accumulation. Correia (1996) [6] shows that the optimal tax rate on capital income does not zero if there is the production factor on which the government cannot impose taxation. Jones et al. (1993) [7] show that the optimal tax rate on human capital as well as on physical capital become zero. Chari et al. (1994) [8] shows numerically that there is a quantitative presumption that the ex ante capital tax rate is approximately zero.
We find that the empirical tax rate on capital income (Overall PIT + CIT rate)1] ranges between 0.4 and 0.6 in OECD countries. The tax rate on capital income at 2006 year (OECD data) is shown in Table 1, which indicates the overall statutory tax rates on dividend income. Let us regard the tax rate on capital income as the Overall PIT (Personal Income Tax) plus CIT (Corporate Income Tax).
Of course, the optimal tax rate must be different across countries, and it must be country-specific depending on the fiscal situation of the government in each country. In reality, there are countries such as France, Denmark, and Sweden have a large public sector (where the ratio of government expenditure to GDP is around 0.230) while there are countries such as the United States and Japan have maintained a relatively small public sector (where the ratio of government expenditure to GDP is around 0.15), as shown in Table 2. These data are constructed by dividing the real government expenditure by the real GDP. Note that the government expenditure does not include government investment in Table 2.
By injecting some parameters and the empirical ratio of the government spending to GDP in OECD countries into our theoretical results as for optimal tax rate on capital income, we can find the country-specific optimal tax rates as shown in Table 3.
Then, we can compare the theoretical optimal tax rate on capital income shown in Table 3 with the empirical value of capital income tax rate shown in Table 1. The empirical tax rate on capital income in OECD data is higher than the theoretical optimal tax rate predicted by our model. Let us present our model below.

Table 2. The ratio of the government expenditure to GDP at 2006 year (OECD data) by using real term. Source: OECD Stat Extracts, and National Accounts. Y is real GDP. G is the government expenditure in real term. G is final consumption expenditure of the general government. Note that G consists of government consumption only and does not include government investment. G/Y is the fiscal ratio except for government investment.

Table 3. The optimal tax rate on capital income predicted by our model.
2. The Model
Let us consider the optimal taxation problem in an one-sector dynamic general equilibrium model with fiscal constraint. We adopt “the primal approach to the Ramsey problem” which was developed by Lucas and Stokey (1983) [9]. The primal approach is divided into six steps. 1) The households choose consumption and leisure in order to maximize their discounted lifetime utility subject to their budget constraints. We can obtain the first-order conditions which are the Euler equation of consumption with after-tax rate of return, and the condition that the marginal rate of substitution of leisure and consumption equals to the after-tax real wage. Next, we solve the profit maximization problem of firms. These lead to the competitive equilibrium solution in private sector. Denote the competitive equilibrium solution by (CE); 2) By solving the differential equation of budget constraints of households at each time, we can obtain an intertemporal budget constraint of the households expressed in terms of present value; 3) By substituting the first-order conditions of households into the intertemporal budget constraint of households, the implementability condition is obtained; 4) By using the first-order condition from the profit maximization of the firms and their Euler’s Theorem and nonarbitrage condition, the budget constraint of the government and the households can reduce to the simple resource constraint; 5) The government maximizes the social welfare function subject to the resource constraints and the implementability condition. This leads to the Ramsey plan solution. Denote the Ramsey plan solution by (RP); 6) Search the tax rate on capital income and labor income at steady state which is compatible both in the competitive equilibrium solution (CE) and in the Ramsey plan solution (RP), respectively.
2.1. Househlds
Let us consider homogeneous households who have infinite horizon. A household maximizes the discounted lifetime utility given by
 (1)
(1)
subject to the budget constraint of an household given by
 (2)
(2)
where C is consumption, L is labor, 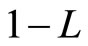 is leisure,
is leisure,  is a preference parameter weighted on the felicity by leisure,
is a preference parameter weighted on the felicity by leisure,  is discount rate, B is bond and K is capital where initial capital
is discount rate, B is bond and K is capital where initial capital 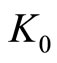 and bond
and bond  are given, r is real interest rate, rB is a rate of bond return, rk is a tax rate on capital income, and
are given, r is real interest rate, rB is a rate of bond return, rk is a tax rate on capital income, and  is a tax rate on labor income.
is a tax rate on labor income.  is an initial bond holdings. We assume that the government does not impose tax on a rate of return for the bond holding. The important two equations which generate the competitive equilibrium solution are given by
is an initial bond holdings. We assume that the government does not impose tax on a rate of return for the bond holding. The important two equations which generate the competitive equilibrium solution are given by
 (3)
(3)
 (4)
(4)
where (3) is the optimal labor supply condition that the marginal rate of substitution of leisure and consumption equals to the after-tax real wage, and (4) is the Euler equation of consumption which determine an intertemporal allocation of consumption. The non-arbitrage condition is given by 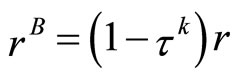 . We denote the after-tax wage rate by
. We denote the after-tax wage rate by , and the after-tax interest rate by
, and the after-tax interest rate by  . Non Ponzi Game (NPG) condition faced by household is given by
. Non Ponzi Game (NPG) condition faced by household is given by
 and Non Ponzi Game (NPG) condition faced by government is given by
and Non Ponzi Game (NPG) condition faced by government is given by
 NPG condition implies that it is prohibited to borrow infinitely. By using the budget constraints of households at each time periods (2) and NPG condition, we can obtain an intertemporal budget constraint of households expressed by present value which is given by
NPG condition implies that it is prohibited to borrow infinitely. By using the budget constraints of households at each time periods (2) and NPG condition, we can obtain an intertemporal budget constraint of households expressed by present value which is given by
 (5)
(5)
where the left-hand side of this intertemporal budget constraint is lifetime consumption, and the right-hand side is lifetime income which consists of an initial capital (which is an initial asset) and lifetime labor income.
2.2. Firms
Let us consider perfectly competitive firms. The production technology of firms satisfies the neoclassical production function expressed as  where Y is output, K is capital stock, L is Labor. The perfect competitive firms maximize the profit where R is the rental rate of capital, and
where Y is output, K is capital stock, L is Labor. The perfect competitive firms maximize the profit where R is the rental rate of capital, and  is the wage rate. The optimal conditions for the profit maximization problem implies that each factor price equals to the marginal product of its factor as follows:
is the wage rate. The optimal conditions for the profit maximization problem implies that each factor price equals to the marginal product of its factor as follows:  and
and .
.
If one household lends the capital of one unit to a firm, the firm earns the rate of return R which equals to the marginal product of capital, but the utilization of capital for production involves capital depreciation. Denote the capital depreciation rate by . The non-arbitrage condition must hold as follows:
. The non-arbitrage condition must hold as follows: .
.
2.3. The Government
The budget constraint of the government is given by
 (6)
(6)
where the left-hand side is tax revenue, and right-hand side is the government expenditure.
By combining the budget constraint of households and the government, and by using the equation of net domestic production, we can obtain the resource constraints;
 (7)
(7)
Let us impose an important assumption on the constraint of the government problem. That is, the government should be concerned with the upper limit of the ratio of the government expenditure to GDP.
We assume the fiscal constraint as follows:
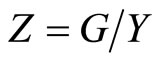 (8)
(8)
The Problem faced by the government (what is called the Ramsey Problem) is to maximize the objective function (1) subject to (3), (4), (5), (7), and (8). Without the Equation (8) in this Ramsey problem, our model reduces to the model of Chamley (1986).
2.4. Implementability Condition
By substituting the first-order condition of the households into the intertemporal budget constraint of the households, we can obtain the implementability condition as follows:
 (9)
(9)
2.5. Primal Approach to the Ramsey Problem
The Ramsey problem is to maximize the objective function (1) subject to the resource constraint (7), fiscal constraint (8), and implementability condition (9).
2.6. Solving for the Ramsey Problem
Let us set up a Lagrangian where 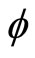 is a Lagrangian multiplier associated with the implementability condition,
is a Lagrangian multiplier associated with the implementability condition,  is a Lagrangian multiplier associated with the resource constraint, and
is a Lagrangian multiplier associated with the resource constraint, and 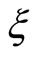 is a Lagrangian multiplier associated with our fiscal constraint. By using the formula of the integral in part, we can obtain
is a Lagrangian multiplier associated with our fiscal constraint. By using the formula of the integral in part, we can obtain

The first-order conditions of the Ramsey problem are given by
 (10)
(10)
 (11)
(11)
 (12)
(12)
 (13)
(13)
 (14)
(14)
 (15)
(15)
(10) is the condition that the marginal utility of consumption equals to the shadow value of capital (the present-value costate variable) in the Ramsey problem (RP). (11) is the condition that the marginal substitution of leisure and consumption equals to the real wage in the Ramsey problem (RP). (12) is the implementability condition, which is the crucial equation in the model of the optimal taxation problem.
By introducing the fiscal constraint, there occurs a relation output and the government spending. Since the fiscal ratio is exogenously given, an increase in output due to the increase in capital brings about the increase in the government spending, therefore the increase in the tax rate. Thus the larger fiscal ratio gives rise to the higher tax rate. An increase in capital increases the govern-ment expenditure. The households do not recognize the fiscal constraints.
Equation (13) is the condition which determines optimal government expenditure at every time periods. An increase in the fiscal ratio increases the degree of freedom of government’s behavior, while it gives rise to the crowding out of private consumption, which decreases the marginal utility of consumption. In other words, the government can increase the government expenditure due to an increase in the fiscal ratio by one unit and it can obtain the marginal utility of the government consumption, while it decreases private consumption and depresses the marginal utility of consumption, which brings about an increase in capital stock. This surplus capital stock gives rise to the increase in tax rate on capital income in order to avoid the excess capital. This is the mechanism which generates the positive tax rate on capital income in our model.
We can obtain the Euler equation from the Ramsey Problem as follows:
 (16)
(16)
By using both the condition that the marginal product of capital equals to the real rental rate, and non-arbitrage condition, and by substituting  into the Equation (16), we obtain as follows:
into the Equation (16), we obtain as follows:
 (16)’
(16)’
The conditions (10), (11), and (16) described above generate the Ramsey problem solution.
We know that the an increase in the fiscal ratio decreases the objective function (social welfare) as follows;
 .
.
3. The Optimal Tax Rate on Capital Income
Let us seek out the optimal tax rate on capital income which is compatible the Euler equation from the Ramsey problem given by
 (16)’
(16)’
with the Euler equation from the households problem (the competitive equilibrium) given by

(CE).
Therefore, the positive optimal tax rate on capital income is derived as follows.
Proposition
If we consider the one-sector dynamic optimal taxation problem with fiscal constraint, the positive optimal tax rate on capital income is derived as follows:

The essence of the paper is that under a fiscal constraint, an income tax (on both labor and capital income) is a Pigouvian tax and therefore desirable. The fact that the government must throw away a fraction of output is formally equivalent to saying that output Y produces social waste . A Pigouvian tax rate Z on production is then desirable, and this can be implemented by an income tax rate Z.
. A Pigouvian tax rate Z on production is then desirable, and this can be implemented by an income tax rate Z.
The intuition is the same as in models where the social and the private returns to capital are not the same due to externalities (as in the learning-by-doing model but of opposite sign). Here the social return to capital is lower than the private because capital also increases government spending above the optimal level (zero) and therefore the need of taxation.
The government expenditure does not enhance wellbeing of the representative household or productivity of the economy. In this regard, it is just wasteful. Then this paper establishes that the capital income tax rate is constant over time and takes strictly positive value. The intuition of the argument can be illustrated as follow. Given that a fixed portion of the output is wasted as government expenditure, social productivity of capital is lower than perceived by the household. Or instance, government spending occupies 20% of GDP and private (before tax) return on capital is 10%. The household decides an amount of his/her saving based upon the latter. However, he/she overvalues productivity of increasing capital stock whereas productivity of capital from social standpoint is 8%. 2% (=10% – 8%) is wasted resource by the government on margin. Therefore households results in accumulating excess capital more than the social optimality eventually. This surplus capital stock gives rise to the increase in tax rate on capital income in order to avoid the excess capital. This is the mechanism which generates the positive tax rate on capital income.
We adopt the empirical value shown in Table 2 as the exogenous variable of fiscal constraint and the parameter settings of  and of
and of . Substitute the exogenous values into our crucial equation:
. Substitute the exogenous values into our crucial equation:
 Then, we obtain the optimal tax rate on capital income that is appropriate for each country as in Table 3. Compare the theoretical optimal tax rate on capital income shown in Table 3 with the empirical value of the tax rate on capital income shown in Table 1. You can recognize that empirical data of the tax rate on capital income (Overall PIT plus CIT rate) are too higher than the theoretical results predicted by our model. Although our theoretical model treats with normative problem of public economics, the results predicted by our model can apply for policy proposals in each country.
Then, we obtain the optimal tax rate on capital income that is appropriate for each country as in Table 3. Compare the theoretical optimal tax rate on capital income shown in Table 3 with the empirical value of the tax rate on capital income shown in Table 1. You can recognize that empirical data of the tax rate on capital income (Overall PIT plus CIT rate) are too higher than the theoretical results predicted by our model. Although our theoretical model treats with normative problem of public economics, the results predicted by our model can apply for policy proposals in each country.
4. Conclusion
The paper has analyzed a version of Chamley’s dynamic optimal taxation problem in which the government faces fiscal constraint that requires it to spend a constant fraction of output on intrinsically worthless projects. The main theoretical result is that under the fiscal constraint the optimal tax rate on capital income becomes positive. Our model can explain the difference of the tax rate on capital income in each country. In fact, tax rate on capital income at many countries in the real world is between 0.4 and 0.6. We have tried to bridge the gap between the results of Chamley model (1986) and the empirical data of tax rate. Our model of the optimal taxation problem with fiscal constraints can succeed in generating a realistic and country-specific tax rate on capital income (0.2 to 0.4). The fiscal ratio is a key factor for tax policy of each country. Our simple prototype model for explanation of realistic tax rate can play role in tax system reform at each country. A realistic and relevant setting should be that the government spending is directed for productivity enhancing investment such as infrastructure as considered in Barro (1990) [10] in the context of endogenous growth and/or it is included in the utility of the household. In these circumstances, capital tax will serve like benefit tax. Of course, in the political economy setting, the government (or more precisely politicians and bureaucrats) may be motivated to use the government spending for own interest. The present paper is normative study of public economics.
5. Acknowledgements
I would like to thank Tamotsu Nakamura (Kobe University), Kazuo Mino (Kyoto University), Atsushi Miyake (Kobe Gakuin University), Shin Imoto (Onomichi University), Jumpei Tanaka (The University of Kitakyushu), Yunfang Hu (Tohoku University), Ryo Arawatari (Nagoya University), Keichi Morimoto (Osaka University), Yoichi Gokan (Ritsumeikan University), Daisuke Amano (Otaru University of Commerce), and Junichi Itaya (Hokkaido University) who is a commentator at the annual conference of the Japanese Economic Association (Tsukuba University, Autumn, 2011) for their very helpful comments and suggestions on previous drafts of this work. Of course, all remaining errors are mine.
NOTES