Primordial Open-System Thermodynamics and the Origin of a Biophysics Selection Principle ()
1. Introduction
Biophysics has its most distant roots in the characteristics of reaction specificity, within a context of an open system of non-equilibrium thermodynamics. In Biosystems, the entrance of energy and matter should support changes in free energy, but also prevent that formed products could re-enter into the system, allowing eventual release of its degraded form. Example: The lung-blood system.
The results of high energy physics has been reported elsewhere in terms of the characterization of particles, leaving without exploring integrative parameters between the initial and present states of nature evolution. It has been proposed that, if the flow of energy conform an interconnection between dissipative states, this could be applied to a biophysical examination of the selection principle. This is the reason why the paper characterizes the half-life of particle decay as a dissipative state. The neutrinos are characterized by their role of products which cannot reenter into the system.
If half-life is used as a parameter of the universe chronology, this treatment evidences the continuous input of energy and matter as maintaining a dissipative enthalpy describable as the source of energy evolution, without reaching equilibrium. This analogy between the high energy physics and biophysics shows that quanta evolution could be integrated as part of a thermodynamic open continuum, which branches into biophysics.
The thermodynamics state of the Universe appears to correspond with a non-equilibrium system, projection to the initial state, requires extrapolation to the quantum level. The increment of free energy to oppose entropy within a system was idealized by J. C. Maxwell as “little red demons”, indicating the need for information linkage [1] itself an energy expenditure. The latter, imply a requirement for a flow of mass and energy into and out of the system [2], this one differentiates open [3,4] from close thermodynamics.
A thermodynamic perspective allows an enthalpy increment when a particle structure “enters” into a dissipative state, de-confining energy inside a system. This one, coupled to the exit from the system of one of the reactions products like neutrinos, allow configuring nonequilibrium thermodynamics system, capable to operate like open within a self-contained Universe. A more complex model could analyze the role of zero point energy, which as a non-participant, tilts for further support of the system tendency to irreversibility.
The large difference between the half-life of each of the species of primordial particles prevents connectivity of states, allowing a symptotic irreversibility [5] and the plotting of a particle evolutionary pattern, Figure 1.
Half-life delimits changing composition of particle populations, as a parameter to characterize deconfined states of energy, contributing to enthalpy, which supports the expenditure of free energy, and associated increment of entropy, Figure 1.
Energy of activation, Ea, is a Gaussian-symmetry distribution but decayfavors kinetic asymmetry, because the reaction order is more favorable for the particle splitting

Figure 1. Plot according to their half-life: t1/2, and resting-mass: m. Particles which surge in high-energy colliders like HLC were plotted. The first band groups particles with a t1/2 around 10-22 s corresponds to strong interaction predominance. The second band groups particles with a t1/2 around 10-11 s that correspond with electroweak interaction.
into two or more particles than their tendency to collide to regenerate the original one. A particle leaking out of the interaction-system restricts the backward sense by preventing stationary states.
The overall process involves quantum decoherence and configures a chronological unidirectional function. Hence, data from the physics of particles was analyzed under the conjecture supporting an open system, could also involve a chronologic determinant fitting with Prigogine’s requirement for an operative self-selection principle [3,4].
Sakharov [6-8] stated that from an initial symmetric state, a matter-antimatter to develop asymmetry within the primordial universe, involved: I: Violation of the baryonic conservation number. II: Violation of symmetry CP strong. III: Deviations from thermodynamic equilibrium.
The primordial asymmetry [9-11] is analyzed as a function of the chronology allowing survival to annihilation of a residue of quark-antiquark. It is assumed: I. Baryon number conservation. II. Violation of electroweak CP-symmetry. III. Deviations of thermodynamic equilibrium as a function of a no-null transition time for W± bosons [12,13] and the no-electroweak-interaction of products with leak of neutrinos/antineutrinos [14,15].
2. Results
P-Parity allows reversal of helicity, a left-handed electron 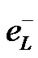 transform into right-handed positron
transform into right-handed positron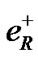 . W± bosons couple with CP-conjugate
. W± bosons couple with CP-conjugate 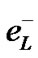 and
and 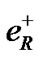 but not to C-conjugate
but not to C-conjugate  or P-conjugate
or P-conjugate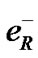 . CP-symmetry is violated in neutral K decay [16] and neutral B0 decay [17]. T symmetry violation occurs in neutral K decays [18]. These violations allow an accumulative residual of matter.
. CP-symmetry is violated in neutral K decay [16] and neutral B0 decay [17]. T symmetry violation occurs in neutral K decays [18]. These violations allow an accumulative residual of matter.
3. Characterization of Particles by Resting-Mass and Half-Life
The decay of particle populations generates an increment of enthalpy which supports free energy expenditures. The energy enters into the thermodynamics system by decay, equivalent to dissipation structures maintaining an open system in non-equilibrium.
The pattern of energy distribution suggests a chronology, by the changing population of particles showing a tendency of longer half-life: t1/2, which configures a chronological self-selection process.
The fit-plot, Figure 1, can be used as a model assimilating collider’s generated particles to dissipative states of same or similar primordial particles within cosmic chronology. Hence, the obtained tendency curve may manifest a correlation between deconfinement and reconfinement of energy acting as a pacemaker effect along cosmological time.
The first band in Figure 1 manifests the presence of the strong interaction: Mesons: Rho, r±, r0, and Omega, w0: 4 ´ 10-24 s; Phi, φ, 1.6 ´ 10-22 s; Eta prima, 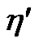 , 3 ´ 10-21 s; J/Psi, J/y, 7.2 ´ 10-21 s; Eta, h, 5 ´ 10-19 s. Baryons: Delta, D++, D±, D0, 5.58 ´ 10-24 s; Sigma, S*-(1385), 1.67 ´ 10-23 s; S*0(1385), 1.8 ´ 10-23 s; S*+(1385), 1.84 ´ 10-23 s;
, 3 ´ 10-21 s; J/Psi, J/y, 7.2 ´ 10-21 s; Eta, h, 5 ´ 10-19 s. Baryons: Delta, D++, D±, D0, 5.58 ´ 10-24 s; Sigma, S*-(1385), 1.67 ´ 10-23 s; S*0(1385), 1.8 ´ 10-23 s; S*+(1385), 1.84 ´ 10-23 s; 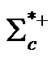 (2520), 3.9 ´ 10-23 s;
(2520), 3.9 ´ 10-23 s; 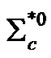 (2520), 4.1 ´ 10-23 s;
(2520), 4.1 ´ 10-23 s; 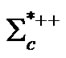 (2520), 4.4 ´ 10-23 s; Xi, X*-(1530), 6.7 ´ 10-23 s; X*0 (1530), 7.2 ´ 10-23 s;
(2520), 4.4 ´ 10-23 s; Xi, X*-(1530), 6.7 ´ 10-23 s; X*0 (1530), 7.2 ´ 10-23 s; 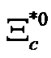 (2645), 1.2 ´ 10-22 s;
(2645), 1.2 ´ 10-22 s;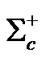 , 1.4´10-22 s;
, 1.4´10-22 s; 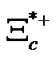 (2645), 2.1 ´ 10-22 s;
(2645), 2.1 ´ 10-22 s;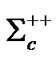 , 2.95 ´ 10-22 s;
, 2.95 ´ 10-22 s;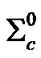 , 3 ´ 10-22 s; S0, 7.4 ´ 10-20 s; [19].
, 3 ´ 10-22 s; S0, 7.4 ´ 10-20 s; [19].
When the distance between quarks becomes very short, the intensity or interaction decreases. Hence, in between to 10-30 to 10-10 s the plasma quark-gluon would show asymptotic freedom. This mechanism allows that each quark or antiquark maintains an unstable state of attracttion with the others [19,20].
The particle sinter actvia the strong force, have halflife of 10-23 s. The strange particles, which are characterized by the electroweak interaction, have half-lives between 10-10 and 10-8 s.
Particles and antiparticles have the same spin and mass, but opposite electrical charges, and quantum numbers strangeness S, 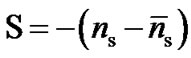 , isospin I3, lepton number L and baryonic number B. However, S+ and S- are not antiparticles have the same B = 1 and masses are not identical. Strong interaction conserves the strangeness S, but after to 10-10 s the weak interaction dominates which ignores S and I3.
, isospin I3, lepton number L and baryonic number B. However, S+ and S- are not antiparticles have the same B = 1 and masses are not identical. Strong interaction conserves the strangeness S, but after to 10-10 s the weak interaction dominates which ignores S and I3.
Recognition of the specific direction of the longitudenal-spin and handedness for neutrino emission allows selecting different reaction paths.
The released energy by short lived particle decays [21] becomes substrate of subsequent reactions.
A second band, Figure 1, results from a latter drop of temperature allowing particles in which electroweak interaction became manifest and the deconfined energy supports the creation of new particles.
As the distances between pions became greater than 1 Fermi, the energy involved by an attempt of quarks separation, becomes greater than the mass of the pions and these multiply [22]. Production of pions ,
,  ,
, 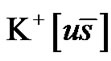 ,
, 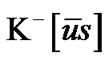 ,
,  , has been detected at 900 MeV with ALICE at the LHC [23]. These processesat primordial universe could be expected to prevent accumulation of high energy photons and favor the increase in the population of quarks and antiquarks conforming the quark-gluon plasma at 10-10 s [24].
, has been detected at 900 MeV with ALICE at the LHC [23]. These processesat primordial universe could be expected to prevent accumulation of high energy photons and favor the increase in the population of quarks and antiquarks conforming the quark-gluon plasma at 10-10 s [24].
Mesons: Pion, p0, 8.4 ´ 10-17 s; neutral D, D0 and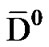 , 4.1 ´ 10-13 s; Charmed B,
, 4.1 ´ 10-13 s; Charmed B, 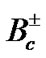 , 4.6 ´ 10-13 s; Strange D,
, 4.6 ´ 10-13 s; Strange D,  , 4.9 ´ 10-13 s; Charged D, D±, 1.04 ´ 10-12 s; Strange B,
, 4.9 ´ 10-13 s; Charged D, D±, 1.04 ´ 10-12 s; Strange B,  and
and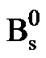 , 1.46 ´ 10-12 s; Neutral B, B0 and
, 1.46 ´ 10-12 s; Neutral B, B0 and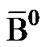 , 1.53 ´ 10-12 s; Charged B, B±, 1.63 ´ 10-12 s; Kaon-short,
, 1.53 ´ 10-12 s; Charged B, B±, 1.63 ´ 10-12 s; Kaon-short, 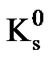 , 8.9 ´ 10-11 s; Kaons, K±, 1.24 ´ 10-8 s; Pions, π±, 2.6 ´ 10-8 s; Kaon-long,
, 8.9 ´ 10-11 s; Kaons, K±, 1.24 ´ 10-8 s; Pions, π±, 2.6 ´ 10-8 s; Kaon-long, 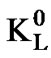 , 5.2 ´ 10-8 s. Baryons: Xi,
, 5.2 ´ 10-8 s. Baryons: Xi, 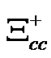 , 3.3 ´ 10-14 s; Charmed Omega,
, 3.3 ´ 10-14 s; Charmed Omega, 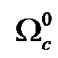 , 6.9 ´ 10-14 s;
, 6.9 ´ 10-14 s; , 1.12´10-13 s; Charmed lambda,
, 1.12´10-13 s; Charmed lambda, 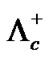 , 2 ´ 10-13 s; Charmed Xi,
, 2 ´ 10-13 s; Charmed Xi, 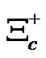 , 4.42 ´ 10-13 s; Bottom Omega,
, 4.42 ´ 10-13 s; Bottom Omega,  , 1.13 ´ 10-12 s; Bottom Lambda,
, 1.13 ´ 10-12 s; Bottom Lambda, 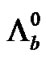 , 1.391 ´ 10-12 s; Xi,
, 1.391 ´ 10-12 s; Xi, 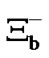 , 1.56 ´ 10-12 s; S+, 8.018 ´ 10-11 s; Omega, W-, 8.21 ´ 10-11 s; S-, 1.479 ´ 10-10 s;
, 1.56 ´ 10-12 s; S+, 8.018 ´ 10-11 s; Omega, W-, 8.21 ´ 10-11 s; S-, 1.479 ´ 10-10 s;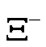 , 1.639 ´ 10-10 s; L0, 2.631 ´ 10-10 s; X0, 2.9 ´ 10-10 s, Figure 1 [19].
, 1.639 ´ 10-10 s; L0, 2.631 ´ 10-10 s; X0, 2.9 ´ 10-10 s, Figure 1 [19].
Kaons [25] K±: m = 493.7 MeV/c2 and pions π±: m = 139.6 MeV/c2, the higher half-life mesons: 1.24´10-8 s and 2.6 × 10−8 s respectively.
I.a.1. 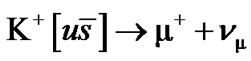 Ù
Ù 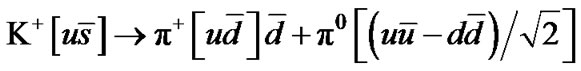
I.a.2. 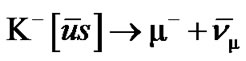 Ù
Ù 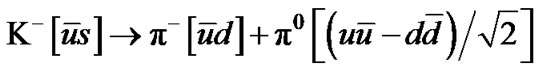
I.b.1.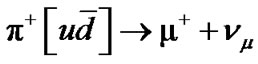 ,
, 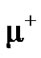 antimuon I.b.2.
antimuon I.b.2.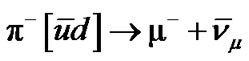 ,
,  muon At the lepton Eraoccurs the annihilation of muonsat 9 ´ 10-5 s,
muon At the lepton Eraoccurs the annihilation of muonsat 9 ´ 10-5 s, : about 200 times the electron mass [21,26].
: about 200 times the electron mass [21,26].
I.c.1. Antimuon, 2.2 × 10-6 s and 105.6 MeV/c2: 
I.c.2. Muon, 2.2 × 10-6 s and 105.6 MeV/c2: 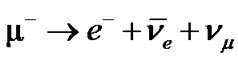
The muon-antimuon pair’s annihilation was shown to be 1% asymmetric [27,28]. This allows inferring reactions progresses from a primordial CP-violation process, at constant total energy capable to increment the relationship matter/radiation at differences steps of the chronology.
Overall assessment of the sequence allows inferring that the decay of particles produced new ones, gradually more stable. In addition, residual high-energy photons trying to separate the quark-antiquark inside mesons, allows an increment of mesons number.
4. Integration of Hadrons-Antihadrons Reactions
To approach a unitary perspective in terms of Sakharov conditions required solutions on how matter could survive pair annihilation, and to describe conditions that restrict microscopic reversibility.
This reconfinement of the energy allows to enhance of the electroweak CP-asymmetry, reported for the mesons decay [27,29], as a pathway for the predominance of matter.
Unlike the electron-positron pairs, which are abundant when the temperature is higher than their mass, protons (stable) and neutrons appear only at a temperature well below its mass (100 MeV = 1012 K), being that mass »938 MeV corresponds to 1013 K.
The residual asymmetry quark-antiquark would restrict the generation of nucleons at 4 ´ 10-5 s, the generation of antiproton and antineutron. At this time the temperature drops from 1012 K to 1010 K and density from 1014 to 104 g/cm3.
II.a. 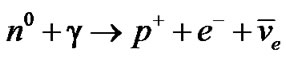
II.b. 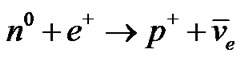
II.c. 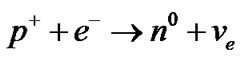
II.d. 
The first reaction shows how weak interaction is able to shift the charge of a particle. The neutron/antineutron conversion into proton/antiproton occurs with the release of antineutrinos/neutrinos restricting microscopic reversibility. The antineutrinos emission increase, because as handedness [30,31] carriers, may be produced by the reactions decreasing antimatter.
The free neutron decay, II.a.: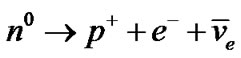 , has a half-life of 886 s. But can be activated by interaction with the energy of the environment, according to the sequence:
, has a half-life of 886 s. But can be activated by interaction with the energy of the environment, according to the sequence:
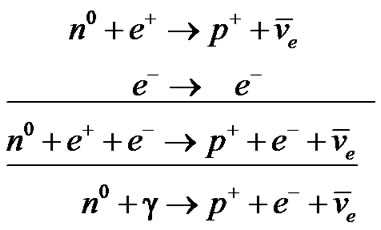
This pathway shows as a feedback the modulator effect of energy since the rhythm of gamma photon production controls the decay rate of neutrons.
The following reactions are obtained by charge symmetry and antimatter quality of reactions II [32].
III.a. 
III.b. 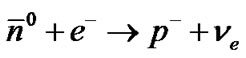
III.c. 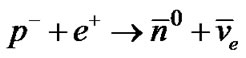
III.d. 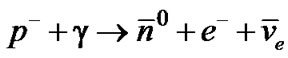
It could be diagram a sequence of reactions allowing a matter survival system:
IV.a. 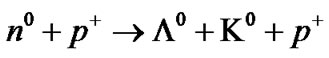
IV.b. 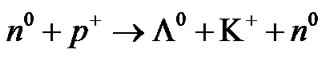
IV.c. 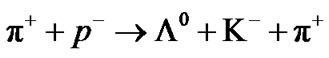
IV.d. 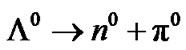
IV.f. 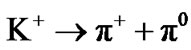
The production of hyperon requires the simultaneous productions of 2 kaons with positive strangeness number [33,34]. K± kaon decays in 1.24 ´ 10-8 s, neutral Hyperon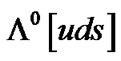 : 1115 MeV, decays in 2.6 ´ 10-10 s [35- 37]. The production of hyperon requires the simultaneous productions of 2 kaons with positive strangeness number.
: 1115 MeV, decays in 2.6 ´ 10-10 s [35- 37]. The production of hyperon requires the simultaneous productions of 2 kaons with positive strangeness number.
The symmetric reactions in the lines II and III are interconnected. Two protons interact to generate a pion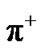 , proton
, proton  and a neutron
and a neutron 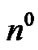 (IV.a.). A pion
(IV.a.). A pion 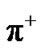 and antiproton
and antiproton 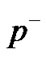 generates
generates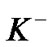 , a pion
, a pion 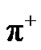 and neutral hyperon
and neutral hyperon  (IV.b.). The kaon
(IV.b.). The kaon 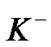 decays into a minus pion
decays into a minus pion 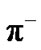 and a neutral pion
and a neutral pion 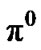 (IV.c.). The
(IV.c.). The 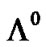 hyperon decays into a neutron
hyperon decays into a neutron 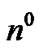 and a neutral pión
and a neutral pión 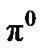 (IV.d.). In order to simplify, Figure 2, the decay of pions
(IV.d.). In order to simplify, Figure 2, the decay of pions  were not included, but are computed to show a residual:
were not included, but are computed to show a residual: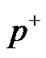 ,
, 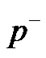 , 3
, 3 , 3
, 3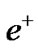 , cancelable by pairs annihilation and matter survival: 4
, cancelable by pairs annihilation and matter survival: 4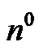 /2
/2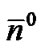 , plus: 7
, plus: 7 , 7
, 7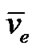 .
.
The disappearance of antinucleons: antiprotons and antineutrons, results in a residual composition of neutrons which by decay also generate protons, and neutrinos, antineutrinos, electrons and positrons.
Similar solutions could be to develop pointing to an iterative process which results in a leftover of matter and lead to the exclusion of antimatter.
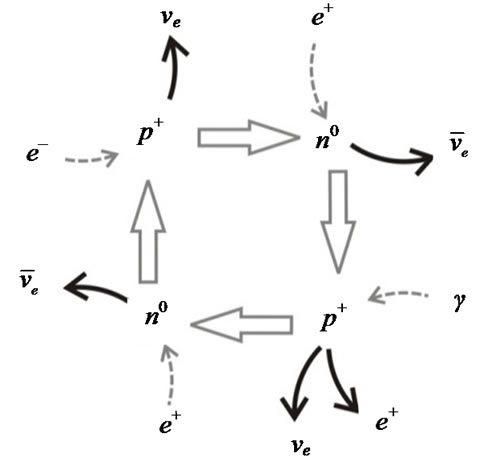
5. Cydic Interactions of Hadrons and Antihadrons to Consume Gamma Radiation plus Electrons and Positrons
The flow of reactants and products could be organized cyclically, Figure 2. If there is quantitative difference between matter and antimatter, the former could be maximized as a function of the cycle turnover. The relationship between usually accepted total numbers of neu-
 (a)
(a)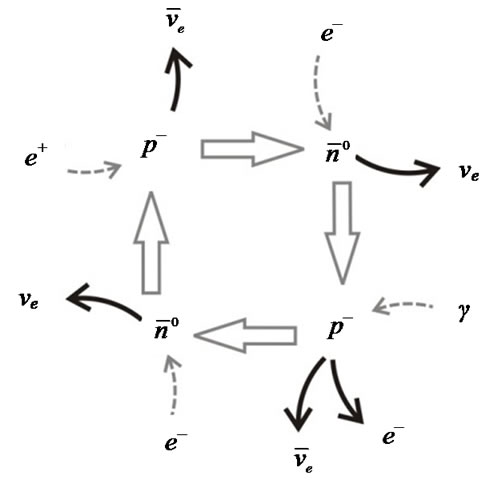 (b)
(b)
Figure 2. Coupling between reactions allows cycles (a) Hadrons; and (b) Antihadrons. The balances show that in both cases one electron and one positron are consumed, to absorb gamma radiation, generating two neutrinos and two antineutrinos. Hence, allowing coupling to consume gamma radiation from the residual balance.
trinos 1087 versus number of baryons 1078 suggests that the estimate excess of neutrinos may be related to turnover number.
Figure 2 shows that an excess of electrons and positrons, with 10-7 s to their annihilation, could instead be absorbed as hadrons or antihadrons with a production of neutrinos and antineutrinos. Also the photons could be consumed in quantities much higher than the hadrons presents in the system. The hadrons/antihadrons recycling could support a near stationary state of the ratio: 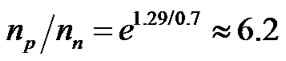 [20].
[20].
However, starting at 2 s, the free neutron decays to achieve stability through the synthesis of deuterium, 200 s.
The annihilation of electron-positron pairs starts at activation temperature 0.511 MeV at 4 s. The pairs are nolonger relativistic and annihilate as photons increasing their temperature: . The numeric resolution for a Boltzmann equation for annihilation electronpositron shows that the equilibrium lasted at
. The numeric resolution for a Boltzmann equation for annihilation electronpositron shows that the equilibrium lasted at 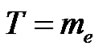 continuing to
continuing to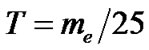 , where
, where 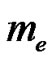 is electron mass. This process leaves a negligible positron residue as a cold fossil and the electrons resulting from the matter-antimatter interaction. When
is electron mass. This process leaves a negligible positron residue as a cold fossil and the electrons resulting from the matter-antimatter interaction. When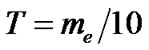 , remain 1 per 1000 initial pairs.
, remain 1 per 1000 initial pairs.
6. Decay of Particles and System Irreversibility
The Figure 1 shows that the regression curve, delimits tendency of the strong and weak forces at about: Fermi 10-13 cm (3 × 10-24 s). It is inferred that a particle-lacking period, required the surging of electroweak forceintermediate vectors bosons W±, to generate more stable populations of particles. W± connectivity 10-14 cm (3 × 10-25 s) allows a differentiable interaction, without fragmentation, of polarized helicities at flavor scenarios inside the quarks sea.
Single longitudinal-spin asymmetries violate parity: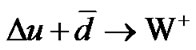 ,
,  , and are sensitive to flavor the antimatter plus matter:
, and are sensitive to flavor the antimatter plus matter: ,
,
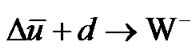 . This electroweak lepton-antilepton pairs involves g - Z0 interference and the production of W± [38].
. This electroweak lepton-antilepton pairs involves g - Z0 interference and the production of W± [38].
The reaction, 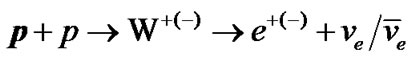 , sensitive to helicity allows either one of the bosons W± decay emitting electron or positron. Therefore, the reaction conserves CP-symmetry.
, sensitive to helicity allows either one of the bosons W± decay emitting electron or positron. Therefore, the reaction conserves CP-symmetry.
Feynman schemes show color inter-conversion in the decay neutron®proton trough the transition d ® u. The diagram of Figure 3 shows decay in kinetics and thermodynamics terms [39] to illustrate irreversibility parameters and that the reverse reaction is a differentiable and separate pathway. The very short half-life of W± allows that the transition energy dissipate and prevents the mass-action of products. The peaks represent delocalized energy transition at successive steps of the reactions.
The ordinate axis shows the energy release during exothermic conversion d ® u involves the loss of resting mass 5.6 MeV ® 2.3 MeV, which appears as kinetic energy added as inertial mass of the emitted electron.
The mediator particles 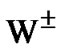 show recognition of helicity-handedness. Therefore quantity:
show recognition of helicity-handedness. Therefore quantity: , yield a mirror representation of the disintegration of antineutron:
, yield a mirror representation of the disintegration of antineutron: 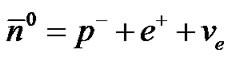 \
\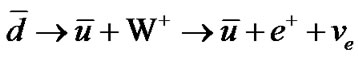 , Figure 4.
, Figure 4.
A dotted curve in Figure 4 indicates a much shorter half-life of the transition states which in this context prevents the reversibility of products into substrate. The scale is based on the resting mass of two down quarks (d) of 5 MeV each and one up (u) of 2 MeV. (*) Excited or transitions states. The arrow ↑ indicates that the emission of electrons and antineutrinos escape from the system.
Figure 3 shows a reaction produced in the extreme