Magnetization Performance of LDPC Reduced-Complexity Decoding Algorithms ()
Low-density parity-check (LDPC) codes are very efficient for communicating reliably through a noisy channel. N.Sourlas [1] showed that LDPC codes, which revolutionize the codes domain and used in many communications standards, can be mapped onto an Ising spin systems. Besides, it has been shown that the Belief-Propagation (BP) algorithm, the LDPC codes decoding algorithm, is equivalent to the ThoulessAnderson-Palmer (TAP) approach [2]. Unfortunately, no study has been made for the other decoding algorithms. In this paper, we develop the Log-Likelihood Ratios-Belief Propagation (LLR-BP) algorithm and its simplifications the BP-Based algorithm and the λ-min algorithm with the TAP approach. We present the performance of these decoding algorithms using statistical physics argument i.e., we present the performance as function of the magnetization.
1. Introduction
Low-density parity-check (LDPC) codes were first discovered by Gallager [3], in his thesis, in 1962 and have recently been rediscovered by Mackay and Neal [3,4]. These codes can get very close to the Shannon limit by mean of an iterative decoding algorithm called BeliefPropagation (BP) algorithm [5].
This performance combined with their relatively simple decoding algorithm makes these codes very attractive for the next generation of digital transmission systems. Indeed, these codes have been chosen as a standard for the second Satellite Digital Video Broadcasting normalization (DVB-S2). So, the search for efficient implementations of decoding algorithms is being a challenge.
The implementation of the BP algorithm is difficult. That’s why different simplifications of this algorithm were discovered. The BP algorithm can be simplified using the BP-Based algorithm [6] and the λ-min algorithm [7].
N. Sourlas [1] has shown in 1989 that there is a mathematical equivalence of error-correcting codes to some theoretical spin-glass models. This analogy has contributed to the present proximity of the statistical physics and the information theory. Therefore, the methods of statistical physics developed in the study of disordered systems proved to be efficient for studying the properties of these codes. One of these methods is the Thouless-AndersonPalmer (TAP) [2] approach which is shown equivalent to the BP algorithm by kabashima, et al. [8]. Unfortunately, no study has been made for the other decoding algorithms.
In this paper, we develop the Log-Likelihood RatiosBelief Propagation (LLR-BP), the BP-Based and the λ-min decoding algorithms with the TAP approach. Their performance is evaluated as a function of a statistical physics parameter which is the magnetization.
This paper is organized as follows. Section 2 corresponds to a general description of the LDPC codes and their decoding algorithm. Section 3 describes the similarity between the BP algorithm and the TAP approach. In Section 4, we develop the LLR-BP algorithm and its simplifications the BP-Based algorithm and the λ-min algorithm with the TAP approach. Finally and before concluding, simulation results as function of the magnetization are presented in Section 5.
2. LDPC Codes and Decoding Algorithm
2.1. Low-Density Parity Check Codes
Binary LDPC codes, are linear block codes defined by a sparse parity check matrix , where
, where denotes the codeword length and
denotes the codeword length and 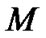 the number of paritycheck equations.
the number of paritycheck equations.
Using a notation similar to that in [4,6], let 
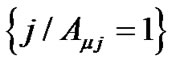 denote the set of bit
denote the set of bit  that participate in check
that participate in check . Similarly, we define the set of checks in which bit
. Similarly, we define the set of checks in which bit  participates as
participates as . We denote a set
. We denote a set with bit
with bit 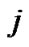 excluded by
excluded by , and a set
, and a set  with parity check
with parity check  excluded by
excluded by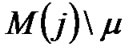 . Finally,
. Finally,  denotes the transmitted codeword.
denotes the transmitted codeword.
2.2. Belief Propagation Algorithm
This section summarizes according to [4,5], the iterative decoding of LDPC codes based on the BP algorithm. The likelihood of  is given by
is given by , with
, with  P(sj = a).
P(sj = a).
Let  denotes the probability that bit
denotes the probability that bit  of
of  is
is , given the information obtained via checks other than check
, given the information obtained via checks other than check . The quantity
. The quantity  is meant to be the probability of check
is meant to be the probability of check  is satisfied if bit
is satisfied if bit 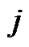 of
of  is considered fixed at
is considered fixed at  and the other bits have a separable distribution given by the probabilities
and the other bits have a separable distribution given by the probabilities 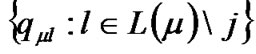 [6].
[6].
The standard iterative decoding algorithm based on the BP approach consists on the following main steps.
• Initialization: The variables  and
and  are initialized to the values
are initialized to the values 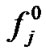 and
and 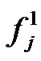 respectively.
respectively.
• Iterative processing:
1) Define  and for each
and for each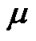 ,
,  , and for
, and for , compute
, compute
2) 
3) For each 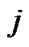 and
and , and for
, and for  update
update


where  and
and  are chosen such that
are chosen such that
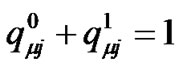 and
and 
4) Create the word  the detection of the transmitted codeword such that:
the detection of the transmitted codeword such that:

If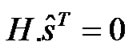 the decoding process ends. Otherwise, we pass to another iteration of BP. A failure is declared and the decoding process ends if the number of iterations exceeds the maximum number of iterations and
the decoding process ends. Otherwise, we pass to another iteration of BP. A failure is declared and the decoding process ends if the number of iterations exceeds the maximum number of iterations and  is not a valid codeword.
is not a valid codeword.
3. Decoding Problem from Statistical Physics Point of View
3.1. Statistical Physics Analogy
In the previous section, we have described the LDPC codes using the additive Boolean group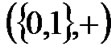 . However, in order to apply methods of statistical physics, it is convenient to introduce an equivalent group, the multiplicative binary group
. However, in order to apply methods of statistical physics, it is convenient to introduce an equivalent group, the multiplicative binary group 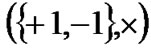 [1].
[1].
From a statistical physics point of view, the code can be regarded as a spin system. Each bit 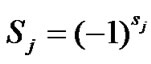 is called a spin and takes values in
is called a spin and takes values in 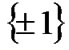 and the word
and the word  can be seen as a collection of
can be seen as a collection of  spins, called a configuration. The parity-check matrix gives rise to the interactions between the spins [1].
spins, called a configuration. The parity-check matrix gives rise to the interactions between the spins [1].
The decoding problem depends on posteriori like  where
where  is the evidence (received message or syndrome vector). By applying Bayes’ theorem this posteriori can be written in the form [1].
is the evidence (received message or syndrome vector). By applying Bayes’ theorem this posteriori can be written in the form [1].
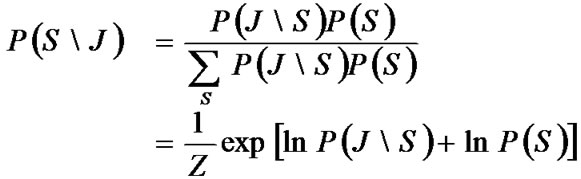 (1)
(1)
In the statistical physics description, the probability (1) can be expressed as a Boltzmann distribution at the inverse temperature  [9].
[9].
 (2)
(2)
where  is the Hamiltonian of the system.
is the Hamiltonian of the system.
In this Hamiltonian, we identify two components that are necessary for the analysis of LDPC codes.
• A term that guarantees that all parity checks are satisfied. It can be written with the Kronecker’s delta  [1].
[1].

According [9], the ’s can be replaced by a soft constraint.
’s can be replaced by a soft constraint.

where .
.
• A prior term that provides some statistical information on the dynamical variables . It can be represented by the prior distribution
. It can be represented by the prior distribution

where  is the external field. It is determined by the flip rate
is the external field. It is determined by the flip rate  of channel noise as
of channel noise as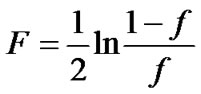 .
.
So, the Hamiltonian  is written as follows:
is written as follows:

where  is the muti-spin coupling.
is the muti-spin coupling.
3.2. Decoding in the Statistical Physics
The decoding process corresponds to finding local magnetization at the inverse temperature ,
,  and calculating estimates as [1].
and calculating estimates as [1].
 (3)
(3)
The decoding performance in the statistical physics approach can be measured by the magnetization [1] defined by the overlap between the actual message and estimate:

Here the overage  is performed over the matrices
is performed over the matrices . This value provides information about the typical performance of the code.
. This value provides information about the typical performance of the code.
The Magnetization is an order parameter which has a standard of judgment whether the whole system exhibits an ordered state or not.
• If  the system is in an ordered phase called ferromagnetic phase.
the system is in an ordered phase called ferromagnetic phase.
• If 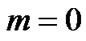 the system is in a disordered phase called paramagnetic phase.
the system is in a disordered phase called paramagnetic phase.
Two main methods can be employed for calculating the value of the magnetization: the replica method for diluted systems [9] and the TAP approach [8]. In this paper, we are interested only on the TAP approach.
3.3. TAP Approach
Kabashima, et al. [8] have shown the similarity between equations derived from the TAP [2] approach and those obtained from BP. The fields  correspond to the mean influence of sites other than the site
correspond to the mean influence of sites other than the site 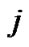 and the fields
and the fields represent the influence of
represent the influence of 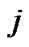 back over the system (reaction fields) [10].
back over the system (reaction fields) [10].
The similarity can be exposed by observing that the likelihood  is proportional to the Boltzmann weight [11]
is proportional to the Boltzmann weight [11]

The conditional probability  can be seen as a normalized effective Boltzmann weight (effective Boltzmann probability) obtained by fixing the bit
can be seen as a normalized effective Boltzmann weight (effective Boltzmann probability) obtained by fixing the bit  [10]
[10]

Since spin variable  takes only two values
takes only two values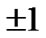 , it is convenient to express the BP/TAP algorithm using spin averages
, it is convenient to express the BP/TAP algorithm using spin averages  and
and  rather than the distributions
rather than the distributions  and
and  themselves. We use
themselves. We use  to denote
to denote . Similar notation
. Similar notation  is used for
is used for . Additionally, it was shown in [10] that the following statements hold
. Additionally, it was shown in [10] that the following statements hold
 (5)
(5)
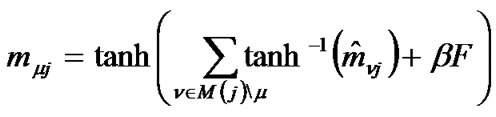 (6)
(6)
The pseudo-posteriori can then be calculated
 (7)
(7)
This provides a way for computing the Bayes optimal decoding as follows:
 (8)
(8)
The result that  is demonstrated as follows:
is demonstrated as follows:
 (9)
(9)
4. LLR-BP Algorithm and its Simplifications with TAP Approach
4.1. LLR-BP Algorithm with TAP Approach
In the LLR-BP algorithm instead of handling probabilities as in [3,5] we are going to deal with the LLRs. In practice, using LLRs as messages offers implementation advantages over using probabilities or likelihood ratios because multiplications are replaced by additions and the normalization step is eliminated [11].
In this section, we try to develop the LLR-BP with the TAP approach. Let  and
and  be the LLR of bit
be the LLR of bit 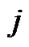 which are sent from bit node
which are sent from bit node  to check node
to check node  and from the check node
and from the check node  to bit node
to bit node , respectively. From the statistical physics definition, the LLR is defined as follows [12]:
, respectively. From the statistical physics definition, the LLR is defined as follows [12]:
 (10)
(10)
And
 (11)
(11)
We need also the following results
 (12)
(12)
Like in (12), the variable  can be also written as:
can be also written as:
 (13)
(13)
So, from Equations (5), (12) and (13) we have
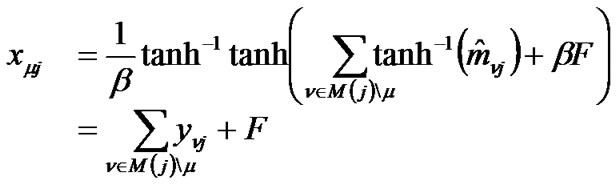 (14)
(14)
Also,  can be written as
can be written as
 (15)
(15)
Finally, the posteriori LLR of bit  is
is
 (16)
(16)
It’s not easy to implement (15) which has the form of a product. Our idea is to decompose the check node update into sign and magnitude processing like in [13]. We have from (15)
 (17)
(17)
Replacing  by
by  and
and  by
by  in (17) yields
in (17) yields
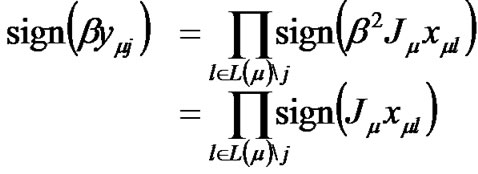 (18)
(18)
 (19)
(19)
Let  be defined by
be defined by
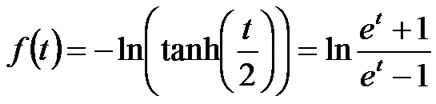 (20)
(20)
Then, taking the logarithm of the inverse of both sides of (19) yields
 (21)
(21)
The Equation (20) verifies
 (22)
(22)
So the Equation (21) can be written
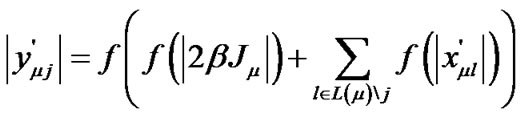 (23)
(23)
Using (10) and (11), the Equation (23) can be written as
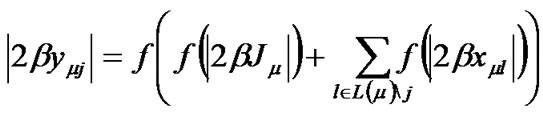 (24)
(24)
From (18) and (24), the check node processing in the statistical physics is denoted by
 (25)
(25)
4.2. BP-Based with TAP Approach
In this section, we try to develop the approximation of the BP algorithm: the BP-Based [6] algorithm, with the TAP approach. The key idea of this algorithm is that . The inequality is clear while depicting the function
. The inequality is clear while depicting the function on the Figure 1.
on the Figure 1.
The Equation (24) is then approximated by
 (26)
(26)
So, the extrinsic information in the BP-Based algorithm written with the TAP equation is given by:
 (27)
(27)
Therefore, there is an important simplification in the BP-Based algorithm with TAP approach since the check node update is replaced by a selection of the minimum input value.
4.3. λ-min Algorithm with TAP Approach
In this section, we try to develop the λ-min algorithm [7] with the TAP approach. In the check node update of (25), the magnitude processing is run using the function defined by (20). While depicting this function on the Figure 1, it is clear that 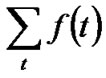 can be approximated by the maximal values of
can be approximated by the maximal values of  which is obtained for the minimal values of
which is obtained for the minimal values of .
.
So, like Guilloud, et al. [7] we propose to compute (24)with only the λ bits that participate in check  and which have the minimum magnitude.
and which have the minimum magnitude.
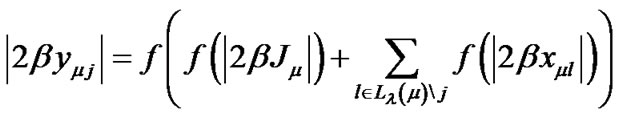 (28)
(28)
With  be the subset of
be the subset of  which contains the λ bits that participate in check
which contains the λ bits that participate in check  which
which  have the smallest magnitude.
have the smallest magnitude.
The extrinsic information in the λ-min algorithm written with the TAP equation is given by (29)
 (29)
(29)
Two cases will occur: if the bit  belongs to the subset
belongs to the subset , then
, then  are processed over
are processed over  values of
values of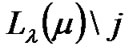 , otherwise
, otherwise  are processed over the λ values of
are processed over the λ values of . Hence, for the second case, the computations have to be performed only once [13].
. Hence, for the second case, the computations have to be performed only once [13].
5. Simulation Results
Simulations have been performed using regular (3,6) LDPC code of length  and with 20 decoding iterations. We averaged the results over 10 codes. This ensemble of LDPC code is characterized by the same block length, the ones in each column and the ones in each row. For each run, a fixed code is used to generate 1008 bit codeword from 504 bit message. Corrupted versions of the codeword are then decoded using LLR-BP, BP-Based and λ-min decoding algorithms.
and with 20 decoding iterations. We averaged the results over 10 codes. This ensemble of LDPC code is characterized by the same block length, the ones in each column and the ones in each row. For each run, a fixed code is used to generate 1008 bit codeword from 504 bit message. Corrupted versions of the codeword are then decoded using LLR-BP, BP-Based and λ-min decoding algorithms.
To observe the effect of the simplification in (27) and (29) on the performance from a statistical physics point of view, we have calculated the overlap between the actual message and the estimate (magnetization) for each fixed code and for each algorithm. After, we average the obtained results for the 10 different codes. Figure 2 depicts the magnetization performance of the LLR-BP, BP-Based and the λ-min algorithms.
According the results of Figure 2, we can conclude the effectiveness of the λ-min algorithm. At a magnetization of 0.9, the BP-Based algorithm introduces a degradation of 0.5 dB with 20 iterations. The 2-min algorithm introduces a degradation of 0.3 dB. The performance of the 3-min algorithm is slightly worse than that of the LLR-BP algorithm, the degradation is only 0.08 dB.
Another remark from Figure 2 is that at high signal to noise ratio the magnetization is concentrate at the value . This value corresponds to the ferromagnetic state in the statistical physics and to the perfect decoding in the information theory.
. This value corresponds to the ferromagnetic state in the statistical physics and to the perfect decoding in the information theory.
The analogy between the Bit Error Rate (BER) performance and the magnetization performance can be examined in [14].
6. Conclusions
In this paper, we have been interested in the decoding of LDPC codes from a statistical physics approach. First, we have examined the correspondence between LDPC codes and Ising spin systems. The relation between the BP algorithm and TAP approach is investigated. Then, we showed that LLR-BP algorithm and its simplification i.e. the BP-Based algorithm and the λ-min algorithm can be obtained using the TAP approach of Ising spin systems in statistical physics. Besides, we have presented the performance of the decoding algorithms using a statistical physics parameter which is the magnetization.
Finally, we concluded that the BP-Based algorithm reduces the complexity for updating extrinsic information but there is degradation in performance compared to the LLR-BP algorithm. The λ-min algorithm reduces the complexity for updating extrinsic information without degradation in performance compared to the LLR-BP algorithm especially when λ increases. These results con-

Figure 2. Magnetization performance of the LLR-BP, BPBased and λ-min algorithms with λ = {2, 3}, for the (1008, 3, 6) LDPC code ensemble and with 20 decoding iterations.
firm with the results obtained in the information theory.
As a perspective of our work, we propose to study the replica method. This is a method from the statistical physics applied to find the magnetization. Besides, we propose to simplify the equations of this method by the same approximation in the BP-Based algorithm and the λ-min algorithm in order to compare the analytic results with the experimental ones.
[1] N. Sourlas, “Spin-Glass Models as Error-Correcting Codes,” Nature, Vol. 339, No. 6227, 1989, pp.693-695.
[2] D. J. Thouless, P. W. Anderson and R. G. Palmer, “Solution of Solvable Model of A Spin Glass,” Philosophical Magazine, Vol. 35, No. 3, 1977, pp. 593-601.
[3] R. G. Gallager, “Low-Density Parity-Check Codes,” M.I.T. Press, Cambridge, Massachusetts, 1963.
[4] D. J. C. Mackay and R. M. Neal, “Near Shannon Limit Performance of Low Density Parity Check Codes,” Electronics Letters, Vol. 32, No. 18, 1996, pp.1645-1646.
[5] D. J. C. Mackay, “Good Error-Correcting Codes Based on Very Sparse Matrices,” IEEE Transactions on Information Theory, Vol. 45, No. 2, 1999, pp. 399-431.
[6] M. P. C. Fossorier, M. Mihaljevic and I. Imai, “Reduced Complexity Iterative Decoding of Low Density Parity Check Codes Based on Belief Propagation,” IEEE Transactions on Communications, Vol. 47, No. 5, 1999, pp. 673-680.
[7] F. Guilloud, E. Boutillon and J. L. Danger, “λ-Min Decoding Algorithm of Regular and Irregular LDPC Codes,” Proceedings of 3rd International Symposium on Turbo Codes & Related Topics, Brest, 2003, pp. 451-454.
[8] Y. Kabashima and D. Saad, “Belief Propagation vs. TAP for Decoding Corrupted Messages,” Europhysics Letters, Vol. 44, No. 5, 1998, pp. 668-674.
[9] T. Murayama, Y. Kabashima, D. Saad and R. Vicente, “Statistical Physics of Regular Low-Density Parity-Check Error-Correcting Codes,” Physical Review E, Vol. 62, No. 2, 2000, pp. 1577-1591.
[10] R. Vicente, D. Saad and Y. Kabashima, “Finite-Connectivity Systems as Error-Correcting Codes,” Physical Review E, Vol. 60, No. 5, 1999, pp. 5352-5366.
[11] J. Chen, A. Dholakia, E. Eleftheriou, M. Fossorier and X. Y. Hu, “Reduced-Complexity Decoding of LDPC Codes,” IEEE Transactions on Communications, Vol. 53, No. 8, 2005, pp. 1288-1299.
[12] M. Mezard and A. Montanari, “Information, Physics and Computation,” Oxford University Press, Oxford, 2008.
[13] F. Guilloud, “Generic Architecture for LDPC Codes Decoding,” PhD Thesis, ENST Paris, 2004.
[14] M. Abdelhedi, O. Hamdi and A. Bouallegue, “Magnetization Performance of LDPC Decoding Algorithms,” International Journal of Information and Coding Theory, 18 March 2010.