New Unique Common Fixed Point Results for Four Mappings with Ф-Contractive Type in 2-Metric Spaces ()
1. Introduction
There have appeared many unique common fixed point theorems of mappings with some contractive condition on 2-metric spaces. But most of them held under subsidiary conditions [1-3], for examples: commutativity of mappings or uniform boundness of mappings at some point, and so on. In [4-8], the author obtained similar results for infinite mappings with generalized contractive or quasi-contractive conditions under removing the above subsidiary conditions. These results generalized and improved many same type unique common fixed point theorems.
In this paper, by introducing a new class Ф, we will discuss the existence problem of unique common fixed points for four mappings with Ф-contractive type on noncomplete 2-metric spaces without any subsidiary conditions. The obtained main results in this paper further generalize and improve the corresponding results.
Here, we give some well known concepts and results.
Definition 1.1. ([4]) A 2-metric space 
consists of a nonempty set X and a function 
such that
1) for distant elements
, there exists an 
such that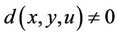
;
2) 
if and only if at least two elements in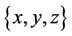 
are equal;
3)
, where 
is any permutation of
;
4) 
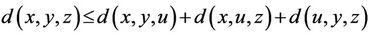for all
.
Definition 1.2. ([4]) A sequence 
in 2-metric space 
is said to be cauchy sequence, if for each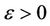 
there exists a positive integer 
such that 
for all 
and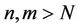
.
Definition 1.3. ([4,5]) A sequence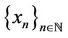 
is said to be convergent to
, if for each
,
.
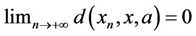And write 
and call x the limit of
.
Definition 1.4. ([4,5]) A 2-metric space 
is said to be complete, if every cauchy sequence in X is convergent.
Definition 1.5. ([9,10]) Let f and g be self-maps on a set X. If 
for some
, then x is called a coincidence point of f and g, and w is called a point of coincidence of f and g.
Definition 1.6. ([11]) Two mappings 
are weakly compatible if, for every
, holds fgx = gfx whenever 
Lemma 1.7. ([6-8]) Let 
be a 2-metric space and 
a sequence. If there exists 
such that 
for all 
and
, then 
for all
, and
is a cauchy sequence.
Lemma 1.8. ([6-8]) If 
is a 2-metric space and sequence
, then
for each
.
Lemma 1.9. ([9,10]) Let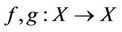 
be weakly compatible. If f and g have a unique point of coincidence
, then w is the unique common fixed point of f and g.
2. Main Results
Denote Ф the set of functions 
satisfying the following conditions: 
is continuous and increasing in each coordinate variable, and 
and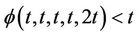 
for all
.
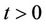Examples Let 
be defined by
where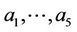 
are non-negative real numbers satisfying
.
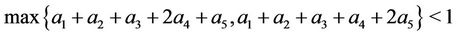Then obviously,
.
The following theorem is the main result in this present paper.
Theorem 2.1. Let 
be a 2-metric space, S, T, I, 
four single valued mappings satisfying that 
and
. Suppose that for each
,
(1)
where 
and
. If one of 
and 
is complete, then T and I, S and J have an unique point of coincidence in X. Further, 
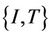and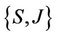 
are weakly compatible respectively, then S, T, I, J have an unique common fixed point in X.
Proof Take any element
, then in view of the conditions 
and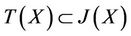
, we can construct two sequences 
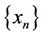and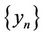 
as follows:
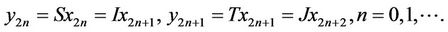(2)
For any 
(3)
If
, then by (1) and Ф, we have that
(4)
which is a contradiction since
, hence 
. And therefore, (3) becomes that
(5)
If there exists an 
such that
, then (5) becomes
which is a contradiction since
, hence we have that 
for all
. So by (5) and Ф, we obtain that
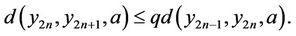(6)
Similarly, we can prove that
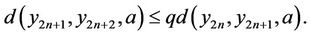(7)
Hence we have that
(8)
So 
is a Cauchy sequence by Lemma 1.7.
Suppose that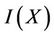 
is complete, then there exists 
and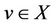 
such that
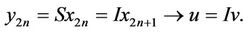(If 
is complete, there exists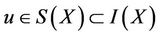
, then the conclusions remains the same.)
Since
and 
is Cauchy sequence and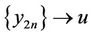
, we obtain that
.
For any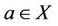
,
Let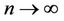
, then the above becomes
If 
for some
, then we obtain that
which is a contradiction since
. Hence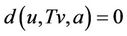 
for all
, so
, i.e., u is a point of coincidence of T and I, and v is a coincidence point of T and I.
On the other hand, since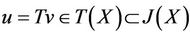
, there exists 
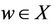such that 
By (1), for any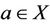
,
Let
, then we obtain that
If 
for some
, then the above becomes that
which is a contradiction since 0 < q < 1, so 
for all
. Hence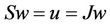
, i.e., u is a point of coincidence of S and J, and w is a coincidence point of S and J.
If 
is another point of coincidence of S and J, then there exists 
such that
, and we have that
which is a contradiction. So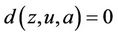 
for all
, hence
, i.e., u is the unique point of coincidence of S and J. Similarly, we can prove that u is also unique point of coincidence of T and I.
By Lemma 1.9, u is the unique common fixed point 
and 
respectively, hence u is the unique common fixed point of S, T, I, J.
If 
or 
is complete, then we can also use similar method to prove the same conclusion. We omit the part.
Here, we give only one of particular forms of theorem 2.1, which itself also generalize and improve many known results.
Theorem 2.2. Let 
be a 2-metric space, S, T, I, 
four single valued mappings satisfying that 
and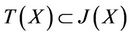
. Suppose that for each
,
where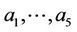 
are non-negative real numbers satisfying
.
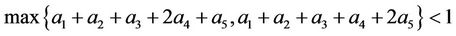If one of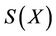
, 
, 
and 
is complete, then T and I, S and J have an unique point of coincidence in X. Further, 
and 
are weakly compatible respectively, then S, T, I, J have an unique common fixed point in X.
Proof Take 
satisfying
and let
.
Then obviously, 
, hence q and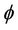 
satisfy all conditions of Theorem 2.1, so the conclusion follows from theorem 2.1 Using Theorem 2.1, we give the following contractive or quasi-contractive versions of Theorem 2.1 for two mappings.
Corollary 2.3 Let 
be a 2-metric space, 
two single valued mappings satisfying that for each
,
where 0 < q < 1 and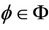
. If one of 
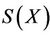and 
is complete, then T and S have an unique common fixed point in X.
Proof Let
, then by Theorem 2.1, there exist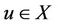 
such that u is the unique point of coincidence of S and J. But obviously S and J are weakly compatible, so u is the unique fixed point of S by Lemma 1.9. Similarly, u is also unique fixed point of T, hence u is the unique common fixed point of S and T.
Corollary 2.4 Let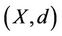 
be a complete 2-metric space, 
two single valued surjective mappings satisfying for each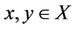
,
where 
and
, then I and J have an unique common fixed point in X.
Proof Let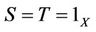
, then by Theorem 2.1, there exist 
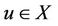such that u is the unique point of coincidence of S and J. But obviously S and J are weakly compatible, so u is the unique fixed point of J by Lemma 1.9. Similarly, u is also unique fixed point of I, hence u is the unique common fixed point of I and J.
NOTES