Mixed Convection Boundary Layer Flow over a Vertical Flat Plate with Radiative Heat Transfer ()
1. Introduction
Mixed convection (or combined convection), one of the transport phenomena, is the composition of both natural and forced convection flow. These flow patterns are discovered simultaneously by both an external forcing mechanism and internal volumetric forces. The interaction of mixed convection with thermal radiation has increased greatly during the last decade owing to its importance in many practical applications. However, in the literature the simplest physical model of such a flow is the two-dimensional laminar mixed convective flow along a vertical flat plate, extensive studies of which had been conducted by Sparrow, Eichorn and Gregg [1], Merkin [2], Lloyd and Sparrow [3], Wilks [4], Tingwei, Bachrum and Dagguent [5] and Raju, Liu and Law [6]. It has, generally, been recognized that,  (where Grx is the Grashof number and Rex is the Reynolds number) is the governing parameter for the laminar boundary layer forced-free convective flow, which represents the ratio of buoyancy forces to the inertial forces inside the boundary layer. However, forced convection exists when the limit of
(where Grx is the Grashof number and Rex is the Reynolds number) is the governing parameter for the laminar boundary layer forced-free convective flow, which represents the ratio of buoyancy forces to the inertial forces inside the boundary layer. However, forced convection exists when the limit of  goes to zero, which occurs at the leading edge, and the free convection limit can be reached if
goes to zero, which occurs at the leading edge, and the free convection limit can be reached if  becomes large. Gebhart, Jaluria, Mahajan and Sammakia [7] replaced the exponent of the Reynolds number by other values close to two in order to correlate their experimental results.
becomes large. Gebhart, Jaluria, Mahajan and Sammakia [7] replaced the exponent of the Reynolds number by other values close to two in order to correlate their experimental results.
Heat transfer for sufficiently high temperature surfaces needs a simultaneous analysis of the influence of several kinds of heat transfer mechanisms. One such mechanism through which heat can be transferred more rapidly is by the absorption, emission and scattering of radiation by the fluid. Radiation effects are important in context of space technology and processes involving high temperatures, Ozisik [8], Sparrow and Cess [9], Cess [10] and Arpaci [11] first studied the interaction of thermal radiation and natural convection which has been confined to the case of a vertical semi-infinite plate. Later, considering the Rosseland diffusion approximation, investigations on the natural convection flow as well as on the mixed convection flow of an optically dense gray viscous fluid past or along heated bodies of different geometries, such as, vertical and horizontal flat plate, cylinder, sphere, wavy surface and axisymmetic rotating and non-rotating bodies under different boundary conditions have been accomplished by Hossain, Kutubuddin and Pop [12], Hossain, Anghel and Pop [13], Hossain and Munir [14], Hossain and Rees [15], Molla and Hossain [16] and Siddiqa, Asghar and Hossain [17]. In these analysis consideration has been given to gray gases that emit and absorb but do not scatter thermal radiation. Very recently, Siddiqa, Asghar and Hossain [18] investigated the effects of thermal radiation on mixed convection flow of an optically dense viscous fluid along a vertical porous plate. In their analysis the usual Boussinesq approximation is ignored and all the physical quantities are considered to be constant except the fluid density, which exponentially vary with temperature. On the other hand, heat transfer can also be determined for a non-absorbing medium in which radiation absorption, emission and scattering processes are neglected and the surface of the object uniformly emits into the surrounding medium a constant thermal flux, which is carried off as convective-conductive and radiative components. In this regard, Martynenko, Sokovishin and Shapiro [19] examined the influence of thermal radiation on the natural convective flow of a vertical surface situated in a non-absorbing medium. Later, Salomatov and Puzyrev [20] investigated the influence of thermal radiation on the laminar natural and forced convection boundary layer flow of a nonabsorbing fluid with variable thermo-physical properties flowing around a heat emitting surface and obtain the solutions for the small and large values of thermal radiation parameter. Further, Sokovishin and Shapiro [21] analyzed the effect of thermal radiation on natural convective heat liberation from the surface of a vertical cylinder located in a transparent medium. They adopted finite difference method in order to obtain the solution of the problem in terms of Nusselt number.
Here, mixed convection flow along a semi-infinite vertical plate due to thermal radiation from the surface is analyzed in a non-absorbing medium which is not considered yet to the best of authors knowledge. It has been considered that object is located in the optically transparent medium and processes of radiation absorption, emission and scattering are neglected. It is however noted that the relationship between convection and thermal radiation is developed with the help of a boundary condition of second kind on the thermally radiating vertical surface. It needs to mention here that in radio electronic devices the measurement of the thermal regimes necessitate the inquiry of energy transfer from high temperature elements to the surrounding medium. Moreover, it is also necessary to examine not only the influence of transverse curvature on heat transfer but also the interaction of various forms of heat transfer while calculating heat liberation from the surfaces of bodies of semiconductor devices, thermo-resistors, micro-conductors etc. Particularly, in the field of electronics the transfer of thermal energy to an immobile medium is in practice with the help of two modes, namely, natural convection and radiation. Therefore, present study also aims to look at the simultaneous effects of thermal radiation and mixed convection in a nonabsorbing medium. The governing boundary layer equations are reduced to parabolic partial differential equations due to the introduction of primitive variable formulation (PVF) which are then integrated numerically by employing straightforward finite difference method in contrast with Gaussian elimination method. Numerical results thus obtained are expressed graphically in terms of local skin friction and local Nusselt number coefficients with effect of physical parameters, such as modified Richardson number (or mixed convection parameter), Ri*, surface radiation parameter, R, and Prandtl number, Pr. Furthermore, thermal energy distribution is also drawn in terms of heatlines which is well known tool used for the visualization of the flow patterns.
2. Mathematical Formulation
Consider the steady two dimensional mixed convection flow of a viscous incompressible gas along a semi-infinite vertical heated surface situated in the optically transparent medium. In addition, the processes of radiation absorption, emission and scattering are neglected. Further assume that 1) the temperature and the velocity of the free-stream is T∞ and u∞ respectively; and 2) the surface temperature of the flat plate, Tw, is sufficiently higher than the ambient fluid temperature, T∞.
Thus the fundamental boundary layer equations under the usual Boussinesq approximation for steady flow may now be written as
 (1)
(1)
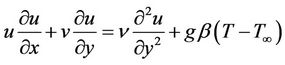 (2)
(2)
 (3)
(3)
where u, v are the velocity components in the x and y directions respectively, ν the kinematic coefficient of viscosity, g identifies the gravitational force, β the coefficient of thermal expansion, α the thermal diffusivity and T the temperature of the fluid in the thermal boundary layer. The coordinate system and the flow configuretion of the problem are shown in Figure 1.
The present work also consider that the vertical surface transmit uniform thermal flux, qw, into the surrounding medium. Moreover, the relationship between convection and thermal radiation is developed with the help of a
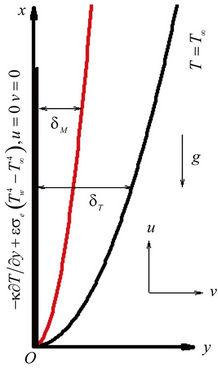
Figure 1. Physical model and coordinate axis.
boundary condition of second kind on the vertical surface which is supposed to be a gray diffusion radiator with emissivity ε. The radiative heat flux component on the wall is expressed with the help of Stefan-Boltzmann law. Therefore the boundary conditions can be written as (see [19]).
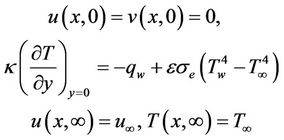 (4)
(4)
where σe is the Stefan-Boltzmann constant and κ the thermal conductivity of the fluid.
In order to obtain the governing equations in dimensionless dependent and independent variables, we introduce the following parameters
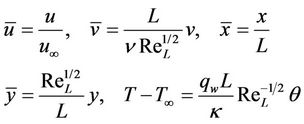 (5)
(5)
where  is the dimensionless Reynolds number and L the characteristic length of the vertical surface.
is the dimensionless Reynolds number and L the characteristic length of the vertical surface.
Substituting the variables given in (5) into the Equations (1)-(4), the following set of dimensionless governing equations (dropping bars) are obtained
 (6)
(6)
 (7)
(7)
 (8)
(8)
The boundary conditions to be satisfied are
 (9)
(9)
where
 (10)
(10)
In Equation (10) Ri is the mixed convection parameter or sometimes called buoyancy parameter (or Richardson number). It can be observed that for Ri > 0 (Tw > T∞) we have assisting buoyancy flow in which Ri accelerates the fluid motion whereas for Ri < 0 (Tw < T∞) the flow is termed as opposing buoyancy flow. Further, in case when Ri = 0 we have purely forced convection flow in which buoyancy effects are not present. R is the surface radiation parameter that measures the ratio of total heat flux transported from the surface of the wall to the radiative component. Moreover, ξ is termed as radiative length parameter that measures the degree of intensity of the ratio of radiative component and Reynolds number. It should be noted that for ξ = 0 the surface becomes nonradiating. Thus ξ establishes the connection between the radiative and convective components of the heat flux. The dimensionless Prandtl number, Pr, calculates the strength of momentum diffusivity to the thermal diffusivity.
The method of solution of the present problem posed through the set of Equations (6)-(9) follows after adopting the primitive variable formulation (PVF) which is discussed below.
3. Solution Methodologies
In this section, primitive variable formulation is initiated to reduce the boundary layer Equations (6)-(9) into a set of parabolic equations which are integrated by applying straightforward finite difference method together with Gaussian elimination technique. It should be noted that parabolic equations are obtained for 1) the entire range of Ri* (=Ri/ξ3, the modified Richardson number); 2) the region where Ri* is small and 3) the region in which Ri* is termed as large.
3.1. Solution for Small Ri* ( 1)
1)
For small Ri*, the region is termed as forced convection dominated regime. So, for this region following group of transformations can be adopted
 (11)
(11)
Substituting (11) in Equations (6)-(9) one obtains
 (12)
(12)
 (13)
(13)
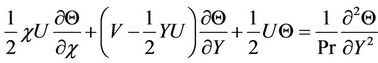 (14)
(14)
The corresponding boundary conditions are
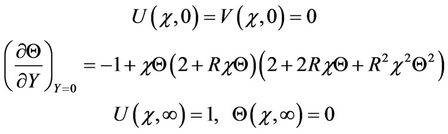 (15)
(15)
Once the quantities U and Θ and their derivatives are evaluated, one can calculate local skin friction coefficient,  and local Nusselt number coefficient
and local Nusselt number coefficient 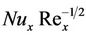 which are significant from engineering point of view. Below are the expressions for these physical quantities, respectively.
which are significant from engineering point of view. Below are the expressions for these physical quantities, respectively.
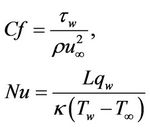 (16)
(16)
where τw and qw are the dimensional skin friction and heat flux at the plate respectively, and are defined as
 (17)
(17)
Using the transformations given in Equations (5) and (11), in order to acquire the following dimensionless expressions for the coefficients of local skin friction and local Nusselt number, respectively.
 (18)
(18)
It can be seen, from the relations given in (18) that the local skin friction coefficient and the local Nusselt number coefficient varies locally with the parameter, χ. Further, the equations valid for large Ri* are now obtained with the help of appropriate transformations.
3.2. Solution for Large Ri* ( 1)
1)
It is observed that the region away from the leading edge of the surface is dominated by natural convection flow. So, for this region governing equations can be obtained with the help of following group of transformations
 (19)
(19)
Introducing the transformation given in (19) into the Equations (12)-(15) in order to obtain the following governing equations for large Ri*.
 (20)
(20)
 (21)
(21)
 (22)
(22)
The corresponding boundary conditions are
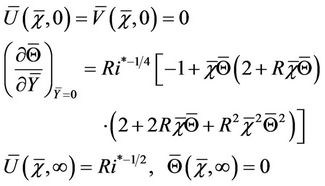 (23)
(23)
It can be noted that for large Ri*, the physical quantities like local skin friction coefficient,  , and local Nusselt number coefficient,
, and local Nusselt number coefficient,  , can be respectively evaluated from the expressions given below.
, can be respectively evaluated from the expressions given below.
 (24)
(24)
Likewise, the equations valid for all values of Ri* are now obtained in the following subsection.
3.3. Solutions for All Ri*
In order to obtain a system of equations applicable to the entire regime of modified Richardson number (or mixed convection parameter), Ri*, we compare the transformations (11) and (19) and obtain
 (25)
(25)
and, hence, a convenient switching from one system to the other. Introducing the above transformation in the Equations (12)-(15) to acquire the following governing equations for entire values of Ri*.
 (26)
(26)
 (27)
(27)
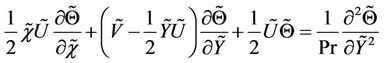 (28)
(28)
Boundary conditions are
 (29)
(29)
For entire range of Ri*, the physical quantities of interest like local skin friction coefficient,  , and local Nusselt number coefficient,
, and local Nusselt number coefficient,  , can be presented respectively from the following expressions.
, can be presented respectively from the following expressions.
 (30)
(30)
The system of Equations (12)-(15), (20)-(23), (26)-(29) are solved numerically by employing straightforward finite difference method. For this, discretization process is initiated and central-difference quotients are used for diffusion terms whilst backward difference quotients are employed for the convective terms. Finally a system of algebraic equations is obtained as given below.
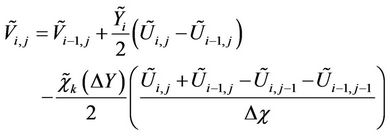 (31)
(31)
 (32)
(32)
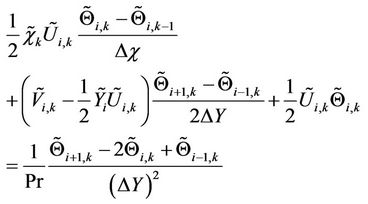 (33)
(33)
for  and
and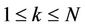 . Subscripts i and k represent the grid points along the
. Subscripts i and k represent the grid points along the  and
and  direction, respectively; whereas
direction, respectively; whereas  and
and 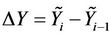 are the step size in their respective directions. The boundary conditions take the form
are the step size in their respective directions. The boundary conditions take the form
 (34)
(34)
where P1 = Ri*/(1 + Ri*), P2 = (1 + Ri*)−1/4 and P3 = (1 + Ri*)−1/2 for all Ri*. However, for sufficiently small and large values of Ri* the expressions for Pi’s i = 1, 2, 3 can be taken as P1 = Ri*, P2 = 1 and P3 = 1 and P1 = 1, P2 = Ri*−1/4 and P3 = Ri*−1/2, respectively.
The computation has been started from  and then it marched up to
and then it marched up to 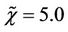 taking the step length
taking the step length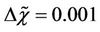 . At every
. At every  station, the computations are iterated until the difference of the results of two successsive iterations become less or equal to 10−6. By compareing the results for different grid size in
station, the computations are iterated until the difference of the results of two successsive iterations become less or equal to 10−6. By compareing the results for different grid size in  direction, we reached at the conclusion to choose
direction, we reached at the conclusion to choose  and maximum value is taken to be
and maximum value is taken to be  in order to get accurate results. Very recently, this method has been used successfully by Siddiqa, Asghar and Hossain [22] in order to investigate high Prandtl number effects on the natural convection flow over an inclined flat plate with internal heat generation and variable viscosity. Molla, Hossain and Gorla [23] also used this numerical scheme, efficiently, to study natural convection boundary layer flow over a vertical wavy frustum of a cone in the presence of thermal radiation.
in order to get accurate results. Very recently, this method has been used successfully by Siddiqa, Asghar and Hossain [22] in order to investigate high Prandtl number effects on the natural convection flow over an inclined flat plate with internal heat generation and variable viscosity. Molla, Hossain and Gorla [23] also used this numerical scheme, efficiently, to study natural convection boundary layer flow over a vertical wavy frustum of a cone in the presence of thermal radiation.
4. Heat Function
Heatlines is the well known tool which is broadly used to show the paths followed by heat. Thus it gives a well bordered and non-crossed passageway where heat flows. The heat function  for two-dimensional boundary layer flow in Cartesian coordinates was defined by Morega and Bejan [24] while studying the forced convection flow in the boundary layer region. The particular dimensional relation for the heat function
for two-dimensional boundary layer flow in Cartesian coordinates was defined by Morega and Bejan [24] while studying the forced convection flow in the boundary layer region. The particular dimensional relation for the heat function 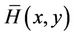 which is valid within the boundary layer is (see [24]):
which is valid within the boundary layer is (see [24]):
 (35)
(35)
 (36)
(36)
where ρ is the density of the fluid, cp the specific heat at constant temperature, κ the thermal conductivity and T0 the lowest temperature in the boundary layer region which is taken to be T0 = T∞. It can be noted that the term 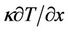 is not present in Equation (36), as the boundary layer approach neglects the longitudinal x diffusion when compared with the longitudinal convection. This does not represent any limitation from the general heat function formulation (see Kimura and Bejan [25]), as the term
is not present in Equation (36), as the boundary layer approach neglects the longitudinal x diffusion when compared with the longitudinal convection. This does not represent any limitation from the general heat function formulation (see Kimura and Bejan [25]), as the term  can be considered and ultimately taken as zero at the end of the development. It is convenient to introduce the following dimensionless heat function H
can be considered and ultimately taken as zero at the end of the development. It is convenient to introduce the following dimensionless heat function H
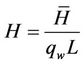 (37)
(37)
Due to (5) and (37) the dimensional heat gradient Equations (35)-(36) becomes (dropping bars)
 (38)
(38)
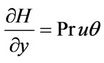 (39)
(39)
The analytical expressions for heat function H(x, y) can be obtained by defining the following forms
 (40)
(40)
Conclusively, using (11) and (40) in Equations (38)- (39) and doing some algebraic manipulations we get the following analytical expressions for heat functions
 (41)
(41)
It can be observed that relation (41) is valid for small values of Ri*. Further, one can firmly noted from the analytical expression of the function G(Y) in (41) that heat transfer processes are simultaneously governed by heat convection  and conduction
and conduction 
phenomena. It is further seen from the Equation (41) that numerical values of the heat function are closely associated with the total Nusselt number. That is why they are important tools to analyze, as a whole, the heat transfer processes.
Likewise, expressions for large and all values of Ri* can be obtained by using the relations (19) and (25) respectively. These relations comes out to be:
 (42)
(42)
and
 (43)
(43)
respectively.
5. Results and Discussion
In the present investigation, the effect of thermal radiation on mixed convection flow along a semi-infinite vertical plate is analyzed in the nonabsorbing medium. The vertical plate is located in the optically transparent medium and particularly the processes of radiation absorption, emission and scattering are neglected. The relationship between convection and thermal radiation is however established with the aid of second kind of boundary condition on the thermally radiating vertical surface. The interaction of various forms of heat transfer is much important while calculating heat liberation from the surfaces of bodies of semiconductor devices, thermo-resistors, micro-conductors etc. Keeping this in mind, the present study is initiated. A group of continuous transformation is applied on the dimensionless equations in order to obtain the parabolic partial differential equations for the regimes where modified Richardson number, Ri*, 1) is small; 2) is large; and 3) ranges from 0 to ∞. The system of equations thus obtained for small, large and all values of Ri* are integrated numerically by employing straightforward finite difference method in contrast with Gaussian elimination method. The resultant numerical solutions are depicted graphically in terms of local skin friction and local Nusselt number coefficients with effect of various physical parameters, such as, mixed convection parameter, Ri*, and surface radiation parameter, R, for low Prandtl number fluids. Moreover, thorough study of thermal energy distribution is also given in terms of heatlines which are significantly used to visualize the flow patterns.
The literature survey shows that for a 8 N sulphuric acid (1.9 mhos/in) with moderate temperature difference i.e. ΔT = 50˚F, a magnetic field of 25,000 gauss would be needed to get the considerable effect on heat transfer rate. Formation of such an extensive amount of magnetic field may not be considered outside the range of ordinary laboratory practice. Similarly, for salt water (0.64 mhos/ in), equivalent amount of strength of magnetic field is required in order to see the influence of heat transfer. However in the case of gases, electrical conductivities of technically interesting magnitudes are not achieved until the gas temperatures are very high. For example, even at a temperature of 5500˚F and a density corresponding to 100,000 ft altitude (l/70 of standard sea level density), the electrical conductivity of air is only about 10−4 mhos/in. For these circumstances, a strength of about 20,000 gauss magnetic field is sufficient to significantly effect the free convection heat transfer. The combination of such high temperatures and high magnetic fields is difficult to achieve and is not commonly encountered. However, moderate temperatures and comparatively smaller magnetic fields would be required if the air were seeded with potassium. At the other end of the scale from these illustrations is the case of liquid metals. For liquid mercury (2.5 × 104 mhos/in), a 25 percent reduction in the local heat flux can be achieved with a magnetic field of 1000 gauss for ΔT = 50˚F. Thus, it would seem that among all the fluids, the liquid metals appear to be most susceptible to the effects of a magnetic field (see Sparrow and Cess [26]). One can analyze the significance of liquid metals in the nuclear field where it is used extensively in the conception of fission and fusion reactions. Specifically in nuclear fusion lithium or lithium alloys allow to merge the fuel generation problem with the heat removal from the fusion reaction. For power plants which are exerted at extensively high temperature, sodium is treated as heatengine fluid. Hence, because of technical importance and tempting applications in industries, the present investigation deals with small Prandtl number, Pr, i.e., Pr = 0.05 (that is appropriate for lithium).
Further, discussion has been carried out on the numerical results which are obtained in terms of coefficient of local skin friction, 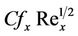 , and coefficient of local Nusselt number,
, and coefficient of local Nusselt number,  , for several parameters that controls the underlying physical situation.
, for several parameters that controls the underlying physical situation.
5.1. Effect of Physical Parameters R, Ri* and χ on Coefficients of Local Skin Friction and Local Nusselt Number
The influence of surface radiation parameter, R is discussed initially on local skin friction coefficient,  , and local Nusselt number coefficient,
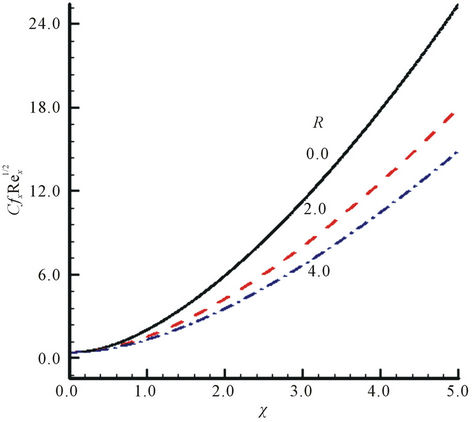
, and local Nusselt number coefficient,  , in Figure 2 for R = 0.0, 2.0, 4.0 while other parameters are Pr = 0.05 and Ri* = 10.0. It can be seen from these figures that coefficient of local skin friction and coefficient of local Nusselt number decreases considerably owing to the increase in the surface radiation parameter, R. Physically it happens due to the reason that R is acting as source term which increases energy at the vicinity of the fluid and as a result coefficients of local skin friction and local Nusselt number enhances. In addition, Figures 2(a) and (b) show that momentum as well as thermal boundary layer thicknesses decreases signifycantly as R enhances.
, in Figure 2 for R = 0.0, 2.0, 4.0 while other parameters are Pr = 0.05 and Ri* = 10.0. It can be seen from these figures that coefficient of local skin friction and coefficient of local Nusselt number decreases considerably owing to the increase in the surface radiation parameter, R. Physically it happens due to the reason that R is acting as source term which increases energy at the vicinity of the fluid and as a result coefficients of local skin friction and local Nusselt number enhances. In addition, Figures 2(a) and (b) show that momentum as well as thermal boundary layer thicknesses decreases signifycantly as R enhances.
Further, the variation of local skin friction coefficient,  , and local Nusselt number coefficient,
, and local Nusselt number coefficient, 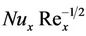 , is inspected for Ri* = 10.0, 50.0, 100.0 and 150.0 whereas Pr = 0.05 and R = 2.0 in Figure 3. One can observe that wall shear stress increases substantially as buoyancy force is intensified. However, opposite effects are examined on the rate of heat transfer. Physically it happens due to the reason that Ri* > 0 acts like supportive driving force which accelerates the fluid flow with in
, is inspected for Ri* = 10.0, 50.0, 100.0 and 150.0 whereas Pr = 0.05 and R = 2.0 in Figure 3. One can observe that wall shear stress increases substantially as buoyancy force is intensified. However, opposite effects are examined on the rate of heat transfer. Physically it happens due to the reason that Ri* > 0 acts like supportive driving force which accelerates the fluid flow with in
 (a)
(a) (b)
(b)
Figure 2. (a) Variation of local skin friction and (b) Local Nusselt number with χ for R = 0.0, 2.0, 4.0 while Pr = 0.05 and Ri* = 10.0.
 (a)
(a) (b)
(b)
Figure 3. (a) Variation of local skin friction and (b) Local Nusselt number with χ for Ri* = 10.0, 50.0, 100.0, 150.0 while Pr = 0.05 and R = 2.0.
the boundary layer and consequently skin friction enhances and heat transfer rate reduces significantly.
Likewise in Figure 4 the effect of surface radiation parameter, R, and locally varying parameter, χ, is shown graphically on local skin friction coefficient,  and local Nusselt number coefficient,
and local Nusselt number coefficient,  against the modified Richardson number Ri* which ranges from 0.0 to 20.0. In this figure R takes the values 0.0 and 0.5 and χ is equal to 1.0 and 2.0 for the Prandtl number Pr = 0.05. It is observed that both coefficient of local skin friction and coefficient of local Nusselt number enhances considerably owing to the increase in the value of χ. In this figure the graphs are compared for small, large and
against the modified Richardson number Ri* which ranges from 0.0 to 20.0. In this figure R takes the values 0.0 and 0.5 and χ is equal to 1.0 and 2.0 for the Prandtl number Pr = 0.05. It is observed that both coefficient of local skin friction and coefficient of local Nusselt number enhances considerably owing to the increase in the value of χ. In this figure the graphs are compared for small, large and
 (a)
(a) (b)
(b)
Figure 4. (a) Variation of local skin friction and (b) Local Nusselt number with Ri* for χ = 1.0, 2.0, R = 0.0, 0.5 while Pr = 0.05.
all values of modified Richardson number, Ri*, and an excellent agreement is observed. Figure clearly indicates that flow develops more rapidly as χ increases from 1.0 to 2.0, therefore, locally varying parameter, χ, plays important role in the establishment of the fluid flow and motion of the fluid increases as locally varing parameter, χ, increases. However the effect of surface radiation parameter is different. Due to the increment in R, it is observed that shear stress decreases in magnitude while rate of heat transfer gets stronger within the boundary layer. This depreciation in magnitude of skin friction coefficient happens due to the stronger influence of modified Richardson number, Ri*, on the fluid flow.
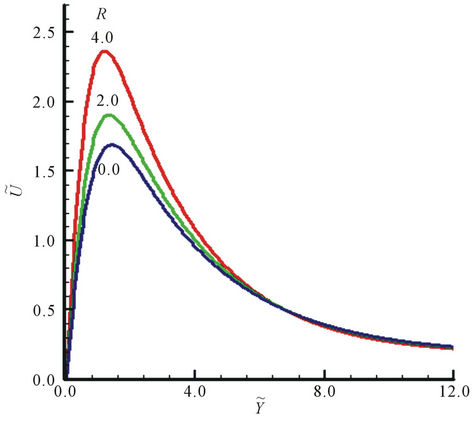
5.2. Effect of R on Velocity and Temperature Profiles
Temperature and velocity profiles are also plotted in Figure 5 for various values of surface radiation parameter, R, against  It is observed that both velocity and temperature tends to increase when surface radiation parameter is intensified. It is expected since R adds more heat near the vicinity of the plate which allows the fluid to move faster and as a result both temperature and velocity of the fluid increases within the boundary layer region. The reason for this behavior is discussed in the earlier discussion. In addition, it is also inspected that thermal and momentum boundary layer thicknesses slightly increases as well due to the increment in surface radiation parameter, R.
It is observed that both velocity and temperature tends to increase when surface radiation parameter is intensified. It is expected since R adds more heat near the vicinity of the plate which allows the fluid to move faster and as a result both temperature and velocity of the fluid increases within the boundary layer region. The reason for this behavior is discussed in the earlier discussion. In addition, it is also inspected that thermal and momentum boundary layer thicknesses slightly increases as well due to the increment in surface radiation parameter, R.
5.3. Effect of R and Ri* on Heatlines
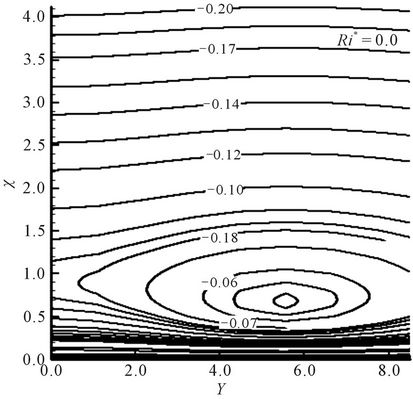
Here heatlines are drawn in Figures 6-7 for different values of physically important parameters R and Ri*. It should be noted that in both figures Pr is taken to be 0.05 which is appropriate for liquid metals.
In Figure 6 the influence of modified Richardson number, Ri* = 0.0, 2.0 and 5.0 is expressed on heatlines so that one can visualize the phenomena of rate of heat transfer. In this case surface radiation parameter assumes the value 0.1. It is observed from the figure that the process of heat transfer get stronger as modified Richardson number increases from 0.0 to 5.0. Therefore, Ri* serves to sustain the strength of the fluid flow and ultimately rate of heat transfer increases within the boundary layer.
Lastly, in Figure 7 attention has been given to observe the behavior of heatlines for several values of surface radiation parameter, R which is equal to 0.0, 0.25 and 0.5. The numerical results for the specified values of R are plotted against Y while χ varies between 0.0 to 4.0 and Ri* is chosen as 20.0. From the Figures 7(a)-(c), it is inferred that heat transfer diminishes as surface radiation parameter is intensified.
6. Conclusions
In the present article, the effect of thermal radiation on mixed convection flow along a semi-infinite vertical surface is analyzed in the nonabsorbing medium. The vertical plate is located in the optically transparent medium and particularly the processes of radiation absorption, emission and scattering are neglected. The relationship between convection and thermal radiation is however established with the aid of second kind of boundary condition on the thermally radiating vertical surface. In this problem consideration has been given to those working fluids which act as liquid metals by taking Pr = 0.05 which is appropriate for lithium. The governing equations are obtained for the regimes where modified Richardson number, Ri*, is termed as small (i.e. when Ri*  1), sufficiently large (i.e. when Ri*
1), sufficiently large (i.e. when Ri*  1) and also in the regime where Ri* covers all values from 0 to ∞. The corresponding governing equations for each regime are reduced to parabolic partial differential equations using PVF which are then integrated numerically by employing an efficient implicit finite difference method in connection with Gaussian elimination technique. The numerical results are acquired in terms of local skin friction coefficient,
1) and also in the regime where Ri* covers all values from 0 to ∞. The corresponding governing equations for each regime are reduced to parabolic partial differential equations using PVF which are then integrated numerically by employing an efficient implicit finite difference method in connection with Gaussian elimination technique. The numerical results are acquired in terms of local skin friction coefficient,  , and local Nusselt number coefficient,
, and local Nusselt number coefficient, 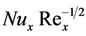 , for different values of the parameters, such as, surface radiation parameter, R, modified Richardson number, Ri*, and locally varying parameter, χ, for fluids
, for different values of the parameters, such as, surface radiation parameter, R, modified Richardson number, Ri*, and locally varying parameter, χ, for fluids
 (a)
(a)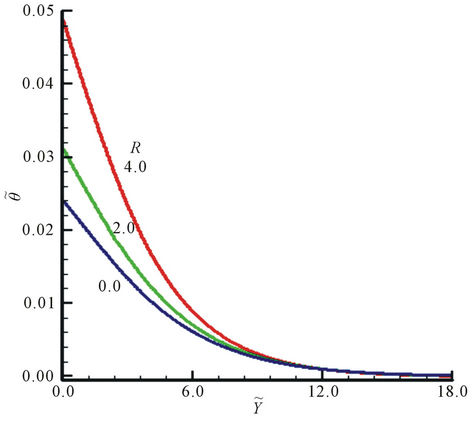 (b)
(b)
Figure 5. (a) Velocity and (b) temperature profiles with  for R = 0.0, 2.0, 4.0 while Ri* = 30.0, Pr = 0.05.
for R = 0.0, 2.0, 4.0 while Ri* = 30.0, Pr = 0.05.
 (a)
(a) (b)
(b) (c)
(c)
Figure 6. Heatlines for (a) Ri* = 0.0, (b) Ri* = 2.0, (c) Ri* = 5.0 while Pr = 0.05 and R = 0.1.
 (a)
(a) (b)
(b) (c)
(c)
Figure 7. Heatlines for (a) R = 0.0, (b) R = 0.25, (c) R = 0.5 while Pr = 0.05 and Ri* = 20.0.
having Pr = 0.05. From the above investigation we may conclude that 1) coefficient of local skin friction and coefficient of local Nusselt number diminishes owing to the increase in the surface radiation parameter, R; 2) both coefficient of local skin friction and coefficient of local Nusselt number enhances significantly owing to the increase in the locally varying parameter, χ; 3) increment in the modified Richardson number is responsible for uprising the wall shear stress of the fluid while on the other hand rate of heat transfer decreases.