1. Introduction
This article shows that the multiplicity of rational beliefs concerning the value of money decides whether money is neutral under perfect information structure in the twoperiod OLG model. The result is kept intact even if new money injected into the economy is subject to the model of Lucas [1]. This result contrasts with Otani [2] and Otaki [3-5].
Even if the nominal rate of interest on money increases (i.e., money supply increases), people can consistently believe that the purchasing power of money (the inverse of the next period price level) is retained.1 Then the real interest rate becomes higher, and thereby matching the supply, and the demand for money increases.
From assumptions concerning the utility function, this situation also implies the reduction of current consumption and leisure. Thus, the monetary expansion increases current total output, and hence, money becomes nonneutral.
We must note that the attained equilibrium is stationary in the sense that values of real endogenous variables such as current/future consumption and leisure are entirely time-independent. This assertion holds, since once the real interest rate is heightened by an increase of the nominal interest rate (increment of nominal money supply per capita), one may expect that the change in the inflation rate will equal that of the nominal interest rate; the heightend real interest rate is kept intact, and thus, the equilibrium becomes self-enforcing and stationary.
The rest of paper is organaized as follows. In Section 2, we construct the same model as Lucas [1], except for the formation of rational expectation concerning the value of money, and proves the non-neutrality of money. A welfare economics implication is also analyzed. Section 3 contains brief concluding remarks.
2. The Model
2.1. The Structure of the Model
We use essentially the same model as Lucas [1], excluding uncertainty. In every period a unit individual is born and lives two periods. Each individual has an indentical utility function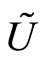 :
:
 (1)
(1)
where  and
and  are the current and future consumption level, and
are the current and future consumption level, and  denotes the hours worked per individual.
denotes the hours worked per individual.
Furthermore, 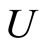 and
and  satisfy the following properties:
satisfy the following properties:
 (2)
(2)
 (3)
(3)
 (4)
(4)
 (5)
(5)
2.2. The Maximization Problem of Representative Individual
Each individual maximizes his/her lifetime utility  subject to the following budget constraint:
subject to the following budget constraint:

 (6)
(6)
 (7)
(7)
where  denotes the increment of money supply per capita.
denotes the increment of money supply per capita.  is the inverse of the real interest rate.
is the inverse of the real interest rate.
The Kuhn-Tucker condition implies that the optimal decision  satisfies
satisfies
 (8)
(8)
 , (9)
, (9)
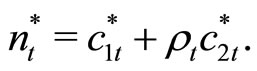 (10)
(10)
2.3. Market Equilibrium
There are two markets in the above model: the money market and good market. By Walras’ law, we can neglect the equilibrium condition for the good market. The money market equilibrium condition is
 (11)
(11)
Instead of the quatity-theoretic equilibrium price function imposed by Lucas [1], let us assume that money is credible in the sense of Otaki [5]—That is, the rational expectation concerning the current purchasing power of money  is not purturbed by an increse of
is not purturbed by an increse of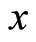 :
:
 (12)
(12)
The general equilibrium of markets is attained by five equations: (8), (9), (10), (11), and (12). Endogenous variables are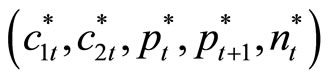 .
.
The partial equilibrium of labor  and the younggeneration’s consumption
and the younggeneration’s consumption  is illustrated by Figure 1. The downward sloping curve
is illustrated by Figure 1. The downward sloping curve 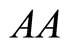 is the locus of Equation (8), which is easily derived from Assumption (3).
is the locus of Equation (8), which is easily derived from Assumption (3).
The upward sloping curve  is the locus of Equation (10), which is combined with Equation (9). The procedure is as follows: Substituting Equation (9) into (10), we obtain
is the locus of Equation (10), which is combined with Equation (9). The procedure is as follows: Substituting Equation (9) into (10), we obtain

Differentiating both sides of the above equation,

 (13)
(13)
 (14)
(14)
holds. Hence Curve  is upward sloping for any fixed
is upward sloping for any fixed . When the money market equibrates, the equilibrium consumption of younger generation and output is determined at the intersection of Curves
. When the money market equibrates, the equilibrium consumption of younger generation and output is determined at the intersection of Curves  and
and  (Point
(Point ).
).
Whenever money is credible, it is facile to depict the property of money market equilibrium. From Equations (11) and (12), we obtain
 (15)
(15)
Since  is an increasing function of
is an increasing function of  from Assumption (4), Equations (14) and (15) imply that Curve
from Assumption (4), Equations (14) and (15) imply that Curve 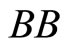 shifts toward the south-east, like Curve
shifts toward the south-east, like Curve , by an increase of
, by an increase of . Thus, the economy moves from Point
. Thus, the economy moves from Point  to
to .
.
Accordingly, as long as money is credible, a monetary
expansion increases the output  and future consumption
and future consumption , and decreses the younger-generation’s consumption
, and decreses the younger-generation’s consumption . To sum up:
. To sum up:
Theorem 1. If money is a credible asset, it becomes non-neutral to the real economy. An accelaration of monetary growth hightens the real interest of money, and hence, stimulates future consumption and output/labor supply, economizes current consumption.
Next we shall show that the equilibrium above depicted is a stationary rational expectation equilibrium. Suppose that the economy is located at Point  by an increase of
by an increase of , and individuals believe that the higher equilibrium real interest rate
, and individuals believe that the higher equilibrium real interest rate  prevails thereafter.
prevails thereafter.
Then by the definition of  (Equation (7)),
(Equation (7)),
 (16)
(16)
holds. That is, individuals consider that the change in the equilibrium inflation rate is equal the acceleration rate of monetary growth because there is no substantial change in the economic environment after period . Since
. Since  and
and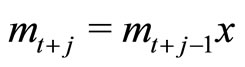 ,
,
 (17)
(17)
also holds. Combining Equation (17) with (16), we finally obtain
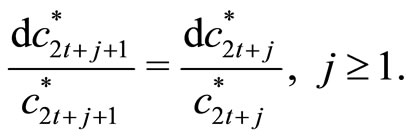 (18)
(18)
Thus, the equilibrium consumption of an old individual  is time-independent.
is time-independent.
It is clear from Equations (8) and (14) that the rest of the two endogenous variables  are also timeindependent. Consequently, the equilibrium illustrated by Point
are also timeindependent. Consequently, the equilibrium illustrated by Point  is stationary in the sense that every equilibrium value of endgenous variables is time-independent. One can thus affirm Theorem 2. The rational expectation equilibrium defined by Equations (8)-(10), (12), and (16) is stationary (i.e., time-independent). Hence the heightned real interest rate caused by an increase of the nominal interest on money
is stationary in the sense that every equilibrium value of endgenous variables is time-independent. One can thus affirm Theorem 2. The rational expectation equilibrium defined by Equations (8)-(10), (12), and (16) is stationary (i.e., time-independent). Hence the heightned real interest rate caused by an increase of the nominal interest on money  permanently affects the real variables.
permanently affects the real variables.
2.4. A Welfare Implication of the Model
By Theorem 1, a monetary expansion (an increase in ) stimulates the equilibrium real GDP
) stimulates the equilibrium real GDP  through the rise of the real rate of interest. We here consider its welfare economics implication. Let the Lagrangean of individual decision
through the rise of the real rate of interest. We here consider its welfare economics implication. Let the Lagrangean of individual decision  that is evaluated at the equilibrium value.
that is evaluated at the equilibrium value.
Then, using the envelop theorem, we obtain
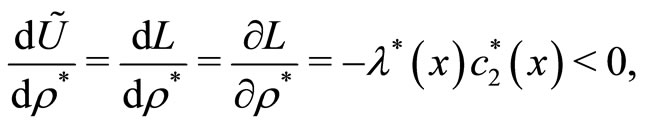
where  is the Lagrangean multiplier. Accordingly, a monetary expansion improves the economic welfare since it makes future goods cheaper.
is the Lagrangean multiplier. Accordingly, a monetary expansion improves the economic welfare since it makes future goods cheaper.
3. Concluding Remarks
This paper shows that money is non-neutral as long as it is credible even if we obey the money-supply rule proposed by Lucas [1]. A monetary expansion (an accelaration of the money growth rate) surely hightens the real rate of interest of money whenever people believe that money is credible. The effect of intertempral substitution leads them to work more to prepare for more future consumption, and thus, the aggregate products increases. It also implies that the economic welfare is improved by a monetary expansion.
NOTES