On the Consistency of the First-Order-Approach to Principal-Agent Problems ()
1. Introduction
The principal-agent model under moral hazard represents a cornerstone in the analysis of contractual arrangements intended to achieve mutual gains between agents with asymmetric knowledge; see [3-8], and others. This model pursues the characterization of the second-best contract, i.e., a rule which establishes how to share the output between the employer (principal) and the employee (agent) in order to extract from the last one the optimal amount of an unobservable input. The importance of the agency relationship in economic activities makes the model relevant from a theoretical point of view because it provides a conceptual framework to analyze actual incentives in terms of efficiency. Furthermore, it makes it possible to perform exercises of comparative statics on the model parameters (in order to determine, for example, the effect of uncertainty on performance and welfare).
However, a satisfactory mathematical characterization of the solution to the principal-agent model involves serious technical difficulties, which has prevented the development of simple solutions to the problem. In Haubrich’s words: “Unfortunately, most versions [of the principal-agent model] have intractable solutions. Quantitative solutions do not readily emerge from the implicit equations that define the sharing rules, especially in models with a continuum of states” (see [9], p. 259).
An important solution to the problem of determining optimal contracts in realistic agency setups is based on the so-called first-order approach (FOA henceforth). The simplification introduced by the FOA is important because it makes it feasible to characterize optimal incentive contracts ([8,10-15], et al.). We center our attention on analyzing the consistency of the solution provided by the FOA.
Technically, the FOA consists in replacing the incentive compatibility constraint of the optimization problem by its first-order condition. This procedure has a long history in the incentives literature, but its validity must not be taken for granted. James Mirrlees was the first who observed that substituting the correct constraint by its first-order condition may lead to wrong solutions (see [3]). In particular he showed that, in some circumstances, the informational unconstrained solution can be arbitrarily approximated, so local maxima will not coincide with global ones. That is, when the unconstrained solution to the problem can be arbitrarily approximated by means of a Mirrlees forcing contract, the FOA fails because global maxima cannot be found within the set of stationary points. The counterexample provided by Mirrlees against the validity of the FOA, rather than a solution to the problem, has been considered a pathological situation to be avoided in more elaborated and realistic models.
In order to avoid this problem, [1,2,5] among others attempted to provide sufficient conditions validating the FOA. Many papers on managerial retribution and agency relationships appeal to the FOA in their analysis of incentive contracts (see references above). Many others appeal to the FOA in contexts where it is well known that it cannot be invoked (e.g., [16,17]).
Although the FOA is a successful shortcut often used in theoretical work, we show that the proposed solutions can lead to inconsistencies that make them invalid from a theoretical point of view. In particular, we show that some solutions contradict basic economic assumptions (e.g., that marginal utility must be positive). Once the inconsistencies are detected, it is possible to interpret the correct solutions to the problem as actual solutions to moral hazard problems implemented in practice, in particular, non-linear incentives and minimum payments.
The use of non-linear contracts is a common practice in executive compensation. Stock options, bonus contracts or contracts based on performance-standards are paramount examples of non-linear contracts used in firms. However, in spite of the undeniable success that such contracts have in managerial compensation, a fully satisfactory explanation for their use in terms of efficiency in effort-extraction and risk-sharing still remains as a theoretical challenge. In Prendergast words, “the theoretical literature has made little progress in understanding the observed (nonlinear) shape of compensation contracts, despite costs associated with nonlinearities” ([18], p. 15). This paper provides a rationale for the use of non-linear incentives. For example, those including a lower bound in compensation. In [8] it is suggested that some bounds may be necessary in incentives design in order to account for the agent’s and principal’s wealth constraints. In [19] the question is analyzed in detail. We instead justify the appearance of lower bounds endogenously, and piecewise-linear contracts implemented in practice can be seen as approximations to second-best contracts with bounds.
Section 2 introduces the mathematical model and its solution when the FOA is applied. Section 3 presents a number of inconsistencies the approach can yield when conditions “validating” the FOA are met. In Section 4, we justify the use of non-linear contracts and minimum payments in principal-agent relationships. Section 5 concludes.
2. Mathematical Specification
The setup is the principal-agent model in the formulation due to [8] in an extension of [4]: a risk-neutral principal (she) employs a risk-averse and effort-averse agent (he) to carry out an unobservable task that influences an ex post signal x (which we identify with output); the agent receives a payment s(x) for his job. The optimization program is stated as follows:
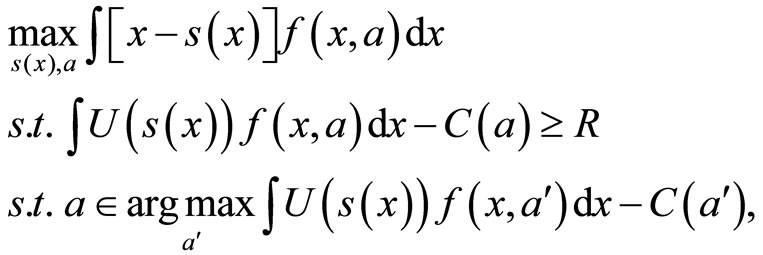 (P1)
(P1)
where U(·) represents the (standard) utility function of the agent; R represents the agent’s reservation utility; C(a) represents the agent’s cost of providing a level of effort a, with  > 0 and
> 0 and  > 0; and f(x,a) represents the output density function for a given level of effort. The two constraints in (P1) are respectively known as the participation constraint and the incentive compatibility constraint. In [20, pp. 51-55] the reader can find a pedagogical presentation of the principal-agent model.
> 0; and f(x,a) represents the output density function for a given level of effort. The two constraints in (P1) are respectively known as the participation constraint and the incentive compatibility constraint. In [20, pp. 51-55] the reader can find a pedagogical presentation of the principal-agent model.
The optimization program (P1) is difficult to solve, and few general results can be obtained if additional specific assumptions are not made. A shortcut often used is to replace the incentive compatibility constraint by its first-order condition, i.e., the original constraint

is replaced by the relaxed constraint
 where
where . This procedure is known as the firstorder approach (FOA). The economic literature provides sets of conditions under which the FOA holds. The importance of this simplification is that makes it feasible the characterization of optimal contracts. In [21, p. 253], an intuitive argument justifying the FOA is presented.
. This procedure is known as the firstorder approach (FOA). The economic literature provides sets of conditions under which the FOA holds. The importance of this simplification is that makes it feasible the characterization of optimal contracts. In [21, p. 253], an intuitive argument justifying the FOA is presented.
Let us review the sets conditions intended to validate the FOA. The Mirrlees-Rogerson conditions establishes that if the density f satisfies the Monotone Likelihood Ratio Property (i.e.,  is non-decreasing), and the distribution function
is non-decreasing), and the distribution function  satisfies the Convex Distribution Function condition (CDFC, which mathematically means that
satisfies the Convex Distribution Function condition (CDFC, which mathematically means that ), then the first-order approach is valid.1 It has been argued that this set of conditions is not very useful from a practical point of view, because it is not easy to find distributions satisfying the CDFC. In order to avoid this drawback, [22] provides two rich families of examples satisfying the Mirrlees-Rogerson conditions.
), then the first-order approach is valid.1 It has been argued that this set of conditions is not very useful from a practical point of view, because it is not easy to find distributions satisfying the CDFC. In order to avoid this drawback, [22] provides two rich families of examples satisfying the Mirrlees-Rogerson conditions.
[2] provides a second set of conditions, less stringent than the Mirrlees-Rogerson one. In particular, [2] shows that if the density function can be expressed as 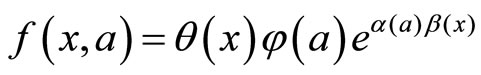 with b(x) concave,
with b(x) concave,  is concave, expected output is concave in effort, and
is concave, expected output is concave in effort, and  is concave for z > 0, then the FOA holds (see [2], Cor. 1). He also provides a more relaxed set of conditions (see [2], Th. 1).
is concave for z > 0, then the FOA holds (see [2], Cor. 1). He also provides a more relaxed set of conditions (see [2], Th. 1).
[21] discusses the results in [1,2], generalizing and comparing them in the multisignal case.
When the first-order approach can be invoked, the optimal sharing rule s*(x) satisfies the two following conditions (see [8] or [2]):
 (1a)
(1a)
 (1b)
(1b)
where  and
and  represent the Lagrange multipliers associated to the participation constraint and the incentive compatibility constraint respectively. The optimal contract can thus be derived from (1a) as a function of
represent the Lagrange multipliers associated to the participation constraint and the incentive compatibility constraint respectively. The optimal contract can thus be derived from (1a) as a function of ,
,  and a*, which are obtained from the two constraints in (P1) together with (1b). Thus, the principal can design a contract that extracts the (second-best) level of effort from the agent.
and a*, which are obtained from the two constraints in (P1) together with (1b). Thus, the principal can design a contract that extracts the (second-best) level of effort from the agent.
However, the papers devoted to justify the FOA are centered on showing that the agent’s utility is concave in effort, ignoring that in some cases the existence of the two (positive) multipliers may not be guaranteed. Let us analyze this question in detail.
3. Consistency of the Solution
This section shows that the contract defined by Equation (1a) can lead to situations where the FOA does not hold even when the Mirrlees-Rogerson or Jewitt’s conditions hold. In particular, situations where the existence of the Lagrange multipliers implies that the agent’s marginal utility is negative for low outcomes.
First, let us see what happens when the likelihood ratio  is a non-decreasing and unbounded-from-below function of output. Unbounded-from-below likelihood ratios have been considered in [4, p.125], and ruled out in [19, ft.2]. However, none of them mention that when
is a non-decreasing and unbounded-from-below function of output. Unbounded-from-below likelihood ratios have been considered in [4, p.125], and ruled out in [19, ft.2]. However, none of them mention that when  is not bounded-from-below, the solution provided by the FOA is not admissible. The reason is that multipliers
is not bounded-from-below, the solution provided by the FOA is not admissible. The reason is that multipliers  and
and  have constant values, so they must be independent of realized output. Given that
have constant values, so they must be independent of realized output. Given that  is positive when the FOA holds (see [2, Lemma 1]), if the likelihood ratio is unbounded from below, for any pair of multipliers there exist low values of x such that
is positive when the FOA holds (see [2, Lemma 1]), if the likelihood ratio is unbounded from below, for any pair of multipliers there exist low values of x such that  becomes negative. Then Equation (1a) can not be satisfied because marginal utility must be positive all along the output range. Consequently, the likelihood ratio must be bounded from below.
becomes negative. Then Equation (1a) can not be satisfied because marginal utility must be positive all along the output range. Consequently, the likelihood ratio must be bounded from below.
However, neither the Mirrlees-Rogerson nor the Jewitt sets of sufficient conditions guarantee such a requirement. A counterexample to Jewitt’s “sufficiency” can be found in his own paper (see [2], example c, p. 1183). The example provided by [1] (footnote 4) also has an unbounded-from-below likelihood ratio. As Rogerson restricts output to take values in a discrete and bounded set, the likelihood ratio is not unbounded in his example. However, the continuous version of Rogerson’s conditions can lead to unbounded-from-below likelihood ratios.
[22] provides two families of examples (both continuous) satisfying the Mirrlees-Rogerson conditions, but as has been shown, such requirements do not guarantee that the likelihood ratio is well-behaved. In fact, in both families of examples it is easy to impose certain requirements under which likelihood ratios are unbounded.
An example that satisfies both sets of conditions with an unbounded likelihood ratio corresponds to the case where output has a density function equal to

and where the agent influences the parameter p with his actions in such a way that p = a + 2.
Furthermore, if the agent’s utility function is unbounded-from-below, a Mirrlees forcing contract can be constructed; see [3]. However, it is worth observing that this kind of forcing contracts, which produces an arbitrary approximation to the first-best solution, can only arise when the FOA does not work (because the FOA does not provide well-defined contracts when 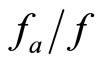 is unbounded from below). Then, there is a more fundamental argument invalidating the FOA than the appearance of Mirrlees forcing contract because, contrary to [3], an unbounded utility function is not required.
is unbounded from below). Then, there is a more fundamental argument invalidating the FOA than the appearance of Mirrlees forcing contract because, contrary to [3], an unbounded utility function is not required.
More important and of greater concern is the case where likelihood ratios are bounded-from-below. Next, we show that, even when  is bounded from below, expression
is bounded from below, expression  can be negative if output is low enough, which implies that FOA does not produce a satisfactory candidate for a second-best contract. Consider a principal-agent setting where output has a gamma distribution with parameters p and a, where p is an integer and a is a positive number. The density function is:
can be negative if output is low enough, which implies that FOA does not produce a satisfactory candidate for a second-best contract. Consider a principal-agent setting where output has a gamma distribution with parameters p and a, where p is an integer and a is a positive number. The density function is:
 . (3)
. (3)
The expected output is pa; the output variance is . The likelihood ratio is linear in output:
. The likelihood ratio is linear in output:
 .
.
This model has been often used in the incentives literature: in the seminal article [8] it is used with illustrative purposes. [11] discusses the advantages of replacing curvilinear second-best bonus plans by their piecewise linear approximations (quota-based sales compensation schemes). [12] analyzes the advantages of introducing stock options in managerial incentives.
Assuming that the agent has a cost of effort equal to , the multipliers are:
, the multipliers are:
 ,
, .
.
If the agent’s reservation utility R is set equal to zero (for example because the market for executives’ services is competitive), simple calculations yield:
 which is negative if output x is sufficiently low. It must be mentioned that
which is negative if output x is sufficiently low. It must be mentioned that  can also be negative when the reservation utility R is strictly positive.2 Then, none of the two examples provided by Jewitt with continuous output is in general valid (see [2], p. 1183, examples (a) and (c)).
can also be negative when the reservation utility R is strictly positive.2 Then, none of the two examples provided by Jewitt with continuous output is in general valid (see [2], p. 1183, examples (a) and (c)).
4. Minimum Payments and Kinked Incentives
In this section we link the inconsistencies that can appear when the FOA is invoked to actual incentives used in practice. In particular, we suggest that solving correctly the optimization program P1 provides a rationale for the use of non-linear and option-like incentives, which represents a popular practice today (stock-options, bonus based on performance standards, and others), and a theoretical foundation for the existence of minimum payments in executive compensation, as [13,14] suggest. The following result formalizes the argument:
Proposition: Assume that the agent’s utility function is concave in effort. If no positive multipliers can be found ensuring that Equation (1a) holds for the entire output range, the solution to P1 will include a minimum wage.
Proof: Consider first that the likelihood ratio is unbounded from below.
As  must be non-negative, the agent’s fee can not be below
must be non-negative, the agent’s fee can not be below , which becomes the minimum wage (whenever finite).3
, which becomes the minimum wage (whenever finite).3
(An alternative reasoning can be taken from [4, p. 125, Equations (69)-(71)]: if s(x) admits a minimum wage, the maximization of the Lagrangean (L) with respect to s(x) in order to obtain Equation (1a) leads to:
 .
.
If , then
, then ; for those output values that correspond to
; for those output values that correspond to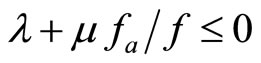 , s(x) must be equal to the minimum wage.)
, s(x) must be equal to the minimum wage.)
When the likelihood ratio is bounded from below, we have shown that  can also be negative for low enough outputs. The argument given for the existence of a minimum wage in the unbounded case keeps working in the bounded case, and the correct solution to program P1 will contain a corner.□
can also be negative for low enough outputs. The argument given for the existence of a minimum wage in the unbounded case keeps working in the bounded case, and the correct solution to program P1 will contain a corner.□
The unbounded case has been considered in [4,19]. [19] rules it out in order to avoid Mirrlees forcing contracts, while [4] uses it to justify the existence of minimum payments. Our interpretation is that when effort is highly productive for very low outcomes (i.e., the likelihood ratio is unbounded from below), the optimal fee has a minimum value, which induces a kinked point in the incentive system if salaries are positive and the minimum wage is above zero.
The bounded case is more worrying, and the conclusions on it are novel, underlining that the underlying problem in the unbounded case is deeper than it seems at first sight. From the discussion in Section 3, we conjecture that non-linear salaries are more likely to be observed in moral hazard environments where agents have low outside opportunities. For example, if executives offer their services in a competitive market.
Finally, it is worth mentioning that [19] also justifies the appearance of option-like incentives when minimum wages are imposed. However, [19] imposes minimum payments exogenously, while we have endogenously justified the existence of such lower bounds on fees. [13] also mentions that kinked non-linearities may appear in incentives when a minimum wage is binding, something implicit in Holmstrom’s seminal work (the contract solution is restricted to lie in the closed domain [c, d + x] ). [13] appeals to the manager’s limited liability in order to justify such a minimum fee, which is unnecessary in our context. They argue that stock options can be a better alternative than shares in creating incentives for CEOs, but their argument is not centered on the appearance of corners in incentives. On the other hand, and in answer to their claim that “the power class utility functions provides additional motivation for the requirement of limited liability in the contract”, we point out that  must be positive, so no problem involving power utilities can arise.
must be positive, so no problem involving power utilities can arise.
5. Conclusions
The widespread use of incentives under moral hazard makes it important the characterization of second-best contracts. This paper analyzes the consistency of the solutions obtained appealing to the first-order approach.
We have shown that, in some contexts, the solutions are devoid of economic sense, because they lead to situations compatible with negative marginal utility. This can happen both with bounded and unbounded likelihood ratios. Then, although the first-order approach is a powerful and elegant tool, it is crucial to check whether the contracts obtained are well-defined indeed.
Once analyzed the consistency of the approach, we interpret the correct solutions to the agency problem as salaries containing non-linearities, which represent actual arrangements implemented in practice.
We obtain that if the likelihood ratio is unbounded from below (i.e., agent’s effort is extremely productive for low outputs), a minimum payment must be imposed. If the likelihood ratio is bounded-from-below, corners can also arise in optimal contracts; in this case, we conjecture that kinked incentives are more likely to be used when agents have low outside opportunities.
We thus offer a rationale for the existence of minimum wages and kinked contracts without departing from a canonical principal-agent framework, nor imposing additional constraints on agents’ wealth.
NOTES
2To see this, take into account that: 1)  (see [2]); 2)
(see [2]); 2)  is negative for low outputs (and positive for large ones) because
is negative for low outputs (and positive for large ones) because  and
and  increases with output. Then,
increases with output. Then,  will be negative if output is low (unless multiplier
will be negative if output is low (unless multiplier  is sufficiently large). If
is sufficiently large). If  is small (for example because the reservation utility R is small), then
is small (for example because the reservation utility R is small), then  is negative for small outputs.
is negative for small outputs.
3Holmstrom restricts s(x) to lie in [c, d + x], which can be justified because agent’s and principal’s wealth put bounds on s(x). In our context, c is naturally given by  as long as it remains finite. For example, if
as long as it remains finite. For example, if ,
,  and
and . Observe that in this case both the agent’s utility and the likelihood ratio are both unbounded from below functions, so a Mirrlees forcing contract can be constructed.
. Observe that in this case both the agent’s utility and the likelihood ratio are both unbounded from below functions, so a Mirrlees forcing contract can be constructed.