Implications of an Aging Population on Pension Systems and Financial Markets ()
1. Introduction
How can pension schemes be sustainably financed? This is an important issue particularly with regard to the demographic changes in many industrialized countries but also in other emerging economies such as China and India. While the immediate concern is the financial market and currency crisis, the much more important challenge for capital markets over the medium and long-term is dealing with the implications of an aging population on pension systems and the role that financial markets can play in providing adequate private pensions.
Demographic changes are the result of steadily increasing life expectancy due to medical improvements and falling fertility rates1. The hump-shaped profile of fertility rates has created the “baby-boom” generation; that is, a generation or cohorts which are larger than the preceding and subsequent cohorts. Therefore, the effects of the baby-boom generation are only temporary as this generation born during the high fertility years pass away. On the other hand, the impacts of increasing life expectancy are of a more permanent nature. The implication of an aging population is an increasing ratio of people in retirement age compared to the working age population. The retirement of the baby boom generation will increase this share as those cohorts retiring will be followed by smaller cohorts. Analogously, improvements in life expectancy directly cause an increase of people in retirement at any given time. Due to the increased ratio of people in retirement relative to people of working age there are serious financial problems for pay-as-you-go financed pensions (mostly public pensions) as well as to funded pensions (generally private pensions).2 Public pension schemes would see the number of young working people contributing dwindle relative to older retirees withdrawing benefits. This would cause increasing public expenditures on pensions. Additionally, many public pension systems are designed in the manner which creates incentives for early retirement and worsens the impacts of demographic changes on public pension expenditures (see e.g. Duval [4]). The aging population has, however, also negative effects on a capital funded pension system since the capital market return will drop due to the demographic change. This result can be explained by two effects:
• The capital intensity increases since the capital funded pension schemes initiate a higher capital accumulation in the whole economy. At the same time, the number of people in the workforce diminishes due to demographic changes. This leads to a price increase for the factor workforce and to a price decrease for the factor capital. The capital market return will consequently fall.
• A second argument is a predicted collapse of prices on the capital markets. Due to the many retired sellers and the low number of young buyers, the prices of the assets (shares, bonds, real estate etc.) must fall.
In this article, we introduce firstly a macroeconomic model of overlapping generations in which we can analyze the effects of the demographic changes on pension schemes as well as the interactions between pension systems on the one hand and capital markets on the other hand. The model consists of three building blocks:
• A population model which describes the presumptions with respect to population development.
• Modeling of enterprises in view of the dependence between the existing pension system and the real eco nomic variables such as wage and capital stock and
• Description of risks on financial markets as well as the interactions between pension systems and stock prices or interest rates.
Furthermore, we will examine the effects of pension systems on welfare distribution and consumption as well as the rate of saving within generations.
2. The Model
2.1. Population Model
To facilitate the modeling, the model uses discrete time steps . The population consists of
. The population consists of  generations. All consumers live for exactly
generations. All consumers live for exactly  time steps (overlapping generations model) and exhibit a homogeneous savings and consumption behavior within one generation. Such a model is particularly suited to describe the financial interactions between the generations. Each generation is identified in each period by an index
time steps (overlapping generations model) and exhibit a homogeneous savings and consumption behavior within one generation. Such a model is particularly suited to describe the financial interactions between the generations. Each generation is identified in each period by an index  that describes the remaining life expectancy. Consequently,
that describes the remaining life expectancy. Consequently,  is the youngest generation to be born at the beginning of the considered period,
is the youngest generation to be born at the beginning of the considered period,  represents the oldest generation that dies at the end of the period. The entire population is thus represented by a vector
represents the oldest generation that dies at the end of the period. The entire population is thus represented by a vector , where
, where  is the number of consumers in generation
is the number of consumers in generation  at the time
at the time . The time evolution of the population is described by the birth rate
. The time evolution of the population is described by the birth rate  with:
with:
 (1)
(1)
 (2)
(2)
Equation (1) describes the aging of the overlapping generations, Equation (2) describes the birth rate as a function , depending on the population structure in the period before. In the case of a constant population we find:
, depending on the population structure in the period before. In the case of a constant population we find:
 (3)
(3)
For the numerical simulations in later sections of this work, the demographic change of the population is described by the following model (see Hillebrand [5]). Here the population is modeled by age-dependent birth rates :
:
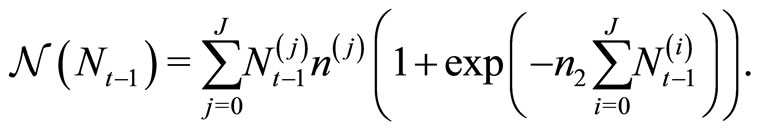 (4)
(4)
Using  we have constant growth rates and thus an exponential population change. For
we have constant growth rates and thus an exponential population change. For  the birth rates decrease as a function of the total population
the birth rates decrease as a function of the total population
 . With the birth rates added up over all generations
. With the birth rates added up over all generations  the asymptotic stationary value is obtained
the asymptotic stationary value is obtained
 (5)
(5)
so that the population tends to the constant distribution
 .
.
Furthermore, the model of overlapping generations contains a retirement threshold  for the consumers. It is assumed that each member of the working
for the consumers. It is assumed that each member of the working  provides
provides  units of labor to the workforce market. The total labor supply of the economy
units of labor to the workforce market. The total labor supply of the economy  is given by:
is given by:
 (6)
(6)
For simplicity it is assumed that taxes do not exist in the model. A share  of gross wages has to be paid in a pay-as-you-go system, so that each worker with the gross wage per unit of work
of gross wages has to be paid in a pay-as-you-go system, so that each worker with the gross wage per unit of work  gets the net wage:
gets the net wage:
 (7)
(7)
The pension income is composed of the product of the contribution rate and the total income from work activeties, divided by the number of pensioners:
 (8)
(8)
All individuals can consume their current wealth in a period or transfer it to the next period by two investment opportunities. Using these two alternatives, there is also the possibility to provide for the retirement phase. On the one hand, there is a corporate bond with a maturity of one period available. This may be traded at time  at unit price and attains in the next period
at unit price and attains in the next period  one from the company’s success dependent return
one from the company’s success dependent return . As
. As  is determined at time
is determined at time , the bond is a risk-free opportunity to transfer wealth to the next period. As an alternative, an investment in shares is possible. The shares are traded on the rates
, the bond is a risk-free opportunity to transfer wealth to the next period. As an alternative, an investment in shares is possible. The shares are traded on the rates 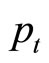 and deliver in each period a stochastic dividend
and deliver in each period a stochastic dividend . In the model short-selling of bonds is possible (“credit”), whereas for shares this is not possible. The portfolio of a consumer
. In the model short-selling of bonds is possible (“credit”), whereas for shares this is not possible. The portfolio of a consumer  is described by
is described by
 . Here
. Here  is the number of bonds and
is the number of bonds and  is the number of owned shares.
is the number of owned shares.
The wealth  of a consumer is given as the sum of wage or pension income and the income from capital investment decisions
of a consumer is given as the sum of wage or pension income and the income from capital investment decisions  of the previous period
of the previous period
 (9)
(9)
It is assumed that all individuals are selfish and do not pass on an inheritance. This implies that consumers in their last period of life sell all shares and do not buy bonds.
2.2. Consumer Behavior
This section describes the decision-making process, which part of their wealth the individuals use for consumption and how they invest the rest in bonds or shares. The goal of the individual here is to maximize their wealth within a planning horizon.
The decisions are influenced by expectations of the consumers regarding their future wage or pension income
 and the expected bond yield
and the expected bond yield
 within the planning horizon of
within the planning horizon of 
periods. In addition, the decisions are influenced by the uncertainty regarding the impact of unforeseen developments of stock prices and dividends. For the consumer different strategies for consumption , bond investment
, bond investment  and share investment
and share investment  are available. Within the planning horizon a strategy has to fulfill the following conditions in each period:
are available. Within the planning horizon a strategy has to fulfill the following conditions in each period:
 (10)
(10)
 (11)
(11)
This must be met for all possible (random) stock prices  and dividend payments
and dividend payments . The existence of such a strategy under certain constraints, which will not be dealt with here, is mathematically proven (see Hillebrand [5], pp. 15). The goal of a consumer is to maximize the logarithmic utility function that reaches to the end of his life:
. The existence of such a strategy under certain constraints, which will not be dealt with here, is mathematically proven (see Hillebrand [5], pp. 15). The goal of a consumer is to maximize the logarithmic utility function that reaches to the end of his life:
 (12)
(12)
The discount rate  represents the general fact that individuals prefer consumption in the presence compared to consumption in the future.
represents the general fact that individuals prefer consumption in the presence compared to consumption in the future.
It has been found that it is not necessary to consider the entire planning horizon in the model (see Hillebrand [5], p. 20). The decision problem can be traced back to a single-stage problem, so that demand functions are specified which describe the optimized consumer demand for one period. The derivation of the formula models the uncertainty of the stock market using a probability distribution  for the sum
for the sum  of share price and dividend. The expectation value
of share price and dividend. The expectation value  of the distribution is chosen to fit the next-period consumer expectation for stock price plus dividend. The width of the distribution is determined by the variance
of the distribution is chosen to fit the next-period consumer expectation for stock price plus dividend. The width of the distribution is determined by the variance , the normalization of the probability distribution is guaranteed by
, the normalization of the probability distribution is guaranteed by .
.
 (13)
(13)
Thus we get the following expressions for the benefit optimized values for tendency for consumption , share demand
, share demand  and bond demand
and bond demand  for each generation3
for each generation3
 (14)
(14)
 (15)
(15)
 (16)
(16)
where  is the discounted expected future income:
is the discounted expected future income:
 (17)
(17)
 (18)
(18)
 (19)
(19)
The functions  provide the optimum with respect to tendency of consumption, investment in shares or bonds, as a function of the prices
provide the optimum with respect to tendency of consumption, investment in shares or bonds, as a function of the prices  and
and  and wealth
and wealth , as well as expectations
, as well as expectations  and
and . The optimal consumption is a fraction
. The optimal consumption is a fraction  of the sum of current wealth
of the sum of current wealth  and the discounted expected income
and the discounted expected income . This amount is referred to as lifetime earnings. The percentage of consumption only depends on the discount factor
. This amount is referred to as lifetime earnings. The percentage of consumption only depends on the discount factor 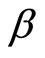 and is independent from expectations of future financial market prices.4 For the consumer only the wealth
and is independent from expectations of future financial market prices.4 For the consumer only the wealth  is directly available. The quantity
is directly available. The quantity  has to be compensated by short-selling of bonds. For this reason the term
has to be compensated by short-selling of bonds. For this reason the term  appears in the function for the bond demand. The optimum volume of shares is determined by the variable
appears in the function for the bond demand. The optimum volume of shares is determined by the variable , which is only influenced by present
, which is only influenced by present  and via
and via  by expected
by expected  financial market prices.
financial market prices.
In order to get a quantitative evaluation of the model, a concrete behavior of how the consumers form their expectations regarding the financial market variables has to be assumed. For consumer expectations the following assumptions are made: Each consumer assumes to achieve in a future period the income that a consumer of the appropriate age, in the current period receives:
 (20)
(20)
Regarding the bond yield consumers expect stability of the current value.
 (21)
(21)
For the expectation of future stock prices including dividends , the consumer corrects in each period, its previous expectations
, the consumer corrects in each period, its previous expectations , using an error correction by means of a weighted
, using an error correction by means of a weighted  prediction error
prediction error :
:
 (22)
(22)
This model accounts only for the stock prices in the past. One can also think of using models that consider consumer’s expectations about future stock prices and dividends: The knowledge of a pending asset market meltdown might lead to different investment behaviour of the consumers. The result will be an earlier reduction of stock investments and therefore a smearing out of the decrease of stock prices (see Poterba [6]). We decided not to include future predicitons in our modell because of two reasons: On the one hand there is currently no clear empirical prove for a connection between demographics and stock prices. We think this is necessary in order to convince the consumers to incorporate this fact in their investment decision. On the other hand short term effects will effect the decisions more than a long term meltdown (see Turner [7]).
2.3. Model of Company Decisions
In this section, the production and investment behavior of the business side is modeled. For simplicity, only one company is considered. In each period  the firm uses its capital stock
the firm uses its capital stock  and labor
and labor  to produce. The production process in the form of the production function
to produce. The production process in the form of the production function  is exposed to random environmental influences
is exposed to random environmental influences :
:
 (23)
(23)
The time evolution of the capital stock is determined by the depreciation rate  and the investment
and the investment :
:
 (24)
(24)
The entrepreneurial investment decision  is financed only by issuing a number of bonds
is financed only by issuing a number of bonds  at unit price. In the following it is assumed that there is no proportionality between capital stock increase
at unit price. In the following it is assumed that there is no proportionality between capital stock increase  and the collected amount of money
and the collected amount of money  (e.g. Abel [8] or Altig et al. [9]). Instead, it is assumed that the larger the desired ratio of investment
(e.g. Abel [8] or Altig et al. [9]). Instead, it is assumed that the larger the desired ratio of investment  to existing capital stock
to existing capital stock  the more money must be taken in order to achieve the desired capital stock increase. The link is called “adjustment cost function”.
the more money must be taken in order to achieve the desired capital stock increase. The link is called “adjustment cost function”.
 (25)
(25)
 (26)
(26)
This function is discontinuous at . This reflects the fact that in case of no investment no money is needed, while at a minimal investment already fixed costs
. This reflects the fact that in case of no investment no money is needed, while at a minimal investment already fixed costs  accrue.
accrue.
The bonds that have been issued in period  in order to finance the investment decision generate the obligation to pay in period
in order to finance the investment decision generate the obligation to pay in period  the sum
the sum  to the investor. In addition to paying off the bonds, the company has to pay the gross wages. It is assumed that the remaining money will be fully distributed as dividends to shareholders. The dividend per share is therefore (where
to the investor. In addition to paying off the bonds, the company has to pay the gross wages. It is assumed that the remaining money will be fully distributed as dividends to shareholders. The dividend per share is therefore (where  is the total number of shares):
is the total number of shares):
 (27)
(27)
How does the company make decisions? What amount of labor is needed? How much should be invested? As part of the model it is believed that these decisions are made under the constraint of maximum dividend payments. On the one hand, the demand for a maximum dividend payout in the current period, determines the labor demand in this period, on the other hand, the desire to maximize the dividend of the subsequent period determines the investment decision. In detail: At a decision point, the company has a capital stock , knows the environmental impact
, knows the environmental impact  and the bond repayment
and the bond repayment  from the investment decision in the previous period. The gross wage
from the investment decision in the previous period. The gross wage  is treated here as a parameter. By partial derivation of (27) with respect to
is treated here as a parameter. By partial derivation of (27) with respect to  an extremum of dt for the labor demand
an extremum of dt for the labor demand
 (28)
(28)
at a given wage level  can be found.
can be found.
For the investment decision it is assumed that the dividend in the next period
 (29)
(29)
should be maximized. Here  is the expected wage level of the next period. With
is the expected wage level of the next period. With  from Equation (24) and partial derivative
from Equation (24) and partial derivative , zero-setting and using Equation (28) follows for the optimal investment level:
, zero-setting and using Equation (28) follows for the optimal investment level:
 (30)
(30)
This results in the bond offer
 (31)
(31)
For the specific determination of wage expectations  different models can be used. In this work, the assumption of constant wages is used:
different models can be used. In this work, the assumption of constant wages is used:
 (32)
(32)
2.4. Time Evolution of the Model and Formation of Equilibrium Price
Using the models derived in the previous sections for behavior of consumers and companies, we can now determine the market equilibrium. Within the sequential structure of the model this is done at a time  by means of five steps. From the previous period
by means of five steps. From the previous period  the population
the population , capital stock
, capital stock , company investment
, company investment , share and bond investment of consumers
, share and bond investment of consumers
 bond volume
bond volume  and bond yield
and bond yield  are given.
are given.
Step 1: At the beginning of the period the development of the population takes place. The population 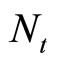 develops from
develops from  according to the model from Section 3.1. It follows the labor supply during the current period according to Equation (6). The capital stock of the current period is given by the capital stock and investments of the previous period from Equation (24).
according to the model from Section 3.1. It follows the labor supply during the current period according to Equation (6). The capital stock of the current period is given by the capital stock and investments of the previous period from Equation (24).
Step 2: Using the labor demand function of the company according to Equation (28), the labor supply Equation (6) and the assumption of a cleared labor market ( , full employment) it is possible to derive the equilibrium gross wage
, full employment) it is possible to derive the equilibrium gross wage  of the period
of the period :
:
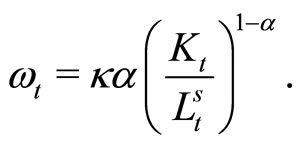 (33)
(33)
Depending on the preset contribution rate  of the pay-as-you-go system, the income of the consumers without investment income follows according to Equations (7) and (8). According to the effect of random production shock
of the pay-as-you-go system, the income of the consumers without investment income follows according to Equations (7) and (8). According to the effect of random production shock  the dividend payment
the dividend payment  for the current period is determined using Equation (27).
for the current period is determined using Equation (27).
Step 3: Based on these results each consumer forms the expectations for the next periods. For the income Equation (20) is valid, for the expected bond yield (21) is used and the expectations for the stock prices follow Equation (22). The companies make predictions on the wages of the next period according to Equation (32). Based on these expectations the consumers form their demand behavior according to Equations (14)-(16). The company determines the bond volume according to Equation (31).
Step 4: From the previous steps result share and bond demand and bond offering. The prices are obtained from market clearing conditions. These are for the stock and bond market:
 (34)
(34)
 (35)
(35)
Therefore we get for the actual period  the bond yield
the bond yield  and the stock price
and the stock price .
.
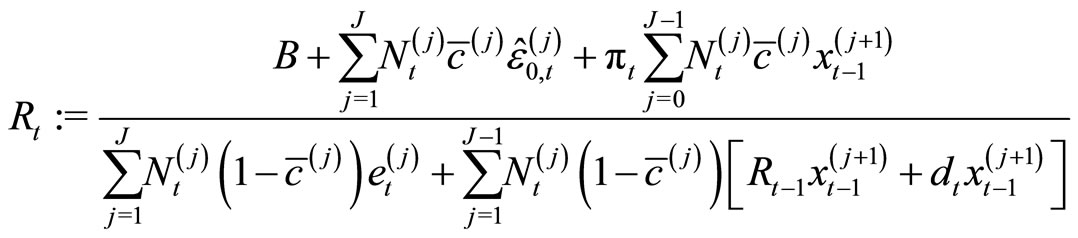
 (36)
(36)
with
 (37)
(37)
Here  is an adaption of the expectation
is an adaption of the expectation  to reality. The correction depends on the function
to reality. The correction depends on the function  which results from two nested implicit equations, which are listed here without derivation (see Hillebrand [5], pp. 67).
which results from two nested implicit equations, which are listed here without derivation (see Hillebrand [5], pp. 67).
 (38)
(38)
The auxiliary value  is derived from the solution of the following equation, where the finite limit of integration
is derived from the solution of the following equation, where the finite limit of integration  is chosen such that negative
is chosen such that negative  -values are prevented
-values are prevented
 (39)
(39)
For the previously determined prices, the consumer demand for stocks and bonds is satisfied and it is thus:
 (40)
(40)
 (41)
(41)
 (42)
(42)
Step 5: Finally, the individuals make their consumption decision and the company uses the money obtained by issuing bonds to fund the investments:
 (43)
(43)
 (44)
(44)
With this procedure, the development of the model is set within a period. For the next period in time the sequence begins again.
2.5. Calibration of the Model
In this section the parameters for the simulations are presented and motivated. The free parameters shall approximate reality. The values that are used have been derived from empirical studies.
For the simulations with the OLG-model at first a constant population with  consumers is assumed. Afterwards a dynamic population is studied. For life expectancy we use in both chapters
consumers is assumed. Afterwards a dynamic population is studied. For life expectancy we use in both chapters  and the retirement age is set to
and the retirement age is set to . Consequently, always 15 generations live at the same time. Thereof nine go to work and six are retired. Assuming that an individual consumes during 60 years (a childhood phase without consumption does not exist in the model), then a time step in the model corresponds to four years of life. Any consumer who is not already in retirement, provides one unit
. Consequently, always 15 generations live at the same time. Thereof nine go to work and six are retired. Assuming that an individual consumes during 60 years (a childhood phase without consumption does not exist in the model), then a time step in the model corresponds to four years of life. Any consumer who is not already in retirement, provides one unit  to the labor market. The discount rate
to the labor market. The discount rate , that is relevant for the optimization of the consumers, is taken from an empirical study (see Hurd [10], p. 801). This results in a discount rate of 0.011 corresponding to an annual discount factor of
, that is relevant for the optimization of the consumers, is taken from an empirical study (see Hurd [10], p. 801). This results in a discount rate of 0.011 corresponding to an annual discount factor of . With a time basis of four years
. With a time basis of four years  is obtained.
is obtained.
The constant parameters of the stock price expectancy are set to values of  for the maximum share price variation and
for the maximum share price variation and  is the width of the Gaussian distribution. The parameter
is the width of the Gaussian distribution. The parameter , that describes the temporal adjustment of the expectation value
, that describes the temporal adjustment of the expectation value  is set to
is set to . For the parameter
. For the parameter  in the production function empirical studies found values between 0.6 and 0.7. For the simulations a value of
in the production function empirical studies found values between 0.6 and 0.7. For the simulations a value of  is used. The parameter
is used. The parameter  in the production function serves essentially as a scaling factor and is set to the value
in the production function serves essentially as a scaling factor and is set to the value . The average annual depreciation rate in Germany between 1960 and 1990 was approximately 0.0528 (see Börsch-Supan et al. [11], p. 167). Within the four year period of the simulation step
. The average annual depreciation rate in Germany between 1960 and 1990 was approximately 0.0528 (see Börsch-Supan et al. [11], p. 167). Within the four year period of the simulation step  is therefore used. For the adjustment cost function
is therefore used. For the adjustment cost function  and
and  is used, in order to fit empirical studies (e.g. Abel [8] or Altig et al. [9]) in form of Equation (26). As a size for the production shocks
is used, in order to fit empirical studies (e.g. Abel [8] or Altig et al. [9]) in form of Equation (26). As a size for the production shocks  uniformly distributed random numbers between 0 and 2000 were used. As initial values we use for the capital stock
uniformly distributed random numbers between 0 and 2000 were used. As initial values we use for the capital stock , for stock prices including dividends
, for stock prices including dividends  and for bond yield
and for bond yield . Stock and bond volume are initially equally distributed across all generations.
. Stock and bond volume are initially equally distributed across all generations.
3. Simulation Results
In this section simulation results are presented which were determined using the previously described model. At first some basic properties of the model were demonstrated using a constant population. Then, the interactions between the pension system and an aging population are analyzed.
3.1. Results for a Constant Population
First of all, the possibilities of the model are shown for the case of a stationary population. The contribution rate is set to the value . The implementation of the simulation code was done using MATLAB.
. The implementation of the simulation code was done using MATLAB.
Figure 1 shows the time evolution of the model with the previously calibrated parameters and the presented population model. It reaches its equilibrium state already at , resulting in a constant labor supply
, resulting in a constant labor supply . Therefore the figure shows for
. Therefore the figure shows for  the dynamics of the other parameters for the case of a constant population. The figure also serves to verify the consistency of the simulation. For
the dynamics of the other parameters for the case of a constant population. The figure also serves to verify the consistency of the simulation. For  all parameters fluctuate around a fixed value. It turns out that the wages are very stable compared to the financial market variables. The fluctuations in stock prices including dividends
all parameters fluctuate around a fixed value. It turns out that the wages are very stable compared to the financial market variables. The fluctuations in stock prices including dividends  are essentially caused by the fluctuations of the stock prices themselves and to a small extent by the volatility of dividends. We also find, as expected, a positive correlation between stock prices and dividend payments. The bond yield
are essentially caused by the fluctuations of the stock prices themselves and to a small extent by the volatility of dividends. We also find, as expected, a positive correlation between stock prices and dividend payments. The bond yield  fluctuates around a value of 1.135, which corresponds to an annual interest rate of about 3%. This is consistent with the empirical expectation.
fluctuates around a value of 1.135, which corresponds to an annual interest rate of about 3%. This is consistent with the empirical expectation.
In order to investigate the influence of the pension system on the variables in the following the contribution rate  is varied (Figure 2). It is immediately obvious that when decreasing the contribution rate the capital stock increases. The basic assumption, that a funded system is superior to a pay-as-you-go system is depicted in the model. In addition, it can be seen that the average for the stock price including dividends decreases with an inc-
is varied (Figure 2). It is immediately obvious that when decreasing the contribution rate the capital stock increases. The basic assumption, that a funded system is superior to a pay-as-you-go system is depicted in the model. In addition, it can be seen that the average for the stock price including dividends decreases with an inc-

Figure 1. Time evolution of the simulation parameters for  and a constant population.
and a constant population.

Figure 2. Dependence on the contribution rate τ for the average values and standard deviations.
reasing contribution rate, whereas the bond yield increases.
Furthermore the variability around the time average (characterized by the standard deviation) increases significantly with increasing contribution rates. It can also be recognized that the model breaks down at a value of . Here individual consumers go bankrupt. This is not covered by the model and leads to its collaps. A more detailed analysis of the strong fluctuations shows that they are caused by fluctuations of the stock prices and not by the dividends. The wage level is largely independent of the contribution rate. Here also hardly any impact of the large fluctuations of the financial market variables for large contribution rates can be found.
. Here individual consumers go bankrupt. This is not covered by the model and leads to its collaps. A more detailed analysis of the strong fluctuations shows that they are caused by fluctuations of the stock prices and not by the dividends. The wage level is largely independent of the contribution rate. Here also hardly any impact of the large fluctuations of the financial market variables for large contribution rates can be found.
Figure 3 shows the steady state distribution across generations for the variables  (bonds),
(bonds), 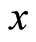 (shares),
(shares),  (wealth) and
(wealth) and  (consumption).
(consumption).
It is striking that young consumers secure credit by short selling of bonds. The borrowing is reduced with time, until for  the bonds become an investment opportunity. The high-risk form of investment in the stock market is used more specifically in young years, the shares are sold with age. This appears more strongly in the absence of a pay-as-you-go system (
the bonds become an investment opportunity. The high-risk form of investment in the stock market is used more specifically in young years, the shares are sold with age. This appears more strongly in the absence of a pay-as-you-go system ( ). In this case the wealth is for all times larger than with a pay-asyou-go system. The consumers successfully compensate the missing pension income in retirement age by additional capital income. The wealth reaches in both cases the maximum value just before the end of the working period. The consumption, however, rises in both cases monotonically with increasing age, where the increase for
). In this case the wealth is for all times larger than with a pay-asyou-go system. The consumers successfully compensate the missing pension income in retirement age by additional capital income. The wealth reaches in both cases the maximum value just before the end of the working period. The consumption, however, rises in both cases monotonically with increasing age, where the increase for  is steeper. This shows that without a pay-asyou-go system, consumption moves forward, and is even distributed more homogeneously over the many stages of life.
is steeper. This shows that without a pay-asyou-go system, consumption moves forward, and is even distributed more homogeneously over the many stages of life.
To assess which pension system is beneficial for the

Figure 3. Volume of bonds, shares, wealth and consumption across generations.
population, the lifetime welfare in the form of the following dimensionless variable is examined:
 (45)
(45)
For each time  the variable describes the welfare over the lifetime of a consumer belonging to generation
the variable describes the welfare over the lifetime of a consumer belonging to generation , who was born in period
, who was born in period  and will die at the end of period
and will die at the end of period . In Figure 4, this welfare function is shown.
. In Figure 4, this welfare function is shown.
For a stationary population, a higher contribution rate leads to a reduction of the lifetime welfare. Consequently, for a constant population the introduction of a pay-asyou-go system is not advisable. In an existing system, the contribution rates should be reduced in order to achieve a long-term gain of welfare for all generations. In the long run an existing pay-as-you-go system should be abolished. The problem is that following a reduction of contribution rates, the retired generation at this time suffers from welfare losses. It is important therefore, to make the changeover as gently as possible.
3.2. Results for an Aging Population
In this section we examine how the model responds to changes in population structure. The German population will age dramatically in the coming years. For a pension system the relevant parameter is the ratio of the number of contributors to the number of recipients (economic dependency ratio). There is a difference if we look at the entire population. This is based on the fact that not all young people are actually contributors (unemployment, employment inclination). Börsch-Supan et al. [11] investtigated the transfer of the elderly dependency ratio into predictions of the economic dependency ratio. It is essentially a scaled course of the elderly dependency ratio, with an increase of 66% in 2010 to one (scenario-dependent) rise up on a range of >100% by 2030.
In the model discussed here, all consumers are also

Figure 4. Welfare in case of a constant population for different contribution rates.
contributors, thus both parameters coincide. To simulate the aging curve, the birth development shown in Figure 8 was used. For  the population is constant. This initial time phase is used to bring the model to its steady state. At
the population is constant. This initial time phase is used to bring the model to its steady state. At  the onset of a demographic change is modeled by reducing the generation dependent birth rates
the onset of a demographic change is modeled by reducing the generation dependent birth rates  in each period by 1.4%. For
in each period by 1.4%. For  at each time step a reduced adjustment of the birth rates is applied in order to model the slower and almost linear increase of the elderly dependency ratio.
at each time step a reduced adjustment of the birth rates is applied in order to model the slower and almost linear increase of the elderly dependency ratio.
This results in the dependency ratio shown in the center graph of Figure 5. This model is close to the forecast. The development of the total population shown in the right graph is not very realistic. This is because part of the aging is due to an increase in life expectancy, while in the model all individuals always reach the same age. The aging therefore had to be fully modeled by changing the birth rates. In addition, the aging of the population was slowed in order not to overstretch the model (1 time step = 4 years).
Figures 6 and 7 show the time evolution of the model parameters for an aging population with contribution rates  and
and . Most striking is the drastic decline in stock prices and capital stock. Both variables are dramatically reduced. The drop is largely independent of the contribution rate and in the magnitude comparable to the decrease in the total population. This decline in stock prices is know as the phenomenon of “asset market meltdown” and has been predicted by several models (e.g. Abel [8]). Wages are rising slightly due to the scarcity of the labor supply. Also the bond yield increases slightly.
. Most striking is the drastic decline in stock prices and capital stock. Both variables are dramatically reduced. The drop is largely independent of the contribution rate and in the magnitude comparable to the decrease in the total population. This decline in stock prices is know as the phenomenon of “asset market meltdown” and has been predicted by several models (e.g. Abel [8]). Wages are rising slightly due to the scarcity of the labor supply. Also the bond yield increases slightly.
The impact on the welfare of consumers is shown in Figure 8 as the average of three different realizations of the random process in the production function. The curves follow the dependency ratio with a slight delay.
The decline is independent of the contribution rate. For  the decline is reduced and the welfare is always larger compared to the case of
the decline is reduced and the welfare is always larger compared to the case of . It turns out that
. It turns out that

Figure 5. Population dynamics in the model.

Figure 6. Parameter dynamics for  in presence of aging.
in presence of aging.

Figure 7. Parameter dynamics for  in presence of aging.
in presence of aging.

Figure 8. Welfare for constant contribution rate and demographic change.
demographic change with constant contribution rates will leads to drastic losses in consumer welfare.
3.3. Increasing the Contribution Rates
The decline of welfare, stock prices and capital stock as a result of demographic change raises the question whether it is possible to adapt the pension system in order to prevent or reduce these negative effects. In the following sections an existing pension system with a contribution rate of  and a retirement threshold of
and a retirement threshold of  is assumed.
is assumed.
One way to overcome this problem is to increase the contribution rate. Because fewer workers are facing more pensioners a higher contribution rate is needed in order to keep the pension level constant. In Germany, this is discussed in the form of the Riester/Rürup formula. In this approach, depending on the evolution of the salaries, the contribution rate in the two previous periods and the population growth, the contribution rate is increased. The dependence of consumer welfare by different variants of the formula was tested using the OLG model presented here already (e.g. Hillebrand [5], p. 159). The results achieved there are consistent with those achieved in the following using a simplified linear increase of the contribution rate. As the upper limit a value of  is assumed, because higher contributions are not politically feasible. In Figure 9 the development of welfare is shown for different contribution scenarios.
is assumed, because higher contributions are not politically feasible. In Figure 9 the development of welfare is shown for different contribution scenarios.
It is found that for all cases after the onset of demographic change at  the level of welfare can be stabilized at first. The level is sometimes even higher than the reference (
the level of welfare can be stabilized at first. The level is sometimes even higher than the reference ( const). The initial gain is bought dearly by a sharp drop in welfare later. Starting at
const). The initial gain is bought dearly by a sharp drop in welfare later. Starting at  all welfare curves with increasing contribution rates fall below the reference curve and stay there. An increase in the contribution rate is therefore not an appropriate means of preventing or dampening the loss of welfare. The welfare loss is delayed at first but will be more severe later.
all welfare curves with increasing contribution rates fall below the reference curve and stay there. An increase in the contribution rate is therefore not an appropriate means of preventing or dampening the loss of welfare. The welfare loss is delayed at first but will be more severe later.

Figure 9. Welfare in case of demographic change and increasing contribution rates.
3.4. Decreasing the Contribution Rates
As an alternative to an increase in contributions, in this section a contribution reduction or gradual abolition of the pay-as-you-go system is examined as a way to reduce the effects of demographic change. In Figure 4 it was shown that for a constant population a lower rate of contribution leads to welfare benefits. It therefore seems quite reasonable to use this potential welfare gain by lowering contribution to compensate for the loss caused by demographic effects. This is shown in Figure 10 for different contribution reduction scenarios.
For a very abrupt reduction of the contribution rate a reduction of welfare at  occurs, this is the result of the fact that these generations suffer from reduced pensions, but could not benefit from the low contribution rates during their working life. Afterwards for
occurs, this is the result of the fact that these generations suffer from reduced pensions, but could not benefit from the low contribution rates during their working life. Afterwards for  these cases show an increase of the welfare to values above the reference curve. This is due to the generations that benefit from the reduced contributions during their working period. This overshoot can be dampened when we pass to a slow reduction of the contributions. For all scenarios, finally the demographic effect prevails and results in a sharp decline in welfare. For all cases we find values for the welfare that lie after
these cases show an increase of the welfare to values above the reference curve. This is due to the generations that benefit from the reduced contributions during their working period. This overshoot can be dampened when we pass to a slow reduction of the contributions. For all scenarios, finally the demographic effect prevails and results in a sharp decline in welfare. For all cases we find values for the welfare that lie after  permanently above the reference curve. A reduction in contributions can therefore not prevent the loss of welfare. But it is possible to reduce the strength and to shift in time the decline of welfare.
permanently above the reference curve. A reduction in contributions can therefore not prevent the loss of welfare. But it is possible to reduce the strength and to shift in time the decline of welfare.
3.5. Raising the Retirement Age
The analysis so far has dealt only with the contribution rate adjustments to adapt the pension system to demographic development. If we assume that the retirement age is not determined by the physical abilities of workers but is determined by policy, this limit can be considered as a variable parameter. Furthermore, this is the only reform option that directly attacks the elderly dependency

Figure 10. Welfare in case of demographic change and decreasing contribution rates.
ratio by increasing the number of workers and reducing the number of pensioners. In previous studies a value of  has been consistently used. In Figure 11, the evolution of welfare for different time periods for the raising of the retirement age from
has been consistently used. In Figure 11, the evolution of welfare for different time periods for the raising of the retirement age from 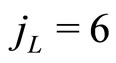 to
to  is shown. In all cases the contribution rate is decreased linearly between
is shown. In all cases the contribution rate is decreased linearly between  and
and  from
from 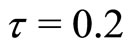 to
to .
.
Increasing the retirement age leads in the case of an early increase to a leap in the evolution of the welfare. This is due to the generations who receive an additional period of working income instead of a pension. Also, the pension of the older generations is increased. Nevertheless, the demographic effect leads to a decline in welfare. Compared to the scenarios with constant retirement age we find the possibility to reduce the decline of welfare. It is possible to get closer to the goal of a constant welfare if the retirement threshold is increased at a time around . Here the jump in welfare counteracts the demographic effect leading to a welfare evolution that is still decreasing but is much more stable than in previous cases. To ultimately find a welfare curve which is as flat as possible shorter time steps should be used.
. Here the jump in welfare counteracts the demographic effect leading to a welfare evolution that is still decreasing but is much more stable than in previous cases. To ultimately find a welfare curve which is as flat as possible shorter time steps should be used.
4. Conclusions
The impact of an aging population is broader than its financial impact on public budgets within a pay-as-yougo pension scheme. Demographic changes will affect the entire economy by affecting productivity, savings, consumption, interest rates and asset valuations. In the context of the introduced macroeconomic model, we have shown a drastic fall of capital market returns due to an aging population. Therefore, a capital funded pension system is also influenced negatively by demographic changes. Moreover, we examined which effect the demographic changes can have on the welfare of the individuals within a pay-as-you-go pension system. The increaseing aging of the population leads here to heavy falls in

Figure 11. Welfare in case of raising the retirement threshold and reduction of contribution rates.
individual welfare. Different reform variants of the pension system were examined.
An increase of pension age at simultaneous lowering of the contributions and gradual abolition of the financed pension system proves to be the best possibility not to remove but to reduce the welfare loss of the consumers due to demographic changes as far as possible. On the other hand, a policy with increases in contributions as a consequence of the demographic change shows the heaviest welfare losses. Taken into account the recent pension reforms in Germany (increase of regular retirement age from 65 to 67, introduction of a sustainability factor to limit the increase of contribution), a stronger increase in the retirement age or a faster transition from a pay-as-you-go pension system to a capital funded one would make sense from our point of view. But with an aging electorate, it is questionable whether such a policy will be enforceable (e.g. Shoven and Goda [12]).
NOTES
2Börsch-Supan and Ludwig [3] analyzed the effects of the aging process in France, Germany and Italy with pay-as-you-go-financed social security systems.
3The indices j and t are for clarity not explicitly specified in the following.
4This is a special property of the logarithmic utility function in Equation (12).