Production of J/Ψ-Particles at RHIC and LHC Energies: An Alternative “Psi”-Chology ()
1. Introduction
The study of the J/Ψ-mesons in ultra-relativistic heavy ion collisions has consistently been considered to be a potentially powerful tool for studying the properties of the hypothetical ‘hot and dense matter’ created in these collisions. Predictions about the suppression of J/Ψ-meson production in the nuclear collision, at certain stages [1] and an anomalous enhancement at certain other stage as well [2] are always treated as very powerful diagnostics. The deciding factor, in terms of the Standard Model (SM), in both the cases, is the number of charm-anticharm (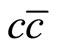 ) pairs (
) pairs ( ) created in the early stage of hard parton collisions in A + A (or in A + B) reactions. On the basis of it, one might arrive at the assumptions of the J/Ψ-suppression (at
) created in the early stage of hard parton collisions in A + A (or in A + B) reactions. On the basis of it, one might arrive at the assumptions of the J/Ψ-suppression (at  < 1) and the J/Ψ-enhancement (at
< 1) and the J/Ψ-enhancement (at  > 1) effects.
> 1) effects.
In the past, [3-5] we had constantly refrained from giving such undue importance to any controversy about either suppression/enhanced suppression or an enhancement of J/Ψ mesons in reality. Rather our primary intent would centre around understanding and interpreting the nature of data of inclusive cross-sections and some other important observables of J/Ψ mesons in BNL-RHIC and CERN-LHC experiments. In fact, we have an altogether different and heretic view (which will be outlined very briefly in the next section) about the mechanism of J/Ψ production in high energy particle and nuclear collisions.
We define our objectives here as: 1) to explain the main and major features of the latest data on J/Ψ-production in BNL-RHIC and CERN-LHC experiments from the proposed alternative approach built up by us in a set of previous works done in the both the remote and recent past [6,7] and 2) to compare our model-based calculations with some other competing models.
Our plan of work presented here is as follows. In Section 2, we provide brief outlines of the models chosen for this study. The Section 3 provides very brief outlines of the models which are founded on the gantlets of assumptions of the “Standard”-model and which have been reckoned with for the sake of comparison. In Section 4 we give the results and general discussion. And in the last section (Section 5) we offer the final remarks and the conclusions arrived at.
2. The Main Approach: An Outline
In the present work, we will make use of a theoretical model to interpret some of the latest and topical observables of the J/Ψ production which were measured and reported by the different groups in the Relativistic Heavy Ion Collider (RHIC) and Large Hadron Collider (LHC) experiments in the recent past. The model has a modest degree of dynamical basis and some prior check-ups with data [3-5]. It is called here as the sequential chain model (SCM).
The outline and features of the model we use here are obtained, in the main, from our previous works [3-5].
According to this model, high energy hadronic interactions boil down, essentially, to the pion-pion interactions; as the protons are conceived in this model as p = (π+π0ϑ), where ϑ is a spectator particle needed for the dynamical generation of quantum numbers of the nucleons. The multiple production of J/Ψ-mesons in a high energy proton-proton collisions is described in the following way. The secondary π-meson or the exchanged ϱ-meson emit a free ω-meson and pi-meson; the pions so produced at high energies could liberate another pair of free ϱ and trapped ω-mesons (in the multiple production chain). These so-called free ϱ and ω-mesons decay quite a fast into photons and these photons decay into Ψ or Ψ′ particles, which, according to this alternative approach is a bound state of  or
or 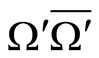 particles.
particles.
The inclusive cross-section of the Ψ-meson produced in the pp collisions given by
 (1)
(1)
where the expression for average multiplicity for Ψ-particles in pp scattering would be given by
 (2)
(2)
In the above expression, the term  is a normalisation parameter and is assumed here to have a value
is a normalisation parameter and is assumed here to have a value  0.09 for Intersecting Storage Ring (ISR) energy, and it is different for different energy and for various collisions. The terms
0.09 for Intersecting Storage Ring (ISR) energy, and it is different for different energy and for various collisions. The terms , x and
, x and  represent the transverse momentum, Feynman scaling variable and the rest mass of the J/Ψ particle respectively. Moreover, by definition,
represent the transverse momentum, Feynman scaling variable and the rest mass of the J/Ψ particle respectively. Moreover, by definition,  where
where 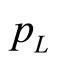 is the longitudinal momentum of the particle. The s in Equation (2) is the square of the cm energy.
is the longitudinal momentum of the particle. The s in Equation (2) is the square of the cm energy.
The second term in the right hand side of the Equation (1), the constituent rearrangement term arises out of the partonic rearrangements inside the proton. It is established that hadrons (baryons and mesons) are composed of few partons. These rearrangements mean undesirable loss of energy, in so far as the production mechanism is concerned. The choice of  would depend on the following factors: 1) the specificities of the interacting projectile and target; 2) the particularities of the seconddaries emitted from a specific hadronic or nuclear interaction and 3) the magnitudes of the momentum transfers and of a phase factor (with a maximum value of unity) in the rearrangement process in any collision. The parametrisation is to be done for two physical points, viz., the amount of momentum transfer and the contributions from a phase factor arising out of the rearrangement of the constituent partons. Collecting and combining all these, we propose the relation to be given by [8]
would depend on the following factors: 1) the specificities of the interacting projectile and target; 2) the particularities of the seconddaries emitted from a specific hadronic or nuclear interaction and 3) the magnitudes of the momentum transfers and of a phase factor (with a maximum value of unity) in the rearrangement process in any collision. The parametrisation is to be done for two physical points, viz., the amount of momentum transfer and the contributions from a phase factor arising out of the rearrangement of the constituent partons. Collecting and combining all these, we propose the relation to be given by [8]
 (3)
(3)
where  denotes the average number of participating nucleons and
denotes the average number of participating nucleons and  values are to be obtained phenomenologically from the fits to the data-points [9].
values are to be obtained phenomenologically from the fits to the data-points [9].
In order to study a nuclear interaction of the type A + B → Q + x, where A and B are projectile and target nucleus respectively, and Q is the detected particle which, in the present case, would be J/Ψ-mesons, the SCM has been adapted, on the basis of the suggested Wong [10] work to the Glauber techniques. The inclusive cross-sections for J/Ψ production in different nuclear interactions of the types A + B → J/Ψ + X in the light of this modified Sequential Chain Model (SCM) can then be written in the following generalised form as:
 (4)
(4)
where ,
,  and c are the factors to be calculated under certain physical constraints. The set of relations to be used for evaluating the parameters
and c are the factors to be calculated under certain physical constraints. The set of relations to be used for evaluating the parameters  is given below.
is given below.
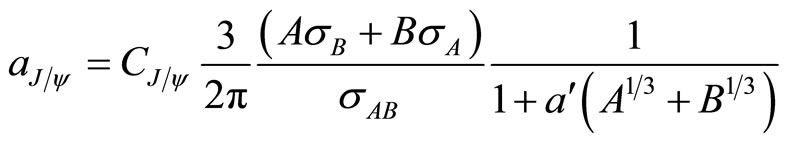 (5)
(5)
Here, in the above set of equations, the third factor gives a measure of the number of wounded nucleons i.e. of the probable number of participants, wherein 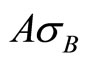 gives the probability cross-section of collision with ‘B’ nucleus (target), had all the nucleons of A suffered collisions with B-target. And
gives the probability cross-section of collision with ‘B’ nucleus (target), had all the nucleons of A suffered collisions with B-target. And  has just the same physical meaning, with A and B replaced.
has just the same physical meaning, with A and B replaced.
Besides, in expression (5), the fourth term is a physical factor related with energy degradation of the secondaries due to multiple collision effects. The parameter 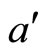 occurring in Equation (5) above is a measure of the fraction of the nucleons that suffer energy loss. The maximum value of
occurring in Equation (5) above is a measure of the fraction of the nucleons that suffer energy loss. The maximum value of 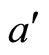 is unity, while all the nucleons suffer energy loss. This
is unity, while all the nucleons suffer energy loss. This  parameter is usually to be chosen [10], depending on the centrality of the collisions and the nature of the secondaries. The “a” factor in the expression (5) accommodates a wide range of variation because of the existence of the large differences in the in the normalizations of the J/Ψ cross-sections for different types of interactions.
parameter is usually to be chosen [10], depending on the centrality of the collisions and the nature of the secondaries. The “a” factor in the expression (5) accommodates a wide range of variation because of the existence of the large differences in the in the normalizations of the J/Ψ cross-sections for different types of interactions.
3. Some Competing Models: The Brief Outlines
3.1. The Gluon Saturation Approach
In this approach [11], it is assumed that the nuclear wave functions in very high-energy nuclear collisions can be described by the Color Glass Condensate (CGC). The primary effect is the suppression of J/Ψ production and narrowing of the rapidity distribution due to saturation of the gluon fields in heavy ion collisions relative to p + p collisions. In addition, the production mechanism is modified from p + p such that the multigluon exchange diagrams are enhanced in heavy ion reactions. It should be noted that this model does not include any hot medium effects, but does have a free parameter for the overall normalization factor.
3.2. The Quark Coalescence Model (QCM)
The Quark Coalescence Model (QCM) [12], is a twostage simulation. In stage I the incoming target and projectile nucleon interactions are tracked, a fluid of prehadrons is formed and in stage II the produced pre-hadrons interact and decay in a standard relativistic cascade model. The time history of all the collisions recorded in stage I sets up the geometry and initial conditions for stage II. Basic inputs for the simulation are measured hadron-hadron cross-sections, rapidity, transverse momentum and particle multiplicity distributions, of which the last are conforming to KNO scaling. The basic assumption of the model is coalescence of charm quarks and antiquarks into charmonia ( → charmonium), which can also be viewed as heavy pre-hadrons in stage I. Only a small percentage of charm quarks are expected to coalesce into bound charmonia i.e. J/Ψ, the remainder of such quarks appear ultimately as open charm mesons. At RHIC energies comover suppression of directly produced charmonia is expected to be large, due to the increased particle numbers and densities.
→ charmonium), which can also be viewed as heavy pre-hadrons in stage I. Only a small percentage of charm quarks are expected to coalesce into bound charmonia i.e. J/Ψ, the remainder of such quarks appear ultimately as open charm mesons. At RHIC energies comover suppression of directly produced charmonia is expected to be large, due to the increased particle numbers and densities.
3.3. Double Color Filter-Oriented Approach
A mechanism called double color filtering for  dipoles [13], makes nuclei significantly more transparent in AA than pA collisions. The assumption of this model is as follows: In the cm of nuclear collision the nuclear disks passing through each other leave behind a cloud of radiated gluons creating a dense matter, which the J/Ψ propagates through. In this reference frame the J/Ψ full momentum is
dipoles [13], makes nuclei significantly more transparent in AA than pA collisions. The assumption of this model is as follows: In the cm of nuclear collision the nuclear disks passing through each other leave behind a cloud of radiated gluons creating a dense matter, which the J/Ψ propagates through. In this reference frame the J/Ψ full momentum is , which ranges from zero to several GeV in RHIC data. Such a low energy
, which ranges from zero to several GeV in RHIC data. Such a low energy 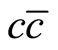 dipole develops the J/Ψ wave function pretty fast, during time
dipole develops the J/Ψ wave function pretty fast, during time  < 0.5 fm, which is about the time scale of the medium creation. Thus, what is propagating through the medium is not a small
< 0.5 fm, which is about the time scale of the medium creation. Thus, what is propagating through the medium is not a small  dipole, but a fully formed J/Ψ. The observed nuclear effects in J/Ψ production in AA collisions is interpreted as a combination of final state interaction (FSI) of J/Ψ in the dense medium, and the initial state interaction (ISI) effects in production of J/Ψ caused by multiple interactions of the colliding nuclei.
dipole, but a fully formed J/Ψ. The observed nuclear effects in J/Ψ production in AA collisions is interpreted as a combination of final state interaction (FSI) of J/Ψ in the dense medium, and the initial state interaction (ISI) effects in production of J/Ψ caused by multiple interactions of the colliding nuclei.
4. The Results
Now let us proceed to apply the chosen model to interpret some recent experimental results of J/Ψ-production reported by various groups for different collisions like p + p, d + Au, Cu + Cu, Au + Au at RHIC and p + p, Pb + Pb at LHC. Here, the main observables are the invariant yields, rapidity distributions and the nuclear modification factors which would come under purview of the present work.
4.1. J/Ψ (Total) Cross-Sections and Rapidity Distribution in p + p Interactions
As the psi-productions are generically treated rightly as the resonance particles, the standard practice is to express the measured J/Ψ (total) cross-sections times branching ratio to muon or electrons, i.e. for lepton pairs, that is by .
.
By using Expression (4) we arrive at the expressions for the differential cross-sections for the production of J/Ψ-mesons in the mid and forward-rapidities (i.e.  and
and 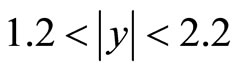 respectively) in p + p collisions at
respectively) in p + p collisions at  = 200 GeV at RHIC.
= 200 GeV at RHIC.

for  (6)
(6)
and
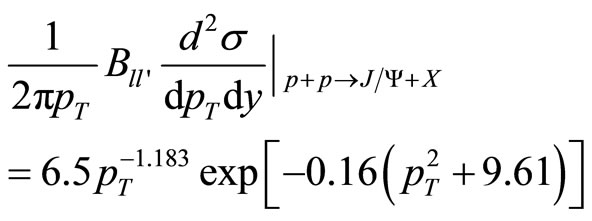
for  (7)
(7)
For deriving the Expressions (6) and (7) we have used the relation  [14], where
[14], where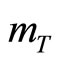 ,
,
 are the transverse mass of the produced particles and the rapidity distributions.
are the transverse mass of the produced particles and the rapidity distributions.  MeV [14] and
MeV [14] and , the branching ratio is for muons or electrons i.e. for lepton pairs
, the branching ratio is for muons or electrons i.e. for lepton pairs  is taken as
is taken as  [14] in calculating the above equations.
[14] in calculating the above equations.
In a similar fashion, the total inclusive cross-sections for the production of J/Ψ-mesons in different rapidities (i.e.,  and
and  respectively) in p + p collisions at
respectively) in p + p collisions at  = 7 TeV at LHC would be,
= 7 TeV at LHC would be,

for  (8)
(8)
and

for  (9)
(9)
For the calculation of the rapidity distribution from the Equation (4) we can make use of a standard relation as given below:
 (10)
(10)
For p + p collisions, the calculated rapidity distribution equation at RHIC-energy  = 200 GeV is
= 200 GeV is
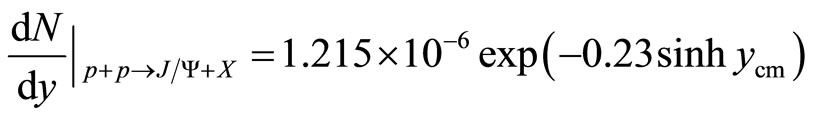 , (11)
, (11)
In a similar fashion, the SCM-based rapidity distribution equation at LHC-energy  = 7 TeV in p + p collisions has been given hereunder
= 7 TeV in p + p collisions has been given hereunder
 . (12)
. (12)
4.2. Invariant Yields in d + Au, Cu + Cu and Au + Au Collisions at RHIC-Energy
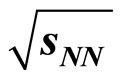 = 200 GeV
= 200 GeV
From the expression (4), we arrive at the invariant yields for the J/Ψ production in  reactions for mid and forward-rapidities.
reactions for mid and forward-rapidities.

for  (13)
(13)
and

for  (14)
(14)
For the case of Cu + Cu most central collisions (0% - 20%) at RHIC, the SCM-based calculated theoretical invariant yields for the rapidities 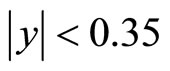 and
and  are given by the following equations respectively;
are given by the following equations respectively;

for , (15)
, (15)
and

for . (16)
. (16)
Similarly, for Au + Au collisions at  = 200 GeV at RHIC, the equations of transverse momenta spectra for 0% - 20% centrality regions are given by the undernoted relations.
= 200 GeV at RHIC, the equations of transverse momenta spectra for 0% - 20% centrality regions are given by the undernoted relations.

for ,(17)
,(17)
and

for . (18)
. (18)
For calculating the values of NR, in general, we have used the values of  from Refs. [11] and [15].
from Refs. [11] and [15].
4.3. The Nuclear Modification Factor RAB
There is yet another very important observable called nuclear modification factor (NMF), denoted here by  which for the production of J/Ψ is defined by [16]
which for the production of J/Ψ is defined by [16]
 (19)
(19)
The SCM-based results on NMFs for Cu + Cu and Au + Au collisions for forward rapidities are deduced on the basis of Equation (6), Equation (15), Equation (17) and Equation (19) and they are given by the undernoted relations
 , (20)
, (20)
and
 . (21)
. (21)
herein the value of  to be used is
to be used is  [17] for Cu + Cu collisions and for Au + Au collisions it is taken as
[17] for Cu + Cu collisions and for Au + Au collisions it is taken as  [18].
[18].
4.4. Analysis of the Figures
In Figures 1(a) and (b), we have drawn the total inclusive cross-sections for the production of J/Ψ-mesons in p + p collisions in different rapidities at RHIC and LHC energies 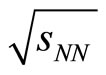 = 200 GeV and 7 TeV respectively. The solid lines in the figures are depicting the SCM modelbased results with the help of the Equations (6)-(9) while the experimental measurements are taken from Ref. [19, 20] respectively.
= 200 GeV and 7 TeV respectively. The solid lines in the figures are depicting the SCM modelbased results with the help of the Equations (6)-(9) while the experimental measurements are taken from Ref. [19, 20] respectively.
In Figure 2 we have plotted the rapidity distributions for J/Ψ-production in p + p collisions at  = 200 GeV. Data in the figure are taken from Ref. [21] and the line shows the SCM-based output.
= 200 GeV. Data in the figure are taken from Ref. [21] and the line shows the SCM-based output.
Similarly, in Figure 3, we have drawn the rapidity distribution  for J/Ψ production in p + p collisions at
for J/Ψ production in p + p collisions at  = 7 TeV as function of y. The solid lines depict the SCM-based results [Equation (12)] and the points indicate the experimental measurements [22].
= 7 TeV as function of y. The solid lines depict the SCM-based results [Equation (12)] and the points indicate the experimental measurements [22].

Figure 2. Plot of the rapidity distribution for J/Ψ production in proton-proton collisions at  = 200 GeV as function of y. The data points are from [15,21]. The solid curves show the SCM-based results (Equation (11)).
= 200 GeV as function of y. The data points are from [15,21]. The solid curves show the SCM-based results (Equation (11)).

Figure 3. Plot of the rapidity distribution for J/Ψ production in p + p collisions at  = 7 TeV as function of y. The data points are from [22]. The solid curves show the SCM-based results (Equations (15) and (16)).
= 7 TeV as function of y. The data points are from [22]. The solid curves show the SCM-based results (Equations (15) and (16)).
In Figure 4, we have drawn the solid lines depicting the SCM-based results for invariant yields for J/Ψ production in d + Au collisions at  = 200 GeV with the help of two Equations (13) and (14) against the experimental measurements [15].
= 200 GeV with the help of two Equations (13) and (14) against the experimental measurements [15].
The experimental results for the invariant yields of J/Ψ production as a function of transverse momenta for Cu + Cu collisions at  = 200 GeV are taken from Ref. [16] at centrality 0% - 20% and are plotted in Figure 5. The solid lines in the figure show the SCM-induced results.
= 200 GeV are taken from Ref. [16] at centrality 0% - 20% and are plotted in Figure 5. The solid lines in the figure show the SCM-induced results.

Figure 4. Plot of the invariant yields for J/Ψ production in d + Au collisions at  = 200 GeV as function of
= 200 GeV as function of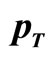 . The data points are from [15]. The solid curves show the SCMbased results.
. The data points are from [15]. The solid curves show the SCMbased results.
In the Figure 6, the solid lines are the plots of SCMbased invariant yields vs.  as described by Equations (17) and (18) at forward and mid-rapidities for Au + Au collisions at
as described by Equations (17) and (18) at forward and mid-rapidities for Au + Au collisions at 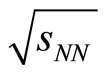 = 200 GeV, while the dotted curve in the Fig. shows results of coalescence model [12]. The experimental data points in the Figure 6 for the invariant yields of J/Ψ production as a function of transverse momenta at centrality values 0% - 20% and at the rapidities
= 200 GeV, while the dotted curve in the Fig. shows results of coalescence model [12]. The experimental data points in the Figure 6 for the invariant yields of J/Ψ production as a function of transverse momenta at centrality values 0% - 20% and at the rapidities  and
and  respectively are taken from the PHENIX Collaboration [15].
respectively are taken from the PHENIX Collaboration [15].

Figure 6. Plot of the invariant yields for J/Ψ production in Au + Au collisions at 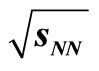 = 200 GeV as function of
= 200 GeV as function of . The data points are from [21]. The solid curve shows the SCM-based results while the dotted curve depicts the Coalescence Model [12].
. The data points are from [21]. The solid curve shows the SCM-based results while the dotted curve depicts the Coalescence Model [12].
In Figure 7(a), we plot  vs.
vs.  for 0% - 20% central region in Cu + Cu and Au + Au collisions at
for 0% - 20% central region in Cu + Cu and Au + Au collisions at  = 200 GeV. The solid lines in the figure show the SCM-based results (Equations (20) and (21)) against the experimentally measured results [15,16]. The dotted lines in the figure. represent the double Color Filtering approach [13].
= 200 GeV. The solid lines in the figure show the SCM-based results (Equations (20) and (21)) against the experimentally measured results [15,16]. The dotted lines in the figure. represent the double Color Filtering approach [13].
And in Figure 7(b), we plot  vs.
vs.  for 0% - 20% central region in Au + Au collisions at
for 0% - 20% central region in Au + Au collisions at  =
=
200 GeV and for Pb + Pb collisions at  = 2.76 TeV. The solid lines in the figure show the SCM-based calculations for different
part>’s. The Values of
part>’s are taken from Ref. [17]. The the experimentally measured results from Refs. [11,23] respectively. The dashed lines in the figure. represent the Gluon Saturation approach [11].
= 2.76 TeV. The solid lines in the figure show the SCM-based calculations for different
part>’s. The Values of
part>’s are taken from Ref. [17]. The the experimentally measured results from Refs. [11,23] respectively. The dashed lines in the figure. represent the Gluon Saturation approach [11].
5. Summary and Outlook
Let us first concentrate on what we have achieved here: 1) The features related to pT—spectra for J/Ψ production in some particle-particle and nuclear collisions at various high energies have been reproduced quite successfully; 2) The characteristics of rapidity spectra in p + p collisions at TeV energies have been brought out somewhat modestly satisfactorily; 3) The features of nuclear modification factors in Cu + Cu, Au + Au and Pb + Pb reactions at RHIC and LHC energies have also been brought out with the help of the applied model. Besides, some of our model-based results have also been compared with the performances on the same observables by some competing models of “standard” variety. And these comparisons with data and the results obtained by some other models reveal that SCM-based results describe the features of the data, at least, not inferior to the performance by the other approaches grounded on the “Standard” model ilk. In the past such were the recurrent observations made by us valid for many other obsevables measured in the various high statistics high energy particle and nuclear experiments.
Thus, summing up our past experiences and consider-
ing the weightage of the results reported here, we are forced to comment finally that this work essentially represents a case of paradigm shift in the domain of particle theory, as we have eschewed the conventional views of  approach to J/Ψ production in the “standard” framework. And this is just the reflection of our radical views about the particle structure and the nature of particle collisions. Obviously we obtain the fair agreement with data on some observables without inductions of 1) any QGP concept; 2) any prognosis of suppression or enhancement of J/Ψ-production. The production of J/Ψ- particles resembles all other hadrons.
approach to J/Ψ production in the “standard” framework. And this is just the reflection of our radical views about the particle structure and the nature of particle collisions. Obviously we obtain the fair agreement with data on some observables without inductions of 1) any QGP concept; 2) any prognosis of suppression or enhancement of J/Ψ-production. The production of J/Ψ- particles resembles all other hadrons.
6. Acknowledgements
The authors would like to express their thankful gratitude to the learned Referee for his/her valuable remarks and constructive suggestions in improving the earlier draft of the manuscript.
NOTES