MAC-PHY Cross-Layer for High Channel Capacity of Multiple-Hop MIMO Relay System ()
1. Introduction
Multiple-input multiple-output (MIMO) relay systems have been discussed in several literatures. Both the Gaussian MIMO relay channels with fixed channel conditions derive upper bounds and lower bounds that can be obtained numerically by convex programming. The upper bound and the lower bound on the ergodic capacity are found. In particular, for the case when all the nodes have the same number of antennas, the capacity can be achieved under the certain signal to noise ratio (SNR) condition [1-3]. Additionally, the ergodic capacity of the amplifyand-forward relay network is discussed. The links between the relay-transmitters and relay-receivers are assumed to be parallel [4] and serial [5,6]. Moreover, the endto-end channel capacity based on the different number of antennas at the transmitter, the relay and the receiver also has been evaluated [5,6]. However, the number of relays considered there (in [5] and [6]) is only one. The capacity of a particular large Gaussian relay network is determined by the limit as the number of relays tends to infinity. The upper bounds are derived from cut-set arguments, and the lower bounds follow an argument involving the uncoded transmission. It is shown that in case of interest, the upper and lower bounds coincide in the limit as the number of relays tends to infinity [7].
When the number of the relay antennas is less than the number of the transmit and receive antennas, the capacity of MIMO relay system is lower than that of the original MIMO system. Moreover, when the number of the relay antennas equals the number of the transmit and receive antennas or more, the MIMO relay system can provide the same average capacity as an original MIMO system. In other words, although the number of relay antennas is larger than the number of transmit and receive antennas, the capacity of MIMO relay system can’t exceed the capacity of original MIMO system [5,6,8-10].
Therefore, in order to achieve the high performance, the multiplehop relays system is considered. The diversity-multiplexing gain tradeoff (DMT) of multi-hop MIMO relay network with multiple antenna terminals in a quasi-static slow fading environment has also been considered. It is shown that the dynamic decode-andforward protocol achieves the optimal DMT if the relay is constrained to half-duplex operation. All the odd (or even) number hops is assumed to be operated simultaneously. However, the interference signal is assumed to be absent, and the perfomance based on a transmission protocol that only has two phases is analyzed [11]. The multiple-relay network, in which each relay decodes a selection of transmitted message by other transmitting terminals, and forwards parities of the decoded codewords, has been analyzed. This protocol improves the previously known achievable rate of the decodeand-forward strategy for multi-relay networks by allowing the relays to only decode a selection of messages from the relays with strong links to it [12].
However, in these papers the SNR at receiver(s) is assumed to be fixed and the location as well as the transmit power of each transmitter(s) are not dealt. In the multiple-hop MIMO relay system, when the distance between the source (Tx) and the destination (Rx) is fixed, the distance between the Tx to a relay (RS), RS to RS, RS to the Rx called the distances between transceivers, is shorten. Consequently, according to the number of relay and the location of the relays, the SNR and the capacity are changed. Hence, to achieve the high end-to-end channel capacity, the location of each relay meaning the distance between each transceiver needs to be optimized. We have analyzed the performance of half-duplex multiple hop relay system with the amplify-and-forward (AF) strategy [13]. We have obtained the high end-to-end channel capacity by optimizing the distance with equal transmit power. However, for achieving the higher endto-end channel capacity or in case the relay can’t be set at the desired location, the transmit power of each relay should be optimized. We propose the Markov Chain Monte Carlo method to optimize both the distance and the transmit power simultaneously. Additionally, the general transmission protocol on the Mac layer of multiplehop is analyzed based on the different propagation environment and the number of antennas at each relay. It is compared with Carrier Sense Multiple Access-Collision Avoidance protocol (CSMA-CA).
The rest of the paper is organized as follows. We introduce the concept of multiple-hop MIMO relays system in Section 2. Section 3 shows the optimization method for distance and the transmit power. The Mac layer protocol is described in Section 4. The end-to-end channel capacity of system with infinite number of antennas and relays is analyzed in Section 5. Finally, Section 6 concludes the paper.
2. Multiple-Hop MIMO Relays System
The multiple-hop MIMO relays system is described in details in [13]. However we choose some important parts to help the reader understand easier.
2.1. Channel Model
Figure 1 shows m relays intervened MIMO relay system. Let M, N and  denote the number of the antenna at the
denote the number of the antenna at the ,
, 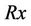 and
and , respectively. The
, respectively. The