Computation of the Multivariate Normal Integral over a Complex Subspace ()
1. Introduction
At testing many hypotheses with reference to the parameters of multivariate normal distribution, the problem of computation of multivariate normal integrals over a Complex Subspace of the following form arises [1]
 (1)
(1)
where  is the number of tested hypotheses
is the number of tested hypotheses  supposing that sample
supposing that sample  was brought about by distribution
was brought about by distribution

where  is the vector of distribution parameters and
is the vector of distribution parameters and  is the acceptance region of hypothesis
is the acceptance region of hypothesis 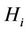 from sample space
from sample space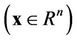
 , which has the following form
, which has the following form
 (2)
(2)
where ,
, .
.
Such regions of hypotheses acceptance arise, for example, in the generalized Neyman-Pearson criterion, and also in conditional Bayesian problems of testing many hypotheses [2,3]. The dimensionality of these integrals often reaches several tens when practical problems are solved. For example, in ecological problems the number of controlled parameters, according to which the decision is made, is quite often equal to several tens [4]; in the air defence problems, in particular, in the problems of tracking of flying objects using radar measurement information, the dimensionality of the problem is equal to the multiplication of the number of flying objects by the number of surveys made by the radar set [5] and so on. On the other hand, the time for solution of these problems is often limited and at times it plays a decisive role especially at solving the defence problems.
It is known that the complexity of realization and the obtained accuracy of numerical methods of computation of multidimensional integrals depend heavily on the dimensionality of these integrals and the complexity of the integration region configuration. In the considered case the integration regions are nonconvex and quite complex. Therefore it is difficult to realize the numerical methods and to provide the desired accuracy of calculation even when the dimensionality of integral is greater than or equal to three [6]. The methods of computation of the multivariate normal integral on the hyperrectangle offered in [7-12] are unsuitable for this case because of the complexity of the integration region.
Despite the convenience and the simplicity of computations, the Monte Carlo method is computer time consuming, especially at large dimensionality of integrals [3,13,14]. Therefore the method of approximate computation of integral (1) for a very short period of time is topical in many applications of mathematical statistics [15,16].
The aim of the present paper is the development of the method of computation of probability integral (1) with the desired accuracy in a minimum of time.
2. Problem Statement
Let us consider the case when the probability distribution density of the vector 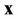 looks like
looks like
 (3)
(3)
where
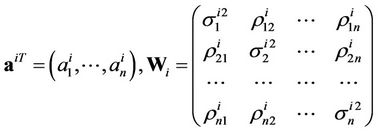 .
.
For probability distribution density (3), let us rewrite decision-making region (2) as
 , (4)
, (4)
where

 . (5)
. (5)
Random variables , are squared forms of the normally distributed random vector, and, if hypothesis
, are squared forms of the normally distributed random vector, and, if hypothesis 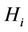 is true, their mathematical expectations are equal to
is true, their mathematical expectations are equal to
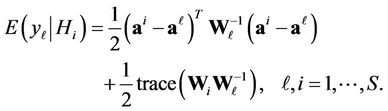 (6)
(6)
Therefore, if hypothesis  is true, the random variable
is true, the random variable  has noncentral distribution
has noncentral distribution 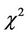 with the degree of freedom
with the degree of freedom  and with the parameter of noncentrality equal to (6) [2,17,18].
and with the parameter of noncentrality equal to (6) [2,17,18].
It is obvious that, at  and hypothesis
and hypothesis  is true, the random variable
is true, the random variable  has the central
has the central  distribution with the degree of freedom
distribution with the degree of freedom .
.
Let us write down (1) as follows
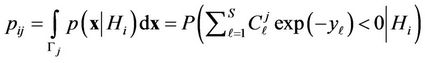 (7)
(7)
The task consists in the computation of probability (7). The method of its analytical computation is not known so far. For its computation it is possible, for example, to use a modified Monte-Carlo method (with the purpose of reducing the computation time) [3]. Though, at large , it still takes a good deal of time. The method of computation of probability (7) if hypotheses are formulated with reference only to the mathematical expectation of normally distributed random vector is offered in [3]. This method is unsuitable here, as the random variable
, it still takes a good deal of time. The method of computation of probability (7) if hypotheses are formulated with reference only to the mathematical expectation of normally distributed random vector is offered in [3]. This method is unsuitable here, as the random variable
 (8)
(8)
which formulates integration region (4), in [3] is the weighted sum of log-normally distributed random quantities;  and
and  are determined by formulae (5). In our case,
are determined by formulae (5). In our case,  is the weighted sum of the exponents of negative quadratic forms of the normally distributed random vector with correlated components.
is the weighted sum of the exponents of negative quadratic forms of the normally distributed random vector with correlated components.
Let us consider the case . In this case, regions (2) take the form
. In this case, regions (2) take the form


With taking into account probability densities (3), for these regions we derive
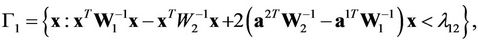

where

 .
.
Let us designate
 ,
,
 .
.
Then, finally, for the required regions, we shall obtain

 .
.
Each of random variables  and
and  is the sum of three random variables one of which is distributed by the normal law, and the two others are distributed by the
is the sum of three random variables one of which is distributed by the normal law, and the two others are distributed by the  law. Therefore, the probability distribution laws of random variables
law. Therefore, the probability distribution laws of random variables  and
and  have not closed forms.
have not closed forms.
Thus, at , i.e. at testing two hypotheses with respect to all parameters of multivariate normal distribution (in contradistinction to the case when hypotheses are formulated with respect to only the vector of mathematical expectation [3]), the principal complexity of the considered problem does not decrease.
, i.e. at testing two hypotheses with respect to all parameters of multivariate normal distribution (in contradistinction to the case when hypotheses are formulated with respect to only the vector of mathematical expectation [3]), the principal complexity of the considered problem does not decrease.
3. Computation of Probability Integral (7) by Series
Let us use the expanded form of representation of the quadratic form in (8) [18,19]. Then
 (9)
(9)
where  are the coefficients determined unambiguously by the elements of matrix
are the coefficients determined unambiguously by the elements of matrix  (see formula (3)).
(see formula (3)).
Let  be the conditional density of probability distribution of the random variable
be the conditional density of probability distribution of the random variable . Then, for (7), we obtain
. Then, for (7), we obtain
 . (10)
. (10)
Here the infinite interval  is taken as the domain of definition of random variable
is taken as the domain of definition of random variable 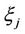 because of the signs of coefficients
because of the signs of coefficients  from (5).
from (5).
As was mentioned above, the probability distribution law of the random variable  has not a closed form. Let us consider the opportunity of approximating this density by series. For this reason we need the moments of the random variable
has not a closed form. Let us consider the opportunity of approximating this density by series. For this reason we need the moments of the random variable  [19-21]. Let us consider the problem of obtaining of these moments.
[19-21]. Let us consider the problem of obtaining of these moments.
With this purpose let us calculate the initial moment of the  th order of random variable
th order of random variable  provided that hypothesis
provided that hypothesis  is true
is true
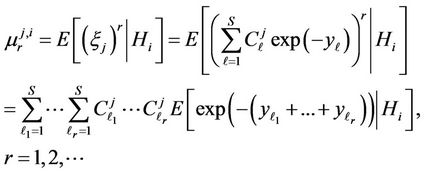 (11)
(11)
Expression  is the sum of correlated Quadratic Forms distributed by noncentral
is the sum of correlated Quadratic Forms distributed by noncentral  probability distribution laws. Because of correlation, the property of reproducibility of the
probability distribution laws. Because of correlation, the property of reproducibility of the 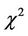 distribution does not take place [2,18], and, consequently the mathematical expectation in (12) has not a closed form.
distribution does not take place [2,18], and, consequently the mathematical expectation in (12) has not a closed form.
Let us use power series expansion of the exponent
 (12)
(12)
Let us use the expanded representation of quadratic form (9) and be satisfied with the first  terms of expansion (12). Then expression for calculation of moments (11) can be represented as follows
terms of expansion (12). Then expression for calculation of moments (11) can be represented as follows
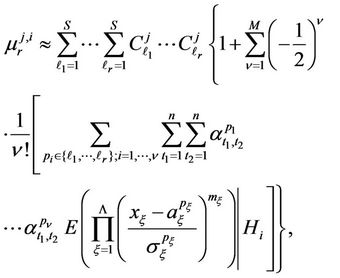 (13)
(13)
where 
 and
and  .
.
Expression (13) contains product moments [17,19,20] of the  (
( ) orders of normalized components of the correlated normally distributed random observation vector. Therefore, they are not equal to zero [18]. A lot of works are dedicated to the problem of computation of product moments [see, for example, 22-28].
) orders of normalized components of the correlated normally distributed random observation vector. Therefore, they are not equal to zero [18]. A lot of works are dedicated to the problem of computation of product moments [see, for example, 22-28].
In [22] the following problem was solved. Let  be random variables with mutually independent distributions, and let
be random variables with mutually independent distributions, and let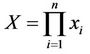 . There is found the probability that
. There is found the probability that  lies between
lies between  and
and , i.e.
, i.e.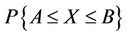 , by using the central limit theorem in accordance with which the random variable
, by using the central limit theorem in accordance with which the random variable  is approximately distributed by the normal law. The better is this approximation the bigger is
is approximately distributed by the normal law. The better is this approximation the bigger is .
.
The variance of the product of two random variables was studied by Barnett (1955) and Goodman (1960), in the case when they do not need to be independent. Shellard (1952) studied the case when the distribution of  was (approximately) logarithmic-normal. The author considered the case when
was (approximately) logarithmic-normal. The author considered the case when  are random variables with mutually independent distributions. For finding the probability that
are random variables with mutually independent distributions. For finding the probability that  lies between
lies between  and
and  , i.e.
, i.e. , the central limit theorem is used to approach the probability distribution of the random variable
, the central limit theorem is used to approach the probability distribution of the random variable  by normal distribution and this approach is better at increasing
by normal distribution and this approach is better at increasing . In work [25] no assumption is made about the distribution of
. In work [25] no assumption is made about the distribution of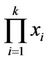 . There is discussed the case when the
. There is discussed the case when the  random variables,
random variables,  ,
,  are mutually independent, and the case when they do not have to be independent, and there are obtained their variance formulae. These results are generalizations of the results presented in [24].
are mutually independent, and the case when they do not have to be independent, and there are obtained their variance formulae. These results are generalizations of the results presented in [24].
In [26] are given exact formulae for the mathematical expectation of  and
and  ,
,  , where
, where  is the sample mean of the
is the sample mean of the 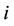 th “character” in a sample of
th “character” in a sample of 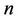 elements from a population of
elements from a population of  elements and
elements and  is the corresponding population mean. Formulae for estimating these product moments from the sample were also given. These estimations are slightly biased. In [27] the unbiased estimate of the 4-variate product moment was obtained. Asymptotic results for the 3-variate and 4-variate product moments and their estimates were also obtained.
is the corresponding population mean. Formulae for estimating these product moments from the sample were also given. These estimations are slightly biased. In [27] the unbiased estimate of the 4-variate product moment was obtained. Asymptotic results for the 3-variate and 4-variate product moments and their estimates were also obtained.
In [28] is derived a formula for the product moment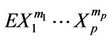 ,
,  in terms of the joint survival function when
in terms of the joint survival function when  is a non-negative random vector.
is a non-negative random vector.
From the given review (of course incomplete, because this is not the aim of this paper) of the works dedicated to the study of product moments, it is seen that the problem considered here differs from them.
Theorem 3.1. The initial moment of the  th order of random variable
th order of random variable  determined by (9), provided that hypothesis
determined by (9), provided that hypothesis 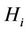 is true, can be calculated with any specified accuracy by the formula
is true, can be calculated with any specified accuracy by the formula
 (14)
(14)
where ;
;  and
and  are the matrices of eigenvectors and eigenvalues of the inverse covariance matrix of normalized random variables
are the matrices of eigenvectors and eigenvalues of the inverse covariance matrix of normalized random variables
 ;
; ,
, 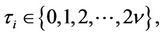
 , are the coefficients determined by the terms of matrices
, are the coefficients determined by the terms of matrices  and
and 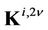 and vector
and vector ;
;  and
and 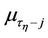 are the initial and central moments of the first and
are the initial and central moments of the first and  orders, respectively, defined by formulae (22), (23) and (24).
orders, respectively, defined by formulae (22), (23) and (24).
Proof. If hypothesis  is true, the values
is true, the values 
 are correlated normally distributed random variables with the parameters
are correlated normally distributed random variables with the parameters

 (15)
(15)
Thus, for calculation of moments (13), it is required to calculate the product moments of  -dimensional
-dimensional  normally distributed random vectors for which the components of the vectors of mathematical expectations and the covariance matrices are calculated by formulae (15).
normally distributed random vectors for which the components of the vectors of mathematical expectations and the covariance matrices are calculated by formulae (15).
Let us designate
 ,
,
 , (16)
, (16)
and the corresponding random vector—by
 , i.e.
, i.e.

For calculation of conditional product moments of the  -order, we have
-order, we have
 (17)
(17)
where  is the
is the  -dimensional normal probability distribution density with the vector of mathematical expectations and the covariance matrix calculated by formulae (16).
-dimensional normal probability distribution density with the vector of mathematical expectations and the covariance matrix calculated by formulae (16).
It is known that the value of integral (17) is invariant to linear transformation of the components of vector  [18] with the accuracy of Jacobian of Transformation. Let us designate the matrixes of eigenvectors and eigenvalues of matrix
[18] with the accuracy of Jacobian of Transformation. Let us designate the matrixes of eigenvectors and eigenvalues of matrix  by
by  and
and  , respectively. It should be pointed out that
, respectively. It should be pointed out that  is a diagonal matrix. Then the components of
is a diagonal matrix. Then the components of 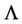 - dimensional random vector
- dimensional random vector
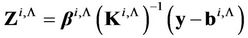 , (18)
, (18)
will be uncorrelated and will have standard normal distribution of probabilities [3,20].
From (18), we write
 .
.
Let us introduce the following designation
 .
.
Then, for the elements of the vector , we obtain the following expression
, we obtain the following expression
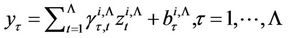 . (19)
. (19)
Using transformation (19), for mathematical expectation (17), we obtain
 (20)
(20)
where 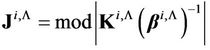 is the Jacobian of Transformation (18).
is the Jacobian of Transformation (18).
Let us raise to the powers the linear forms in the righthand side of expression (20) and group the identical items. Then (20) can be written as
 (21)
(21)
where, the coefficients of the identical items in (20) are designated by ,
, ; the items of the vector
; the items of the vector  are determined as
are determined as

It is known that [21,29]
 (22)
(22)
where  and
and  are the initial and central moments of
are the initial and central moments of  and
and  orders, respectively, of random variable
orders, respectively, of random variable . After simple routine transformations, for the considered case we obtain
. After simple routine transformations, for the considered case we obtain
 (23)
(23)
Here
 (24)
(24)
Taking advantage of ratios (21), (22), for computation of the moments (13), we obtain expression (14).
Probability integral (10) can be computed with the help of Edgewort’s series [19-21] using formula (14) for computation of the initial moments of random variable (9). In particular, in the considered case, using wellknown techniques of obtaining Edgewort’s series [30], we have
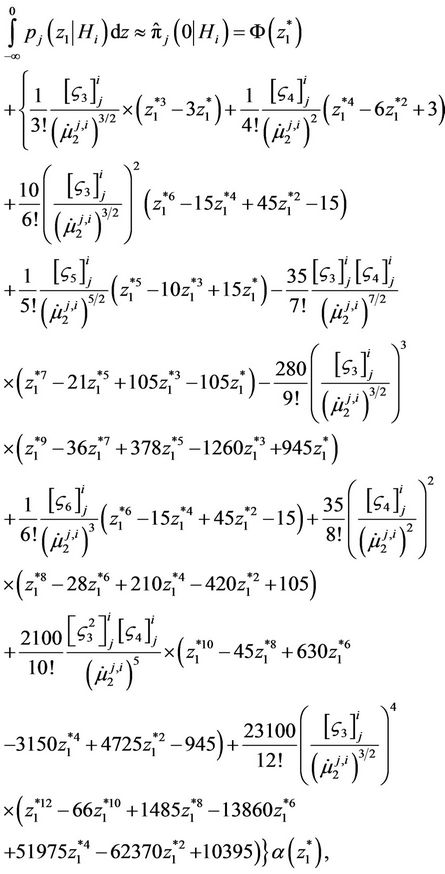 (25)
(25)
where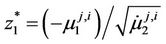 ;
; ,
,  is the
is the  th semi-invariant of the random variable
th semi-invariant of the random variable  provided hypothesis
provided hypothesis  is true (the computation of semi-invariants is not difficult knowing all initial moments includeing
is true (the computation of semi-invariants is not difficult knowing all initial moments includeing  (see, for example, [21]));
(see, for example, [21]));  is the second central moment;
is the second central moment;  is standard normal density, i.e.
is standard normal density, i.e.
 .
.
Satisfying the first seven terms in expansion (25), the absolute value of calculation error of the probability integral is calculated by the formula

The variable  is continuous and unambiguously defined for every value of
is continuous and unambiguously defined for every value of . Therefore, the random variable
. Therefore, the random variable  is continuous. The characteristic function of the random variable
is continuous. The characteristic function of the random variable  and its derivatives of any order exist, as the moments of any order of this random variable exist. At the same time, the characteristic function is uniformly continuous. Consequently, the distribution function of this random variable exists and is continuous [21].
and its derivatives of any order exist, as the moments of any order of this random variable exist. At the same time, the characteristic function is uniformly continuous. Consequently, the distribution function of this random variable exists and is continuous [21].
Theorem 3.2. The distribution function of random variable 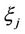 exists and is uniquely determined by moments (14).
exists and is uniquely determined by moments (14).
Proof. For proving this theorem, it is necessary to show that all moments  exist and the following condition takes place [19,21]
exist and the following condition takes place [19,21]
 .
.
The fact that all moments exist is obvious from formula (14) as by using it, it is possible to calculate the moments of any order with any specified accuracy. The values of these moments exist and are finite.
When solving the practical problems coefficients  take on the values bounded above; correlation matrices
take on the values bounded above; correlation matrices  are positively determined matrices the determinants of which differ from zero. Therefore, coefficients
are positively determined matrices the determinants of which differ from zero. Therefore, coefficients  are bounded-above quantities.
are bounded-above quantities.
There takes place

where 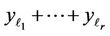 is the sum of quadratic forms of normally distributed
is the sum of quadratic forms of normally distributed  -dimensional vector
-dimensional vector  at different vectors of mathematical expectations and covariance matrices. Therefore, at changing components of the vector
at different vectors of mathematical expectations and covariance matrices. Therefore, at changing components of the vector  from
from  up to
up to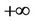 , the quadratic form
, the quadratic form  takes the values from 0 to
takes the values from 0 to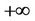 , and the value of function
, and the value of function  varies from 1 to 0, respectively. Therefore [18]
varies from 1 to 0, respectively. Therefore [18]
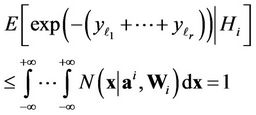
Thus, taking into account (5) and (11) we can write down

where  is the maximum by absolute value among coefficients
is the maximum by absolute value among coefficients .
.
Assume , then we have
, then we have
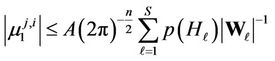 .
.
Let us designate . Then
. Then
 .
.
If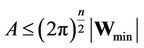 , then
, then  and it is not difficult to be convinced that
and it is not difficult to be convinced that  at
at .
.
Let , where
, where . Hence
. Hence
 and
and

at , which proves the theorem.
, which proves the theorem.
4. Computation Results
The accuracy of this algorithm depends heavily on  - the number of used items in expansion (12). In order to increase the accuracy of approximation of the exponent for given
- the number of used items in expansion (12). In order to increase the accuracy of approximation of the exponent for given  and, in general, the reliability of computation in the tasks of hypotheses testing, it is expedient to perform first the normalization of initial data by formulae:
and, in general, the reliability of computation in the tasks of hypotheses testing, it is expedient to perform first the normalization of initial data by formulae:

where ,
,  , are the minimum and maximum values of the
, are the minimum and maximum values of the  th parameter for the given set of the considered hypotheses, i.e.
th parameter for the given set of the considered hypotheses, i.e. ,
,  ,
,
 ,
,  [3]. In this case, the values of the parameters of the algorithm
[3]. In this case, the values of the parameters of the algorithm  and seven items in expansion (25) provided the absolute error of computation of integral (1) that does not exceed 0.005 for computed examples (see below). This fact was established by modeling for the observation vector with noncorrelated components. Unfortunately, by now the considered algorithm has been realized only for such a case [31].
and seven items in expansion (25) provided the absolute error of computation of integral (1) that does not exceed 0.005 for computed examples (see below). This fact was established by modeling for the observation vector with noncorrelated components. Unfortunately, by now the considered algorithm has been realized only for such a case [31].
The results of simulation showed that the time of execution of the task (decision-making and computation of the suitable value of the risk function) by using the Monte-Carlo method made up  sec,
sec,  sec, and
sec, and 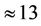 sec for the number of hypotheses
sec for the number of hypotheses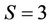 ,
,  and
and , respectively, the dimensionality of the observed vector being equal to
, respectively, the dimensionality of the observed vector being equal to  in all cases. The tested hypotheses and correlation matrix for the case
in all cases. The tested hypotheses and correlation matrix for the case 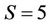 are given in tables of Figure 1 and Figure 2, respectively. Figures are presented as the suitable forms of the task of hypotheses test of the statistical software in which the appropriate methods are realized [31]. For other values of
are given in tables of Figure 1 and Figure 2, respectively. Figures are presented as the suitable forms of the task of hypotheses test of the statistical software in which the appropriate methods are realized [31]. For other values of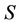 , there are chosen the suitable sub-sets of the tables of these Figures. In the first column of the table of Figure 1 is given the vector of measurements and in the other columns are given hypothetical values of mathematical expectation of this vector.
, there are chosen the suitable sub-sets of the tables of these Figures. In the first column of the table of Figure 1 is given the vector of measurements and in the other columns are given hypothetical values of mathematical expectation of this vector.
Meanwhile, when using the method offered here, the computation time did not practically change and the results were obtained for the time noticeably less than 1 sec. In both cases probability integrals (7) were computed with the accuracy of . In Figures 3 and 4 are given the dependences of the integral computation time on the accuracy and number of tested hypotheses respecttively.
. In Figures 3 and 4 are given the dependences of the integral computation time on the accuracy and number of tested hypotheses respecttively.
At solving many practical problems, especially military problems [5,32], the dimensionality of the integrals

Figure 1. The form of entering the tested hypotheses and a measurement vector.

Figure 2. The form of entering the covariance matrix.
like (1) often is equal to several tens and difference between the computation time necessary for the considered methods is significantly longer than in the above mentioned case [14], whereas the computation time for solving the defence problems are of great importance.
The theoretical investigation of the dependence of the accuracy of computation of integral (1) on M-the number of items in expansion (13) is a challenging task. Therefore, at program realization of the offered algorithm and, in general, algorithms of such a kind, it is worthwhile to

Figure 3. Dependence of the integral computation time on the accuracy.

Figure 4. Dependence of the integral computation time on the number of hypotheses.
make parameter  and the number of items in expansion (25) external parameters of the program. This allows establishing their optimal values for each concrete case by experimentation depending on the desired accuracy of computation.
and the number of items in expansion (25) external parameters of the program. This allows establishing their optimal values for each concrete case by experimentation depending on the desired accuracy of computation.
5. Conclusion
The method of computation of the probability integral from the multivariate normal density over the Complex Subspace by using series and the reduction of dimensionality of the multidimensional integral to one without losing the information was developed. The formulae for computation of product moments of normalized normally distributed random variables were also derived. The existence of the probability distribution law of the weighted sum of exponents of negative quadratic forms of the normally distributed random vector was justified. The opportunity of its unambiguous determination by the computed moments was proved.