Homotopy Perturbation Method for Solving Moving Boundary and Isoperimetric Problems ()
1. Introduction
In the modeling of a large class of problems which comes up in science, engineering and economics, it is necessary to minimize amounts of a certain functional. Because of the key role of this subject, it has been considerable attention has been devoted to these kinds of problems. Such problems are called variational problems (see [1,2]).
Consider the simplest form of a variational problem as:
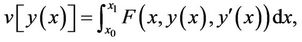 (1)
(1)
where v is the functional that its extremum must be achieved. There are two kinds of boundary conditions that functional v can be considered by. In the case of fixed boundary problems, the admissible function  must satisfy the boundary conditions
must satisfy the boundary conditions
 (2)
(2)
In moving boundary problems at least one of the boundary points of the admissible function is movable along a boundary curve. As a matter of fact, many applications of the calculus of variations lead to problems in which not only boundary conditions, but also conditions of quite a different type, known as constraints are imposed on the admissible function. The necessary condition for the admissible solutions at this problems is to satisfy the Euler-Lagrange equation which is mainly consider as nonlinear.
In this work we consider Homotopy perturbation method, which is an effective and applicable mathematical tool for linear and nonlinear equations. It yields a rapid convergence of the solution, and doesn’t have previous perturbation method limits (see [3-12]).
Author of [13] solved variational problems with moving boundaries with Adomian decomposition method.
In [14] Homotopy perturbation method applied to solve variational problems with fixed boundaries. In this paper solution of variational problems with moving boundaries problems can be obtained by Homotopy perturbation method first. Then we obtain solution of them by using combined homotopy perturbation method and Green’s function method. This algorithm is offered for the solution of second-order boundary value problems with two-point boundary conditions. To transform the ordinary differential equation into an equivalent integral one, which has already satisfied the boundary conditions, we apply the Green’s function method first. Then, the homotopy perturbation method is used to the resulting equation to construct the numerical solution for such problems. To illustrate a clear overview of the procedure several illustrative examples are involved.
2. Statement of the Problem
2.1. Moving Boundary Problems
The essential condition for the solution of problem (1) has been fulfilled the Euler-Lagrange equation
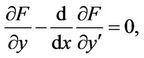 (3)
(3)
The general form of the variational problem (1) is
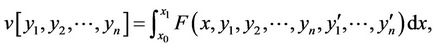 (4)
(4)
Here the necessary condition for the extremum of the functional (4) is satisfying the system of second-order differential equations below
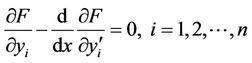 (5)
(5)
In the fixed boundary problems, Euler-Lagrange equation must be considered by the boundary conditions, but for the problems with variable boundaries, Euler-Lagrange equation has to satisfy natural boundary conditions or transversality conditions that has been discussed in the following theorems.
Type 1: Firstly, we consider problems for which at least one of the boundary points move freely along a line parallel to the y-axis, actually at this point  is not specified. In this case all admissible functions have the same domain of definition
is not specified. In this case all admissible functions have the same domain of definition  and satisfy the EulerLagrange equation in this interval. Furthermore such functions must satisfy conditions called natural boundary conditions prescribed in the following theorem.
and satisfy the EulerLagrange equation in this interval. Furthermore such functions must satisfy conditions called natural boundary conditions prescribed in the following theorem.
Theorem 2.1. Suppose the function  in
in , yields a relative minimum of the functional (1) for which
, yields a relative minimum of the functional (1) for which  is given,
is given,  is arbitrary (free right endpoint) or
is arbitrary (free right endpoint) or  are arbitrary (free endpoints).
are arbitrary (free endpoints).
Then  satisfies, respectively, the following natural boundary conditions:
satisfies, respectively, the following natural boundary conditions:
 (6)
(6)
Or
 (7)
(7)
Type 2: Secondly, we ought to turn to the beginning and end points (or only one of them) that move freely on given curves  In this case, we look for a function
In this case, we look for a function , which emanates at some
, which emanates at some  from the curve
from the curve  and terminates for some
and terminates for some  on the curve
on the curve  and minimizes the functional (1). In this problem the points
and minimizes the functional (1). In this problem the points  are unknown, they must satisfy the necessary conditions called transversality conditions, prescribed in the following theorem.
are unknown, they must satisfy the necessary conditions called transversality conditions, prescribed in the following theorem.
Theorem 2.2. If the function  which emanates at some
which emanates at some  from the curve
from the curve  and terminates for some
and terminates for some 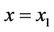 on the curve
on the curve  yields a relative minimum for functional (1), where
yields a relative minimum for functional (1), where  being a domain in the
being a domain in the  space that contains all lineal elements of
space that contains all lineal elements of , then it is necessary that
, then it is necessary that  must satisfy the Euler-Lagrange equation in the interval
must satisfy the Euler-Lagrange equation in the interval  and that at the point of departure and the point of arrival, the transversality conditions:
and that at the point of departure and the point of arrival, the transversality conditions:
 (8)
(8)
 (9)
(9)
are satisfied. In such a state that one of the points is fixed, then the transversality condition has to hold at the other point. One can consider transversality conditions for the problems with more than one unknown functions. For example, in the two dimensional case we seek a vector function  as minimizes
as minimizes
 (10)
(10)
in which  and the endpoint lies on a two-dimensional surface that is given by
and the endpoint lies on a two-dimensional surface that is given by  Here the transversality conditions at
Here the transversality conditions at  are:
are:
 (11)
(11)
 (12)
(12)
In which  is an admissible vector function.
is an admissible vector function.
For more information on transversality conditions, specially for the proofs of Theorems 2.1 and 2.2 and conditions (11), (12) (see [15]).
2.2. Isoperimetric Problems
Assume that two functions  and
and  are given. From among all curves
are given. From among all curves  along which the functional
along which the functional

assumes a given value l, determine the one for which the functional

assumes an extremal value. We assume that F and G have continuous first and second partial derivatives for  and for arbitrary values of the variables y and
and for arbitrary values of the variables y and .
.
Euler’s theorem: If a curve  extremizes the functional
extremizes the functional  subject to the conditions
subject to the conditions

and if  is not an extremal of the functional K, then there exists a constant λ, such that the curve
is not an extremal of the functional K, then there exists a constant λ, such that the curve  is an extremal of the functional
is an extremal of the functional

The vital condition for the solution of this problem is to satisfy the Euler-Lagrange equation

with given boundary conditions in which  see [15] for further information.
see [15] for further information.
3. Homotopy Perturbation Method
We consider the following nonlinear differential equation
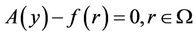 (13)
(13)
with natural boundary conditions or transversality conditions
 (14)
(14)
where A is a general differential operator, B is a boundary operator,  is a known analytic function and
is a known analytic function and  is the boundary of the domain
is the boundary of the domain .
.
The operator A can, generally, be divided into two parts L and N, where L is Linear, while N is nonlinear, so that we can write
 (15)
(15)
By Homotopy perturbation technique [3] and [4], we create a homotopy 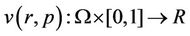 which satisfies
which satisfies
 (16)
(16)
Or
 (17)
(17)
where  is an embeding parameter, and
is an embeding parameter, and  is an initial approximation of Equation (13). Obviously from Equation (16):
is an initial approximation of Equation (13). Obviously from Equation (16):
 (18)
(18)
 (19)
(19)
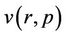 have to change from
have to change from  to
to  due to the changing process of p from zero to unity. In topology, this is named deformation, and
due to the changing process of p from zero to unity. In topology, this is named deformation, and  are called homotopic.
are called homotopic.
In this method, using the homotopy parameter p, we have the following power series in p
 (20)
(20)
Setting  results in the approximate solution of Equation (13)
results in the approximate solution of Equation (13)
 (21)
(21)
Numerical Examples
Example 3.1.1. Consider the following problems:
 (22)
(22)
In which  and
and  is the amount of a capital at time t. Here, the capital stock
is the amount of a capital at time t. Here, the capital stock  at the initial time
at the initial time  of the planning period is pretended to be known:
of the planning period is pretended to be known:  on the other hand, the planner will not want to prescribe how large the capital will be at time
on the other hand, the planner will not want to prescribe how large the capital will be at time . Hence, there exists a variational problem with free right endpoint. Here we let
. Hence, there exists a variational problem with free right endpoint. Here we let 
 and
and  which has the analytical solution
which has the analytical solution .
.
The Euler-Lagrange equation for this problem is:
 (23)
(23)
We know the natural boundary condition at  is
is
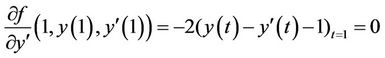 .
.
Therefore, we have the following boundary conditions for (3.1.2):
 (24)
(24)
We can readily construct a homotopy which satisfies
 (25)
(25)
With initial approximation , Suppose that the solution of Equation (25) has the (20).
, Suppose that the solution of Equation (25) has the (20).
Substituting (20) into (25), and equating the terms with the identical powers of p:
 ,
,
 ,
,
 .
.
assuming , we have
, we have , and
, and . So, for Equation (22) we have an approximate solution:
. So, for Equation (22) we have an approximate solution:
 . (26)
. (26)
Imposing (24) at (26), we have: .
.
Now we solve this problem with Adomian decomposition method. Using the operator form of (23), we have:
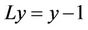 ,
,
 .
.
Applying the Adomian decomposition:
 .
.
So, we use the reccursive relations
 ,
,
 .
.
Now we use  as the approximation of y(x), for example, for
as the approximation of y(x), for example, for  we have:
we have:
 .
.
We solve the equation , for the determination of A. Table 1 shows the error of
, for the determination of A. Table 1 shows the error of .
.
Solutions of two methods show that the homotopy perturbation method is better than adomian decomposition method.
Example 3.1.2. We want to find the minimum of the integral  subject to the conditions
subject to the conditions
 (27)
(27)
From the auxiliary function [15]:
 (28)
(28)
A homotopy can be constructed as follows
 (29)
(29)
Our initial approximation is: . Supposing the approximate solution of Equation (29) has the form of (20), by the same manipulation like above example, we have
. Supposing the approximate solution of Equation (29) has the form of (20), by the same manipulation like above example, we have
 ,
,
 ,
,
 .
.
We suppose that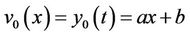 .
.
So 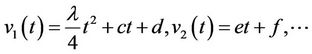
Therefore we find the following equation
 (30)
(30)
Imposing  on (30) we have:
on (30) we have:
 (31)
(31)
4. Combined Homotopy Perturbation Method and Green’s Function Method for Solving Second-Order Moving Boundary Problems
Assume that [16]
 (32)
(32)
with boundary conditions that obtained from transversality conditions. Where  is a real constant number,
is a real constant number,  is a nonlinear function, and
is a nonlinear function, and 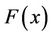 is a nonhomogeneous term.
is a nonhomogeneous term.
We can write Equation (32) to an equivalent integral equation;
 (33)
(33)
By adding a nonhomogeneous term, in moving boundary problems, the above equation is modified because boundary conditions are nonhomogeneous. Here, the function  the function
the function  that called Green’s function, is adjusted as below:
that called Green’s function, is adjusted as below:
 (34)
(34)
In Equation (33), if , then Green’s function amended as below:
, then Green’s function amended as below:
 (35)
(35)
We construct the homotopy form of Equation (33), which satisfies:
 (36)
(36)
The solution of the Equation (32) is assumed to be the power series of p as expressed in Equation (20) and substituting Equation (20) into (36) and equating the term with identical powers of p, The following equations can be obtained:
 ,
,

We obtain the approximate solution from Equation (20) by solving these integral equation. If we construct the homotopy as:
 (37)
(37)
where  is the exact solution of (32), then we have:
is the exact solution of (32), then we have:
 (38)
(38)
Equation (38) will give the exact solution.
Numerical Examples
Example 4.1.1. Considering Ramsey growth model, we have:
 (39)
(39)
Also we have:
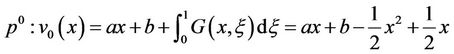 ,
,

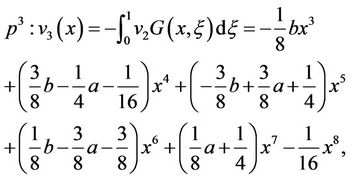

 .
.
Assume that  and by imposing boundary condition on that, we have:
and by imposing boundary condition on that, we have:

so:
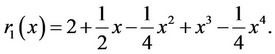
And assuming  and imposing boundary condition on that, we have:
and imposing boundary condition on that, we have:
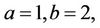
so:
 .
.
Also we can write:

But from (37) we have:

So:
 .
.
That is approach to exact solution. And also we obtain:
 .
.
The plot of  has been shown in Figure 1.
has been shown in Figure 1.
Example 4.1.2. We want to solve Example 3.1.2 with this method. The Euler-Lagrange equation is:
 .
.
Supposing  we have:
we have:

Figure 1. The plot of v0(x), r1(x), r2(x), r3(x) of Example 4.1.1.

and

So


by imposing boundary condition on that, we have:
 .
.
5. Conclusion
In this paper, we solve the moving boundary and isoperimetric problems by using Homotopy perturbation method. Embedding parameter  can be taken into account as a perturbation parameter. By the application of Green’s function, the problem concerned is transformed into an equivalent integral equation, which is solved using the homotopy perturbation method. Numerical examples show that these proposed methods were valid and effective for solving problems.
can be taken into account as a perturbation parameter. By the application of Green’s function, the problem concerned is transformed into an equivalent integral equation, which is solved using the homotopy perturbation method. Numerical examples show that these proposed methods were valid and effective for solving problems.