A Variational Approach for Numerically Solving the Two-Component Radial Dirac Equation for One-Particle Systems ()
1. Introduction
The study of hydrogen-like models plays an important role to test new approaches, and also in the description of the electronic structure of atomic and molecular systems. In this context, relativistic effects are of the most importance in a complete description of the physical system, mainly as the atomic mass of elements increases. Indeed, these effects play a crucial role in the description of the electronic structure of heavy elements.
Nevertheless, numerical methods used to take into account relativistic effects face several setbacks when the Dirac equation is used due to the existence of a negative continuum energy spectrum associated to the Dirac Hamiltonian operator, e.g., the appearance of instabilities in numerical calculations. Such methodologies are based on straight minimization of the expected values of the Dirac Hamiltonian with respect to a subset of the possible Dirac spinors [1-8]. As it is well known, it is very difficult to describe systems of many-electron atoms and molecules using the relativistic quantum mechanics approach. Even, in the Dirac’s relativistic framework, where a oneelectron spinorial solution is a two-vector whose components are scalar wave functions, the description is incomplete. Hence, a full relativistic description of the atomic and molecular electronic structure demands the application of Quantum Electrodynamics methods and consequently, the difficulty of implementing computational treatment for many-electron system increases. A survey of the currently available analytical solutions for relativistic one electron atoms may be found in Maple or Mathematica codes in [9,10] which may be valuable in comparing results of different theories.
In this paper, we propose an alternative approach that allows a simple numerical calculation to attain higher accuracy and allows comparison to other results. We improve the numerical methods to solve the Dirac equation, with special attention to the work of Drake and Goldman [11]. In this way we re-express the problem as one of finding the solution of the variation of a one-dimensional Lagrangean function. This Lagrangean is constructed as a positive definite function for particle energy eigenvalues, the antiparticle ones being get simply by sign reversion. This approach simplifies the procedure of finding the eigenvalues associated with a two-spinor subspace because it avoids automatically the variational collapse problem that always appears when considering the whole eigenvalue spectrum. The numerical procedure is done by calculating the algebraic variations of trial functions. This trial function we calculated in Section 3 for oneelectron bound systems, i.e., is similar to the Hylleraas computation method. Furthermore, the reduction to a two-dimensional Dirac-like equation is done by using transformation properties between noninertial frames, which will be useful in condensed matter such nanostructure, graphene and so on investigation. But for the applications in many-electrons as atomic and molecular systems the analytical equation given in [12] is not applicable. This paper goal is to obtain a numerical solution of the approach given in [12] to be useful in many-electrons applications. We should point out, as far we know from the literature, our method to obtain the energy values of the Dirac-Coulomb problem derives directly from the Dirac equation and not from the usual minimization procedures of the Dirac Hamiltonian. In this context the results presented in the paper are new. Although the theoretical aspects have been discussed [12] in order to make the paper more self-contained, we devote Section 2 to a short review of the mathematical tools of that reference. In Section 3 we develop the numerical methods and apply them to hydrogen isoelectronic atoms showing its consistency and high accuracy, relative to the exact analytical eigenvalues. The conclusions are summarized in Section 4.
2. An Irreducible 2D Form for the Dirac Equation
The Dirac wave equation [13] is naturally associated with complex manifolds of the form , with
, with . The usual 4D representation demands that
. The usual 4D representation demands that 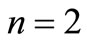 because the electron spin is introduced as an implicit or algebraic degree of freedom, which implies the need of four
because the electron spin is introduced as an implicit or algebraic degree of freedom, which implies the need of four  linearly independent matrices to construct the standard 4-spinor Dirac equation. However, we will show here that an irreducible 2D representation is also possible in
linearly independent matrices to construct the standard 4-spinor Dirac equation. However, we will show here that an irreducible 2D representation is also possible in  for a hydrogen-like problem. In future we expect generalize the procedure for many electron problems, by considering other
for a hydrogen-like problem. In future we expect generalize the procedure for many electron problems, by considering other  sets.
sets.
Since objects of , that is the SU2 group are complex
, that is the SU2 group are complex  quadratic matrices, [14] the corresponding wave function must be a two-spinor of the form
quadratic matrices, [14] the corresponding wave function must be a two-spinor of the form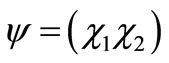 , so that we consider the stationary Hamiltonian problem
, so that we consider the stationary Hamiltonian problem
 (2.1)
(2.1)
with
 (2.2)
(2.2)
with  being the usual Pauli matrices. In order to investigate what angular momentum corresponds to a constant of motion in this model we consider the z component of the angular moment vector
being the usual Pauli matrices. In order to investigate what angular momentum corresponds to a constant of motion in this model we consider the z component of the angular moment vector
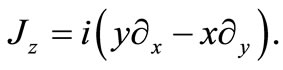 (2.3)
(2.3)
Equation (2.3) can easily be verified that do not commute with the Hamiltonian H
 (2.4)
(2.4)
However, we should observe that
 (2.5)
(2.5)
so that the effective operator,
 (2.6)
(2.6)
commutes with H and therefore is a constant of motion. In this context, M and H may be simultaneously diagonalized, that is
 (2.7)
(2.7)
where  is an eigenvalue of M.
is an eigenvalue of M.
In order to check if our irreducible Dirac equation generates the correct one particle solution, we consider a Coulomb potential , where
, where 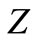 is the nuclear charge and
is the nuclear charge and  is the fine structure constant and determines the energy levels for hydrogenic atoms.
is the fine structure constant and determines the energy levels for hydrogenic atoms.
Equation (2.1) is explicitly written as a two component Dirac-like linear systems of equations
 (2.8a)
(2.8a)
and
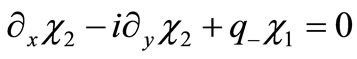 (2.8b)
(2.8b)
where we have introduced .
.
In ordinary polar coordinates , the differential operators in Equations (2.7) and (2.8) become
, the differential operators in Equations (2.7) and (2.8) become
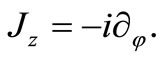
 (2.9)
(2.9)
By substituting Equation (2.9) into Equation (2.7) and Equations (2.8), it is straightforward to verify that the general solutions are
 (2.10a)
(2.10a)
 (2.10b)
(2.10b)
The exact solution has recursion relations given by
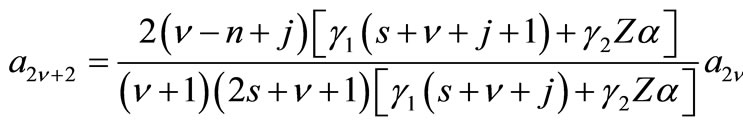 (2.11a)
(2.11a)
 (2.11b)
(2.11b)
where ,
, 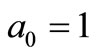 ,
,  with
with 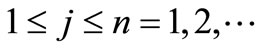 The remaining parameters are given by
The remaining parameters are given by  and
and . Finally, Equations (2.11) form a polynomial solution of finite degree for Equations (2.7) and (2.8), if and only if, the corresponding energy eigenvalues are given exactly by
. Finally, Equations (2.11) form a polynomial solution of finite degree for Equations (2.7) and (2.8), if and only if, the corresponding energy eigenvalues are given exactly by
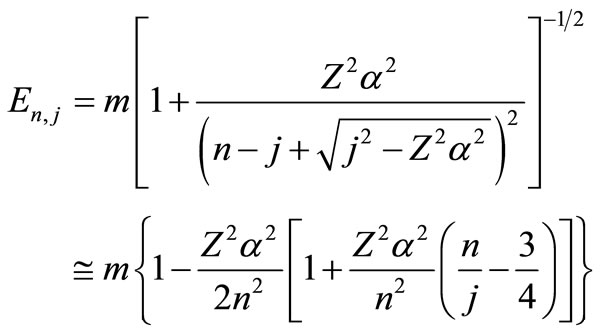 (2.13)
(2.13)
The first two radial functions  and
and 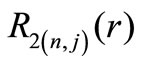 for the hydrogen ground state are
for the hydrogen ground state are
 (2.14a)
(2.14a)
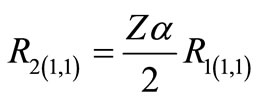 (2.14b)
(2.14b)
We would like to point out that the proportionality between  (the so called small component) and
(the so called small component) and  (the so called large component) observed in Equation (2.14) occurs only when
(the so called large component) observed in Equation (2.14) occurs only when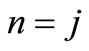 ; otherwise these functions are linearly independent.
; otherwise these functions are linearly independent.
3. Numerical Hylleraas-Like Variational Problem
We have seen in [12] that the method is analytically successful for one-electron atoms. We now formulate a numerical version, which is based in a Hylleraas-like variational approach given in [15], and aims to be extended to two or more electron systems in a future work. This time, instead of solving analytically the system composed of Equations (2.8), we isolate 
 (3.1)
(3.1)
and substitute into Equation (2.8b), obtaining
 (3.2)
(3.2)
We now express Equations (2.8) by means of an extremum problem in which the space integral of a general Lagrangean density  is stationary against small algebraic variations in the form of
is stationary against small algebraic variations in the form of  about the form of the exact eigenfunctions
about the form of the exact eigenfunctions  and
and
 (3.3)
(3.3)
given by
 (3.4)
(3.4)
which leads to the corresponding differential equation obeyed by the Lagrangean:
 (3.5)
(3.5)
where  is the complex conjugate of
is the complex conjugate of 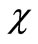 that satisfies the asymptotic condition
that satisfies the asymptotic condition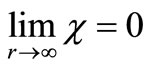 .
.
By comparing Equation (3.3) with Equation (3.5), it is clear that the only possible Lagrangean should be
 (3.6)
(3.6)
For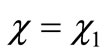 , we recover Equation (2.10a) or, making use of Equation (2.9) one obtains Equations (2.8). Now we construct a variation function by a product of a power series and undetermined coefficients times the exact solution in Equation (2.10b)
, we recover Equation (2.10a) or, making use of Equation (2.9) one obtains Equations (2.8). Now we construct a variation function by a product of a power series and undetermined coefficients times the exact solution in Equation (2.10b)
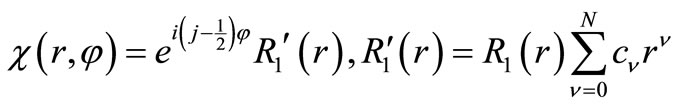 (3.7)
(3.7)
where N is an integer and to be specified later.
The variation process implied in Equation (3.4) is then performed directly, by requiring the vanishing of the partial derivatives of the integral of L with respect to the undetermined power series coefficients , whose values produce the algebraic variation of the form of
, whose values produce the algebraic variation of the form of  about the form of the exact eigenfunction
about the form of the exact eigenfunction , i.e.,
, i.e.,
 (3.8)
(3.8)
More explicitly, after substituting Equation (3.7) into Equation (3.6), the modified Lagrangean becomes
 (3.9)
(3.9)
Because the function  is not in general an eigenfunction of the Hamiltonian operator, Equation (3.7) does not lead naturally to a finite system of equations, as can be seen in Equation (2.8). Then it is necessary to truncate the power series of the modified function at same order of precision given by the integer N. In fact, Equation (3.7) leads us to an infinite system of linear equations such that the determinant must vanish in order to have a non trivial solution, so it has to be truncated, as usual in Hylleraas-like calculations, at a given order of precision [15]. The whole computational process is so simple that we could express and run the corresponding numerical algorithm using only what is available in Maple algebraic software.
is not in general an eigenfunction of the Hamiltonian operator, Equation (3.7) does not lead naturally to a finite system of equations, as can be seen in Equation (2.8). Then it is necessary to truncate the power series of the modified function at same order of precision given by the integer N. In fact, Equation (3.7) leads us to an infinite system of linear equations such that the determinant must vanish in order to have a non trivial solution, so it has to be truncated, as usual in Hylleraas-like calculations, at a given order of precision [15]. The whole computational process is so simple that we could express and run the corresponding numerical algorithm using only what is available in Maple algebraic software.
The numerical results of energies  in atomic units are calculated for the ground state and several excited states of hydrogen atom and are given in Table 1, in which dED stands for the numerical deviation with respect to the exact analytical values given in Equation (2.13). To obtain these results we have used N = 5 in Equation (3.7) and 4 iterations. Table 2 shows the set of
in atomic units are calculated for the ground state and several excited states of hydrogen atom and are given in Table 1, in which dED stands for the numerical deviation with respect to the exact analytical values given in Equation (2.13). To obtain these results we have used N = 5 in Equation (3.7) and 4 iterations. Table 2 shows the set of

Table 1. Relativistic energy of the ground and excited states for several n and j quantum numbers of atomic hydrogen.
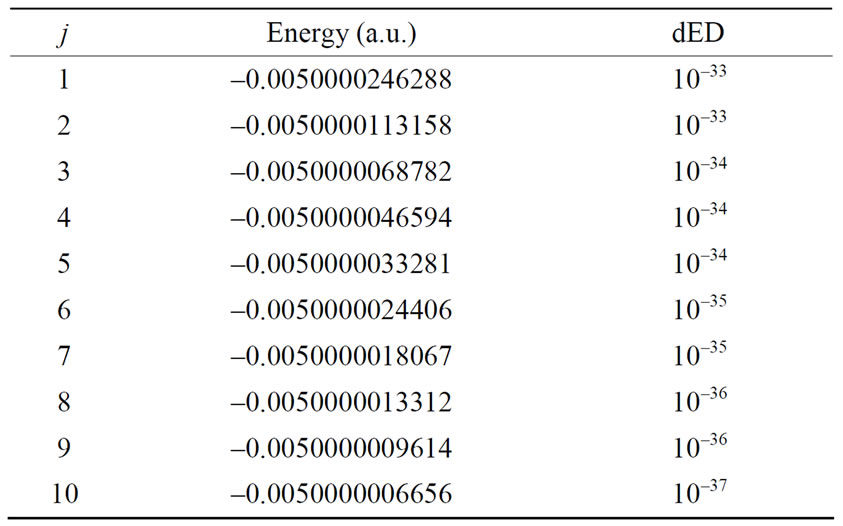
Table 2. Set of fine structures with quantum number n = 10 for atomic hydrogen.
fine structure levels for the quantum numbers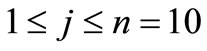 of the hydrogen atom, where we have used N = 7 and the order of precision dED was obtained after 4 iterations.
of the hydrogen atom, where we have used N = 7 and the order of precision dED was obtained after 4 iterations.
The energy levels for several hydrogen isoelectronic atoms calculated by the present theory are shown in Table 3. In this table ni is the number of iterations for a given order of precision, N is the truncation integer of the power series in Equation (3.7) and dED gives the comparative accuracy between the exact analytical Dirac solution and our numerical results. Using N = 9 to calculate the energy of Ba+55 we have obtained a precision of 10–14 against 10–31 for N = 11. In the case of U+91 we have obtained the precision of 10–9, 10–23 and 10–31 for N = 9, N = 11 and N = 15, respectively. In order to improve precision, we only have to increase the value of N in the series in Equation (3.7). We can also observe in Table 3 that when Z increases, the interaction is slower and it is necessary to increase N as well. In Table 4 we compare the results obtained by our approach with the results found in the literature. The order of precision of our results (dED), in Table 4, is 10–30. The numerical applications shown in Tables 1-4 indicates that our method has a high numerical accuracy with respect to the analytical results obtained by Dirac.
4. Conclusions
In this paper, we have shown that there is an irreducible two dimensional representation for the Dirac equation whose analytical solution generates the same set of energy eigenvalues as the usual four dimensional representation and further that it makes possible to construct a numerical method which is a mirror of the Dirac differential equationn, from what comes highly accurate approximations for the energy eigenvalues. Finally we would like to stress that the novelty our method to obtain the energy values of the Dirac-Coulomb problem derives directly from the Dirac equation, and not from the usual minimization procedures of the Dirac Hamiltonian.
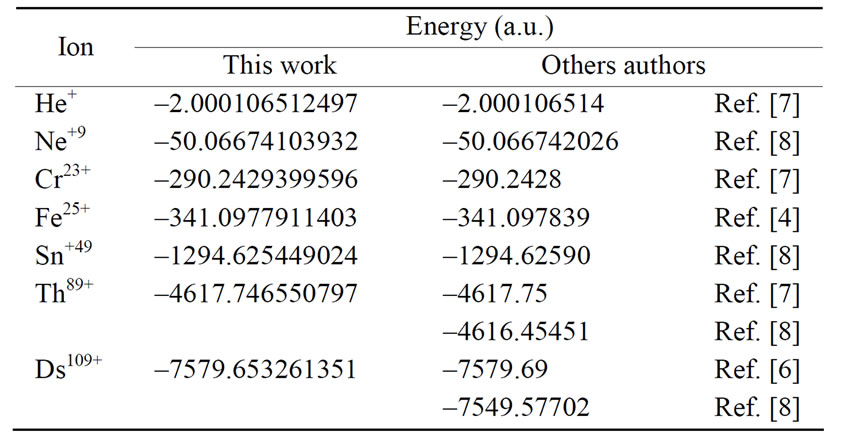
Table 4. Relativistic energy of the ground state of Hydrogenlike atoms (Z = 2, 10, 24, 26, 50, 90 and 110) results by this work and by others authors.
5. Acknowledgements
ALAF and MAA acknowledge CNPq (Brazilian agency) for a Research Grant.