Adaptive Internal Model Control of a DC Motor Drive System Using Dynamic Neural Network ()
1. Introduction
During recent decades, adaptive internal model control has been studied in several research works of which we mention [1-11]. It has been exploited in several industrial fields. It is usually interesting for its performances in servo and control where systems to be controlled are dynamic, complex, finite dimensional, open-loop stable and in addition if they have numerous delays and disruptions.
Another advantage of the structure of this control lies in its simple construction and easy interpretation of the roles of its building blocks. It includes an internal model which is an explicit process model to be controlled, a controller which can be chosen the inverse of this model and, if necessary, robustness filters.
The modeling process is to find a model whose dynamic behavior of the process approach based either on theoretical analysis, either on an experimental analysis, or on theoretical and experimental analysis. This model will be used to make predictions of the output of the process for learning the controller, and even to simulate the processes within the control system [12-16].
The inversion of model is one of the main problems of the approach of adaptive internal model control, since the direct inversion of the model for most physical systems provides an unrealizable structure (systems characterized by a function of transfer with the order of numerator less than the order of the denominator, the systems of nonminimum phase systems with delay, etc.). In this contextour work presents solutions that enable the design of a controller who comes to the best of the inverse model [17-23].
In the case of a model which is not perfect, a robust filter is useful to avoid destabilization of the command structure in the presence of modeling errors and/or major disturbances [24]. The robustness filter is usually synthesized based on the Nyquist criterion [25].The method of synthesis of this filter is based on small gain theorem [26, 27]. By cons, this filter does not affect system stability but slows down the system in the case of perfect model [28].
Thus neural network based control systems which have the desirable proprieties of nonlinear mapping, generalization and learning can offered as candidates for solution to high performance electrical drives.
Our objective is to apply a neural network adaptive control scheme to a Drive Motor system. The proposed scheme can control the speed of the considered Motor Drive system to tack the reference speed with fast and damped response.
The rest of the paper is organized as follows: In Section 2, we present a description discrete time models of the considered DC Motor Drive. The adaptive conventional internal model control scheme application of the considered system is developed in Section 3. The Section 4, provide the neural adaptive internal model control scheme to our system. The stability analysis of these two adaptive internal model control systems is developed in Section 5.A comparative study between these two control schemes is illustrated in Section 6 and a conclusion is drawn in Section 7.
2. Description of DC Motor
A DC motor can be used in a variety of industrial applications [29]. The type DC motor is characterized by the following equations [30]:
The electrical equation:
 (1)
(1)
The mechanical equation:
 (2)
(2)
The electromechanical coupling equations:
 (3)
(3)
 (4)
(4)
with:
U(t) is the armature voltage (V), 
 the back EMF (V)
the back EMF (V) , R the armature resistance
, R the armature resistance ,
, 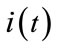 the armature current (A),
the armature current (A),  the armature inductance (H), Cm(t) the motor torque
the armature inductance (H), Cm(t) the motor torque , Cr(t) the load torque
, Cr(t) the load torque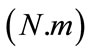 ,
,  the rotor inertia (kg·m2), f the viscous friction coefficient (N·m·s·rad–1),
the rotor inertia (kg·m2), f the viscous friction coefficient (N·m·s·rad–1),  the rotor speed (rad·s–1),
the rotor speed (rad·s–1),  the back EMF (V·s·rad–1), Km is the back torque (V·s·rad–1).
the back EMF (V·s·rad–1), Km is the back torque (V·s·rad–1).
From the above equations, the DC motor is schematically as follows (Figure 1):
with: Laplace transforms of ,
,  ,
,  and
and  are respectively
are respectively ,
,  ,
, 
 and
and ;
;  is a Laplace variable.
is a Laplace variable.
The transfer function between the input and output of the DC motor can be written as follows:
 (5)
(5)
The study of the stability of the system can be made by the Routh criterion (or Routh-Hurwitz) which is to form the following table (Table 1).
Whether 
with:
 (6)
(6)
The terms ,
,  and
and  are strictly positive so this system is stable.
are strictly positive so this system is stable.
From the Equation (5), the load torque can be consi- dered as a perturbation.
The discrete time model system can be calculated by
replacing in Equation (5)s by the approximate expression :
:
 (7)
(7)
Hence the expression of discrete system:
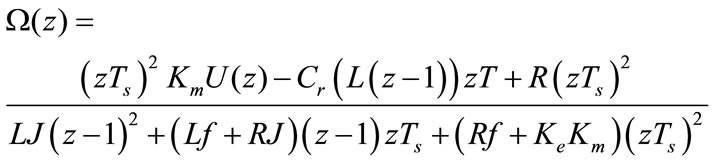 (8)
(8)
3. Adaptive Conventional Internal Model Control System of DC
The basic structure of the adaptive conventional internal model control with robustness filter of DC motor is shown in figure 2 [31].
where: 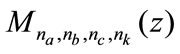 a model parameters of the process
a model parameters of the process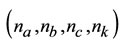 ,
,  the reference signal at instant k, y(k) the system output, C(z) the controller,
the reference signal at instant k, y(k) the system output, C(z) the controller, 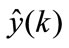 the model output,
the model output,  the difference between the reference signal and the output system,
the difference between the reference signal and the output system, 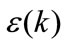 the difference between the output of the system and that of the model,
the difference between the output of the system and that of the model,  the command,
the command,  the filter robustness,
the filter robustness,  the input of the controller,
the input of the controller,  the disturbance affecting the output system such as
the disturbance affecting the output system such as .
.
The Figure 2 can be redrawn as follows (Figure 3).
For having  and robustification in the sense of stability margin, the controller, the model and the filter robustness must satisfy the following relations:
and robustification in the sense of stability margin, the controller, the model and the filter robustness must satisfy the following relations:
 (9)
(9)
 (10)
(10)
The robustness filter is often taken as first order:
 (11)
(11)
with 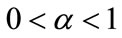

Figure 2. Basic structure of the adaptive conventional internal model control of DC motor with robustness filter.

Figure 3. Structure of adaptive conventional internal model control with robustness filter in the feedback loop.
In our work, we fix .
.
The disturbance affects both the output and system status. The model of DC motor which is of type ARMAX (Autoregressive moving average model with exogenous inputs model), is therefore given by the following equation:
 (12)
(12)
 is a noise. It can be replaced by their estimated value a priori or a posteriori:
is a noise. It can be replaced by their estimated value a priori or a posteriori:
 (13)
(13)
From Equation (12), we obtain:
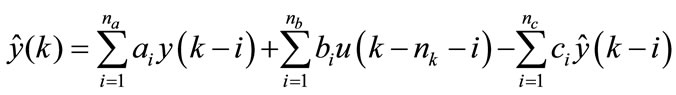 (14)
(14)
with: 
The model of the motor is as follows:
 (15)
(15)
The relations  and
and  can be written:
can be written:
 (16)
(16)
 (17)
(17)
with:  and
and  are respectively the zeros and poles of the model.
are respectively the zeros and poles of the model.
If  are less than or equal to 1, the inverse model of the system expressed by:
are less than or equal to 1, the inverse model of the system expressed by:
 (18)
(18)
This inverse model is used in adaptive conventional internal model control system replacing the  by
by . In this case, the control applied to DC motor is given by:
. In this case, the control applied to DC motor is given by:
 (19)
(19)
From the above equation, we can deduce:
 (20)
(20)
If  are strictly greater than 1 such as
are strictly greater than 1 such as , the system is unstable. One method of inversion that proposed in [32] is to partition the model into two parts: one part contains the stable zeros and the other contains the unstable zeros. In this case, the controller is chosen as the inverse of the stable part. In addition, Frank imposes a transfer equal to unity for the unstable part.
, the system is unstable. One method of inversion that proposed in [32] is to partition the model into two parts: one part contains the stable zeros and the other contains the unstable zeros. In this case, the controller is chosen as the inverse of the stable part. In addition, Frank imposes a transfer equal to unity for the unstable part.
Such as:
 (21)
(21)
So we multiply the relation (20) by  to ensure stability. Equation (20) becomes:
to ensure stability. Equation (20) becomes:
 (22)
(22)
For direct and inverse models are physically feasible, the parameters and
and  are chosen:
are chosen:
 (23)
(23)
It is possible to rewrite the Equations (14) and (19) under the following matrix forms:
 (24)
(24)
 (25)
(25)
In which the vectors of parameters and observations are defined by:
 (26)
(26)
 (27)
(27)

 (28)
(28)
The vectors of observations written yet in the forms:
 (29)
(29)
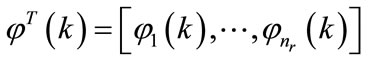 (30)
(30)
with 
The number of parameters to adjust in this command structure .
.
The adjustment procedure of the vector of model parameters 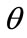 at each sampling period can be made by the parametric adaptation algorithm to minimize the following quadratic criterion:
at each sampling period can be made by the parametric adaptation algorithm to minimize the following quadratic criterion:
 (31)
(31)
This algorithm which is part of the simple gradient methods can be expressed in terms of criterion (32) as follows:
 (32)
(32)
According to [33-35], this procedure is given by the system of equations:
 (33)
(33)
 (34)
(34)
 (35)
(35)
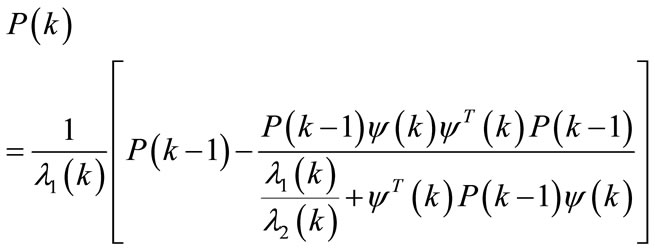 (36)
(36)
 (37)
(37)
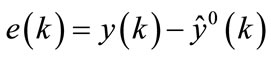 (38)
(38)
with:
 ,
,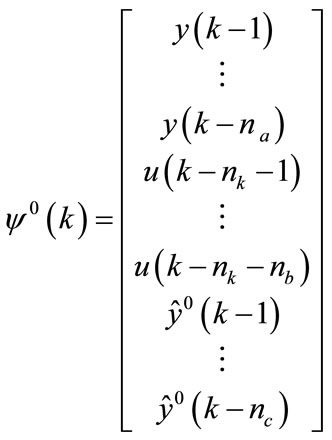 (39)
(39)
Initialization for the matrix , the parameter vector
, the parameter vector , the growth factor
, the growth factor and the decay factor
and the decay factor  is often as follows:
is often as follows:
 (40)
(40)
 (41)
(41)
 being the identity matrix of dimensions
being the identity matrix of dimensions  and
and  can be chosen equal to à
can be chosen equal to à according to Landau.
according to Landau.
 (42)
(42)
 (43)
(43)
The model output can be written as follows:
 (44)
(44)
The difference between the system output and the model output can be expressed by the Equation (45):
 (45)
(45)
The input of the equalizer is given by the following equation:
 (46)
(46)
From Equation (27), the vector of the controller parameters  estimated at time
estimated at time is defined by:
is defined by:
 (47)
(47)
The command applied to the DC motor is given by:
 (48)
(48)
The difference between the reference signal and the system output is determined by:
 (49)
(49)
4. Adaptive Neural Internal Model Control System of DC
The structures of internal model control using nonlinear neural networks have been proposed in [36-38]. The Figure 4 illustrates the structure of an adaptive neural internal model control of DC motor, where the model and the controller are replaced by recurrent neural networks with multilayer internal and external closure.
The choice of the structures of neural networks takes into account the knowledge and assumptions about the behavior of the system [39-43]. The Figures 5 and 6 present respectively the architecture of the model and the neuronal controller.
where:
 and
and 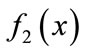 are the activation functions of neurons,
are the activation functions of neurons,
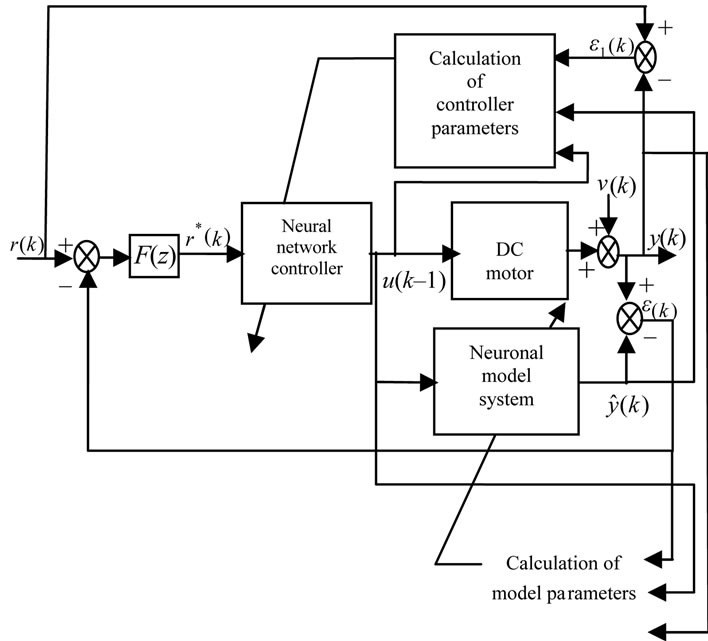
Figure 4. Basic structure of adaptive neural internal model control with filter robustness of DC motor.

Figure 6. Neural controller of the DC motor.
 the number of neurons in the hidden layer respectively of the model and controllerThe coefficients of the vector of parameters of the neural model
the number of neurons in the hidden layer respectively of the model and controllerThe coefficients of the vector of parameters of the neural model are decomposed into seven groups, formed respectively by:
are decomposed into seven groups, formed respectively by:
 the weights between neurons in the input layer and neurons in the hidden layer,
the weights between neurons in the input layer and neurons in the hidden layer,  the biases of neurons in the hidden layer,
the biases of neurons in the hidden layer,
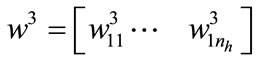 the weights between neurons in the hidden layer neurons and output layer,
the weights between neurons in the hidden layer neurons and output layer,
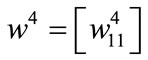 the bias of neuron in the output layer,
the bias of neuron in the output layer,
 the weights between neurons of input layer neurons and output layer,
the weights between neurons of input layer neurons and output layer,
 the weights between neurons in the hidden layer,
the weights between neurons in the hidden layer,  back weight of neuron in the output layer,
back weight of neuron in the output layer,
 the outputs of the hidden layer of neural modelThe parameters of the vector of parameters of the controller neural Wc are also broken down into seven groups, formed respectively by:
the outputs of the hidden layer of neural modelThe parameters of the vector of parameters of the controller neural Wc are also broken down into seven groups, formed respectively by:
 the weights between neurons in the input layer and neurons in the hidden layer,
the weights between neurons in the input layer and neurons in the hidden layer,
 the biases of neurons in the hidden layer,
the biases of neurons in the hidden layer,
 the Weights between neurons in the hidden layer neurons and output layer,
the Weights between neurons in the hidden layer neurons and output layer, 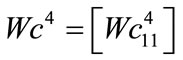 the bias of neuron in the output layer,
the bias of neuron in the output layer,  the weights between neurons of input layer neurons and output layer,
the weights between neurons of input layer neurons and output layer,
 the weights between neurons in the hidden layer,
the weights between neurons in the hidden layer,
 back weight of neuron in the output layer,
back weight of neuron in the output layer,
 the outputs of the hidden layer of neural controller.
the outputs of the hidden layer of neural controller.
The two vectors of model parameters and the neural controller are respectively the following forms:
 ,
,
 (50)
(50)
These two vectors are of size , such as
, such as
 .
.
In this section, the number of fitting parameters .
.
The output of neural model of DC motor 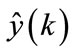 and the output of the controller neural
and the output of the controller neural  are respectively the following forms:
are respectively the following forms:
 (51)
(51)
 (52)
(52)
with:
 (53)
(53)
 (54)
(54)
 (55)
(55)
 (56)
(56)
Note by  nonlinear function representing the neuronal controller and
nonlinear function representing the neuronal controller and  nonlinear function representing the neural model of the controlled system. We can then express respectively
nonlinear function representing the neural model of the controlled system. We can then express respectively  and
and  by the following expressions:
by the following expressions:
 (57)
(57)
 (58)
(58)
The neural model is updated to minimize the error function  defined by:
defined by:
 (59)
(59)
The adjustment of the online parameter vector of this model by Levenberg-Marquardt, which belongs to the class of gradient methods of second order, is performed as follows [44-48]:
of this model by Levenberg-Marquardt, which belongs to the class of gradient methods of second order, is performed as follows [44-48]:
 (60)
(60)
such as:
 (61)
(61)
 (62)
(62)
 (63)
(63)
 (64)
(64)
 (65)
(65)
 (66)
(66)
 (67)
(67)
 (68)
(68)
The update of parameters depends on the desired performance indices (accuracy, stability). She is stopped if the number of iterations is reached or  or
or  or
or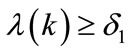 .
.
With  is the Euclidean norm.
is the Euclidean norm.
In our work, we fix 
 and
and .
.
The neural model parameters  and the learning rate
and the learning rate  must be initialized as follows:
must be initialized as follows:
The matrix elements ,
,  ,
,  ,
,  and
and  are in interval
are in interval  [48].
[48].
 and
and  .
.
 according to Bishop [49].
according to Bishop [49].
where:
I the identity matrix of size .
.
 (69)
(69)
 is a positive definite matrix and can therefore be invertible using the Cholesky method [50,51].
is a positive definite matrix and can therefore be invertible using the Cholesky method [50,51].
If all conditions are met a good identification, the model output  is then a good approximation of the output system
is then a good approximation of the output system  , which allows writing:
, which allows writing:
 (70)
(70)
 (71)
(71)
The learning of neural controller is implemented so as to minimize the following quadratic criterion:
 (72)
(72)
Using the Levenberg-Marquardt method, the vector of parameters of the controller 
 is adjusted online by the following equations:
is adjusted online by the following equations:
 (73)
(73)
 (74)
(74)
 (75)
(75)
 (76)
(76)
 (77)
(77)
 (78)
(78)
 (79)
(79)
 (80)
(80)
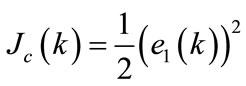 (81)
(81)
 (82)
(82)
 (83)
(83)
The online adjustment of the parameters must be repeated until such time as the number of iterations is reached or  or
or  or
or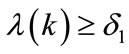 .
.
The neural controller parameters  and the positive definite matrix
and the positive definite matrix  must be initialized as follows:
must be initialized as follows:
The elements of matrices
 and
and 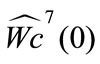 are in the interval
are in the interval .
.
 and
and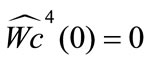 ,
, .
.
5. Stability Analysis
If the system to be controller is stable, and if its model is perfect, then the system controlled by the adaptive internal model control structure is stable if and only if the controller is stable [1,28,52]. The parametric adaptation algorithm and the Levenberg-Marquardt algorithm are algorithms stable. The neural model, neural controller and the conventional model are stable. We can therefore conclude that the control systems mentioned previously of the DC motor are stable.
6. Comparative Study
In our work, we will assume that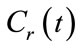 ,
,  and
and  are variable during the time (Figure 7).
are variable during the time (Figure 7).
The considered DC motor having the following characteristics:
 ,
,  ,
,  ,
,
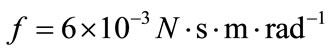 .
.
The choice of the sampling period can have a dramatic effect on the results of the identification and control. If the sampling period is chosen large enough, this causes a bad description of the dynamics of the system and can lead to failure. By cons, if the sampling period is low, then the values of some parameters may become very small, so it is difficult to estimate with good accuracy. According to [53], the sampling period  can be determined from the step response of the process. In this sense, Isermann proposed choose
can be determined from the step response of the process. In this sense, Isermann proposed choose  satisfying:
satisfying:
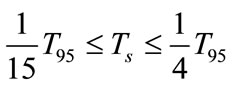 (84)
(84)
where  represents the response time to
represents the response time to  of the system.
of the system.
 (a)
(a) (b)
(b) (c)
(c)
Figure 7. DC motor parameters: (a) Load torque; (b) Back EMF; (c) Back torque.
The Figure 8 shows that:
 (85)
(85)
So:



Figure 8. Step response of DC motor: determined of the sampling period Ts.
 (86)
(86)
We fix 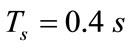
The Figure 9 shows the sequence input and output used to calculate the model parameters. These sequences
 (a)
(a) (b)
(b)
Figure 9. Sequences Data: (a) Input sequence; (b) Output sequence.
represent the system response to a random signal of zero mean and variance 1.
From Table 2, the best model to correctly approach the system dynamics model is  .
.
We fix  and
and  .
.
To validate the model chosen , we plot the autocorrelation functions of residuals (Figure 10) and cross-correlation between input and residuals (Figure 11). We note that these two functions are almost within the confidence intervals, thus validating the use of the resulting network as a model system studied.
, we plot the autocorrelation functions of residuals (Figure 10) and cross-correlation between input and residuals (Figure 11). We note that these two functions are almost within the confidence intervals, thus validating the use of the resulting network as a model system studied.
The curves representing the evolution of the model parameters are plotted in Figure 12.
The Figures 13 and 14 represent the evolutions of zeros and poles of the model. The modules of the poles and zeros of the models are less than 1, thus validating the stability of this control system.
To build the neural model of the engine, we used the

Table 2. Nash criterion values of the different candidate models.

Figure 10. Auto-correlation function of residuals.

Figure 11. Intercorrelation function between input and residuals.
data sequences that are represented in Figure 9. The evolution of the Nash criterion of different candidate models of the DC motor (Table 3) leads to the conclusion that 5 neurons in the hidden layer are necessary and sufficient for a neuronal model with satisfactory accuracy. It therefore sets  .
.
The autocorrelation functions of residuals and cross-

Figure 12. Evolution of model parameters.

Figure 13. Evolution of the zeros of the model.

Figure 14. Evolution of the poles of the model.
correlation between input and residuals (Figure 15) are within the confidence intervals, thus validating the use of the network chosen as the model system studied.

Table 3. Evolution of the Nash criterion of different neural models.
The performance of the adaptive conventional internal model control law applied to the DC motor is illustrated in Figures 16, 17 and 18. On the other side, the Figures 19, 20 and 21 show the results of adaptive neural internal model control of the DC motor. By comparing the results of two control systems of the DC motor mentioned previously, we see clearly:
- therefore the adjustment of adaptive neural internal model control system parameters requires more time than the conventional adaptive internal model control system.
therefore the adjustment of adaptive neural internal model control system parameters requires more time than the conventional adaptive internal model control system.
-A sudden change of system parameters implies a sudden change in the amplitude of the model output and the controlled system.
-The system output and the neural model output are almost identical, which confirms that the neural network is synthesized with more high precision than the output
 (a)
(a) (b)
(b)
Figure 15. Tests of model validation: (a) Autocorrelation function of residuals; (b) Intercorrelation function between input and output residuals.
model obtained by the conventional identification method.
-The control signal shows fluctuations in the case of adaptive conventional internal model control. By cons in the case of adaptive neural internal model control, fluctuations are greatly diminished.
-The output of the adaptive neural internal model control system adequately follows the reference signal compared to the output of conventional adaptive internal model control system.
-The evolutions of the criterion  clearly show that the adaptive conventional internal model control system cannot fully offset the effect of disturbance compared to the adaptive neural internal model control system.
clearly show that the adaptive conventional internal model control system cannot fully offset the effect of disturbance compared to the adaptive neural internal model control system.
7. Conclusion
In this paper, two adaptive internal model control structures are used so that the speed of DC motor follows the given trajectories.
The comparative study showed the effectiveness of the adaptive neural internal model control system compared to conventional adaptive internal model control system. Indeed, it was found that the adaptive control system by neural internal model meets the desired objectives: the powerful regulation and robustness of the speed, the disturbance rejection and system stability.
Appendixs
The model obtained from the estimation of its parameters is valid strictly used for the experiment. So check it is compatible with other forms of input in order to properly represent the system operation to identify. Most static tests of model validation are based on the criterion of Nash, on the auto-correlation of residuals, based on cross-correlation between residues and other inputs to the system. According to [54], the Nash criterion is given by the following equation:
 (87)
(87)
In our work, the number of samples N is equal to 2251.
In [55,56], the correlation functions are:
-autocorrelation function of residuals:
 (88)
(88)
-crosscorrelation function between the residuals and the previous entries:
 (89)
(89)
Ideally, if the model is validated, the results of correlation tests and the Nash criterion following results:

Typically, we verify that 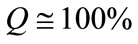 and the functions
and the functions  are null for the interval
are null for the interval  with a confidence interval
with a confidence interval , that is to say that:
, that is to say that:
 .
.
The calculation of partial derivatives is carried by the following equations:
-for the neuron in the output layer:
 (90)
(90)
 (91)
(91)
 (92)
(92)
 (93)
(93)
 (94)
(94)
 (95)
(95)
 (96)
(96)
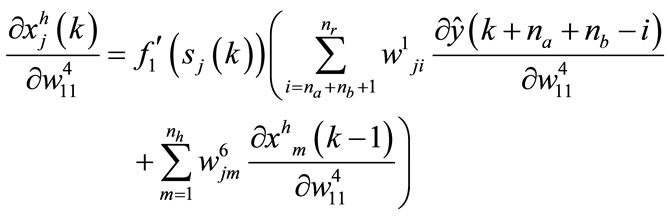 (97)
(97)
-for a neuron in the hidden layer:
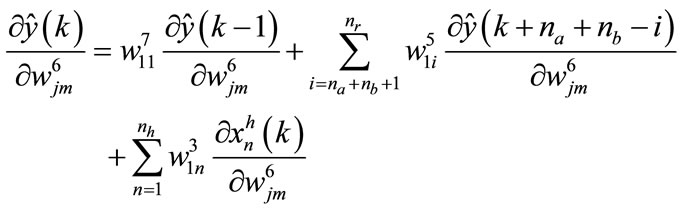 (98)
(98)

 (99)
(99)

 (100)
(100)
 (101)
(101)

 (102)
(102)

 (103)
(103)
 (104)
(104)

 (105)
(105)
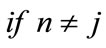
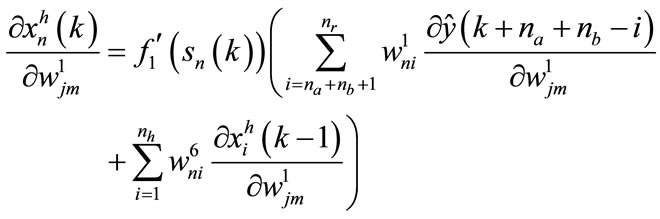 (106)
(106)
The calculation of the coefficient matrix of the network D is conducted via the two following relations [39]:
 (107)
(107)
 (108)
(108)
If we denote:
 (109)
(109)
We can write the equations (107) and (108) as follows:
 (110)
(110)
 (111)
(111)
The terms  and
and  are called the system Jacobian. They can be determined through the controller considered and the use of numerical approximation of the partial derivative:
are called the system Jacobian. They can be determined through the controller considered and the use of numerical approximation of the partial derivative:
 (112)
(112)
We have then the following approximate relations:
 (113)
(113)
 (114)
(114)
 (115)
(115)
 (116)
(116)
The Jacobiens  and
and  are calculated directly by the back-propagation of the partial derivative of output network
are calculated directly by the back-propagation of the partial derivative of output network  respectively compared to
respectively compared to
 and
and  through the neuronal controller.
through the neuronal controller.