1. Introduction
In 1942 Menger [3] introduced the notion of a probabilistic metric space (PM-space) which is in fact, a generalization of metric space. The idea in probabilistic metric space is to associate a distribution function with a point pair, say (p, q), denoted by F(p, q, t) where t > 0 and interpret this function as the probability that distance between p and q is less than t, whereas in the metric space the distance function is a single positive number. Sehgal [4] initiated the study of fixed points in probabilistic metric spaces. First, we recall that a real valued function defined on the set of real numbers is known as a distribution functions if it is non-decreasing, left continuous with inf f(x) = 0 and sup f(x) = 1. In what follows, H(x) denotes the Heavy side function, a simple example of distribution function.

Definition 1.1. A probabilistic metric space is a pair (X, F), where X is a non empty set and F is a function defined  (the set of all distribution functions) satisfying the following properties:
(the set of all distribution functions) satisfying the following properties:
1) 
2) 
3)  and 4)
and 4)  and
and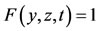 , then
, then  for all
for all  and s, t > 0.
and s, t > 0.
For each x and y in X and for each real number t > 0, F(x, y, t) is to be thought of as the probability that the distance between x and y is less than t. Of course, a metric space (X, d) induces a PM-space. Every metric space (X, d) can be realized as a probabilistic metric space by taking : defined by
: defined by 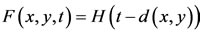 for all x, y in X.
for all x, y in X.
Definition 1.2. A t-norm (in the sense of B. Schweizer and A. Sklar [5]) 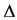 is a 2-place function
is a 2-place function  satisfying the following:
satisfying the following:
1)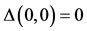
2) 
3) 
4)  and
and
5) for all
for all .
.
Definition 1.3. A Menger PM-space is a triplet (X, F, ∆) where (X, F) is a PM-space and ∆ is a t-norm with the following condition:
 for all x, y, z
for all x, y, z  X and s, t > 0.
X and s, t > 0.
This inequality is known as Menger’s triangle inequality.
Definition 1.4. A sequence {xn} in (X, F, ∆) is said to
1) Converge to a point x  X if for every ε > 0 and λ > 0, there exists a positive integer N(ε, λ) such that
X if for every ε > 0 and λ > 0, there exists a positive integer N(ε, λ) such that  for all n ³ N(ε, λ).
for all n ³ N(ε, λ).
2) Be a Cauchy sequence if for every ε > 0 and λ > 0, there exists a positive integer N(ε, λ) such that 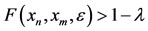 for all n, m ³ N(ε, λ).
for all n, m ³ N(ε, λ).
A Menger space (X, F, ∆) is said to be complete if every Cauchy sequence in X converges to a point in X.
In 1972, the notion of contraction mappings on probabilistic metric spaces was first introduced by Sehgal et al. [4], that is, “every contraction mapping on a complete Menger space has a unique fixed point”. Recently, Kohli and Vashistha [1] formulate the notion of R-weakly commuting mappings of type 1), R-weakly commuting mappings of type 2) and R-weakly commuting mappings of type 3) as follows:
Definition 1.5. A pair of self-mappings (f, g) of a Menger probabilistic metric space (X, F, ∆) is said to be
1) Weakly commuting if
2) R-weakly commuting if there exists some R > 0 such that
3) R-weakly commuting mappings of type 1) if there exists some R > 0 such that
4) R-weakly commuting mappings of type 2) if there exists some R > 0 such that 
5) R-weakly commuting mappings of type 3) if there exists some R > 0 such that  for all x
for all x 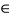 X and t > 0.
X and t > 0.
Moreover, such mappings commute at their coincidence points.
Now we state a Lemma which is useful for further study.
Lemma 1.1 [5]. Let (X, F, ∆) be a Menger space. If there exists k  (0, 1) such that
(0, 1) such that  for all x, y
for all x, y 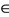 X and t > 0, then x = y.
X and t > 0, then x = y.
2. Weakly Compatible Maps
In 1982, Sessa [6], weakened the concept of commutativity to weakly commuting mappings. Afterwards, Jungck [7] enlarged the concept of weakly commuting mappings by adding the notion of compatible mappings. In 1991, Mishra [8] introduced the notion of compatible mappings in the setting of probabilistic metric space.
Definition 2.1 [8].
Let (X, F, ∆) be a Menger space such that the t-norm  is continuous and S, T be mappings from X into itself. Then, S and T are said to be compatible if
is continuous and S, T be mappings from X into itself. Then, S and T are said to be compatible if  for all t > 0, whenever {xn} is a sequence in X such that
for all t > 0, whenever {xn} is a sequence in X such that  for some
for some .
.
In 1996, Jungck [9] introduce the notion of weakly compatible mappings as follows:
Definition 2.2. Two self mappings S and T are said to be weakly compatible if they commute at their coincide points, i.e., Tu = Su for some , then TSu = STu.
, then TSu = STu.
Example 2.1. Let X = [0, 3] be equipped with the usual metric . Define
. Define  by
by

and

Then for any x  [1,3], x is a coincidence point and fgx = gfx, showing that f, g are weakly compatible maps on [0, 3].
[1,3], x is a coincidence point and fgx = gfx, showing that f, g are weakly compatible maps on [0, 3].
Remark 2.1. Every weakly compatible map need not be compatible, see Example 2.2.
Kohli and Vashistha [1] proved the following result:
Theorem 2.1. Let f and g be R-weakly commuting self mappings of a Menger probabilistic metric space (X, F, T), where T denotes a continuous t-norm, satisfying conditions
(a-I)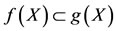
(a-II)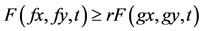 for all x, y in X, where
for all x, y in X, where  is a continuous function such that r(t) > t for each 0 < t < 1, r (0) = 0 and r (1) = 1.
is a continuous function such that r(t) > t for each 0 < t < 1, r (0) = 0 and r (1) = 1.
(a-III) If there exist sequences {xn} and {yn} in X such that ,
,  and
and , then
, then 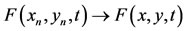 .
.
If one of the mappings f and g is continuous, then the mappings f and g have a unique common fixed point.
Remark 2.2. Recently, Mihet [10] proved that probabilistic version of Pant’s theorem holds if some addition conditions 1) Every asymptotically regular sequence in f(X) converges; 2) there exists x0 in X, x1  g–1 (fx0): F(fx0, fx1, t) > 0, for all t > 0; 3) x ≠ y implies there exists t > 0 : 0 < F(x, y, t) < 1) are imposed on the Theorems 4.7 and 4.8 of the paper [1]. The coditions 2) and 3) may be replaced by some stronger condition F(x, y; t) > 0 for all x, y in X and t > 0.
g–1 (fx0): F(fx0, fx1, t) > 0, for all t > 0; 3) x ≠ y implies there exists t > 0 : 0 < F(x, y, t) < 1) are imposed on the Theorems 4.7 and 4.8 of the paper [1]. The coditions 2) and 3) may be replaced by some stronger condition F(x, y; t) > 0 for all x, y in X and t > 0.
Now we come to our main result.
Let (X, F, ∆) be a complete Menger probabilistic metric space and  continuous t-norm. Let A, B, S and T be self-mappings of X satisfying the following conditions:
continuous t-norm. Let A, B, S and T be self-mappings of X satisfying the following conditions:
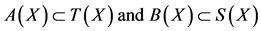 , (2.1)
, (2.1)
 (2.2.)
(2.2.)
for all x, y  X, where
X, where  is a continuous function such that
is a continuous function such that  for each 0 < s < 1 with
for each 0 < s < 1 with  .
.
Then for any arbitrary point x0  X by (2.1), we choose a point x1
X by (2.1), we choose a point x1  X such that Ax0 = Tx1 and for this point x1, there exists a point x2
X such that Ax0 = Tx1 and for this point x1, there exists a point x2  X such that Sx2 = Bx1 and so on. Continuing in this way, we can construct a sequence {yn} in X such that
X such that Sx2 = Bx1 and so on. Continuing in this way, we can construct a sequence {yn} in X such that
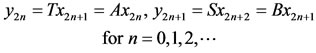 (2.3)
(2.3)
To prove our main result, firstly we prove the following lemma:
Lemma 2.1. Let A, B, S and T be self-mappings of a Menger probabilistic metric space (X, F, ∆), and
 continuous t-norm, satisfying the conditions (2.1) and (2.2). Then the sequence {yn} defined by (2.3) is a Cauchy sequence in X.
continuous t-norm, satisfying the conditions (2.1) and (2.2). Then the sequence {yn} defined by (2.3) is a Cauchy sequence in X.
Proof. For t > 0,
 (2.4)
(2.4)
as  for 0 < s < 1. Thus
for 0 < s < 1. Thus
 is an increasing sequence of positive real numbers in [0, 1] and therefore tends to a limit l ≤ 1. We assert that l = 1. If not, l < 1 which on letting
is an increasing sequence of positive real numbers in [0, 1] and therefore tends to a limit l ≤ 1. We assert that l = 1. If not, l < 1 which on letting  in (2.4), one gets
in (2.4), one gets  a contradiction yielding thereby l = 1. Therefore for every n
a contradiction yielding thereby l = 1. Therefore for every n  Nusing analogous arguments one can show that
Nusing analogous arguments one can show that
 is a sequence of positive real numbers in [0, 1] which tends to a limit l = 1. Therefore for every n
is a sequence of positive real numbers in [0, 1] which tends to a limit l = 1. Therefore for every n  N,
N,  and
and
 . Now for any positive integer p, we obtain,
. Now for any positive integer p, we obtain,

Since  for t > 0, it follows that
for t > 0, it follows that  which shows that {yn} is a Cauchy sequence in X.
which shows that {yn} is a Cauchy sequence in X.
Now we come to our main result.
Theorem 2.2. Let A, B, S and T be four self-mappings of a Menger space (X, F, ∆) satisfying the conditions (2.1) and (2.2) and one of A(X), B(X), S(X) and T(X) is a complete subspace of X, then 1) A and S have a point of coincidence2) B and T have a point of coincidence.
Moreover, if the pairs (A, S) and (B, T) are weakly compatible, then A, B, S and T have a unique common fixed point.
Proof. Let x0 be an arbitrary point in X. Then from (2.3), we have y2n = Tx2n + 1 = Ax2n and y2n + 1 = Sx2n + 2 = Bx2n + 1. Then due to Lemma 2.1, {yn} is a Cauchy sequence in X. Now suppose that S(X) is a complete subspace of X, then the subsequence y2n + 1 = Sx2n+2 must get a limit in S(X). Call it to be u and v  S−1u. Then Sv = u. As {yn} is a Cauchy sequence containing a convergent subsequence {y2n+1}, therefore the sequence {yn} also converges implying thereby the convergence of {y2n} being a subsequence of the convergent sequence {yn}.
S−1u. Then Sv = u. As {yn} is a Cauchy sequence containing a convergent subsequence {y2n+1}, therefore the sequence {yn} also converges implying thereby the convergence of {y2n} being a subsequence of the convergent sequence {yn}.
On setting x = v and y = x2n+1 in (2.2) one gets (for t > 0),
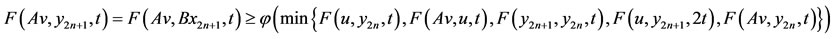
which on letting  reduces to
reduces to
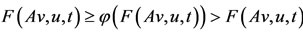 a contradiction. Therefore Av = u = Sv, which shows that the pair (A, S) has a point of coincidence. As
a contradiction. Therefore Av = u = Sv, which shows that the pair (A, S) has a point of coincidence. As  , Av = u implies that
, Av = u implies that . Let w
. Let w  T−1u, then Tw = u. On setting x = x2n and y = w in (2.2) one gets (for t > 0),
T−1u, then Tw = u. On setting x = x2n and y = w in (2.2) one gets (for t > 0),

which on letting  reduces to
reduces to
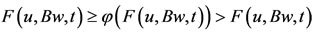 , a contradiction. Therefore u = Bw. Thus we have shown u = Av = Sv = Bw = Tw which amounts to say that both pairs have point of coincidence. If one assumes T(X) to be complete, then an analogous argument establishes this claim.
, a contradiction. Therefore u = Bw. Thus we have shown u = Av = Sv = Bw = Tw which amounts to say that both pairs have point of coincidence. If one assumes T(X) to be complete, then an analogous argument establishes this claim.
The remaining two cases pertain essentially to the previous cases. Indeed if  is complete, then
is complete, then  and if
and if  is complete, then
is complete, then  . Thus 1) and 2) are completely established. Since the pairs (A, S) and (B, T) are weakly compatible and v and w are their points of coincidence respectively, then Au = A(Sv) = S(Av) = Su and Bu = B(Tw) = T(Bw) = Tu.
. Thus 1) and 2) are completely established. Since the pairs (A, S) and (B, T) are weakly compatible and v and w are their points of coincidence respectively, then Au = A(Sv) = S(Av) = Su and Bu = B(Tw) = T(Bw) = Tu.
If , then on setting x = u and y = w in (2.2), one gets (for t > 0),
, then on setting x = u and y = w in (2.2), one gets (for t > 0),

a contradiction. Therefore Au = u. Similarly, one can show that Bu = u. Thus u is a common fixed point of A, B, S and T. The uniqueness of a common fixed point follows easily. Also u remains the unique common fixed point of both pairs separately. This completes the proof.
Example 2.2. Let A, B, S and T be self maps on Menger probabilistic metric space X = [0, 1] with usual metric d defined by . For each
. For each define
define 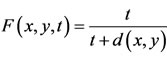 and
and , for all x, y
, for all x, y  X. Then (X, F, ∆) is a Menger probabilistic metric space, where ∆ is defined by
X. Then (X, F, ∆) is a Menger probabilistic metric space, where ∆ is defined by . Define A, B, S, T:
. Define A, B, S, T:  by
by


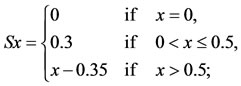

and define  as
as ,
,  and
and
 for 0 < s < 1. If we take k = 0.5 and t = 1, then we see that A, B, S and T satisfy all the conditions of the above theorem and have a unique common fixed point
for 0 < s < 1. If we take k = 0.5 and t = 1, then we see that A, B, S and T satisfy all the conditions of the above theorem and have a unique common fixed point . We note that the mappings A and S commute at the coincidence point
. We note that the mappings A and S commute at the coincidence point , and hence A and S are weakly compatible maps. Similarly B and T are weakly compatible maps. To see that the pairs {A, S} and {B, T} are non compatible, let us consider a decreasing sequence {xn} such that xn
, and hence A and S are weakly compatible maps. Similarly B and T are weakly compatible maps. To see that the pairs {A, S} and {B, T} are non compatible, let us consider a decreasing sequence {xn} such that xn 0.5. Then Axn
0.5. Then Axn 0.15, Sxn
0.15, Sxn 0.15, but
0.15, but
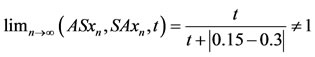 .
.
Thus the pair (A, S) is non compatible. Also Bxn 0.35, Txn
0.35, Txn 0.35 but
0.35 but
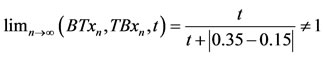 .
.
Hence, the pair (B, T) is non compatible. All the mappings involved in this example are discontinuous at the common fixed point.
Theorem 2.3. Theorem 2.2 remains true if a “weakly compatible” property is replaced by any one (retaining the rest of the hypotheses) of the following:
1) R-weakly commuting property,
2) R-weakly commuting property of type 2),
3) R-weakly commuting property of type 1),
4) R-weakly commuting property of type 3),
5) weakly commuting property.
Proof. Since all the conditions of Theorem 2.2 are satisfied, then the existence of coincidence points for both the pairs is insured. Let x be an arbitrary point of coincidence for the pair (A, S), then using R-weak commutativity one gets , which amounts to say that ASx = SAx. Thus the pair (A, S) is coincidentally commuting. Similarly (B, T) commutes at all of its coincidence points. Now applying Theorem 2.2, one concludes that A, B, S and T have a unique common fixed point. In case (A, S) is an R-weakly commuting pair of type 2), then
, which amounts to say that ASx = SAx. Thus the pair (A, S) is coincidentally commuting. Similarly (B, T) commutes at all of its coincidence points. Now applying Theorem 2.2, one concludes that A, B, S and T have a unique common fixed point. In case (A, S) is an R-weakly commuting pair of type 2), then , which amounts to say that ASx = S2x. Now,
, which amounts to say that ASx = S2x. Now,

which gives contradiction, yielding thereby ASx = SAx. Similarly, if pair is R-weakly commuting mappings of type 1) or type 3) or weakly commuting, then (A, S) also commutes at their points of coincidence. Similarly, one can show that the pair (B, T) is also weakly compatible. Now in view of Theorem 2.2, in all four cases A, B, S and T have a unique common fixed point. This completes the proof.
3. Property (E.A.)
Recently, Amari and Moutawakil [11] introduced a generalization of non compatible maps as property (E.A.).
Definition 3.1. Let A and S be two self-maps of a metric space (X, d). The pair (A, S) is said to satisfy property (E.A.), if there exists a sequence {xn} in X such that
 , for some
, for some .
.
Now in a similar mode we state property (E.A.) in Menger probabilistic metric spaces.
Definition 3.2. A pair of self-mappings (f, g) of a Menger probabilistic metric space (X, F, ∆) is said to satisfy property(E.A.), if there exists a sequence {xn} in X such that , for some
, for some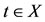 .
.
Example 3.1 [11]. Let . Define
. Define
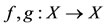 by
by  and
and , for all x in X. Consider the sequence
, for all x in X. Consider the sequence . Cleary
. Cleary
 . Then f and g satisfy property (E.A.).
. Then f and g satisfy property (E.A.).
Example 3.2 [11]. Let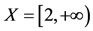 . Define
. Define  by gx = x + 1 and fx = 2x + 1, for all x
by gx = x + 1 and fx = 2x + 1, for all x  X. Suppose that the property (E.A.) holds. Then, there exists a sequence {xn} in X satisfying
X. Suppose that the property (E.A.) holds. Then, there exists a sequence {xn} in X satisfying
 for some z
for some z  X. Therefore,
X. Therefore,  and
and . Thus, z = 1which is a contradiction, since 1 is not contained in X. Hence f and g do not satisfy property (E.A.).
. Thus, z = 1which is a contradiction, since 1 is not contained in X. Hence f and g do not satisfy property (E.A.).
Example 3.3 [12]. Let (X, F, ∆) be a Menger probabilistic metric space, where X = [0, 2] with minimum tnorm, and  for all t > 0 and for all x, y
for all t > 0 and for all x, y  X. Define the self maps f and g as follows:
X. Define the self maps f and g as follows:


Let  is a sequence in X such that
is a sequence in X such that  . By definition of f and g, we have z
. By definition of f and g, we have z  {1}. Thus {f, g} satisfies property (E.A.). Two selfmappings S and T of a Menger space (X, F, t) will be noncompatible if there exists at least one sequence {xn} in X such that
{1}. Thus {f, g} satisfies property (E.A.). Two selfmappings S and T of a Menger space (X, F, t) will be noncompatible if there exists at least one sequence {xn} in X such that  for some z
for some z  X, but
X, but  is either not equal to 1 or non-existent. We note that noncompatible selfmappings of a Menger space (X, F, ∆) satisfy the property (E.A.).
is either not equal to 1 or non-existent. We note that noncompatible selfmappings of a Menger space (X, F, ∆) satisfy the property (E.A.).
Definition 3.3 [13]. Two pairs (A, S) and (B, T) of self mappings of a Menger PM space (X, F, ∆) are said to satisfy the common property E.A. if there exist two sequences {xn}, {yn} in X and some t in X such that
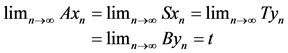
Example 3.4 [13]. Let (X, F, ∆) be Menger space with X = [−1, 1] and

for all x, y  X. Define self mappings A, B, S and T on X as
X. Define self mappings A, B, S and T on X as ,
,  ,
,  and
and  for all x
for all x  X. Taking sequences
X. Taking sequences  and
and  in X, then
in X, then
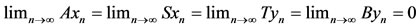 .
.
Thus, the pairs (A, S) and (B, T) share the common property (E.A.).
Now we prove the results of Kohli and Vashistha [1] for weakly compatible maps along with property (E.A.) as follows:
Theorem 3.1. Let f and g be weakly compatible self maps of a Menger probabilistic metric space (X, F, ∆) with continuous t-norm ∆ satisfying F(x, y, t) > 0 for all x, y in X and t > 0 such that conditions (a-II) and (a-III) and the following holds:
(a-IV) f and g satisfy the property (E.A.)(a-V) g(X) is a closed subspace of X.
Then f and g have a unique common fixed point in X provided f and g are weakly compatible maps.
Proof. Since f and g satisfy the property (E.A.) therefore, there exists a sequence {xn} in X such that  . As g(X) is a closed subspace of X, therefore every convergent sequence of points of g(X) has a limit point in g(X). Therefore,
. As g(X) is a closed subspace of X, therefore every convergent sequence of points of g(X) has a limit point in g(X). Therefore,  , for some
, for some . This implies
. This implies . Now we show that fa = ga. From (a-II), we have,
. Now we show that fa = ga. From (a-II), we have, . Proceeding limit as
. Proceeding limit as , we have,
, we have,
 this implies that u = ga = fa. Thus a is the coincidence point of f and g. Since f and g are weakly compatible, therefore, fu = fga = gfa = gu. Now we show that fu = u. From (a-II), we have,
this implies that u = ga = fa. Thus a is the coincidence point of f and g. Since f and g are weakly compatible, therefore, fu = fga = gfa = gu. Now we show that fu = u. From (a-II), we have, 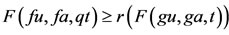 , which in turns implies that fu = u. Hence u is the unique common fixed point of f and g. Uniqueness follows easily from (a-II).
, which in turns implies that fu = u. Hence u is the unique common fixed point of f and g. Uniqueness follows easily from (a-II).
Remark 3.1. It was pointed out in [14] that a pair of maps enjoying property (E.A.) relaxes the required containment of range of one mapping into the range of other which is utilized to construct the sequence of joint iterates. Moreover, it buys containment of ranges without any continuity requirements besides minimizes the commutativity conditions of the maps to the commutativity at their points of coincidence and it also allows replacing the completeness requirement of the space with a more natural condition of closeness of the range.
Example 3.5. [14] Consider  with the usual metric. Define the self-mappings T and I on X as follows:
with the usual metric. Define the self-mappings T and I on X as follows:


Consider the sequence . Clearly,
. Clearly,
 . Then T and I satisfy property (E.A.). Also,
. Then T and I satisfy property (E.A.). Also,  and
and
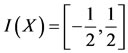 . Here one needs to note that neither T(X) is contained in I(X) nor I(X) is contained in T(X).
. Here one needs to note that neither T(X) is contained in I(X) nor I(X) is contained in T(X).
Now we prove existence of common fixed points for pairs of weakly compatible maps along with property (E. A.) using different types of control functions:
 : Consider the mapping
: Consider the mapping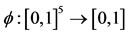 , which is upper semi-continuous, nondecreasing in each co-ordinate variable and such that
, which is upper semi-continuous, nondecreasing in each co-ordinate variable and such that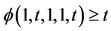 ,
,  ,
, 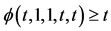 ,
, .
.
Theorem 3.2. Let A, B, S and T be self maps of a Menger probabilistic metric space (X, F, ∆) with continuous t-norm satisfying the following conditions:
1) 2)
2) 

for all x, y in X and t > 0, where 3) pairs (A, S) or (B, T) satisfy property(E.A.)4) pairs (A, S) and (B, T) are weakly compatible.
3) pairs (A, S) or (B, T) satisfy property(E.A.)4) pairs (A, S) and (B, T) are weakly compatible.
If the range of one of A, B, S and T is a closed subset of X, then A, B, S and T have a unique common fixed point in X.
Proof. Suppose that (B, T) satisfies the property (E.A.). Then there exists a sequence {xn} in X such that  for some z
for some z  X. Since
X. Since 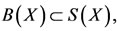 therefore, there exists a sequence {yn}
therefore, there exists a sequence {yn}  X such that
X such that . Hence
. Hence 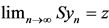 . Now we shall show that
. Now we shall show that . We claim that
. We claim that  .
.
For this we have from 2),

Proceeding limit as , we have ,
, we have ,
 , using
, using  and by Lemma 1.1, we have l = z. Therefore,
and by Lemma 1.1, we have l = z. Therefore, . Suppose that S(X) is a closed subspace of X. Then z = Su for some
. Suppose that S(X) is a closed subspace of X. Then z = Su for some  . Subsequently, we have
. Subsequently, we have

Now, we shall show that Au = z. From 2) we have ,

Letting limit as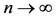 ,
,

using  and by Lemma 1.1, we have Au = Su = z. Since
and by Lemma 1.1, we have Au = Su = z. Since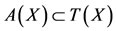 , so there exists
, so there exists  such that z = Au = Tv. Now, we claim that z = Tv = Bv. Then From 2) we have,
such that z = Au = Tv. Now, we claim that z = Tv = Bv. Then From 2) we have,
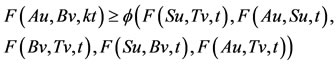
using  and by Lemma 1.1, we have z = Bv. Thus we have Au = Su = Tv = Bv = z. Since the pair (A, S) is weak compatible which implies ASu = SAu, i.e, Az = Sz.
and by Lemma 1.1, we have z = Bv. Thus we have Au = Su = Tv = Bv = z. Since the pair (A, S) is weak compatible which implies ASu = SAu, i.e, Az = Sz.
Now we show that Az = z.

Using  and by Lemma 1.1, Az = Sz = z. The weak compatibility of B and T implies that BTv = TBv, i.e., Bz = Tz. Now we shall show that z is the common fixed point of B and T. From 2), one obtain,
and by Lemma 1.1, Az = Sz = z. The weak compatibility of B and T implies that BTv = TBv, i.e., Bz = Tz. Now we shall show that z is the common fixed point of B and T. From 2), one obtain,

using 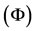 and by Lemma 1.1, Bz = z. Hence Az = Bz = Sz = Tz = z and z is a common fixed point of A, B, S and T.
and by Lemma 1.1, Bz = z. Hence Az = Bz = Sz = Tz = z and z is a common fixed point of A, B, S and T.
Example 3.6. Let X = [0, 2] equipped with the Euclidian distance and let (X, F, ∆) be the standard Menger probabilistic metric spaces induced by (X, d), i.e.,
 . Define A, B, S and T by,
. Define A, B, S and T by,


Let  be
be  and
and
 and consider
and consider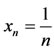 . Then,
. Then,

Hence pairs (A, S) and (B, T) share property (E.A.). Also A(X) = T(X) = {0, 1} and B(X) = S(X) = {0, 2} are a closed subset of X. Moreover, pairs (A, S) and (B, T) are weakly compatible. Thus all the conditions of the above theorem are satisfied and 0 is the unique common fixed point of A, B, S and T.
In 2008, Kubiaczyk and Sharma [2] proved the following fixed point theorem.
Corollary 3.1 [2]. Let A, B, S and T be self maps of a Menger probabilistic metric space (X, F, ∆) with continuous t-norm satisfying 1), 3), 4) and the following:
5) 

for all x, y in X and t > 0, where . If the range of one of A, B, S and T is a closed subset of X, then A, B, S and T have a unique common fixed point in X.
. If the range of one of A, B, S and T is a closed subset of X, then A, B, S and T have a unique common fixed point in X.
Proof. Set  in Theorem 3.2.
in Theorem 3.2.
Next we consider a function:
(*) satisfying the conditions:
satisfying the conditions:
 is continuous and nondecreasing on [0, 1] and
is continuous and nondecreasing on [0, 1] and  for all t in (0, 1). We note that
for all t in (0, 1). We note that  and
and  for all t in [0, 1], i.e.,
for all t in [0, 1], i.e.,  holds for every t > 0 and for all x, y in X.
holds for every t > 0 and for all x, y in X.
Theorem 3.3. Let A, B, S and T be self maps of a Menger probabilistic metric space (X, F, ∆) with continuous t-norm satisfying 1), 3), 4) and the following:
6) 

with F(x, y, t) > 0 and 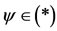 for all x, y in X and t > 0. If the range of one of A, B, S and T is a closed subset of X, then A, B, S and T have a unique common fixed point in X.
for all x, y in X and t > 0. If the range of one of A, B, S and T is a closed subset of X, then A, B, S and T have a unique common fixed point in X.
Proof. Suppose that (B, T) satisfies the property (E.A.). Then there exists a sequence {xn} in X such that  for some
for some  . Since,
. Since,
 there exists a sequence {yn}
there exists a sequence {yn}  X such that
X such that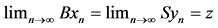 . Hence
. Hence  . We shall show that
. We shall show that . From 6) we have,
. From 6) we have,

Proceeding limit as  and using (*) one obtain,
and using (*) one obtain,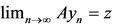 . Suppose that S(X) is a closed subspace of X. Then z = Su for some
. Suppose that S(X) is a closed subspace of X. Then z = Su for some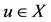 . Subsequently we have,
. Subsequently we have,

Now, we shall show that Au = Su. From 6) we have,

Letting limit as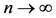 , we get,
, we get,

using (*), we have, Au = Su = z. Since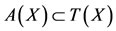 , so there exists
, so there exists 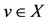 such that z = Au = Tv. Now, we claim that z = Tv = Bv. From 6) we have,
such that z = Au = Tv. Now, we claim that z = Tv = Bv. From 6) we have,
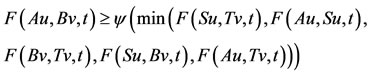
using (*), we have, z = Bv. Thus we have Au = Su = Tv = Bv = z. Since the pair (A, S) is weak compatible which implies ASu = SAu, i.e, Az = Sz. From 6), we have,

using (*), we have, Az = Sz = z. The weak compatibility of B and T implies that BTv = TBv, i.e., Bz = Tz. Now we shall show that z is the common fixed point of A, B, T and S. Suppose that . Then using 6) one obtain,
. Then using 6) one obtain,

using (*), we have, Bz = z. Hence Az = Bz = Sz = Tz = z and z is a common fixed point of A, B, S and T. Uniqueness follows easily.
Theorem 3.4. Let A, B, S and T be self maps of a Menger probabilistic metric space (X, F, ∆) with continuous t-norm satisfying 1), 2), 6) and the the following condition:
7) Pairs (A, S) and (B, T) satisfy a common property (E.A.).
If the range of S and T is a closed subset of X, then A, B, S and T have a unique common fixed point in X.
Proof. Suppose that (A, S) and (B, T) satisfy a common property(E.A.). Then there exists a sequences {xn} and {yn} in X such that

for some . Since S(X) and T(X) are closed subsets of X, we obtain z = Su = Tv for some u, v in X. From 6),
. Since S(X) and T(X) are closed subsets of X, we obtain z = Su = Tv for some u, v in X. From 6),

Letting  and using (*), we have, z = Au = Su = Tv.
and using (*), we have, z = Au = Su = Tv.
The rest of the proof follows from the above theorem.
4. Occasionally Weakly Compatible Mappings
In 2008, Al-Thagafi and Naseer Shahzad [15] introduced the concept of occasionally weakly compatible mappings.
Definition 4.1. Let A and T be selfmaps of a set X. If Ax = Tx = w (say), 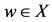 , for some x in X, then x is called a coincidence point of A and T and the set of coincidence points of A and T in X is denoted by c(A, T), w is called a point of coincidence of A and T.
, for some x in X, then x is called a coincidence point of A and T and the set of coincidence points of A and T in X is denoted by c(A, T), w is called a point of coincidence of A and T.
Definition 4.2. Two self-maps f and g of a set X are occasionally weakly compatible (shortly owc) iff there is a point x in X which is a coincidence point of f and g at which f and g commute.
Al-Thagafi and Naseer Shahzad [15] shown that occasionally weakly is weakly compatible but converse is not true.
Example 4.1. [15] Let R be the usual metric space. Define  by Sx = 2x and Tx = x2 for all
by Sx = 2x and Tx = x2 for all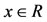 . Then Sx = Tx for x = 0, 2 but ST0 = TS0, and
. Then Sx = Tx for x = 0, 2 but ST0 = TS0, and . S and T are occasionally weakly compatible self maps but not weakly compatible.
. S and T are occasionally weakly compatible self maps but not weakly compatible.
Remark 4.1. 1) Every pair of noncompatible selfmaps of a metric space (X, d) satisfies property E.A., but its converse need not be true [16].
2) Weak compatibility and property E.A. are independent of each other [17].
3) Every compatible pair is weakly compatible but its converse need not be true [18].
4) Every weakly compatible pair is occasionally weakly compatible but its converse need not be true [19].
5) Occasionally weak compatibility and property E.A. are independent of each other [20].
Lemma 4.1 [21]. Let X be a set and f, g are owc self maps of X. If f and g have a unique point of coincidence, w = fx = gx, then w is the unique common fixed point of f and g.
Proposition 4.1. Let A, B, S and T be self maps of a Menger probabilistic metric space (X, F, ∆) with continuous t-norm satisfying (2.2) and the following conditions:
1)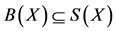 , the pair (B, T) satisfies property (E.A.) and
, the pair (B, T) satisfies property (E.A.) and  is a closed subspace of X; or
is a closed subspace of X; or
2) , the pair (A, S) satisfies property(E.A.) and
, the pair (A, S) satisfies property(E.A.) and 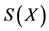 is a closed subspace of X, holds.
is a closed subspace of X, holds.
Then  and
and .
.
Proof: Suppose 1) holds.
Since the pair (B, T) satisfies property (E.A.), then there exists a sequence {xn} in X such that
 for some
for some  . Since
. Since  there exists a sequence {yn}
there exists a sequence {yn}  X such that
X such that . Now we claim that
. Now we claim that , for this purpose, suppose
, for this purpose, suppose  . Now put x = yn, and y = xn in (2.2), we have,
. Now put x = yn, and y = xn in (2.2), we have,

Letting , we have,
, we have,

Case 1. 
Case 2. , a contradiction. Hence, p = z, i.e.,
, a contradiction. Hence, p = z, i.e.,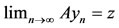 . Since T(X) is a closed subspace of X, therefore
. Since T(X) is a closed subspace of X, therefore  and this implies z = Tv for some
and this implies z = Tv for some 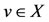 . If
. If , then on putting x = yn and y = v in (2.2), we have,
, then on putting x = yn and y = v in (2.2), we have,

Letting , we have,
, we have,

Case 1. 
Case 2.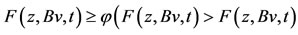 a contradiction. Hence, Bv = z = Tv, therefore
a contradiction. Hence, Bv = z = Tv, therefore  .
.
Now, since  and
and , there exists a
, there exists a  such that z = Su.
such that z = Su.
If,  , then on putting x = u and y = v in (2.2), we have,
, then on putting x = u and y = v in (2.2), we have,

i.e., 
Case 1. 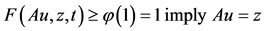
Case 2. , a contradiction. Hence, Au = z = Su.
, a contradiction. Hence, Au = z = Su.
Thus .
.
Similarly, the assertion holds under assumption 2).
Hence, Proposition 4.1 follows.
Theorem 4.1. In addition to hypothesis of Proposition 4.1 on A, B, S and T, if both the pairs (A, S) and (B, T) are owc on X, then the maps A, B, S and T have a unique common fixed point in X.
Proof: By Proposition 4.1,  , and
, and  . Since the pair (A, S) is owc, therefore there exists
. Since the pair (A, S) is owc, therefore there exists 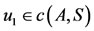 such that Au1 = Su1 = z1 (say) and ASu1 = SAu1, therefore Az1 = Sz1 = z2 (say). Since the pair (B, T) is owc, therefore there exists
such that Au1 = Su1 = z1 (say) and ASu1 = SAu1, therefore Az1 = Sz1 = z2 (say). Since the pair (B, T) is owc, therefore there exists  such that Bv1 = Tv1 = w (say) and BTv1 = TBv1, i.e., Bw = Tw = w1 (say). Next we claim that z2 = w1. If
such that Bv1 = Tv1 = w (say) and BTv1 = TBv1, i.e., Bw = Tw = w1 (say). Next we claim that z2 = w1. If , then form (2.2), we have,
, then form (2.2), we have,

imply z2 = w1. Therefore, we have Az1 = Sz1 = w1. Next we show that z1 = w1, form (2.2), we have,

imply that w1 = z1. Thus Az1 = Sz1 = z1 and Bw = Tw = z1. Next we claim that w = z1. If , then from (2.2), we have,
, then from (2.2), we have,

Imply w = z1. Hence we have Bz1 = Tz1 = z1. Therefore, we obtain Az1 = Tz1 = Bz1 = Sz1 = z1.
Uniqueness follows easily.
Example 4.2. Let X = [0, 2] equipped with the Euclidian distance and the Menger spaces induced by (X, d), i.e.,
 . Clearly (X, F, ∆) is a Menger space with
. Clearly (X, F, ∆) is a Menger space with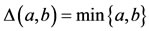 . Define the self maps A, B, S and T on X by
. Define the self maps A, B, S and T on X by




Now

and taking  for 0 < t < 1. We observe that
for 0 < t < 1. We observe that , T(X) is a closed subset of X, and neither
, T(X) is a closed subset of X, and neither 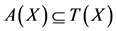 nor
nor . The selfmaps A, B, S and T satisfy the inequality (2.2). Let us consider the sequence
. The selfmaps A, B, S and T satisfy the inequality (2.2). Let us consider the sequence  Then
Then ,
,
 ,
,




 .
.
One can see that  so that the pair (B, T) satisfies property (E.A.). But the pair (B, T) is not compatible for
so that the pair (B, T) satisfies property (E.A.). But the pair (B, T) is not compatible for  Clearly, the pairs (A, S) and (B, T) are owc. Hence, the selfmaps A, B, S, and T satisfy all the conditions of Theorem 4.1 and 0 the unique common fixed point of A, B, S and T. Moreover, A, B, S and T are discontinuous at the fixed point 0.
Clearly, the pairs (A, S) and (B, T) are owc. Hence, the selfmaps A, B, S, and T satisfy all the conditions of Theorem 4.1 and 0 the unique common fixed point of A, B, S and T. Moreover, A, B, S and T are discontinuous at the fixed point 0.
Theorem 4.2. Let (X, F, ∆) be a complete Menger space and let A, B, S and T be self-mappings of X. Let the pairs (A, S) and (B, T) be owc and for  such that
such that
3) 
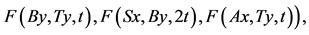
for all  and for all t > 0, then there exists a unique point
and for all t > 0, then there exists a unique point  such that Aw = Sw = w and a unique point
such that Aw = Sw = w and a unique point  such that Bz = Tz = z. Moreover, z = w, so that there is a unique common fixed point of A, B, S and T.
such that Bz = Tz = z. Moreover, z = w, so that there is a unique common fixed point of A, B, S and T.
Proof: Since the pairs (A, S) and (B, T) are owc, so there exists  such that Ax = Sx and By = Ty. We claim that Ax = By. If
such that Ax = Sx and By = Ty. We claim that Ax = By. If , then by 3),
, then by 3),

Then by Lemma 1.1, we have, Ax = By, i.e., Ax = Sx = By = Ty. Suppose that there is another point z such that Az = Sz, then by 3) Az = Sz = By = Ty. So, Ax = Az and w = Ax = Sx is the unique point of coincidence of A and S. By Lemma 4.1, w is the only common fixed point of A and S. Similarly, there is a unique point z  X such that z = Bz = Tz. Assume that
X such that z = Bz = Tz. Assume that , then by 3), we have,
, then by 3), we have,

In view of Lemma 1.1, we have z = w and z is a common fixed point of A, B, S and T.
Uniqueness follows easily from 3).
Theorem 4.3. Let (X, F, ∆) be a complete Menger space and let A, B, S and T be self-mappings of X. Let the pairs (A, S) and (B, T) be owc and for  such that
such that
4) 

for all  and
and  such that
such that
 for all 0 < t < 1, then there exists a unique common fixed point of A, B, S and T.
for all 0 < t < 1, then there exists a unique common fixed point of A, B, S and T.
Proof: Since the pairs (A, S) and (B, T) are owc, there are points  such that Ax = Sx and By = Ty. We claim that Ax = By. If not then by 4)
such that Ax = Sx and By = Ty. We claim that Ax = By. If not then by 4)

a contradiction, therefore Ax = By, i.e., Ax = Sx = By = Ty and rest of the proof follows from Theorem 4.2 by replacing inequality 3) with 4).
Corollary 4.1. Let (X, F, ∆) be a complete Menger space and let A, B, S and T be self-mappings of X. Let the pairs (A, S) and (B, T) be owc. If there exists a point  for all
for all  and t > 0, such that
and t > 0, such that
5) ,
,
then there exists a unique common fixed point of A, B, S and T.
Proof: The proof follows from Theorem 4.2.
Theorem 4.4. Let (X, F, ∆) be a complete Menger space. Then continuous self mappings S and T of X have a common fixed point in X if and only if there exists a self mapping A of X such that the following conditions are satisfied.
6) 
7) The pairs (A, S) and (A, T) are weakly compatible
8) There exists a point  for all
for all  and t > 0, such that
and t > 0, such that

Then A, S and T have a unique common fixed point.
Proof: Since weakly compatible implies owc, the result follows from Theorem 4.2.
Theorem 4.5. Let (X, F, ∆) be a complete Menger space and let A and S be self-mappings of X. Let the pair (A, S) be owc. If there exists a point  for all
for all  and t > 0, such that
and t > 0, such that
9) 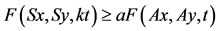

where a, b > 0, a + b > 1. Then A and S have a unique common fixed point.
Proof: Since the pair (A, S) is owc, so there is a point  such that Ax = Sx. Suppose that there exist another point
such that Ax = Sx. Suppose that there exist another point  for which Ay = Sy. We claim that Sx = Sy. By inequality 9) we have,
for which Ay = Sy. We claim that Sx = Sy. By inequality 9) we have,
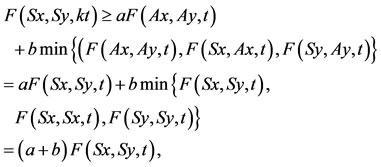
a contradiction, since (a + b) > 1. Therefore Sx = Sy. Therefore Ax = Ay and Ax is unique.
From Lemma 4.1, A and S have a unique fixed point.
5. Acknowledgements
First author is highly thankful to University Grant Commission, New Delhi—11016, INDIA for providing Major Research Project under F. No. 39-41|2010(SR).