Controllability Approach for a Fluid Structure Interaction Problem ()
1. Introduction
Problem involved in fluid structure interactions occur in a wide variety of engineering problem and therefore have attracted the interest of many investigations from different engineering disciplines. As results, much effort has gone into the development of general computational method for fluid structure system by Osses, Fernandez, Quarteroni, Blouza [1-5].
This paper aims at showing a new method to solve fluid structure interaction problem. Our computational method is based on controllability approach. We suppose now that the external force  of the structure depends upon some control parameters belonging to a set K, where K denotes the collection of all admissible controls.
of the structure depends upon some control parameters belonging to a set K, where K denotes the collection of all admissible controls.
We define a payoff functional J. Given a target displacement  does there exist a control
does there exist a control  steering the structural displacement u to
steering the structural displacement u to .
.
We shall now concern ourselves with minimize the functional such that the coupled problem is achievable. To find the optimal control implies the calculus of the displacement u, the velocity of the fluid v and the pressure of the fluid p. The fluid is modeled by two dimensional Stokes equations for steady flow and the structure is represented by the one dimensional beam equation. A former paper has shown both existence and uniqueness solution of the coupled problem Grandmont [6].
2. Presentation of the Problem
We denote by  the two dimensional domain occupied by the fluid,
the two dimensional domain occupied by the fluid, 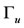 the elastic interface between fluid and structure and
the elastic interface between fluid and structure and  be the remaining external boundaries of the fluid as depicted in Figure 1.
be the remaining external boundaries of the fluid as depicted in Figure 1.  defines the reference domain.
defines the reference domain.
3. Governing Equations
3.1. Structure Equation
We start from the simple equation that governs the structure. The simplified beam equation is:
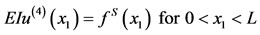 , (1)
, (1)
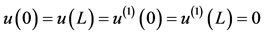 . (2)
. (2)
where u is the displacement of the structure, fS is the external force of the structure, E is the young modulus and I is the moment of inertia. This equation is good representation of the structure for small deformation.
3.2. Fluid Equation
We suppose that the fluid is governing by the Stokes equations for steady flow in :
:
 , (3)
, (3)

Figure 1. Sets appearing to the fluid structure problem.
 (4)
(4)
 , (5)
, (5)
 , (6)
, (6)
where v denotes the fluid velocity, p denotes the pressure, fF denotes the volume force of the fluid, μ the viscosity of the fluid and g denotes the velocity profil of the fluid imposed on the rigid boundary.
4. Fluid Structure Interaction Problem Formulation
The problem is to find u, v and p such that:
 , (8)
, (8)
 , (9)
, (9)
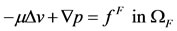 , (10)
, (10)
 , (11)
, (11)
 , (12)
, (12)
 , (13)
, (13)
We have a fluid structure interaction problem. The domain of the fluid depends on the displacement and the displacement depends on the velocity and the pressure of the fluid.
5. Controllability Approach
We call  a control. Corresponding to each control, we consider the coupled problem:
a control. Corresponding to each control, we consider the coupled problem:
 (14)
(14)
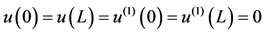 , (15)
, (15)
 , (16)
, (16)
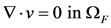 , (17)
, (17)
 , (18)
, (18)
 . (19)
. (19)
and regard u, v and p as the corresponding response of the system. Our overall task will be to determine the beste control for our system. For this we need to specify a specific payoff criterion. Let us define the payoff functional (J):

where u solves the beam equation for the control λ, the target displacement 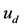 and the real
and the real  are given. Given a target displacement
are given. Given a target displacement  of the structure, we will find a control steering the displacement u to
of the structure, we will find a control steering the displacement u to . Our aim is to find a control
. Our aim is to find a control  which minimizes the payoff (J) subject to Equations (14)-(19).
which minimizes the payoff (J) subject to Equations (14)-(19).
Description of the Method
The weak formulation of the fluid and the structure is given by Grandmont and Murea [6,7]. Thanks to the function BFGS we solve complex nonlinear optimization problem within FreeFem++ Hecht [8]. To solve the problem by the quasi-Newton BFGS method we need the derivative of  with respect to
with respect to .
.
In this work, we use the finite differences method to compute the gradient of . We assume that:
. We assume that:
 .
.
We summarize our controllability approach step by step below:
• Step 1: We solve the Stokes equation by finite elements methods in the reference domain. We find
• Step 2: For a given control and with the pressure  and the velocity
and the velocity  found in step 1, we solve beam equation then we find the displacement
found in step 1, we solve beam equation then we find the displacement
• Step 3: The target displacement 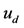 is given. We assume that
is given. We assume that
• Step 4: To minimize J we use the BFGS method. The existence of the optimal control  gives the displacement of the structure u, the velocity of the fluid v and its pressure p. In this step, for each iteration we solve Stokes equation in the moving domain and we compute also the displacement u.
gives the displacement of the structure u, the velocity of the fluid v and its pressure p. In this step, for each iteration we solve Stokes equation in the moving domain and we compute also the displacement u.
6. Numerical Results
We are interested in simulating the blood flow through medium vessel. The wall of the vessel is described by the beam equation and the fluid is the blood which is modeled by the Stokes equations. The parameter values of the fluid and the structure are Mbaye and Murea [9,10]:
Parameter related to fluid: The viscosity of the blood is , its density is
, its density is , the length of the vessel is
, the length of the vessel is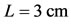 , the half width of the vessel is
, the half width of the vessel is  and the volume force in the fluid is
and the volume force in the fluid is .
.
Parameter related to structure: The thickness of the vessel is h = 0.1 cm, its Young modulus is 
 , and its moment of inertia is
, and its moment of inertia is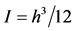 .
.
We assume that the velocity on the boundary fluid domain is  such that
such that 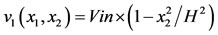 and
and  for all
for all  in
in  . The value of
. The value of  is tested corresponding to the external value of a real pulsatile blood flow,
is tested corresponding to the external value of a real pulsatile blood flow, 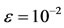 for the computation of the gradient.
for the computation of the gradient.
This given control is  and we take
and we take .
.
We use the P2 Lagrange finite element to approach the velocities and P1 Lagrange finite element is used to approach the pressure. FreeFem++ is used for numerical tests.
7. Results and Discussion
The purpose of this work is to propose a new numerical method to solve fluid structure interaction problems. Our numerical results are presented in Table 1, Figures 2 and 3. Figure 2 displays the behavior of the fluid flow through the vessel and the displacement of the structure after 5 iterations. Figure 3 displays the pressure wave of the fluid after 5 iterations. Comparing our results to Mbaye and Murea [9,10], we realize that the pressure

Table 1. Payoff functional and control for 5 iterations.

Figure 2. Fluid velocity and structure displacement.
wave, the fluid flow and the displacement of the structure are on good behavior. On the one hand, the advantage of the method compared to Mbaye and Murea [9,10] is that we don’t need to approximate the pressure on the interface by a linear combination of functions and compute the analytic solution of the structure equation. The fact that we don’t need to increase the number of controls in order to obtain good results Murea [10], is another advantage of this method on the other hand. To improve our paper, we will introduce in a future work an analytic derivative of the cost function with respect to control.
8. Conclusion
In this work, a new numerical method based on the controllability approach is used to solve fluid structure interaction problem. Our method gives good results when the displacement is small. After five iterations we reach the solution of the coupled problem. In a forthcoming work, the technique used here will be adapted to solve the unsteady fluid structure interaction problem.
9. Acknowledgements
The author wish to thank Professor Djaraf Seck for fruitful discussion on this subject.