Introduction to the Theory of Relativity of Non-Inertial Systems and Mechanics of the Universe ()
1. Introduction
The Special Theory of Relativity (STR) is a fundamental physical theory, which has an extremely narrow limit of applicability. It is limited by the inertial reference systems (IRS). In nature rigorous IRS does not exist. The real reference systems are always associated with massive bodies (reference bodies), but massive bodies themselves affect to the process flow.
To eliminate this constrain A. Einstein replaced the special principle of relativity with the general one, considering above the general principle of relativity (GPR) the equivalence of all systems. V. A. Fock has opinion, that it is physically unacceptable. He says, that GPR denies availability privileged systems, this leads to equivalence of geocentric and heliocentric systems, that is absurd and contrary to observations [1].
Main objections based on fact, that Einstein did not offer concrete group of coordinate transformation, similar to Lorenz’s transformations, which conserves general covariance of nature laws and allows differ one RS (Sun for example) from another (Earth for example), select preferred system, take into account their influence on the processes occurring in them. Instead this A. Einstein offered the system of geometrized equations-General Theory of Relativity (GTR), in which relativity was not complete. The reason is that in real systems, systems connected to the massive bodies (MRS), the forces of inertia characterize property of the space but not of the body. Choice of an accelerated reference system implies the existence of absolute space, because there is no other object, on which accelerated motion would generate the force of inertia.
Nature of inertia is not investigated at this time and appreciates with no one of four fundamental forces. Only hypothesis, which in some degree relates inertia and matter is Mach principle (MP) [2]. In order to explain MP we give concrete example.
Assume that we have two massive bodies as preset, Earth and Sun for example, which is associated with the MRS . Lets
. Lets  rests and
rests and  rotates relative to S with a constant angular velocity
rotates relative to S with a constant angular velocity  in the plane
in the plane . Coordinates in these systems are related by equations Figure 1.
. Coordinates in these systems are related by equations Figure 1.
 (1.1)
(1.1)

Figure 1. Reference system S' is rotating relative to reference system S with angular velocity ω.
Define the same coordinates relative to the system S'
 (1.2)
(1.2)
The systems are as they reversed. Now S rotates relative to S'. This we can observe daily, observing sunrise, sunset and Moon. It seems that Earth is at rest and sky is circling. It’s indifferent to observer, which body is considered at rest and which body is moving. In both cases he watches the same pictures. However, precise experiments such as the experiments with the Foucault pendulum show that the situations are distinguishable. In the stationary system, the inertial forces do not appear, but in the rotating system this forces appear independently from the stationary.
MP answers the question about the nature of this forces and why they appear only in one of two kinematicaly equal systems S and S'. In this principle system S is not resting alone, it is resting together with the all other bodies of the Universe. This bodies formed one-piece global reference system  and this system S rotates relative to this global system. Consequently, the inertia force would appear in the stationary system S, if
and this system S rotates relative to this global system. Consequently, the inertia force would appear in the stationary system S, if  rotates around S. But MP does not explain the mechanism of inertia appearance and does not allow calculating the intensity.
rotates around S. But MP does not explain the mechanism of inertia appearance and does not allow calculating the intensity.
2. Hypothesis about the Induction Nature of Inertia
Given that the inertial forces occur only when the speed changes, we have offered hypothesis about the induction nature of inertia. According to this hypothesis, every particle, which produces a static field Sn at rest, produces a dynamic field Dn in motion. Union of dynamic fields creates the united field of matter, which we call the inertial field (IF). Name comes from the fact, that the interaction of a moving body with the field forms a special momentum  and change of
and change of  induces inertia forces. Regarding to the MP, it means that bodies, moving relative to each other, generate IF that fills the entire space, creating some of the quasi-elastic environment that prevents acceleration. The reaction of this environment against forces seeking to change the state of a body is the response of the Universe, which is perceived as inertia of the body.
induces inertia forces. Regarding to the MP, it means that bodies, moving relative to each other, generate IF that fills the entire space, creating some of the quasi-elastic environment that prevents acceleration. The reaction of this environment against forces seeking to change the state of a body is the response of the Universe, which is perceived as inertia of the body.
Introduction of this momentum converts space into force field, which acts on processes, which going in this field. Second Newton’s law in non-inertial reference systems (NIRS) takes the same view as in IRS.
 ,
,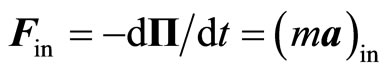 (2.1)
(2.1)
Forces of inertia are located аnd the mechanical momentum 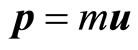 assumes new field component
assumes new field component , defining interaction between moving body and other bodies of the Universe. Interaction has field character. In first approximations we represent it as sum of products of all kinds of charges
, defining interaction between moving body and other bodies of the Universe. Interaction has field character. In first approximations we represent it as sum of products of all kinds of charges 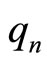 (electric, gravitational, color etc.) of moving body and 4-vector potential
(electric, gravitational, color etc.) of moving body and 4-vector potential , instantiated by other bodies.
, instantiated by other bodies.
 (2.2)
(2.2)
where U-potential energy, c-velocity of distribution IF in specified medium. Full momentum of the body contained from sum of mechanical and field momentum
 (2.3)
(2.3)
The hypothesis is based on two fundamental laws of nature: the law of inverse squares, leading to the Poisson equation
 (2.4)
(2.4)
and law of charge conservation
 (2.5)
(2.5)
where  and
and  are density and flux of charges and
are density and flux of charges and ,
, 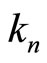 are corresponding coupling constants. Jointly solving these equations, we have
are corresponding coupling constants. Jointly solving these equations, we have
 (2.6)
(2.6)
Argument of the divergence is a constant or rotor of the dynamic field . First variant is physically unacceptable, and from second we get
. First variant is physically unacceptable, and from second we get
 (2.7)
(2.7)
In such a way, any kind of charges , which produces static field
, which produces static field , produces dynamic field
, produces dynamic field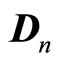 . Dynamic field of electrical charge is known as magnetic field. Dynamic fields of other charges is unknown, but they existence is predicted by the two fundamental laws.
. Dynamic field of electrical charge is known as magnetic field. Dynamic fields of other charges is unknown, but they existence is predicted by the two fundamental laws.
3. Transformation of Coordinates in Non-Inertial Systems
It follows from (2.1), if external forces do not act on the moving body, its 4-momentum (2.3) is preserved, and the body will continue its motion with constant 4-velocity
 (3.1)
(3.1)
If we bind MRS with such a body, it will be inertial. We cannot apply the postulates of relativity to this MRS, because, firstly, it is uncertainty relative to what body this system is moving, and secondly, it is unclear how to reconcile data of different MRS. We can not compare the data from different reference systems, if those measuring devices are not concordant. If we proceed from MP, then answer to first question is obvious to all bodies of the universe. How to determine their speed, with no center, no isolated point, which could be taken as the origin? The introduction of the  -momentum removes this question. As reference point can be taken any point of space, because the influence of the surrounding matter at this point is taken into account in IF, and can be measured.
-momentum removes this question. As reference point can be taken any point of space, because the influence of the surrounding matter at this point is taken into account in IF, and can be measured.
Measuring instrument’s identifications can also be achieved if their scales calibrates as a functions of all quantities which affect on the testimonies. Then the scales become variables and change automatically when moving from one MRS to another and the ratio of the measured values remains the same in all MRS, regardless of the mass of bodies with which they are associated.
Such representation of MRS is called Mach-Poincare’s relativity principle (MPRP). It says, if the physical process are changing simultaneously and proportionally to the testimony of all measuring instruments, then no experiments is possible to detect this change. To establish a mutual correspondence, systems should exchange information. Information carrier can be any signal (light, sound, smell etc.), which is distributed freely in this environment. In empty space, a carrier can only be a light wave. The speed of light is constant, and in the environment can be changed arbitrarily, but the ratio  is conserved in all MRS.
is conserved in all MRS.
We take the light as a measuring standard and as the fourth coordinate  and where
and where  and
and  are the time lengths of one and the same process in free space and in the potential field U. From the conservation of 4-momentum
are the time lengths of one and the same process in free space and in the potential field U. From the conservation of 4-momentum , for
, for  we have
we have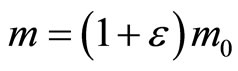 . Another relation gives the MPRP, which requires that 4-volume
. Another relation gives the MPRP, which requires that 4-volume  conserve in all systems.
conserve in all systems.
From these definitions the following changes to the clock testimony, scales and rulers at different points of space are
 (3.2)
(3.2)
Factor  is the scale factor, which determines the effect of a static potential field (curvature) on the measurement instruments testimony. In representation of MPRP empty space is flat and influence of matter, causing him bending is taken into account, linkage between the coordinates of points
is the scale factor, which determines the effect of a static potential field (curvature) on the measurement instruments testimony. In representation of MPRP empty space is flat and influence of matter, causing him bending is taken into account, linkage between the coordinates of points  and
and  can be represented as Figure 2.
can be represented as Figure 2.
 (3.3)
(3.3)
 (3.4)
(3.4)
Lets system  rests and
rests and  moving relative to it with unrestricted velocity
moving relative to it with unrestricted velocity . Metric coefficients
. Metric coefficients  are proportional to velocity, but velocity is relative, therefore should be
are proportional to velocity, but velocity is relative, therefore should be
 (3.5)
(3.5)

Figure 2. Reference system S' is moving relative to reference system S.
Coefficients  have define so general covariance of physical law was enforced for any choice of MRS, type of signal and its velocity. This requires that the Jacobian of coordinate transformation is equal to one.
have define so general covariance of physical law was enforced for any choice of MRS, type of signal and its velocity. This requires that the Jacobian of coordinate transformation is equal to one.
 (3.6)
(3.6)
These conditions are sufficient to establish a connection between the coordinates  and
and . Introducing the notation
. Introducing the notation
 (3.7)
(3.7)
and jointly solving (3.4)-(3.7), we obtain
 (3.8)
(3.8)
or separating the variables
 (3.9)
(3.9)
 (3.10)
(3.10)
where  and
and  are parameters of separations. We represent it in exponential form
are parameters of separations. We represent it in exponential form
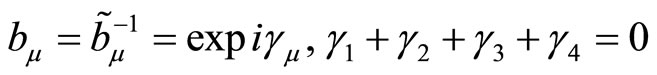 (3.11)
(3.11)
Substituting these values in (3.3), we obtain generalized group of coordinate transformations MRS 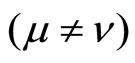
 (3.12)
(3.12)
The group contains two types of unknown variables.
Unknowns 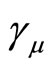 make sense phase angle and are arbitrary, and
make sense phase angle and are arbitrary, and  characterize metric of the system and are
characterize metric of the system and are
 (3.13)
(3.13)
Following from (3.13), the coordinates of events in the MRS is uniquely determined by the relative change of energy-momentum of signal, which connects S and S’. If this change is small, group (3.12) becomes the Galilean transformation. If this change due only to the participation of the signal in relative motion mass-less IRS group becomes the Lorentz transformation. In all other cases MRS is distinguishable and has different effects on the course of the process. But this distinction does not violate the general covariance of laws of nature with respect to arbitrary MRS.
4. Energy and Momentum of Particle (Body) in Inertial Field
In determining the velocity and momentum, we proceeded from the quasi-classical approximation of these quantities, which is not quite correct, because the quasiclassical approximation allows long-range action. The definition should be based on the group (3.12). Using this group, we form the momentum
 (4.1)
(4.1)
 (4.2)
(4.2)
We define force, differentiating momentum with respect to time
 (4.3)
(4.3)
where
 (4.4)
(4.4)
The fourth component of the momentum determines the energy . Taking into account that the vectors are orthogonal, we find
. Taking into account that the vectors are orthogonal, we find
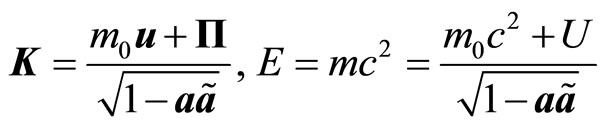 (4.5)
(4.5)
 (4.6)
(4.6)
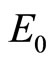 is energy of a particle, resting in a potential field
is energy of a particle, resting in a potential field . These formulas differ from the corresponding formulas of SRT by presence of
. These formulas differ from the corresponding formulas of SRT by presence of  potentials and that they are valid for any system. They, in particular, show that the inertial mass depends not only on velocity. But it is a function of the energy of interaction at all. Particle in a state with potential energy
potentials and that they are valid for any system. They, in particular, show that the inertial mass depends not only on velocity. But it is a function of the energy of interaction at all. Particle in a state with potential energy  has a mass
has a mass 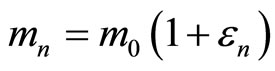 and in the transition to a state with potential energy
and in the transition to a state with potential energy  its mass changes in quantity
its mass changes in quantity
 (4.7)
(4.7)
Change is due to the fact that every medium has a maximum flow capacity, characterized by some critical velocity , which can not be exceeded under these conditions. If the particle is energize with E excess threshold of kinetic energy Ek, then excess energy
, which can not be exceeded under these conditions. If the particle is energize with E excess threshold of kinetic energy Ek, then excess energy  arise and it can not be used to increase speed. This excess energy is either radiated or converted to other forms of energy, either uses to from a new particle. For electromagnetic interactions
arise and it can not be used to increase speed. This excess energy is either radiated or converted to other forms of energy, either uses to from a new particle. For electromagnetic interactions , where
, where  is the fine structure constant. For nuclear interaction this ratio is an order of magnitude, but not enough to form a new particle. New particles are produced by the collision of high energy particles, then one of particles receive huge energy for a short time, which cannot be quickly radiated. Therefore it is impossible to observe the same particles in different energy states as different particles.
is the fine structure constant. For nuclear interaction this ratio is an order of magnitude, but not enough to form a new particle. New particles are produced by the collision of high energy particles, then one of particles receive huge energy for a short time, which cannot be quickly radiated. Therefore it is impossible to observe the same particles in different energy states as different particles.
5. Equations of Motion in Inertial Field
We set up equation of motion of the body in the IF. For simplicity, we assume that the medium have no matter except IF. In this case, the Lagrangian can be formed only from the complete 4-momentum. We choose it as
 (5.1)
(5.1)
Performing standard calculations, we obtain [3]
 (5.2)
(5.2)
where
 (5.3)
(5.3)
 (5.4)
(5.4)
Measurements is performed in the local time 
 . Two forces act on the body in IF-radial (Q), and axial (
. Two forces act on the body in IF-radial (Q), and axial ( ). Radial force is sum of two dissimilar components-force of inertia and potential force. Axial force depends on velocity of the body V, and circular vector field R. This force appears first time in mechanics and plays important role in shaping the structure of the Universe.
). Radial force is sum of two dissimilar components-force of inertia and potential force. Axial force depends on velocity of the body V, and circular vector field R. This force appears first time in mechanics and plays important role in shaping the structure of the Universe.
The system of differential equations of the inertial field follows from (2.4) and (5.3).
 (5.5)
(5.5)
Fields, composing this system, related to the fields of single particles with material equations
 (5.6)
(5.6)
 and
and 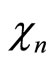 are coupling constants, their ratio determines the maximal possible velocity of distribution of individual fields.
are coupling constants, their ratio determines the maximal possible velocity of distribution of individual fields.
 (5.7)
(5.7)
All this fields composed from common field 4-momentum 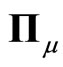 and its derivatives
and its derivatives
 (5.8)
(5.8)
These equations is completely solving the problem of inertia and founding out its physical nature and sources. Thus, a new relativistic mechanics is created. This mechanics eliminates the shortcomings of Newtonian mechanics and STR. The law of inertia applies to all types of motion, the need to postulate IRS disappears.
We show that these equations are invariant under the group (3.12). Introducing tensor of IF strength
 (5.9)
(5.9)
with components

rewrite Equations (5.2)-(5.5) in four-dimension form
 (5.10)
(5.10)
Taking into account the variations of tensor
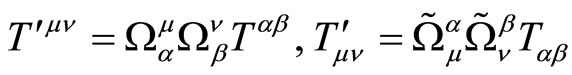 (5.11)
(5.11)
It’s easy to verify that Equation (5.10) is invariant relative to the group (3.12) and field components are transformed as


 (5.12)
(5.12)
For Galilean systems, they become the corresponding formulas of STR.
6. Unified System of Electrodynamics and Gravidynamics Equations
Consider the motion of electrically charged particles in the IF. A particle is a carrier of two kinds of chargeelectric  and gravitational (mass)
and gravitational (mass) . Assuming
. Assuming 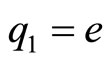 ,
,  , and
, and , we have
, we have
 (6.1)
(6.1)
where ,
,  are values of electric and gravitational vectors,
are values of electric and gravitational vectors,  ,
, 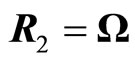 are vectors of magnetic and gravy-magnetic (inertial) inductions. Substituting in (5.5), we obtain a unified system of electric and gravidynamics equations.
are vectors of magnetic and gravy-magnetic (inertial) inductions. Substituting in (5.5), we obtain a unified system of electric and gravidynamics equations.
 (6.2)
(6.2)
where 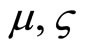 is magnetic and inertial (gravy-magnetic) permeability;
is magnetic and inertial (gravy-magnetic) permeability;  are densities of electric and gravitational charges. Relations of these fields determine the trajectory of a particle. In micro-world influence of gravyinertial field (GIF) is neglected. Then we obtain the system of equations of electrodynamics. In mega-world contrary influence of these fields dominates and influence of electromagnetic fields is neglected. When we obtain similar gravidynamics equations set. It shows that gravitational and inertial fields are interrelated, induce each other and form unified GIF. That field carries flow of energy, momentum and distributes with velocity
are densities of electric and gravitational charges. Relations of these fields determine the trajectory of a particle. In micro-world influence of gravyinertial field (GIF) is neglected. Then we obtain the system of equations of electrodynamics. In mega-world contrary influence of these fields dominates and influence of electromagnetic fields is neglected. When we obtain similar gravidynamics equations set. It shows that gravitational and inertial fields are interrelated, induce each other and form unified GIF. That field carries flow of energy, momentum and distributes with velocity
 (6.3)
(6.3)
This value is unknown, but row of indirect evidences, that in vacuum it coincides with the speed of light, exist. Taking this model into account, we determine constant of vacuum of the inertial field
 (6.4)
(6.4)
This is an extremely small quantity. Its smallness may explain why IF conventional bodies are not observed. It is large only in the scale of the Universe, and plays an important role in shaping her structure.
7. Unified Effects of STR and GTR New Effect
Effects of SRT are not seen, because performing standard calculations, we obtain the same formulas of SRT. The difference is that we obtain a more general expression of  instead of ratio of light’s and body’s velocities.
instead of ratio of light’s and body’s velocities.
The gravitational shift of the spectrum, the deviation of ray of light in a gravitational field and rotation of planet’s perihelion-these three effects usually interpret as deviation from Newton’s laws and triumph of GTR. The first effect expresses the law of energy conservation and follows from Newton’s laws. It has been confirmed by experiments of Pound and Rebka. The second effect also follows from Newton’s laws, and has been calculated by Soldner. He showed that ray of light, passing at massive body m at distance l, deviates by an angle
 (7.1)
(7.1)
For Sun it is 0.87 arc seconds. GTR gives a value twice a much-1.7. This angle has been measured many times, but because of its smallness measurement results can not be interpreted unambiguously in favor of one or another theory, but rounding is in favor of GTR. There we want to draw attention to another effect the axial displacement of the ray of light. It was observed first time by Eddington in 1919 during a solar eclipse in South America. Three years later this effect was observed by Campbell and Tryumpler, and than in 1973 by Jones etc. But because it is unpredicted by theory, it was ignored [3].
We show that axial ray deviation is such reality as radial deviation. According to this theory, the Newtonian  and inertial
and inertial  forces act on ray of light. Light passing at a massive body with velocity
forces act on ray of light. Light passing at a massive body with velocity  is affected by IF
is affected by IF
 (7.2)
(7.2)
and deflected by an angle
 (7.3)
(7.3)
If we replace value of  by its value from (6.4), then the angles
by its value from (6.4), then the angles 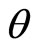 and
and  will match. But they can not be summed, because they lie in orthogonal planes. Thus, a ray of light passing at a massive body, is deviated not only in the direction of the body, but tends to revolve around power lines of its IF, like an electron in a magnetic field. If the IF is weak, the ray, describing the helix with a big step, leaving the field. This is a new effect, and it requires independent confirmation.
will match. But they can not be summed, because they lie in orthogonal planes. Thus, a ray of light passing at a massive body, is deviated not only in the direction of the body, but tends to revolve around power lines of its IF, like an electron in a magnetic field. If the IF is weak, the ray, describing the helix with a big step, leaving the field. This is a new effect, and it requires independent confirmation.
The third effect is most interesting, because it is absent in Newton’s laws. If the body of mass 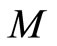 rotates in an elliptical orbit, then it creates IF in the center.
rotates in an elliptical orbit, then it creates IF in the center.
 (7.4)
(7.4)
where  is average radius of the orbit,
is average radius of the orbit,  is major axis,
is major axis,  is eccentricity,
is eccentricity,  is orbital period. In this case the body is a planet and in the solar IF it obtains an inertial angular momentum
is orbital period. In this case the body is a planet and in the solar IF it obtains an inertial angular momentum  in addition to the mechanical angular momentum
in addition to the mechanical angular momentum . It is half of mechanical and have the same direction as the mechanical angular momentum. Planet with a common angular momentum
. It is half of mechanical and have the same direction as the mechanical angular momentum. Planet with a common angular momentum  will precess with frequency
will precess with frequency  in this field and for the time
in this field and for the time  will be shifted in direction of motion by the angle
will be shifted in direction of motion by the angle
 (7.5)
(7.5)
If the observation period is one hundred Earth years ( ), then for Mercury (T = 87.97 days, b = 5.8 × 1010 m, e = 0.2956, M = 1.983 × 1030 kg), we obtain
), then for Mercury (T = 87.97 days, b = 5.8 × 1010 m, e = 0.2956, M = 1.983 × 1030 kg), we obtain  arc seconds. This is in excellent agreement with observations.
arc seconds. This is in excellent agreement with observations.
8. Flat Rotation of Celestial Bodies and the Problem of Dark Matter
The main feature of the celestial bodies is that they are rotating and in addition in the same plane. The reasons for this feature is not discussed, it is assumed that the body got an angular momentum as a result of random collisions. The rotation is so widespread and regular phenomenon that can not be explained by random factors. The rotation should have a permanent source. Such a source may be an inertial field. Every body in this field acquires inertial angular momentum and will begin the rotation.
Suppose that some object, such as the Galaxy, created a powerful IF and its center was a very massive body M, like the Sun. Let other, less massive body with mass m, moving with speed V, falls into this field. Gravy-inertial force will act on it (5.2). We choose coordinate system so that the axis z coincides with the direction of IF .
.  Expanding the force into a components, and considering that
Expanding the force into a components, and considering that
 (8.1)
(8.1)
we obtain
 (8.2)
(8.2)
let the body moves along axis z, then , assuming
, assuming ,
,  , we combine the first two equations
, we combine the first two equations
 (8.3)
(8.3)
Away from the gravitational field  the equation admits a particular solution
the equation admits a particular solution . It shows that the IF carries the body along and causes its rotation with angular velocity
. It shows that the IF carries the body along and causes its rotation with angular velocity .
.
Still in the thirties of last century astronomers discovered one of displays of dark matter. The orbital velocities of some galaxies are so enormous that the mass of clusters, they are rotating around, is not sufficient to keep them.
But because the galaxies do not leave their orbit, hypothesis of the dark mass  existence had been offered to allow use of Kepler’s law
existence had been offered to allow use of Kepler’s law
 (8.4)
(8.4)
Sensational message was made in 1998. This message is about that the orbital velocity of the galaxies does not depend on their position relative to the center of clusters, it is the same near and far from the center. For the explanation of it hypothesis of invisible parties existence had been offered (neutralinos, axons, space vacuum etc.) [4].
Suppose that the galaxy is rotating in the IF in a circular orbit of radius r. Then  is superimposed by the Keplerian orbital rotation.
is superimposed by the Keplerian orbital rotation.
 (8.5)
(8.5)
Body’s rotation creates in center an IF equals to
 (8.6)
(8.6)
where T is orbital period. Linear velocity of a body at distance r is equal
 (8.7)
(8.7)
At large distances the second term vanishes, and the speed becomes constant and equal to .Thus, the anomalies in the rotation of galaxies are not caused by the presence of dark matter, but they are caused by the imperfection of Newton’s laws.
.Thus, the anomalies in the rotation of galaxies are not caused by the presence of dark matter, but they are caused by the imperfection of Newton’s laws.
We draw attention to another important effect. We assume that the trajectory of the body passes at massive body at close range. Then the body is captured by field, it will oscillate with amplitude h and frequency
 (8.8)
(8.8)
Oscillations  and
and  occurs in different planes, so the trajectory is not a continuous line, but is a spiral, closed in a ring. Body nods while moving. If GIF intersects not single body, but and a swarm of small particles, they form concentric rings, like Saturn’s rings. In the photos of Jupiter and Saturn, it is easy to find the parallel dark stripes. This is stream of drifting particles, which eventually settle to the equatorial plane of the planet and form the next ring.
occurs in different planes, so the trajectory is not a continuous line, but is a spiral, closed in a ring. Body nods while moving. If GIF intersects not single body, but and a swarm of small particles, they form concentric rings, like Saturn’s rings. In the photos of Jupiter and Saturn, it is easy to find the parallel dark stripes. This is stream of drifting particles, which eventually settle to the equatorial plane of the planet and form the next ring.
All planets are rotating in the equatorial plane of the Sun, the planets rings are concentric, the galaxies have a flat disklike shape and the spiral arms. These facts leave no doubt that they are formed by the IF. It is the true architector of the Universe.
9. United Doppler and Einstein’s Effect
The main source of information about the Universe is a shift of spectral lines. The shift is caused by many reasons. Suppose a distant star S sends a signal to Earth  in the form of monochromatic wave with frequency
in the form of monochromatic wave with frequency . Terrestrial observer, receiving the signal compares its frequency to the frequency of the owner signal
. Terrestrial observer, receiving the signal compares its frequency to the frequency of the owner signal , and finds out that it differs on
, and finds out that it differs on . This difference is caused by two reasons: participation in a relative motion of earth-star, and the interaction with the particles of the medium. Using group (3.12), we establish the relationship between these frequencies
. This difference is caused by two reasons: participation in a relative motion of earth-star, and the interaction with the particles of the medium. Using group (3.12), we establish the relationship between these frequencies
 (9.1)
(9.1)
 (9.2)
(9.2)
where e is elementary vector in the direction of light propagation. Left side defines the longitudinal and transverse Doppler’s effect, right side defines Einstein’s effect, the gravitational shift of the spectrum. Pay attention to the fact that we did not suppose that the star is moving. But the effect of IF on the light is momentum, like the star is moving. That characterizes the relativity of every movement.
The number of examples can be increased hundredfold.
10. Conclusion
Thus existence of new force with induction nature is totally proved. Use of calculation described above allows to make simpler and more precise picture of Universe’s structure.
11. Acknowledgements
We are grateful to participants of the theoretical seminars in IGPAS and MSU headed by Prof. A. A. Rukhadze and Prof. V. Yu. Vladimirov for discussions and criticism.