1. Introduction
Ranking portfolio return distributions is one of the key procedures which can be used by quantitative analysts to provide support to the decisional processes of portfolio managers. In this paper we discuss ranking criteria for skew-normal distributions based on stochastic dominance rules of first and second order; we refer the reader to Levy ([1]) for a detailed exposition of these concepts and many related results.
The economical motivation underpinning second order stochastic dominance (SSD) is particularly appealing: a representative investor with increasing and concave utility function will always prefer a portfolio 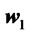 to a portfolio
to a portfolio 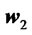 if the the returns of
if the the returns of 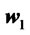 stochastically dominate at the second order the returns of
stochastically dominate at the second order the returns of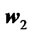 . SSD encapsulates therefore the concept of risk-aversion. Investments theorists and practitioners have developed along the times several methods to compare risky investments prospects or portfolios of assets and choose among the feasible ones in some optimal way: the review paper Brandt ([2]) and the book Sharpe et al. ([3]) discuss many of these methodologies. Probably the Markowitz’s mean-variance framework, Markowitz ([4]), remains the most famous approach, even if it is has well documented intrinsic limitations. There have been various attempts to overcome some of these limitations: by taking into account higher distributional moments as in Athayde et al. ([5]), by investigating bayesian versions of the Markowitz’s idea as in Pastor ([6]) and Polson ([7]), or by proposing alternative or more general risk measures as in Konno and Yamazaki ([8]), Markowitz et al. ([9]) and Feiri et al. ([10]). A very original and influential contribution to the asset allocation problem has been given by Black and Litterman in Black and Litterman ([11]): there the authors nicely incorporate in their framework subjective beliefs or “views” on expected future returns of assets (see Meucci ([12]) for a survey and extensions). Skewnormally distributed returns, which we handle in this paper, have been already considered in portfolio theory by Adcock and Shutes ([13]) and Harvey et al. ([14]), furthermore Adcock ([15]) and Bacmann and Massi-Benedetti ([16]) contain interesting applications to hedge funds portfolios. However, to our best knowledge, the stochastic dominance approach for comparing skewnormally distributed returns is considered here for the first time. Notice that stochastic dominance rules aim to compare the whole distribution and not just a limited number of its moments. Finally we refer to Post ([17]) for applications of stochastic dominance rules to empirical data. This paper is organized as follows. In the next section we consider markets with skew-normal returns and portfolios on these markets; in Section 3 we show that even in markets with normal returns in the basic securities there can be portfolios exhibiting skewnormality in their returns if on the same market derivatives based strategies with V-shaped payouts can be implemented. In Section 4 we prove our stochastic dominance criteria and illustrate some possible applications.
. SSD encapsulates therefore the concept of risk-aversion. Investments theorists and practitioners have developed along the times several methods to compare risky investments prospects or portfolios of assets and choose among the feasible ones in some optimal way: the review paper Brandt ([2]) and the book Sharpe et al. ([3]) discuss many of these methodologies. Probably the Markowitz’s mean-variance framework, Markowitz ([4]), remains the most famous approach, even if it is has well documented intrinsic limitations. There have been various attempts to overcome some of these limitations: by taking into account higher distributional moments as in Athayde et al. ([5]), by investigating bayesian versions of the Markowitz’s idea as in Pastor ([6]) and Polson ([7]), or by proposing alternative or more general risk measures as in Konno and Yamazaki ([8]), Markowitz et al. ([9]) and Feiri et al. ([10]). A very original and influential contribution to the asset allocation problem has been given by Black and Litterman in Black and Litterman ([11]): there the authors nicely incorporate in their framework subjective beliefs or “views” on expected future returns of assets (see Meucci ([12]) for a survey and extensions). Skewnormally distributed returns, which we handle in this paper, have been already considered in portfolio theory by Adcock and Shutes ([13]) and Harvey et al. ([14]), furthermore Adcock ([15]) and Bacmann and Massi-Benedetti ([16]) contain interesting applications to hedge funds portfolios. However, to our best knowledge, the stochastic dominance approach for comparing skewnormally distributed returns is considered here for the first time. Notice that stochastic dominance rules aim to compare the whole distribution and not just a limited number of its moments. Finally we refer to Post ([17]) for applications of stochastic dominance rules to empirical data. This paper is organized as follows. In the next section we consider markets with skew-normal returns and portfolios on these markets; in Section 3 we show that even in markets with normal returns in the basic securities there can be portfolios exhibiting skewnormality in their returns if on the same market derivatives based strategies with V-shaped payouts can be implemented. In Section 4 we prove our stochastic dominance criteria and illustrate some possible applications.
2. Portfolios in Skew-Normal Markets
Following Azzalini ([18]) let us recall that a random vector 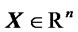 is said to follow the skew-normal distribution with location parameter
is said to follow the skew-normal distribution with location parameter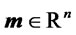 ,
, 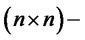 scale matrix
scale matrix 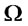 and shape parameter
and shape parameter 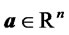 if its density has the form:
if its density has the form:
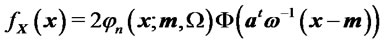 (1)
(1)
where  is the diagonal matrix
is the diagonal matrix
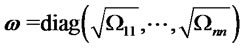 ,
, 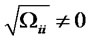 for
for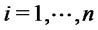 ,
,
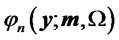 is the density of a
is the density of a 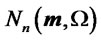 -random vector and
-random vector and 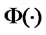 is the cumulative distribution function of a univariate standard normal. In this case we write
is the cumulative distribution function of a univariate standard normal. In this case we write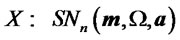 . In particular, in the univariate case,
. In particular, in the univariate case,  has the skew-normal distribution of parameters
has the skew-normal distribution of parameters 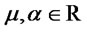 and
and 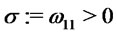 if for all
if for all 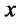
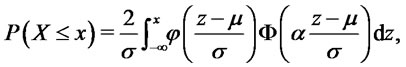
where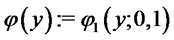 . In this case we write
. In this case we write
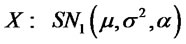 . Clearly for
. Clearly for 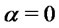 we have
we have
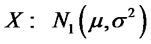 . For
. For 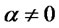 the distribution is skewed and indeed its mean, variance and skewness can be easily computed. They are respectively given by:
the distribution is skewed and indeed its mean, variance and skewness can be easily computed. They are respectively given by:

with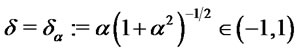 .
.
We refer the reader to Arellano and Azzalini ([19]) and Genton ([20]) for further properties and many interesting applications.
Let us now consider a market with 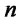 basic risky assets whose future returns, at time
basic risky assets whose future returns, at time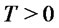 , are described by a random vector
, are described by a random vector 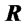 such that:
such that:
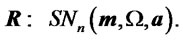 (2)
(2)
An investor, the decision maker, is facing with the problem of allocating her initial capital on the market by choosing a portfolio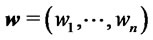 , with
, with 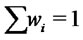 and holding it unchanged up to time
and holding it unchanged up to time . The portfolio return is given by the random variable
. The portfolio return is given by the random variable 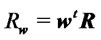 with:
with:
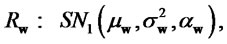 (3)
(3)
and parameters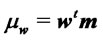 ,
, 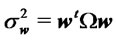 , and
, and
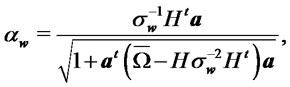 (4)
(4)
where 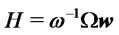 and
and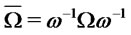 , see Azzalini ([18]). Henceforth it is clear that in order to compare the returns of two different portfolios
, see Azzalini ([18]). Henceforth it is clear that in order to compare the returns of two different portfolios 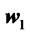 and
and 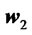 on this market we must have at our disposal criteria which allow us to compare two univariate skew-normal random variables. In Section 4 we prove simple criteria based on stochastic dominance, Levy ([1]). Although we only make use of standard techniques, to our best knowledge these results have never been discussed in the classical literature on the subject. An investor can use them to discard a portfolio or a family of portfolios whose returns are stochastically dominated by the return of another portfolio.
on this market we must have at our disposal criteria which allow us to compare two univariate skew-normal random variables. In Section 4 we prove simple criteria based on stochastic dominance, Levy ([1]). Although we only make use of standard techniques, to our best knowledge these results have never been discussed in the classical literature on the subject. An investor can use them to discard a portfolio or a family of portfolios whose returns are stochastically dominated by the return of another portfolio.
3. Portfolios Including Derivative Securities in Normal Markets
In this section we briefly show how the skew-normal return distributions can naturally appear even in markets with normal returns in the primary risky assets, if in the same markets are traded derivative securities which incorporate non-linear pay-offs. More specifically consider markets for which the shape parameters of the basic risky assets are all zero (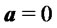 ), that is
), that is
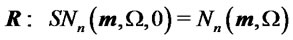 (5)
(5)
and suppose that a straddle on one of the assets is available at a cost 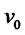 and strike price
and strike price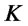 . To simplify the exposition we fix
. To simplify the exposition we fix 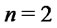 and denote by
and denote by 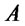 and
and 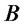 the market basic risky securities; therefore their returns over the interval
the market basic risky securities; therefore their returns over the interval 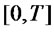 will follow the law:
will follow the law:
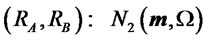 (6)
(6)
with 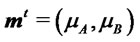 and
and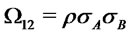 . Let
. Let 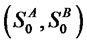 be their present spot prices, a straddle is written on the first asset and will pay to the holder
be their present spot prices, a straddle is written on the first asset and will pay to the holder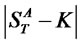 ,
, 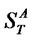 denoting the asset price at maturity date
denoting the asset price at maturity date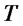 . Consider an investor who wishes to allocate percentages of her capital both on the straddle and on shares of asset
. Consider an investor who wishes to allocate percentages of her capital both on the straddle and on shares of asset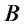 , while investing the remaining part on a risk-free bond. It turns out that for a strike value
, while investing the remaining part on a risk-free bond. It turns out that for a strike value 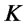 equal to
equal to 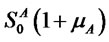 the portfolios returns will display skew-normality. This condition on
the portfolios returns will display skew-normality. This condition on 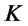 appears to be very stringent, however in practice we could have
appears to be very stringent, however in practice we could have 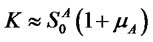 with returns distribution close to skew-normality. Notice that the case
with returns distribution close to skew-normality. Notice that the case  corresponds to a straddle traded “at the money” (this particular case, and with
corresponds to a straddle traded “at the money” (this particular case, and with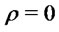 , has been discussed by Blasi ([21])). Indeed denoting by
, has been discussed by Blasi ([21])). Indeed denoting by 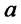 the percentage of initial capital invested on the straddle on asset
the percentage of initial capital invested on the straddle on asset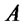 , by
, by 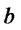 the percentage of initial capital invested on asset
the percentage of initial capital invested on asset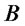 , the return of the portfolio
, the return of the portfolio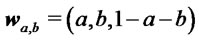 , at time
, at time 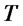 will be
will be
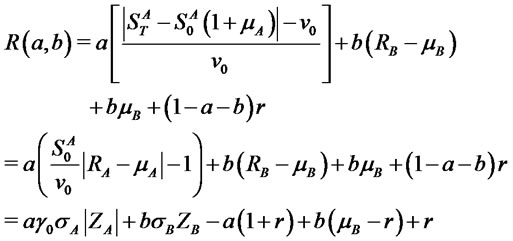 (7)
(7)
where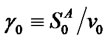 ,
, 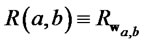 ,
, 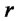 is the bond yield and standardized assets returns have been denoted by
is the bond yield and standardized assets returns have been denoted by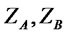 . We notice that a decomposition analogous to (7) continues to hold also for the multi-asset case (
. We notice that a decomposition analogous to (7) continues to hold also for the multi-asset case (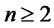 ), that is for portfolios investing on a straddle on one of the assets, on shares of the remaining
), that is for portfolios investing on a straddle on one of the assets, on shares of the remaining 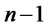 risky assets and on the risky-free asset. The following result is a straightforward generalization of a result by Henze ([22]) and can be proven by elementary methods:
risky assets and on the risky-free asset. The following result is a straightforward generalization of a result by Henze ([22]) and can be proven by elementary methods:
Proposition 3.1 Let 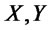 be correlated
be correlated 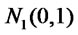 random variables. Let
random variables. Let 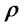 denote the correlation coefficient,
denote the correlation coefficient, 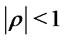 , and
, and 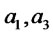 and
and 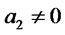 real numbers. Then the random variable
real numbers. Then the random variable
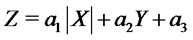
is a mixture of two skew-normally distributed random variables. Specifically, denoting by 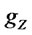 the probability density of
the probability density of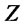 , it holds:
, it holds:
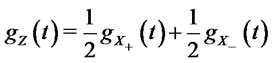
where
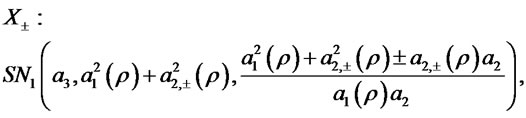
with 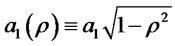 and
and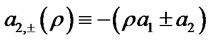 .
.
In particular for 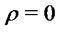 we have:
we have:
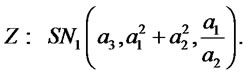
For example it is readily seen that for 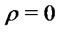 the above result implies:
the above result implies:
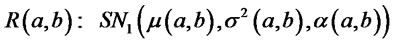 (8)
(8)
with parameters:
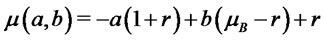 (9)
(9)
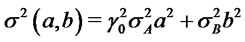 (10)
(10)
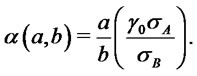 (11)
(11)
We remark that given 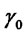 and the assets volatilities
and the assets volatilities 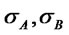 the shape parameter depends only on the ratio of the chosen allocation percentages and vanishes for
the shape parameter depends only on the ratio of the chosen allocation percentages and vanishes for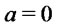 . Shorting the straddle or the second asset produces portfolios with negative shape parameter in the returns distribution and hence with negative skewness. On the other hand positive skewness increases unboundedly as the percentage
. Shorting the straddle or the second asset produces portfolios with negative shape parameter in the returns distribution and hence with negative skewness. On the other hand positive skewness increases unboundedly as the percentage 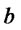 approaches zero. Furthermore, for the above portfolios returns distributions scale and shape parameters satisfy the relation
approaches zero. Furthermore, for the above portfolios returns distributions scale and shape parameters satisfy the relation 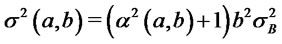 , which implies that scale changes with shape. In the case
, which implies that scale changes with shape. In the case 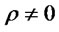 the returns
the returns 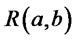 will be described, accordingly to the previous proposition, by a mixture of two skew-normal distributions
will be described, accordingly to the previous proposition, by a mixture of two skew-normal distributions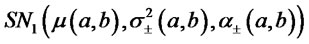 , the identification of
, the identification of 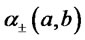 and
and 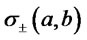 being straightforward. We remark that while on one hand finite mixture of normaldistributions have been already considered in the financial literature as possible flexible tool for modelling assets returns in portfolio selection problems (Buckley et al. ([23])), on the other hand finite mixture of skewnormal distributions up to now have received attention mainly in applied statistical settings, see for instance Lee et al. ([24]), but not in connection with financial applications.
being straightforward. We remark that while on one hand finite mixture of normaldistributions have been already considered in the financial literature as possible flexible tool for modelling assets returns in portfolio selection problems (Buckley et al. ([23])), on the other hand finite mixture of skewnormal distributions up to now have received attention mainly in applied statistical settings, see for instance Lee et al. ([24]), but not in connection with financial applications.
An immediate consequence of the example discussed above is the fact that even in a normal market an investor can face the problem of comparing portfolios having returns which are skew-normally distributed. Once again the decision maker needs criteria which can help her allocation choice process by discarding portfolios which have dominated returns. In the next section we shall provide some simple, yet rigorous, stochastic dominance criteria.
4. Stochastic Dominance Results
We start recalling some basic definitions: given two realvalued random variables  and
and 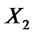 we say that
we say that 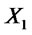 stochastically dominates at first order
stochastically dominates at first order 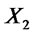 (FSD), and we shortly write
(FSD), and we shortly write 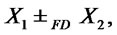 if
if
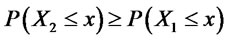 (12)
(12)
for all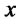 ; we say that
; we say that 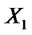 stochastically dominates at second order
stochastically dominates at second order 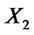 (SSD), and we shortly write
(SSD), and we shortly write 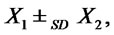 if
if
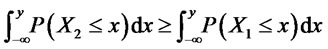 (13)
(13)
for all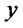 . More generally, a random variable
. More generally, a random variable 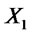 stochastically dominates another random variable
stochastically dominates another random variable 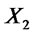 at the order n-th if
at the order n-th if
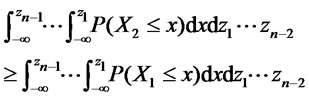
for all values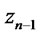 . If the previous inequalities hold strictly we say that we have strict dominance. Obviously (n − 1)-th order dominance implies n-th order dominance.
. If the previous inequalities hold strictly we say that we have strict dominance. Obviously (n − 1)-th order dominance implies n-th order dominance.
The classical stochastic ordering results for univariate normal random variables 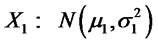 and
and 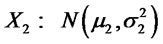 are the following (ref. Levy (2005)):
are the following (ref. Levy (2005)):
1) If 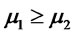 and
and 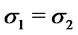 then
then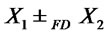 ;
;
2) If 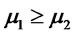 and
and 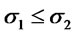 then
then 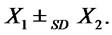
In particular we have strict dominance for 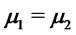 and
and 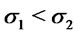 (or
(or 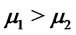 and
and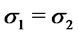 ).
).
To provide a generalization of these results to the skewnormal case we need the following:
Theorem 4.1:
1) Let 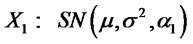 and
and
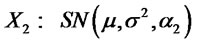 . Suppose
. Suppose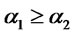 , then
, then
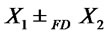 .
.
2) Let 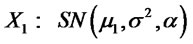 and
and 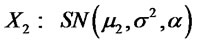 . Suppose
. Suppose 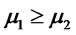 then
then
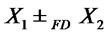 .
.
3) Let 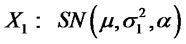 and
and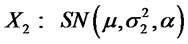 . Suppose
. Suppose 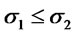 and
and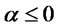 , then
, then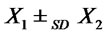 .
.
4) Let 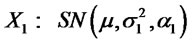 and
and 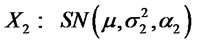 . Suppose
. Suppose 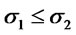 and
and
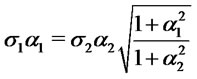 , then
, then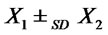 .
.
Proof.
1) Let  and denote by
and denote by 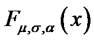 the corresponding distribution function. For each fixed
the corresponding distribution function. For each fixed 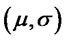 and
and 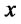 and arbitrary
and arbitrary 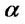 we consider the function
we consider the function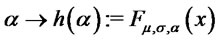 . We have:
. We have:
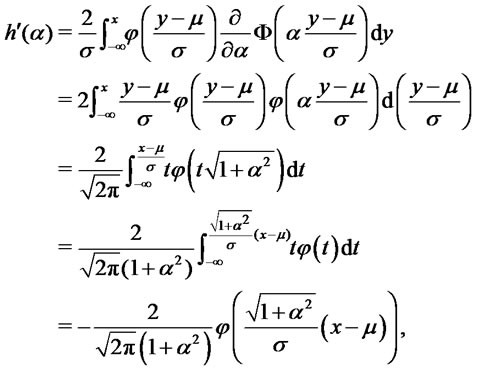
where we have used 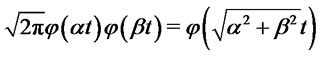
and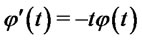 . Therefore
. Therefore 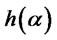 is decreasing and
is decreasing and  for all
for all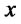 .
.
2) For each fixed 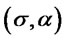 and
and 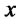 and arbitrary
and arbitrary 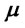 we consider the function
we consider the function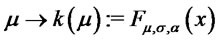 . We have:
. We have:
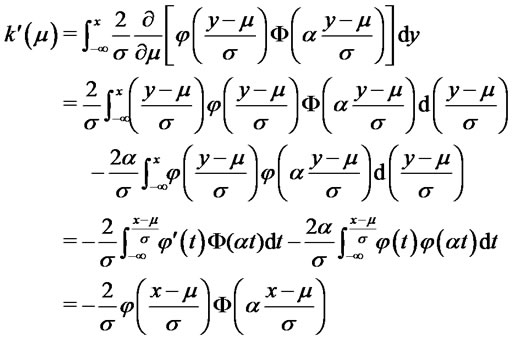
by integrating by parts the first of the two integrals.
Therefore 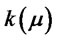 is decreasing and
is decreasing and 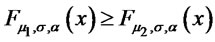 for all
for all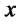 .
.
3) For each fixed 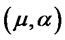 and
and 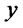 and arbitrary
and arbitrary 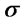 we consider the function
we consider the function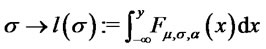 . We have:
. We have:
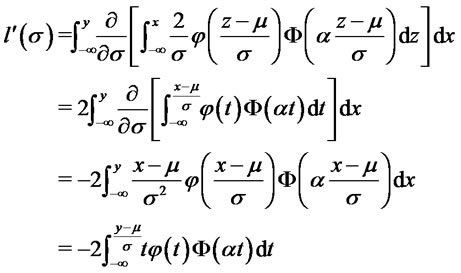
and by integrating by parts the last integral

which is non negative for all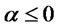 .
.
Henceforth 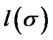 is increasing,
is increasing,
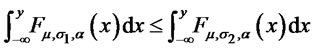 for all
for all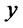 , and we get the result.
, and we get the result.
4) Set 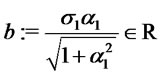 then
then 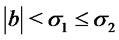 and the second assumption on the parameters is equivalent to
and the second assumption on the parameters is equivalent to
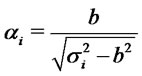 for
for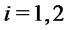 . For each fixed
. For each fixed  and
and 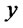
and arbitrary 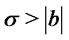 we consider the function
we consider the function 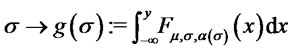 , where
, where
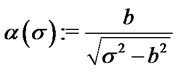 . We have:
. We have:
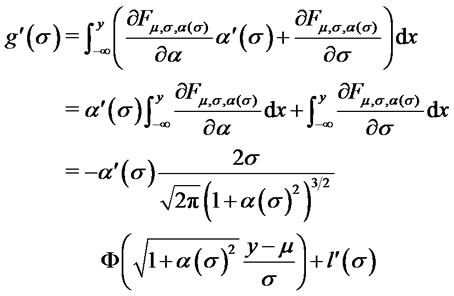
Now , hence:
, hence:
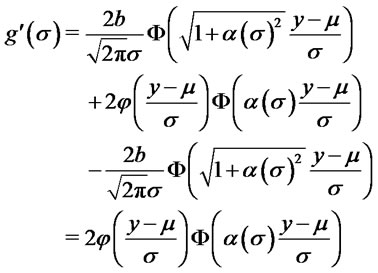
which is non negative. Henceforth 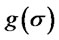 is increasing for all
is increasing for all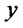 .
.
Remark: The argument by which the result (3) has been obtained fails for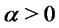 . In such a case
. In such a case 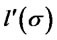 is given by the difference of two positive quantities. The difference is positive for
is given by the difference of two positive quantities. The difference is positive for 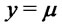 since
since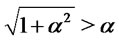 . On the contrary for values of
. On the contrary for values of 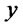 much larger than
much larger than 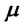 the difference is negative since the first quantity becomes much smaller than the second one. Therefore for positive
the difference is negative since the first quantity becomes much smaller than the second one. Therefore for positive 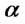 the sign of
the sign of 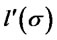 is going to depend on the values of the variable
is going to depend on the values of the variable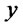 .
.
Corollary 4.2:
1) Let 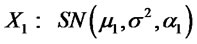 and
and
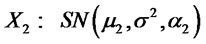 . Suppose
. Suppose 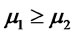 and
and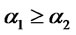 then
then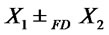 .
.
2) Let 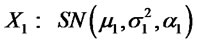 and
and
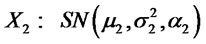 . Suppose
. Suppose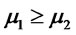 ,
, 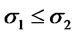 and
and
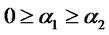 , then
, then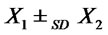 .
.
3) Let  and
and
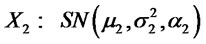 . Suppose
. Suppose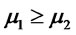 ,
, 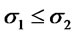 and
and
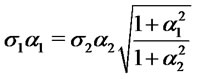 , then
, then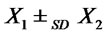 .
.
Proof.
1) Let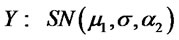 , then by lemma 2.1 (i) and (2) we have:
, then by lemma 2.1 (i) and (2) we have: 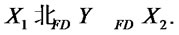
2) Let 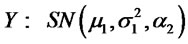 and
and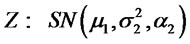 then by lemma 2.1 (1), (2) and (3) we have:
then by lemma 2.1 (1), (2) and (3) we have: 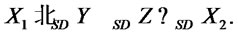
3) Let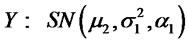 , then by lemma 2.1 (2)
, then by lemma 2.1 (2)
and (4) we have: 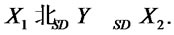
Remark: a) The condition appearing in Corollary 4.2 (3) can be better understood by noticing that is equivalent to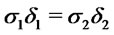 . Therefore the result can be restated in the following form: If
. Therefore the result can be restated in the following form: If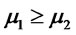 ,
, 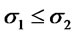 and
and 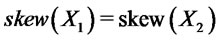 then
then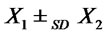 .
.
b) Let 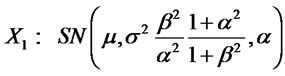 and
and
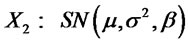 with
with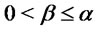 . Being
. Being 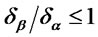 we have
we have 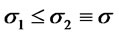 and from Corollary 4.2 (3) it follows
and from Corollary 4.2 (3) it follows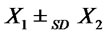 . Notice that
. Notice that
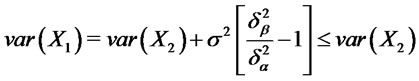 .
.
Henceforth, a larger positive skewness parameter in a financial position gives rise to an improvement over a previous position, from a stochastic dominance viewpoint, if it is accompanied by a variance reduction which leaves unchanged the skewness of the position.
c) It is well known that 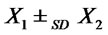 if and only if
if and only if 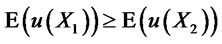 for all non decreasing and concave functions
for all non decreasing and concave functions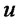 . Therefore, by choosing
. Therefore, by choosing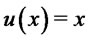 , conditions (2) of Corollary 4.2 imply
, conditions (2) of Corollary 4.2 imply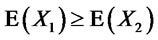 .
.
d) Consider the two-dimensional risky market discussed in Section 2 and the parametrized family of portfolios which invest on the straddle on asset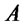 , on shares of asset
, on shares of asset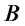 , putting all the remaining wealth on a riskfree bond. Assume
, putting all the remaining wealth on a riskfree bond. Assume 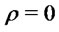 and
and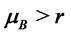 . Consider two portfolios
. Consider two portfolios 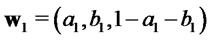 and
and 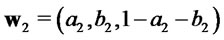 and the corresponding returns
and the corresponding returns 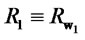 and
and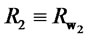 . Suppose 1)
. Suppose 1)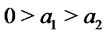 , 2)
, 2)
 , and 3)
, and 3)
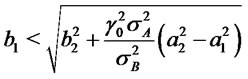 , then from (2) we get
, then from (2) we get
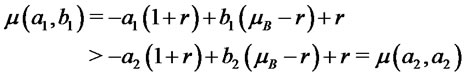 .
.
In addition from (3) we obtain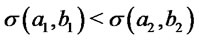 . Finally from (1) we have
. Finally from (1) we have 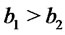 and therefore
and therefore 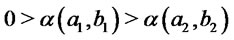 Then by Corollary 4.2 (2) we get
Then by Corollary 4.2 (2) we get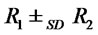 .
.
5. Acknowledgements
The authors thank the anonymous referee for useful suggestions which led to improvements in the presentation of the results. The second named author thanks Prof. A. Ramponi for advices and Centro V. Volterra for financial support.
NOTES