Exponential Ergodicity and β-Mixing Property for Generalized Ornstein-Uhlenbeck Processes ()
1. Introduction
Many continuous time processes are suggested and studied as a natural continuous time generalization of a random recurrence equation, for example, diffusion model of Nelson [2], continuous time GARCH (COGARCH) (1,1) process of Klüppelberg et al. [3] and Lévy-driven Ornstein-Uhlenbeck (OU) process of Barndorff-Nielsen and Shephard [4] etc. Continuous time processes are particularly appropriate models for irregularly spaced and high frequency data [5]. We consider the generalized Ornstein-Uhlenbeck (GOU) process 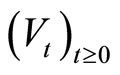 which is defined by
which is defined by
 (1)
(1)
where  is a two-dimensional Lévy process and the starting random variable
is a two-dimensional Lévy process and the starting random variable  is independent of
is independent of . Lévy processes are a class of continuous time processes with independent and stationary increments and continuous in probability. Since Lévy processes
. Lévy processes are a class of continuous time processes with independent and stationary increments and continuous in probability. Since Lévy processes  and
and  are semimartingales, stochastic integral in Equation (1) is well defined.
are semimartingales, stochastic integral in Equation (1) is well defined.
The GOU process is a continuous time version of a stochastic recurrence equation derived from a bivariate Lévy process (de Haan and Karandikar [1]). The GOU process has recently attracted attention, especially in the financial modelling area such as option pricing, insurance and perpetuities, or risk theory. Stationarity, moment condition and autocovariance function of the GOU process are studied in Lindner and Maller [6]. Fasen [7] obtain the results for asymptotic behavior of extremes and sample autocovariance function of the GOU process. For related results, we may consult, e.g. Masuda [8], Klüppelberg et al. [3,9], Maller et al. [5] and Lindner [10] etc.
Mixing property of a stochastic process describes the temporal dependence in data and is used to prove consistency and asymptotic normality of estimators. For a stationary process  and
and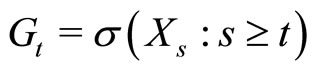 , let
, let

where the supremum takes over 

if  and
and . If
. If  as
as , then
, then  is called β-mixing.
is called β-mixing.  is called exponentially β-mixing if
is called exponentially β-mixing if  for some
for some  and all
and all .
.
In this paper we prove the exponential ergodicity and exponentially β-mixing property of the GOU process
 of Equation (1) and obtain the β-mixing property of the Lévy-driven OU process as a special case.
of Equation (1) and obtain the β-mixing property of the Lévy-driven OU process as a special case.
For more information on Markov chain theory, we refer to Meyn and Tweedie [11]. We refer to Bertoin [12] and Sato [13] for basic results and representations concerning Lévy processes.
2. Exponential Ergodicity of 
2.1. The Model
A bivariate Lévy process 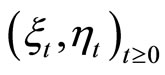 defined on a complete probability space
defined on a complete probability space 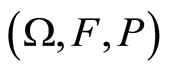 is a stochastic process in
is a stochastic process in , with càdlàg paths,
, with càdlàg paths,  and stationary independent increments, which is continuous in probability.
and stationary independent increments, which is continuous in probability.
Consider the GOU process 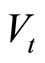 given by
given by

Assume that  is independent of
is independent of . Let
. Let
 (2)
(2)
Then we have that
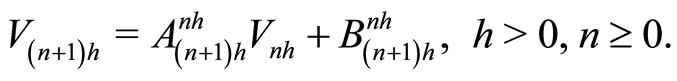 (3)
(3)
Let n denote an integer and  a real number. We can easily show that
a real number. We can easily show that  in Equation (2) is a sequence of independent and identically distributed random vectors and
in Equation (2) is a sequence of independent and identically distributed random vectors and 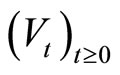 in Equation (1) is a time homogeneous Markov process with t-step transition probability function
in Equation (1) is a time homogeneous Markov process with t-step transition probability function

where 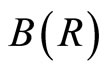 is a Borel σ-field of subsets of real numbers R.
is a Borel σ-field of subsets of real numbers R.
We temporally assume that  is fixed.
is fixed. 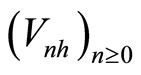 in Equation (3) can be considered as a discrete time Markov process with n-step transition probability function
in Equation (3) can be considered as a discrete time Markov process with n-step transition probability function .
.  is called the h-skeleton chain of
is called the h-skeleton chain of . A Markov process
. A Markov process  is
is 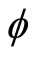 -irreducible if, for some
-irreducible if, for some  -finite measure
-finite measure ,
,  for all
for all  whenever
whenever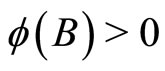 .
. 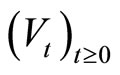 is said to be simultaneously
is said to be simultaneously  -irreducible if any h-skeleton chain is
-irreducible if any h-skeleton chain is  -irreducible. It is known that if
-irreducible. It is known that if  is simultaneously
is simultaneously  -irreducible, then any h-skeleton chain is aperiodic (Proposition 1.2 of Tuominen and Tweedie [14]).
-irreducible, then any h-skeleton chain is aperiodic (Proposition 1.2 of Tuominen and Tweedie [14]).
For fixed , we make the following assumptions:
, we make the following assumptions:
(A1)  and
and .
.
(A2)  for some
for some 
Theorem 2.1 Under the assumption (A1),  defined by Equation (3) converges in distribution to a probability measure
defined by Equation (3) converges in distribution to a probability measure  which does not depend on
which does not depend on . Further,
. Further,  is the unique invariant initial distribution for
is the unique invariant initial distribution for .
.
Proof. The conclusion follows from Theorem 3.1 and Theorem 3.4 in de Haan and Karandikar [1]. Note that if the assumption (A1) holds, then it is obtained that
 and
and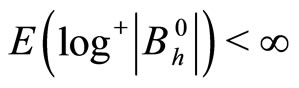 .
.
Remark 1 Assume that . Then
. Then  is also necessary for the existence of a strictly stationary solution. (See Theorem 2.1 in Lindner and Maller [6].)
is also necessary for the existence of a strictly stationary solution. (See Theorem 2.1 in Lindner and Maller [6].)
Remark 2 Suppose that there exist  and
and 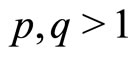 with
with  such that
such that

where  denotes the Lévy exponent of the Lévy process
denotes the Lévy exponent of the Lévy process :
:  If in addition,
If in addition,  then assumptions (A1) and (A2) hold (Proposition 4.1 in Lindner and Maller [6]).
then assumptions (A1) and (A2) hold (Proposition 4.1 in Lindner and Maller [6]).
2.2. Drift Condition for 
A discrete time Markov process 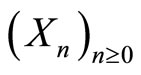 is said to hold the drift condition if there exist a positive function g on R, a compact set K, and constants
is said to hold the drift condition if there exist a positive function g on R, a compact set K, and constants 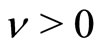 and
and  such that
such that

and 
Theorem 2.2 Under the assumptions (A1) and (A2),  given in Equation (3) satisfies the drift condition.
given in Equation (3) satisfies the drift condition.
Proof. For notational simplicity, let . From assumptions, we have that
. From assumptions, we have that  and
and  for some
for some . Then
. Then

as  ( Hardy et al. [15]). Here
( Hardy et al. [15]). Here  implies the existence of
implies the existence of ,
, 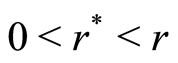 such that
such that . Now define a nonnegative test function g on R by
. Now define a nonnegative test function g on R by . Then we have that
. Then we have that
 (4)
(4)
where , by assumption (A2). Since
, by assumption (A2). Since  increases to
increases to 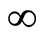 as
as  increases to
increases to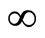 , for any
, for any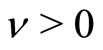 , there exist
, there exist 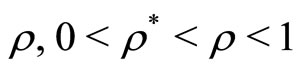 and
and  with
with , such that
, such that
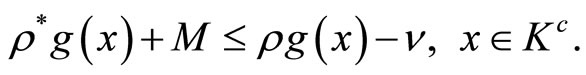 (5)
(5)
Clearly,
 (6)
(6)
Combining Equations (4)-(6), the drift condition for  holds.
holds.
2.3. Simultaneous  -Irreducibility of
-Irreducibility of 
For reader’s convenience, we state the following theorems which play important roles to prove our main results.
Theorem 2.3 (Meyn and Tweedie [11]) Suppose that a Markov chain  has the Feller property. If
has the Feller property. If  satisfies the drift condition for a compact set
satisfies the drift condition for a compact set
 , then there exists an invariant probability measure. In addition, if the process is
, then there exists an invariant probability measure. In addition, if the process is  -irreducible and aperiodic, then the given process is geometrically ergodic.
-irreducible and aperiodic, then the given process is geometrically ergodic.
Theorem 2.3 shows that the crucial step to prove the geometric ergodicity of a Markov process is to show that the given process is  -irreducible and holds the drift condition. In many cases, however, proving irreducibility of a Markov process is an awkward task. Consulting the following Theorem 2.4, irreducibility of the process can be derived from connection between
-irreducible and holds the drift condition. In many cases, however, proving irreducibility of a Markov process is an awkward task. Consulting the following Theorem 2.4, irreducibility of the process can be derived from connection between  -irreducibility and the uniform countable additivity condition. A Markov chain
-irreducibility and the uniform countable additivity condition. A Markov chain  is said to hold the uniform countable additivity condition (Liu and Susko [16]) if its one-step transition probability function satisfies that for any decreasing sequence
is said to hold the uniform countable additivity condition (Liu and Susko [16]) if its one-step transition probability function satisfies that for any decreasing sequence 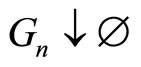 inside compact sets,
inside compact sets,

Theorem 2.4 (Tweedie [17]) Suppose that the drift condition holds with a test set K and the uniform countable additivity condition holds for the same set K. Then there is a unique invariant measure for  if and only if
if and only if  is
is  -irreducible.
-irreducible.
Let  be the compact set defined in the proof of Theorem 2.2.
be the compact set defined in the proof of Theorem 2.2.
Theorem 2.5 Under the assumptions (A1) and (A2),  is simultaneously π-irreducible if for any
is simultaneously π-irreducible if for any ,
,
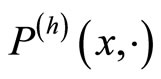 has a probability density function
has a probability density function 
(with respect to the Lebesgue measure ), which is uniformly bounded on compacts for
), which is uniformly bounded on compacts for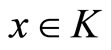 .
.
Proof. Let  be any decreasing sequence inside compact sets with
be any decreasing sequence inside compact sets with . Then
. Then
 (7)
(7)
where  .
.
The inequality in Equation (7) and the condition that  is any sequence inside compact sets in
is any sequence inside compact sets in  with
with  imply that
imply that
 .
.
Therefore the uniform countable additivity condition holds for the compact set K. Theorem 2.4 and the existence of a unique invariant initial distribution for
 yield the
yield the  -irreducibility of any h-skeleton chain
-irreducibility of any h-skeleton chain .
.
To complete the proof, we need to show that the assumption (A1) and (A2) hold for all . Since Lévy processes have stationary and independent increments, it is easy to show that the assumption (A1) and
. Since Lévy processes have stationary and independent increments, it is easy to show that the assumption (A1) and 
hold for all . It remains to prove that
. It remains to prove that

for all 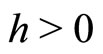 with some
with some . We first define a finite Lévy process
. We first define a finite Lévy process  as follows:
as follows:

Then it is shown that ,
,

(See Proposition 2.3 in Lindner and Maller [6]). Without loss of generality, we may assume that . Choose any
. Choose any . Then
. Then , where n is a nonnegative integer,
, where n is a nonnegative integer,  and
and 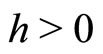 is in the assumptions (A1) and (A2), we have that
is in the assumptions (A1) and (A2), we have that
 (8)
(8)
The first inequality in Equation (8) follows from stationary and independent increments property of Lévy processes  and
and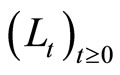 .
.
Therefore for any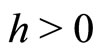 , h-skeleton chain
, h-skeleton chain  is
is  -irreducible and hence
-irreducible and hence 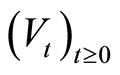 is simultaneously
is simultaneously  -irreducible and
-irreducible and  is aperiodic.
is aperiodic.
2.4. Exponential Ergodicity of 
The next theorem is our main result.
Theorem 2.6 Suppose that the assumptions of Theorem 2.5 hold. Then the GOU process  in Equation (1) is exponentially ergodic and holds the exponentially
in Equation (1) is exponentially ergodic and holds the exponentially  -mixing property.
-mixing property.
Proof. Theorem 2.5 shows that any h-skeleton chain
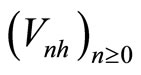 is
is  -irreducible and aperiodic. Note that
-irreducible and aperiodic. Note that  is a Feller chain, that is,
is a Feller chain, that is, 
is a continuous function of x whenever f is continuous and bounded. Therefore any nontrivial compact set is a small set. Theorem 2.2 ensures that  holds the drift condition and hence Theorem 2.5 and Theorem 2.3 imply that
holds the drift condition and hence Theorem 2.5 and Theorem 2.3 imply that  is geometrically ergodic, that is, there exists a constant
is geometrically ergodic, that is, there exists a constant  such that
such that
 (9)
(9)
 -a.a. x as
-a.a. x as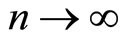 , where
, where 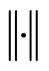 denotes the total variation norm. Under simultaneous
denotes the total variation norm. Under simultaneous 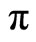 -irreducibility condition of
-irreducibility condition of , Equation (9) and Theorem 5 in Tuominen and Tweedie [14] guarantee the exponential ergodicity of
, Equation (9) and Theorem 5 in Tuominen and Tweedie [14] guarantee the exponential ergodicity of  in the following sense:
in the following sense:

as , for some
, for some  and
and  -a.a. x.
-a.a. x.  -mixing property for the continuous time GOU process
-mixing property for the continuous time GOU process  is also obtained.
is also obtained.
2.5. Examples
In this example, we assume that . If
. If 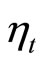 is any Lévy process, then
is any Lévy process, then  in Equation (1) is the Lévydriven OU process which is studied by Barndorff-Nielsen and Shephard [4]. In particular, if
in Equation (1) is the Lévydriven OU process which is studied by Barndorff-Nielsen and Shephard [4]. In particular, if  is a subordinator, that is,
is a subordinator, that is,  has nondecreasing sample path, finite variation with nonnegative drift and Lévy measure concentrated on
has nondecreasing sample path, finite variation with nonnegative drift and Lévy measure concentrated on , then
, then  is called the Lévy-driven stochastic volatility model. For the case that
is called the Lévy-driven stochastic volatility model. For the case that  is a Brownian motion,
is a Brownian motion,  is the classical OU process. Let
is the classical OU process. Let  be the Lévy measure for the process
be the Lévy measure for the process  and assume that
and assume that 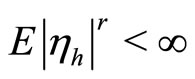 for some
for some  and
and .
.
Then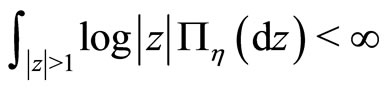 . Here we can easily show that the assumptions (A1)and (A2) hold. Theorem 2.2 implies that
. Here we can easily show that the assumptions (A1)and (A2) hold. Theorem 2.2 implies that  holds the drift condition. Moreover, it is known that
holds the drift condition. Moreover, it is known that  admits a
admits a  density
density  for each
for each  (Sato and Yamazato [18]) and by Theorem 2.5,
(Sato and Yamazato [18]) and by Theorem 2.5,  is
is 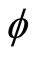 -irreducible. Above statements hold for any
-irreducible. Above statements hold for any 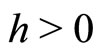 and hence
and hence 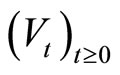 is simultaneously
is simultaneously  -irreducible. Therefore exponential ergodicity and exponential
-irreducible. Therefore exponential ergodicity and exponential  -mixing property of
-mixing property of  follow from Theorem 2.6.
follow from Theorem 2.6.
3. Conclusion
Recently, time series models in finance and econometrics are suggested as continuous time models which are particularly appropriate for irregularly spaced and high frequency data. The GOU process is a continuous time stochastic process driven by a bivariate Lévy process. The stationarity, moment conditions, autocovariance function and asymptotic behavior of extremes of the process are studied in [6,7], but exponential ergodicity does not seem to have been investigated as yet. In this paper, we give sufficient conditions under which the process is exponentially ergodic and  -mixing. The drift condition and the simultaneous
-mixing. The drift condition and the simultaneous  -irreducibility of the process that is induced from uniform countable additivity condition play a crucial role to prove the results. Our results are used to show, in particular, consistency and asymptotic normality of estimators.
-irreducibility of the process that is induced from uniform countable additivity condition play a crucial role to prove the results. Our results are used to show, in particular, consistency and asymptotic normality of estimators.
4. Acknowledgements
This research was supported by KRF grant 2010- 0015707.