Study of Decoherence of Elementary Gates Implemented in a Chain of Few Nuclear Spins Quantum Computer Model ()
1. Introduction
Most of the ideal quantum insulated systems exist only in our mind, where one considers that environment has not interaction with the quantum system. However, in the real world the interaction of the system with the environment is almost unavoidable. In principle, one could study the unitary evolution of the whole system: quantum plus environment and their interaction, but this situation represents a many bodies problem which is unsolvable within any picture of the quantum mechanics. There are two approaches to attack this problem. The first one consists on to look for the phenomenological classical dissipative system and to get its associated Hamiltonian, then to proceed to do the usual quantization of the system [1, 2]. The other one, which it is more fundamental, uses the matrix density approach for the whole system and makes the trace over the environment variables [3-11]. The resulting density matrix is called “reduced density matrix”, and its associated non-unitary evolution equation is called “master equation”. This equation is also phenomenological one, and it has defined a dissipative and diffusion parameters which can (non Markovian process) or can not (Markovian process) depend on the time evolution of the system [3-17]. These parameters are responsible for the decay behavior of the non diagonal matrix elements of the reduced density matrix. This phenomenon is called “decoherence” because is related also with the disappearance of the interference terms of the product of the quantum wave function [19]. In addition, this decoherence phenomena could have an important relation with the appearance of the classical world [18-23]. Unfortunately, there is not a general unique master equation which could be used for any quantum system in interaction with the environment, and there is not a unified consensus about the best approach for studying a given quantum system interacting with the environment and/or the measurement apparat [3]. Additionally, the environment can be taken as bosonic [24-29] or fermionic [27], and the interaction between quantum and environment system is taken as a constant force (the potential is just the product of the variables of the quantum system with the environment system). In most of the approaches, the positiveness and trace equal to one are kept as principal condition for the reduced density matrix. The best known mathematical approach which kept these conditions was given by Lindblad [3,4], which gave an abstract general non unitary evolution equation for the reduced density matrix. The master equation is different when dealing with continuos systems (quantum Browning motion, for example) [5,6] or discrete quantum systems (spin system) [3,26]. One of the used approaches for quantum discrete system is described in [30], where it was used for studying sudden death of entanglement of two qubits. We will use this approach for our study of decoherence of several quantum gates during operation in a quantum computer model made up of a linear chain of three paramagnetic atoms with nuclear spin one half [31,34,36]. In this work, we are interested in determine the decoherence of a single qubit rotation, quantum controlled-not (CNOT), and quantum controlled-controllednot (C2NOT) gates during their implementation on this quantum computer model.
We describe the model and the Hamiltonian of our quantum system, and we must point out that, although this Hamiltonian will be time explicitly dependent, if we consider weak interaction between our system and the environment (the characteristic times of the quantum system are much longer than those of the environment) as a first approximation, the above mentioned Markovian-Lindblad master type equation can be still used for our study [3,32,33]. On the other hand, even this model for solid state quantum computer has not been built yet, it has been very useful for theoretical studies about implementation of quantum gates and quantum algorithms [34-36] which can be extrapolated to other solid state quantum computers [37-39].
2. Hamiltonian of the System
The Hamiltonian that describes the ideal insulated system of a linear chain of N paramagnetic atoms with nuclear spin one half inside the magnetic field
 (1)
(1)
where 
 and
and  are the amplitude, the angular frequency and the phase of the RF-field, and
are the amplitude, the angular frequency and the phase of the RF-field, and  represents the amplitude of the z-component of the magnetic field, is given by (see [31,34])
represents the amplitude of the z-component of the magnetic field, is given by (see [31,34])
 (2)
(2)
where  represent the magnetic moment of the kthnucleus, which it is given in terms of the nuclear spin as
represent the magnetic moment of the kthnucleus, which it is given in terms of the nuclear spin as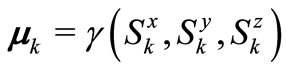 , with
, with  being the proton gyromagnetic ratio and
being the proton gyromagnetic ratio and  being the jth-component of the spin operator,
being the jth-component of the spin operator,  represents the magnetic field, Equation (1) valuated at the location of the kth-nuclear spin (
represents the magnetic field, Equation (1) valuated at the location of the kth-nuclear spin ( ). The parameters
). The parameters 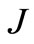 and
and  represent the coupling constant at first and second neighbor interaction. The angle between the linear chain and the z-component of the magnetic field is chosen as
represent the coupling constant at first and second neighbor interaction. The angle between the linear chain and the z-component of the magnetic field is chosen as  to eliminate the dipole-dipole interaction between the spins.
to eliminate the dipole-dipole interaction between the spins.
This Hamiltonian can be written as
 (3)
(3)
where H0 and W are defined as
 (4)
(4)
and
 (5)
(5)
where we have used the relation , with the operator
, with the operator  written in terms of Pauli matrixes as
written in terms of Pauli matrixes as . Here we have that:
. Here we have that:  is the Larmor frequency of the kth-spin,
is the Larmor frequency of the kth-spin,  is the Rabi frequency, and
is the Rabi frequency, and 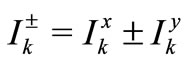 represents the ascend operator (
represents the ascend operator ( ) or the descend operator (
) or the descend operator (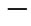 ). The Hamiltonian
). The Hamiltonian  is diagonal in the basis
is diagonal in the basis 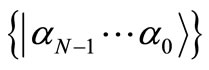 with
with  (zero for the ground state and one for the exited state). The action of the spin operators on its respective qubit is given by
(zero for the ground state and one for the exited state). The action of the spin operators on its respective qubit is given by ,
,  , and
, and . The eigenvalues of
. The eigenvalues of 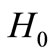 in this basis are given by
in this basis are given by
 (6)
(6)
The elements of this basis forms a register of N-qubits with a total number of  registers which is the dimensionality of our Hilbert space. The allowed transition of one state to another one is gotten by choosing the angular frequency of the RF-field,
registers which is the dimensionality of our Hilbert space. The allowed transition of one state to another one is gotten by choosing the angular frequency of the RF-field,  , as the associated angular frequency due to the energy difference of these two levels, and by choosing the normalized evolution time
, as the associated angular frequency due to the energy difference of these two levels, and by choosing the normalized evolution time  with the proper time duration (so called RF-field pulse). The set of selected pulses defines the quantum gate we want to study with this quantum computer.
with the proper time duration (so called RF-field pulse). The set of selected pulses defines the quantum gate we want to study with this quantum computer.
3. System-Environment Interaction Models
Now, to deal with the non ideal situation where the effect of the environment is taken into account, we make use of the Lindblad type master equation for the evolution of the reduced density matrix
 (7)
(7)
where the first part on the right side denotes the usual von Neuman unitary evolution of the reduced density matrix, and the second term represents the Lindblad part (non unitary) evolution. This second term has different expression for different consideration of the system-environment interaction. For the qubits interacting independently with the environment (case (A)), this term has the following form [30]
 (8)
(8)
where  is the dissipative parameter associated to the jth-qubit.
is the dissipative parameter associated to the jth-qubit.
For the pure dephasing interaction case, where the qubits independently dephase to their respective bath with a dephasing rate , the Lindblad term is given by
, the Lindblad term is given by
 (9)
(9)
For the independent-qubit-correlated case (qubits interact with the environment collectively), the Lindblad operator is written as
 (10)
(10)
where one has that 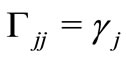 is the decay rate of case (A). In this case, the decay of the state of a qubit has an effect on the other qubits.
is the decay rate of case (A). In this case, the decay of the state of a qubit has an effect on the other qubits.
For the qubit-correlated and dephasing case, with  as the decay rate of the correlated dephasing, the Lindblad operator is given by
as the decay rate of the correlated dephasing, the Lindblad operator is given by
 (11)
(11)
In this case, the decay of one qubit affects too the other qubits.
The dynamical system for each case for the reduced density matrix elements is deduced from Equation (7) as
 (12)
(12)
where  and
and  represent the elements of the basis of the Hilbert space,
represent the elements of the basis of the Hilbert space,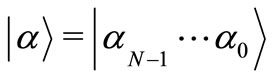 and
and and naming the ground state
and naming the ground state  as the first state of the system. In our case, one has that
as the first state of the system. In our case, one has that , the dimensionality of our Hilbert space is eight, and the explicit equations for the dynamical system of each case are given in the appendix.
, the dimensionality of our Hilbert space is eight, and the explicit equations for the dynamical system of each case are given in the appendix.
4. Simulation Results
Our registers are made up of three qubits  with
with , or written them with decimal notation,
, or written them with decimal notation,  ,
,  and so on (do not confuse with the type of environment). The parameters used for our simulation are taken from [36] and are given (in units of
and so on (do not confuse with the type of environment). The parameters used for our simulation are taken from [36] and are given (in units of ) as
) as
 (13)
(13)
Using the assumption that the environment acts homogeneously on the qubits, the damping parameter can be the same for each qubit, and the damping parameter for correlated cases at second neighbors can be one order of magnitude weaker that at first neighbors. Thus, the dissipative coefficients appearing for the cases (A), (B), (C), and (D) are taken of the following way
 (14)
(14)
where  is the free common parameter which takes into account the interaction with the environment. The reduced density matrix is then made up of 8 × 8 complex elements, and if the initial state is always taken as the ground state of the quantum state
is the free common parameter which takes into account the interaction with the environment. The reduced density matrix is then made up of 8 × 8 complex elements, and if the initial state is always taken as the ground state of the quantum state , this means that the initial reduced density matrix has the values
, this means that the initial reduced density matrix has the values  and
and 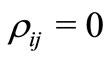 for
for .
.
4.1. Single Qubit Rotation
We have selected the transition 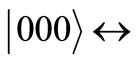 (or in decimal notation:
(or in decimal notation: ) as an example of single qubit rotation (corresponding to the NOT quantum gate), and the NOT-reduced density matrix after a
) as an example of single qubit rotation (corresponding to the NOT quantum gate), and the NOT-reduced density matrix after a  -pulse with resonant frequency
-pulse with resonant frequency  would be such that
would be such that 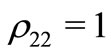 and
and  for
for . In addition, we allow the system to run for almost two an a half
. In addition, we allow the system to run for almost two an a half  -pulses more to see how the NOT gate evolves. Figure 1 shows the decoherence behavior (damping of the non diagonal matrix element
-pulses more to see how the NOT gate evolves. Figure 1 shows the decoherence behavior (damping of the non diagonal matrix element ) for the cases (A), (B), (C) and (D), using different values for the damping parameter. In it, we can see a revival in the coherence with smaller amplitude, which is due to the three and a half pulses applied to the system. The effect of the environment is to reduce the amplitude of the coherent terms involved in the transitions, and to create new superposition of other states. Once enough time has passed, the destruction of the expected superposition will be absolute and new states take the entire probability of the system, like the state related to the element
) for the cases (A), (B), (C) and (D), using different values for the damping parameter. In it, we can see a revival in the coherence with smaller amplitude, which is due to the three and a half pulses applied to the system. The effect of the environment is to reduce the amplitude of the coherent terms involved in the transitions, and to create new superposition of other states. Once enough time has passed, the destruction of the expected superposition will be absolute and new states take the entire probability of the system, like the state related to the element  in Figure 2.
in Figure 2.
The Figure 2 shows the behavior of the diagonal reduced density matrix elements when dissipation is switched on, with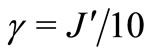 . Since one must have that
. Since one must have that , the damping of the matrix elements
, the damping of the matrix elements 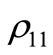 and
and  (destruction of the transition of the states
(destruction of the transition of the states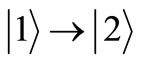 ) brings about the excitation of other matrix elements as shown on left hand side figures. Our simulation also show that the environment generating dephasing, described by cases B and D are less harmful to the system than the environments related to cases (A) and (C). The system interacting with environments B and C has a faster recovery when the dissipation parameter goes weaker.
) brings about the excitation of other matrix elements as shown on left hand side figures. Our simulation also show that the environment generating dephasing, described by cases B and D are less harmful to the system than the environments related to cases (A) and (C). The system interacting with environments B and C has a faster recovery when the dissipation parameter goes weaker.
To characterize the decoherence behavior of the off diagonal element of the reduced density matrix, assume that one defines the decay characteristic parameter as  as the time when the matrix element
as the time when the matrix element  has a value of
has a value of  on the first pulse. Then, Figure 3 shows the dependence of this characteristic parameter as a function of the dissipative parameter
on the first pulse. Then, Figure 3 shows the dependence of this characteristic parameter as a function of the dissipative parameter 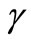 for our four cases. The behavior of this parameter as a function of the dissipative parameter
for our four cases. The behavior of this parameter as a function of the dissipative parameter 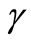 can be fixed by a linear relation,
can be fixed by a linear relation, 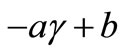
 , where
, where 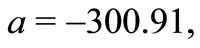
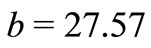 for the independent cases (A) and (C), and
for the independent cases (A) and (C), and 
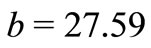 for the dephasing cases (B) and (D).
for the dephasing cases (B) and (D).
Other parameter which can help us to see the departure from the ideal ( ) behavior could be the distance
) behavior could be the distance  between the non diagonal matrix elements
between the non diagonal matrix elements 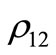 of the ideal (
of the ideal ( ) and the dissipative cases (
) and the dissipative cases (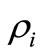 , for
, for ). Figure 4 shows the behavior of this distance for different values of
). Figure 4 shows the behavior of this distance for different values of  indexed by (1)
indexed by (1) , (2)
, (2)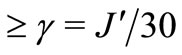 , (3)
, (3)  and (4)
and (4) . Of course, this distance increases as
. Of course, this distance increases as  increases because the decoherence is taking place deeper. The maximum separation corresponds to the maximum on the coherence behavior as shown in Figure 1.
increases because the decoherence is taking place deeper. The maximum separation corresponds to the maximum on the coherence behavior as shown in Figure 1.
4.2. Controlled-Not (CNOT) Quantum Gate
To get the CNOT quantum gate starting from the ground state , one applies a
, one applies a  -pulse between this state and the state
-pulse between this state and the state , with resonant frequency
, with resonant frequency , to get the superposition state
, to get the superposition state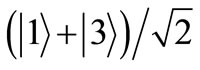 . Then, one applies a resonant
. Then, one applies a resonant  -pulse between the states
-pulse between the states  and
and , with resonant frequency
, with resonant frequency to get the final desired state
to get the final desired state  which means that the expected CNOT density matrix would be such that
which means that the expected CNOT density matrix would be such that , and all the other elements are equal to zero. In addition, one allows the system to have two and a half more resonant
, and all the other elements are equal to zero. In addition, one allows the system to have two and a half more resonant  -pulses to have a better look of the CNOT behavior. Figure 5 shows the decoherence behavior (damping of the non diagonal matrix elements
-pulses to have a better look of the CNOT behavior. Figure 5 shows the decoherence behavior (damping of the non diagonal matrix elements ) for the cases (A), (B), (C) and (D), using different the damping parameters. One observes from these figures that there is not significant difference between independent and correlated-independent, and between dephasing and correlated-dephasing cases (similar behavior is observed for the other non diagonal matrix elements).
) for the cases (A), (B), (C) and (D), using different the damping parameters. One observes from these figures that there is not significant difference between independent and correlated-independent, and between dephasing and correlated-dephasing cases (similar behavior is observed for the other non diagonal matrix elements).
We note the peculiar behavior of the term 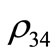 for the cases (A) and (C) of Figure 5, for a relatively high dissipation (labeled (1)). Before this superposition occurs, other elements of the density matrix have already been exited due to the interaction with the environment and the condition of
for the cases (A) and (C) of Figure 5, for a relatively high dissipation (labeled (1)). Before this superposition occurs, other elements of the density matrix have already been exited due to the interaction with the environment and the condition of . So, the other excited states seems to have an important influence to slow the formation of the superposition, characterized by the term
. So, the other excited states seems to have an important influence to slow the formation of the superposition, characterized by the term . As the dissipation parameter goes weaker, a regular behavior is observed. We can also see on Figure 5 that for short times, other states get exited besides the ones involved in the CNOT gate, therefore there are other states also overlapped with the states
. As the dissipation parameter goes weaker, a regular behavior is observed. We can also see on Figure 5 that for short times, other states get exited besides the ones involved in the CNOT gate, therefore there are other states also overlapped with the states  and
and . A revival in the superposition of
. A revival in the superposition of  and
and  can be seen when enough of time has passed so that the other states excited by the environment have also went down (curve labeled with (1)). Figure 6 shows the diagonal reduced density matrix elements with
can be seen when enough of time has passed so that the other states excited by the environment have also went down (curve labeled with (1)). Figure 6 shows the diagonal reduced density matrix elements with , for the four cases into consideration. Cases (A) and (C) shows the increasing of other diagonal matrix elements to keep
, for the four cases into consideration. Cases (A) and (C) shows the increasing of other diagonal matrix elements to keep , corresponding to excitation of the state
, corresponding to excitation of the state .
.
As we observed with the NOT quantum gate before, in our simulations we observed for the CNOT gate that the dependence of the characteristic decay parameter 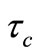 with respect the dissipation parameter
with respect the dissipation parameter  is linear for the non diagonal elements
is linear for the non diagonal elements ,
,  and
and , although their parameters a and b have different values for different non diagonal elements. However, these values are almost the same for the cases (A)-(C) and (B)-(D). In addition, the behavior of the distance
, although their parameters a and b have different values for different non diagonal elements. However, these values are almost the same for the cases (A)-(C) and (B)-(D). In addition, the behavior of the distance 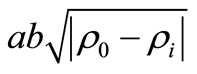 for
for 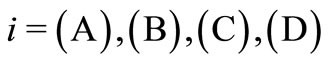 cases for the non diagonal matrix elements is again very similar to that one found for the NOT quantum gate (Figure 5), that is, we observed and increasing of this distance as the dissipation gets stronger.
cases for the non diagonal matrix elements is again very similar to that one found for the NOT quantum gate (Figure 5), that is, we observed and increasing of this distance as the dissipation gets stronger.
4.3. Controlled-Controlled-Not (C2NOT) Quantum Gate
To get the C2NOT quantum gate starting from the ground state , one applies a
, one applies a  -pulse between this state and the state
-pulse between this state and the state  with resonant frequency
with resonant frequency  to get the superposition state
to get the superposition state . Then, one applies a resonant
. Then, one applies a resonant 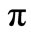 -pulse between the states
-pulse between the states 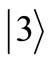 and the state
and the state  with resonant frequency
with resonant frequency  to get the desired superpositional state
to get the desired superpositional state . Finally, C2NOT operation is achieved through a
. Finally, C2NOT operation is achieved through a  pulse between the state
pulse between the state  and the state
and the state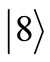 , getting the state
, getting the state . In addition, we allow the system to evolve for another almost two an a half pulses to see the behavior of the C2NOT. The expected C2NOT density matrix would be such that
. In addition, we allow the system to evolve for another almost two an a half pulses to see the behavior of the C2NOT. The expected C2NOT density matrix would be such that  and all the other elements equal to zero. Figure 7 shows the behavior of the non diagonal matrix elements
and all the other elements equal to zero. Figure 7 shows the behavior of the non diagonal matrix elements  for the cases (A), (B), (C) and (D), using different damping parameters. As in the CNOT gate, a similar strange behavior is seen for the coherent terms which appears later in the gate (
for the cases (A), (B), (C) and (D), using different damping parameters. As in the CNOT gate, a similar strange behavior is seen for the coherent terms which appears later in the gate ( and
and ) for the cases (A) and (C) at relatively high
) for the cases (A) and (C) at relatively high
dissipation parameter, that is, the state  is excited for strong dissipation.
is excited for strong dissipation.
Figure 8 shows the diagonal reduced density matrix elements with , for the four cases into consideration. Cases (A) and (C) showing the excitation of other diagonal elements to keep
, for the four cases into consideration. Cases (A) and (C) showing the excitation of other diagonal elements to keep .
.
As for the NOT and CNOT quantum gates, in our simulation we observe a similar expected linear dependence of the characteristic decay parameter 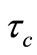 with respect the dissipative parameter
with respect the dissipative parameter  for the non diagonal elements, although the parameters a and b have different values for different non diagonal elements. The behavior of the difference
for the non diagonal elements, although the parameters a and b have different values for different non diagonal elements. The behavior of the difference , between the non diagonal matrix elements of their ideal values
, between the non diagonal matrix elements of their ideal values 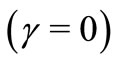 and their dissipative values
and their dissipative values  and for the cases
and for the cases

is again similar as the other gates.
5. Purity Calculations
The purity function,  , is a measure of how close a quantum system is from its description as a pure state quantum system and varies between 1 and
, is a measure of how close a quantum system is from its description as a pure state quantum system and varies between 1 and  (d the dimensionality of the density matrix). This function may decay with the decoherence since the system may move away from an initial pure state. Therefore, this function can be used to characterize the environment. Figure 9 shows the behavior of the purity for the CNOT gate using several dissipative parameters (the behavior of the purity is similar for the NOT and C2NOT quantum gates). As one ca see from these figures, Independent environment is characterized by an initial linear damping (exponential) in the purity function, meanwhile dephasing damping is characterized by an initial quadratic damping (Gaussian) in the purity function. This an be understood because the dephasing case has weaker effect on the decoherence of the system, as can be seen from
(d the dimensionality of the density matrix). This function may decay with the decoherence since the system may move away from an initial pure state. Therefore, this function can be used to characterize the environment. Figure 9 shows the behavior of the purity for the CNOT gate using several dissipative parameters (the behavior of the purity is similar for the NOT and C2NOT quantum gates). As one ca see from these figures, Independent environment is characterized by an initial linear damping (exponential) in the purity function, meanwhile dephasing damping is characterized by an initial quadratic damping (Gaussian) in the purity function. This an be understood because the dephasing case has weaker effect on the decoherence of the system, as can be seen from
Figure 5, where the maximum values reached by the non diagonal matrix density elements are bigger for dephasing case than for independent case. Purity increases its value after the first decay for high damping values ( ) and for the independent case since for this value a particular state is exited (trying to keep
) and for the independent case since for this value a particular state is exited (trying to keep ) as seen in Figure 6.
) as seen in Figure 6.
6. Conclusion
Within the Markov approximation for the study of quantum discrete system with environment, we have solved numerically the master equation for the reduced density matrix associated to our linear chain of three nuclear spin quantum computer interacting with the environment, and we have made the simulation of a particular single qubit transition (NOT gate), CNOT and C2NOT quantum gates operating within this dissipative environment. Within the validity of this approximation, the coherence of these quantum logic gates have been determined, and we have calculated the associated decoherence time (using the first pulse applied to the system), 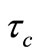 , as a function of a common dissipative parameter (all the dissipative parameters appearing in the Lindblad part of the master equation were chosen proportional a single one), and it was found the expected linear dependence of this coherence time with respect this dissipative parameter, but with different decay rates for the non diagonal matrix elements and gates. The value of the dissipative parameter for the environment not to affect the performance of these quantum gates (within two cycles and a half after their formation) was found to be
, as a function of a common dissipative parameter (all the dissipative parameters appearing in the Lindblad part of the master equation were chosen proportional a single one), and it was found the expected linear dependence of this coherence time with respect this dissipative parameter, but with different decay rates for the non diagonal matrix elements and gates. The value of the dissipative parameter for the environment not to affect the performance of these quantum gates (within two cycles and a half after their formation) was found to be . We used the purity parameter to study its behavior of this chain of three nuclear spin system interacting with the environment, and we have found an initial linear (or exponential) damping of the purity parameter for the independent case, and an initial quadratic (or Gaussian) damping on its behavior for the dephasing case, giving us an indication of strong (linear) or weak (quadratic) effect of the environment in our system. For very strong dissipation, we found that purity may increase because, the condition
. We used the purity parameter to study its behavior of this chain of three nuclear spin system interacting with the environment, and we have found an initial linear (or exponential) damping of the purity parameter for the independent case, and an initial quadratic (or Gaussian) damping on its behavior for the dephasing case, giving us an indication of strong (linear) or weak (quadratic) effect of the environment in our system. For very strong dissipation, we found that purity may increase because, the condition  on the density matrix, sometimes implies strong excitation of other state involved in the dynamics, causing the system to try to return to a pure quantum state description.
on the density matrix, sometimes implies strong excitation of other state involved in the dynamics, causing the system to try to return to a pure quantum state description.
Appendix
The evolution equation for the density matrix elements are given from Equation (12) by
 (X1)
(X1)
Making the following definition
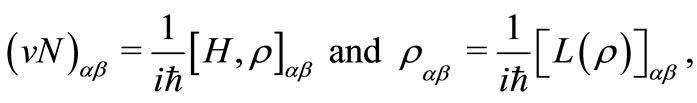 (X2)
(X2)
one gets
Von Neuman (vN) Part
 (V1)
(V1)
 (V2)
(V2)
 (V3)
(V3)
 (V4)
(V4)
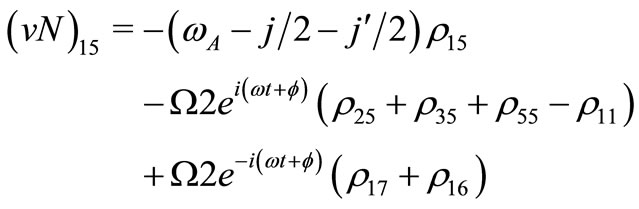 (V5)
(V5)
 (V6)
(V6)
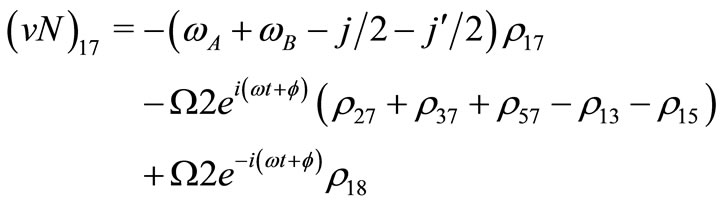 (V7)
(V7)
 (V8)
(V8)
 (V9)
(V9)
 (V10)
(V10)
 (V11)
(V11)
 (V12)
(V12)
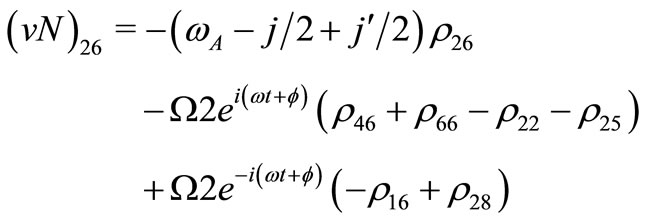 (V13)
(V13)
 (V14)
(V14)
 (V15)
(V15)
 (V16)
(V16)
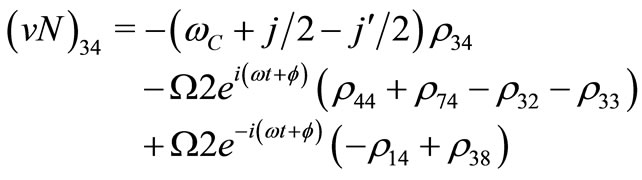 (V17)
(V17)
 (V18)
(V18)
 (V19)
(V19)
 (V20)
(V20)
 (V21)
(V21)
 (V22)
(V22)
 (V23)
(V23)
 (V24)
(V24)
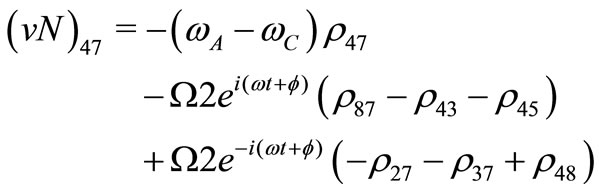 (V25)
(V25)
 (V26)
(V26)
 (V27)
(V27)
 (V28)
(V28)
 (V29)
(V29)
 (V30)
(V30)
 (V31)
(V31)
 (V32)
(V32)
 (V33)
(V33)
 (V34)
(V34)
 (V35)
(V35)
 (V36)
(V36)
Lindblad Part
Case A: Independent

 (A1)
(A1)
 (A2)
(A2)
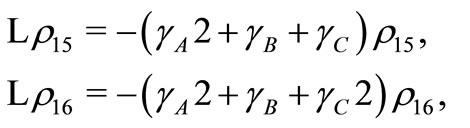 (A3)
(A3)
 (A4)
(A4)
 (A5)
(A5)
 (A6)
(A6)
 (A7)
(A7)
 (A8)
(A8)
 (A9)
(A9)
 (A10)
(A10)
 (A11)
(A11)
 (A12)
(A12)
 (A13)
(A13)
 (A14)
(A14)
 (A15)
(A15)
 (A16)
(A16)
 (A17)
(A17)
 (A18)
(A18)
 (A19)
(A19)
Case B: Pure Dephasing

 (B1)
(B1)
 (B5)
(B5)
 (B8)
(B8)
 (B13)
(B13)
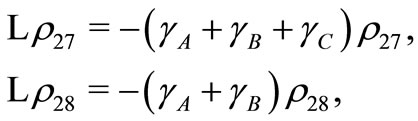 (B15)
(B15)
 (B19)
(B19)
 (B21)
(B21)
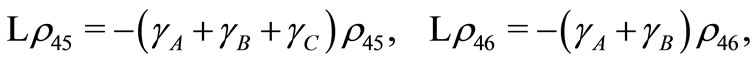 (B24)
(B24)
 (B26)
(B26)
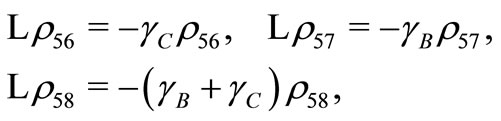 (B30)
(B30)
 (B33)
(B33)
 (B35)
(B35)
Case C: Independent Correlated
The Lindblad expression is given by

where  is as the case A, and it can be written as
is as the case A, and it can be written as
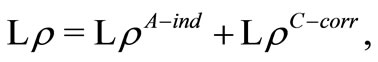
where the the independent part A corresponds to the case A above and the correlated part is

 (C1)
(C1)
 (C3)
(C3)
 (C5)
(C5)
 (C7)
(C7)
 (C9)
(C9)
 (C10)
(C10)
 (C11)
(C11)
 (C12)
(C12)
 (C13)
(C13)
 (C14)
(C14)
 (C15)
(C15)
 (C16)
(C16)
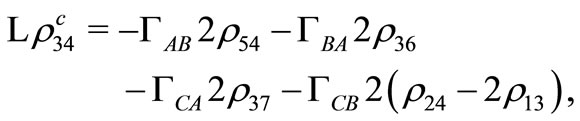 (C17)
(C17)
 (C18)
(C18)
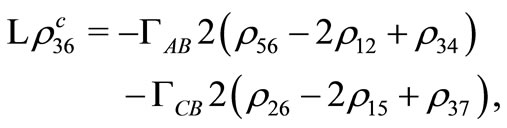 (C19)
(C19)
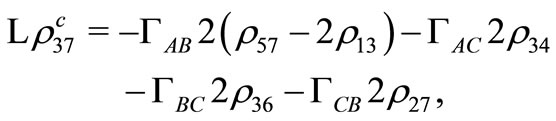 (C20)
(C20)
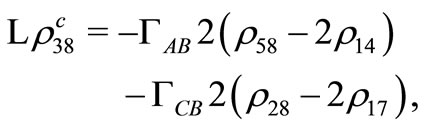 (C21)
(C21)
 (C22)
(C22)
 (C23)
(C23)
 (C24)
(C24)
 (C25)
(C25)
 (C26)
(C26)
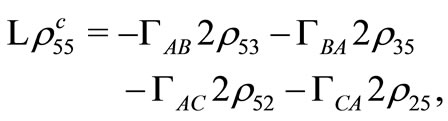 (C27)
(C27)
 (C28)
(C28)
 (C29)
(C29)
 (C30)
(C30)
 (C31)
(C31)
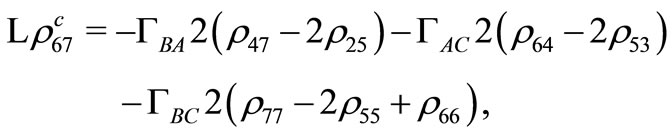 (C32)
(C32)
 (C33)
(C33)
 (C34)
(C34)
 (C35)
(C35)
 (C36)
(C36)
Case D: Dephasing Correlated
The Lindblad term is
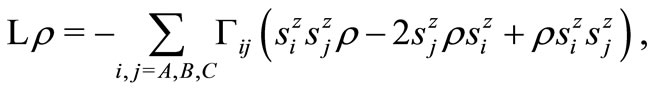
with  being the
being the  as the case B (Pure dephasing), and one has
as the case B (Pure dephasing), and one has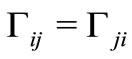 . This expression can be written as
. This expression can be written as

where 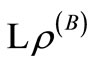 is the Lindblad term of the case B (pure dephasing), and the other term is given by
is the Lindblad term of the case B (pure dephasing), and the other term is given by

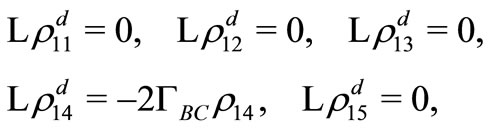 (D1)
(D1)
 (D2)
(D2)
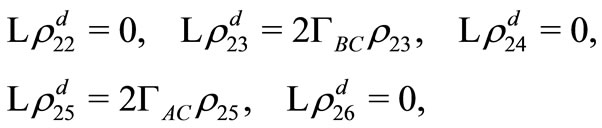 (D3)
(D3)
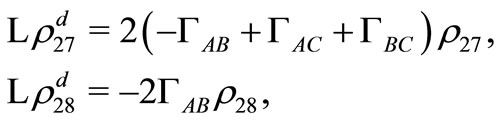 (D4)
(D4)
 (D5)
(D5)
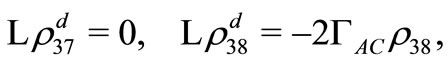 (D6)
(D6)
 (D7)
(D7)
 (D8)
(D8)
 (D9)
(D9)
 (D10)
(D10)
 (D11)
(D11)
 (D12)
(D12)