The Computation of Scalar Curvature in the Four-State Mixed Spin Model and the Investigation of Its Behavior: A Computational Study ()
1. Introduction
Displaying statistical-mechanics variables such as temperature and magnetic field as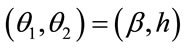 , the scalar-curvature function is computed through the below expression [1-15]:
, the scalar-curvature function is computed through the below expression [1-15]:
 (1)
(1)
where f is the reduced free energy on each site, and  [1-5]. The value of G is defined by the following equation [6-10]:
[1-5]. The value of G is defined by the following equation [6-10]:
 (2)
(2)
The only quantity defines a high-order transition near the critical point is the correlation length 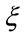 [11-15]. The scalar curvature according to
[11-15]. The scalar curvature according to  becomes dependent on this quantity in which d is the number of system’s dimensions [16-22]. If it is assumed that the super-scale equation
becomes dependent on this quantity in which d is the number of system’s dimensions [16-22]. If it is assumed that the super-scale equation 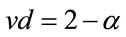 is true, we will have then [2-20]:
is true, we will have then [2-20]:
 (3)
(3)
A solvable model is considered to study the behavior of R. The one-dimensional Ising model possesses this feature. According to Equation (1), the scalar curvature obtained for this model is as follows [23-25]:
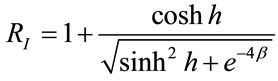 (4)
(4)
In this case,  is a positive value, and becomes divergent only at zero temperature and zero fields (critical point). The correlation length is given by the below equation:
is a positive value, and becomes divergent only at zero temperature and zero fields (critical point). The correlation length is given by the below equation:
 (5)
(5)
Near the critical point, we have ; and in comparison with Equation (3), it is in accordance with
; and in comparison with Equation (3), it is in accordance with 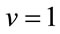 and
and  that is expected for these exponents.
that is expected for these exponents.
Through Equation (4), the scalar curvature for the onedimensional Potts model is calculated as below [23-25]:
 (6)
(6)
where , and
, and . In the above equation, the expressions A and B are as follows:
. In the above equation, the expressions A and B are as follows:
 (7)
(7)
In proportion to y and z, these expressions are functions with slow changes, and do not become divergent at the limited temperature and field (physical). The value of 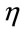 is computed by the below function:
is computed by the below function:
 (8)
(8)
In general, the expressions of ,
,  , and
, and  are very long for different values of q (however, they are easily achieved).
are very long for different values of q (however, they are easily achieved).
For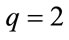 , Equation (6) is transformed into the following equation that is Equation (4) for the Ising model:
, Equation (6) is transformed into the following equation that is Equation (4) for the Ising model:
 (9)
(9)
In the zero fields , the expression R for the onedimensional Potts model is acquired as a much more compact form:
, the expression R for the onedimensional Potts model is acquired as a much more compact form:
 (10)
(10)
It is observed that through changing y from 1 to ∞, the value of R changes from  to ∞. Generally, the geometrical shape of R, that is a function of y and z, is the same. The correlation length for one-dimensional Potts model is defined as same as the correlation length for one-dimensional Ising model:
to ∞. Generally, the geometrical shape of R, that is a function of y and z, is the same. The correlation length for one-dimensional Potts model is defined as same as the correlation length for one-dimensional Ising model:
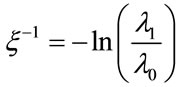 (11)
(11)
in which the eigenvalues of transfer matrix of one-dimensional Potts model is as follows:
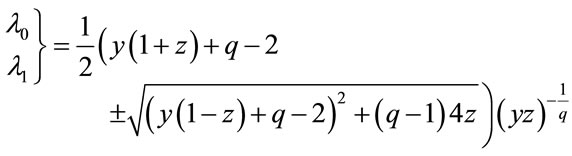 (12)
(12)
For  and
and , we have
, we have . Therefore, according to
. Therefore, according to  in
in , the anticipated scaled value of R for one-dimensional Potts model is obtained again. The exponents are also similar to the one-dimensional Ising model (
, the anticipated scaled value of R for one-dimensional Potts model is obtained again. The exponents are also similar to the one-dimensional Ising model ( ,
, ).
).
In Figure 1, the illustration of function R for Ising model ( ) is depicted. The symmetry
) is depicted. The symmetry  of Ising model with the transform of
of Ising model with the transform of  is evident in the graph of R.
is evident in the graph of R.
2. Analytical and Numerical Methods
The general Hamiltonian of this model is written as the below form [26-29]:
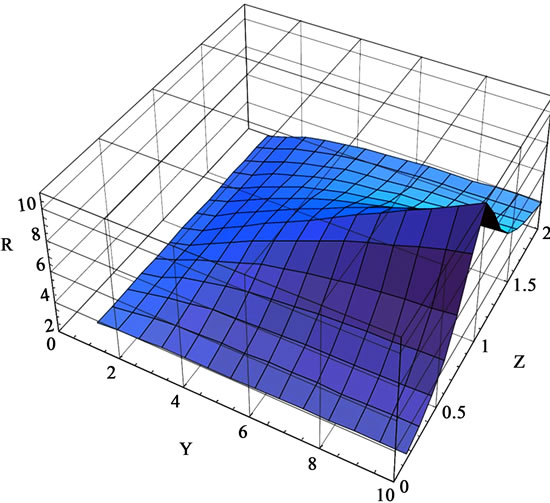
Figure 1. The scalar curvature for the one-dimensional Ising model. The maximum value of R is along the line z = 1.
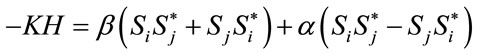 (13)
(13)
where ; α and β are two constants. The values of spins are as follows:
; α and β are two constants. The values of spins are as follows:
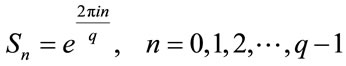 (14)
(14)
In other words, instead of  Ising, spins choose q states. The values of Ising spin are obtained in the particular state of
Ising, spins choose q states. The values of Ising spin are obtained in the particular state of . Based on the Perron-Frobenius theorem, the one-dimensional systems do not show phase transition. However, this model does not conform to this theorem on account of being mixed; despite being onedimensional, it has the first-order phase transition [26- 32]. The mixed model has various applications. Such actions in the lattice gauge theories are known as the Chern-Simons action, and effectively substituted for the fermions’ action in the gauge theories [33]. The mixed spin model causes the computations of the two-dimensional gravity and coupling of spins and random surfaces, and the determination of these models’ critical exponents as a solvable theory to improve [26-29]. In these states, first, a chain containing N spins with the periodic boundary condition of
. Based on the Perron-Frobenius theorem, the one-dimensional systems do not show phase transition. However, this model does not conform to this theorem on account of being mixed; despite being onedimensional, it has the first-order phase transition [26- 32]. The mixed model has various applications. Such actions in the lattice gauge theories are known as the Chern-Simons action, and effectively substituted for the fermions’ action in the gauge theories [33]. The mixed spin model causes the computations of the two-dimensional gravity and coupling of spins and random surfaces, and the determination of these models’ critical exponents as a solvable theory to improve [26-29]. In these states, first, a chain containing N spins with the periodic boundary condition of  is considered. The general partition function is written as the following form:
is considered. The general partition function is written as the following form:
 (15)
(15)
Through considering the nearest neighbors, we have:
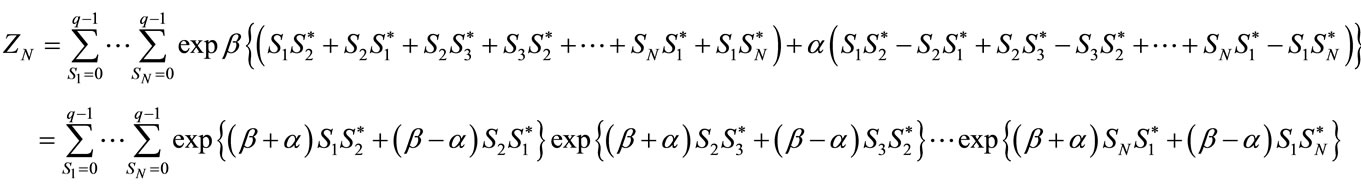 (16)
(16)
Now, each of the above terms can be considered as the transfer matrix’s elements:
 (17)
(17)
in which the general form of the transfer matrix’s elements is as follows:
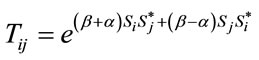 (18)
(18)
Since each of  s can have q values, the above matrix is a
s can have q values, the above matrix is a  matrix. As an example, this matrix for
matrix. As an example, this matrix for  is as follows:
is as follows:
 (19)
(19)
This matrix’s eigenvalues are as follows:
 (20)
(20)
Provided the above expressions’ maximum eigenvalue is determined, the reduced free energy on each site can be calculated. For this purpose, the problem is numerically solved. This can be conducted for a value of β, and to change the other parameter (α). Figures 2 and 3 demonstrate the mixed model’s phase transition for the constant values of β. Through studying these curves, and considering the absence of the first-order derivative in where the two peaks separate from the curve, the maximum eigenvalue can be computed. The absence of derivative in these peaks means the first-order phase transition. After the calculation of maximum eigenvalue, the scalar curvature is computed:

Figure 2. The curve of maximum eigenvalue for the onedimensional mixed lattice for β = 0.415 and q = 4.

Figure 3. The curve of maximum eigenvalue for the onedimensional mixed lattice for β = 0.43 and q = 4.
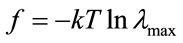 (21)
(21)
3. Results and Discussion
In this paper, the scalar curvature of one-dimensional mixed model for the particular case ( ) is calculated. The importance of this computation is that the scalarcurvature model is applicable not only to the systems with second-order phase transition but also to the systems with first-order phase transition. Hitherto, the systems with first-order phase transition have not been studied using the scalar-curvature model. For the first time, the possibility of applying this model to such problems is mooted in this work. In this regard, it is essential to determine the maximum eigenvalue among the four eigenvalues achieved in the previous section, and in proportion to the variables α and β. After this stage, the free energy is computed according to Equation (22) to determine the value of R. Then, through Equation (4), the scalar curvature is obtained for the four existing eigenvalues. The simplified values of scalar curvature for the four mentioned eigenvalues are as follows:
) is calculated. The importance of this computation is that the scalarcurvature model is applicable not only to the systems with second-order phase transition but also to the systems with first-order phase transition. Hitherto, the systems with first-order phase transition have not been studied using the scalar-curvature model. For the first time, the possibility of applying this model to such problems is mooted in this work. In this regard, it is essential to determine the maximum eigenvalue among the four eigenvalues achieved in the previous section, and in proportion to the variables α and β. After this stage, the free energy is computed according to Equation (22) to determine the value of R. Then, through Equation (4), the scalar curvature is obtained for the four existing eigenvalues. The simplified values of scalar curvature for the four mentioned eigenvalues are as follows:
 (22)
(22)
The scalar curvature for the maximum eigenvalue of transfer matrix is selected among the above four values. This means that changing the values of α and β, the maximum eigenvalue is substituted among the four existing eigenvalues, since the functions constituting these eigenvalues are trigonometric functions. In Figure 4, the three-dimensional graph of maximum eigenvalue is illustrated. On this surface, points’ derived curve is discontinuous for a value of β and along a line of variable α are the system’s transition points being in the surface’s depth in the figure. Figures 5 and 6 indicate the curve of changes in R for different values of β. Through investigating these curves, it can be observed that the value of R becomes divergent (the same as Ising and Potts models) in the points the derived curve has discontinuity (critical point).

Figure 4. The maximum eigenvalue according to the different values of α and β in the one-dimensional mixed spin model and for q = 4.

Figure 5. The curve of scalar curvature for the one-dimensional mixed lattice for β = 0.415 and q = 4.
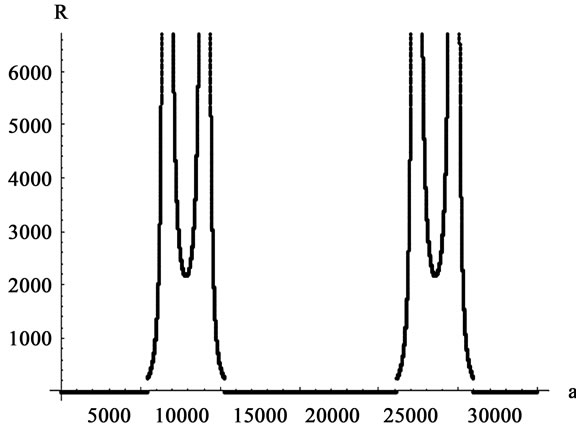
Figure 6. The curve of scalar curvature for the one-dimensional mixed lattice for β = 0.43 and q = 4.
Generally, analytically computing the mixed model’s scalar curvature for every desirable q is difficult in mathematical terms. The numerical methods can be employed to calculate this quantity for every value of q. This can be performed after calculating eigenvalues and free energy’s derivatives in proportion to β and h. Finally, the scalar curvature of R is computed using Equation (1). An interesting event occurs in the computation of R for the three-state model. In this special case, the transfer matrix’s eigenvalues are obtained as follows:
 (23)
(23)
Through utilizing these values, and calculating the value of R for each of them, it can be concluded that all the three values of R are equal ( ). The reason why these three values are equal and the phase transition is not shown still remains unknown to us. In this regard, this matter can be studied as another problem.
). The reason why these three values are equal and the phase transition is not shown still remains unknown to us. In this regard, this matter can be studied as another problem.
4. Conclusion
In this paper, through the scalar-curvature model, the fourstate one-dimensional mixed model with the first-order phase transition is investigated. The computed scalar curvature becomes divergent at the points this system has phase transition. This result is consistent with the expected quantity and how it behaves for the other models with the second-order phase transition (the same as three-state Ising and Potts models). The present paper’s results indicate that the scalar-curvature model can have an important role to play in the investigation of all the statistical systems with the phase transition of every order; in other words, it is a new mathematical approach toward such problems. However, the Riemannian Bures metric on the space of (normalized) complex positive matrices is used for parameter estimation of mixed quantum states based on repeated measurements just as the Fisher information in classical statistics. It appears also in the concept of purifications of mixed states in quantum physics. Therefore, and also for mathematical reasons, it is natural to ask for curvature properties of this Riemannian metric. Here we determine its scalar curvature and Ricci tensor and prove a lower bound for the curvature on the submanifold of trace-1 matrices. This bound is achieved for the maximally mixed state, a further hint for the statistical meaning of the scalar curvature.
5. Acknowledgements
The work described in this paper was fully supported by grants from the Institute for Advanced Studies of Iran. The authors would like to express genuinely and sincerely thanks and appreciated and their gratitude to Institute for Advanced Studies of Iran.
NOTES