Hybrid Amplification: An Efficient Scheme for Energy Saving in MIMO Systems ()
1. Introduction
Multiple Input Multiple Output (MIMO) systems are a very promising technique for achieving high capacity in wireless communication links [1,2]. Among these systems, Vertical Bell Labs Layered Space-Time (VBLAST) technology is very popular thanks to its simplicity and to the performances that have been attained (20 - 40 b/s/Hz [3]). Moreover, it has recently be shown that one way for obtaining higher spectral efficiencies for these systems consists in adapting transmission parameters such as modulation rate as well as RF power for each transmit antenna. In [4], a transmit RF power allocation scheme is given in order to minimize the Bit Error Rate (BER) considering a total transmit RF power constraint. In [5], the authors propose an efficient solution for power and rate control in an extended VBLAST system using MQAM modulations. The impact of imperfect channel estimation on adaptive VBLAST performances is estimated in [6,7]. A different approach is foreseen in [8,9] where power and rate adaptation are used for improving protocol performances (Go-Back-N and TCP). The work presented in [10] combines transmit antenna selection with rate and power control for VBLAST systems in correlated channels, significant improvement is obtained on BER performance. An iterative bit and power allocation algorithm has also been presented in [11], for Orthogonal Frequency Division Multiplexing (OFDM) VBLAST systems, for minimizing the total RF power while maintaining a reliable communication system.
In the work presented here, we add a realistic amplification model to adaptive VBLAST system simulations. This model is then used to present an efficient scheme for saving energy in MIMO systems. The amplification model we use brings two important modifications in comparison to previous works:
First, algorithms that have been used in the papers previously presented (we name them “classical” algorithms in the following), often consider the minimization of the total transmit RF power as the optimization parameter. Now, unless multi-user systems are studied (then interferences between users must be minimized and then total RF power must also be minimized), it is the total DC-power consumption of the system that is important to minimize. As the DC-power consumption of an amplifier is similar to a second-degree function of the RF power, the optimization theoretical study becomes much more complex. In this paper, we take the exact form of the amplifier DC-power consumption into account and add it in the system simulations.
Besides, classical algorithms don’t take into account the different behavior of the transmit amplifier for each constellation. Indeed, each constellation has a different peak-to-average and thus requires a different back-off in front of the amplifier. Thus, the maximum RF power that can be attained on an amplifier depends on the kind of modulation that is currently used (as well as filtering and coding). In this work, we consider the exact back-off required for each constellation with realistic amplifier models We use this realistic amplification model for adaptive VBLAST systems in order to show that a degree of freedom is currently not used in MIMO systems for decreasing energy consumption. Indeed, telecommunications links are designed to respond to the worst channel conditions. For some important part of the total communication time, the link conditions are better than the worst case. Now, in a MIMO system, several transmit RF chains are available. If all the transmit amplifiers have the same consumption behaviors (what we name “homogeneous scheme”), the adaptation algorithm that chooses which transmitter must transmit which part of the data, has no choice for minimizing the consumption (The Automatic Gain Control is not an optimal solution as the DC-RF conversion efficiency drops when the RF power is decreased). On the other hand, if amplifiers with different consumption behaviors are used, a clever algorithm can decrease the system energy consumption. In the following work, we show that distributing, in an optimal way, different amplifiers with different powers in a MIMO system is a very efficient scheme for saving energy.
The outline of this contribution is as follows. Section 2 provides an overview of the VBLAST system used for the simulations, a realistic form (taking into account the amplifier model) for the computing of the Signal-toNoise ratio is proposed. Section 3 describes the realistic amplification model that is implemented for the simulations; numerous results concerning DC-power consumption as well as maximal RF power are presented for different MQAM constellations. Section 4 discusses the major concept of this paper, i.e. MIMO system hybrid amplification (where different kinds of amplifiers are used), the adaptive algorithm that is used is summed up and the effect of this kind of amplification on the system performances is discussed. The impact of the detection order (of the different transmit symbols) is also highlighted. Then, simulation results concerning the behavior of hybrid or homogeneous amplification schemes are provided in Section 5. Several peak-power distributions for the amplifiers as well as different detection orders are tested. The possible energy savings with hybrid amplification are clearly highlighted. Finally, concluding remarks are presented in Section 6.
2. System Overview
2.1. System Model
We consider an Nt × Nr MIMO system with Nt transmit antennas and Nr receive antennas (Nr ≥ Nt) shown on Figure 1. This system is designed to ensure constant capacity when a given minimal SNR is present on the receive antennas. This kind of system is present in a lot of real-time transmission systems such as video streaming, etc. Moreover, the hardware design complexity can be significantly reduced if the total information throughput remains constant [10].
The received signal vector y can be expressed as a function of the transmit signal vector x, the Nt × Nr channel matrix H, the Nt × Nt power matrix P and the Nr-dimensional noise vector n (of variance σ2) by (1).
 (1)
(1)

Figure 1. Adaptive VBLAST system overview.
The elements hij of H are assumed to be uncorrelated and identically distributed complex Gaussian random variables with zero mean and unit variance (Rayleigh fading) [2]. P is a diagonal matrix whose elements are the square roots of the different amplifier RF powers ( ).
).
The transmission is organized into bursts of L independent symbols. The channel is assumed to be constant during one transmission burst and may vary between bursts. For each burst, a BPSK mapped pilot is used for channel estimation and for determining the rate and power for each antenna. The impact of the form and length of this pilot are not studied in this paper. Thus, the capacity loss due to this pilot is not taken into account in the following results. It is assumed that the channel is perfectly estimated. The receiver chooses the constellation as well as its RF power for each antenna thanks to the MIMO sub-channel Signal-to-Noise Ratio (SNR) and sends this information through an error-free feedback channel.
The VBLAST Zero-Forcing Successive Interference Cancellation (ZF-SIC) detection algorithm that is implemented is described in details in [3]. Depending on the detection order that is chosen, one of the transmit symbols is detected thanks to linear nulling of the other symbols, then its contribution to the received signal vector is evaluated and subtracted to this signal. This process is repeated until all Nt symbols are detected. The postdetection SINR (Signal-to-Interference and Noise Ratio), γk, for the kth-detected component of the transmitted vector is given by (2):
 (2)
(2)
where the numerator represents the mean RF power of the used constellation, σ2 is the noise variance and wk is the kth line of Moore-Penrose pseudo-inverse of the channel matrix H [3]. These SINRs are computed for evaluating the rate and power that can be used for each transmit antenna.
Indeed, it has been shown that, for SISO (Single Input Single Output) systems with a SNR γ, the upper bound of the Bit Error Rate (BER) is given by (3) for a MQAM (M ≥ 4) constellation and by (4) for a BPSK constellation [12].
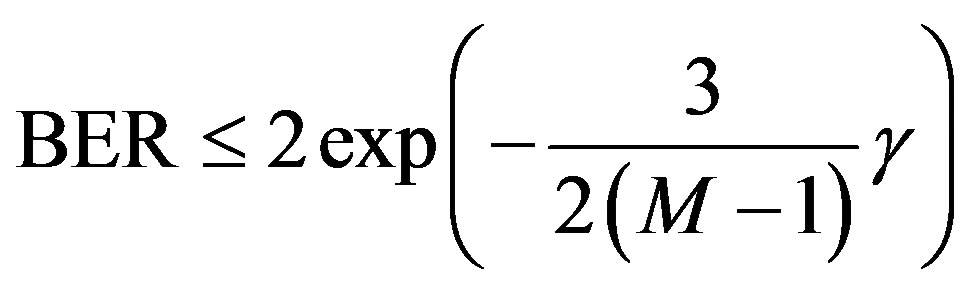 (3)
(3)
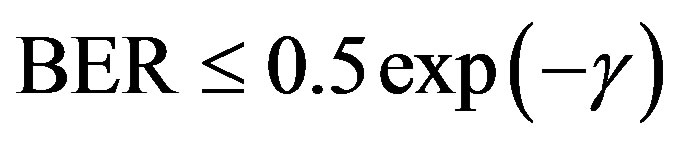 (4)
(4)
Thus, for a target BER, it is possible to determine the minimal SNR that is needed for the use of a constellation. It is important to note that the MIMO system BER that will be obtained can be slightly higher than the prediction of (3) and (4). Indeed, the error propagation due to a false symbol in an early stage of the detection algorithm is not taken into account by these equations. Nevertheless, the bounds (3) and (4) are quite pessimistic for SNRs between 0 and 30 dB [13] and eventually tighter bounds could be defined by simulation. For simplification, we use the bounds (3) and (4) in this work.
2.2. Realistic Signal-to-Noise Ratio
In classical adaptive algorithms, the SINRs γk that are calculated are independent of the amplification stage behavior. In real systems, the power amplifier of a transmitter is used for all possible constellations. In such a case, fixing the same RF power for all constellations means operating at the power level imposed by the highest back-off. Such mode of operation is clearly not the most efficient. Variable back-offs must, therefore, be considered for more accurate system modeling. These back-offs depend on the constellation, the amplifier’s operation class as well as the predistortion, if any, that is used (the predistortion increases the back-off required). The kind of filtering and coding also have an influence on these back-offs.
Thus, new post-detection SINRs γ′ taking into account the variation of the RF power when the constellation is changed must now be considered (5).
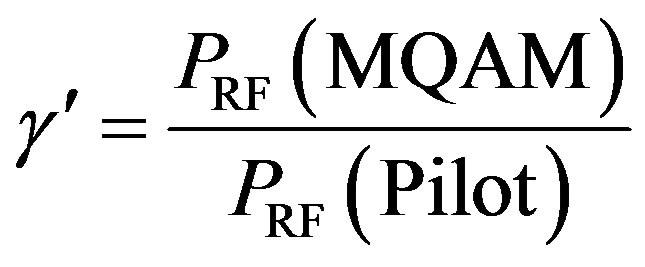 (5)
(5)
where PRF (MQAM) is the RF power of the MQAM constellation that is tested for its eventual use, PRF (Pilot) is the RF power of the pilot constellation and γpilot is the post-detection SINR obtained with the pilot constellation.
The RF power required for a given constellation can be obtained by simulation using realistic models of the amplifier and predistortion method as detailed in the following section.
3. Realistic Amplification Model
3.1. Amplifier Model
The model that is used for the Nt amplifiers at the transmitter is based on measured data of a 45-Watts peak Motorola MRF21045 base station amplifier [14]. This amplifier is biased in class AB and its characteristics in terms of DC-RF conversion efficiency and power gain are given in Figure 2.
3.2. Predistortion
The gain of the amplifier is kept to a constant value of 13.25 dB over an input power range of –10 dBm to 34.1

Figure 2. Gain and DC-RF conversion efficiency of the MRF- 21045 amplifier.
dBm thanks to a baseband predistortion technique. Each input power value is predistorted in order to produce the output power corresponding to a constant gain. This operation is done with the AM/AM predistortion curve shown on Figure 3.
3.3. Results
For each constellation, preliminary simulations have been carried out for determining the maximum RF powers that can be attained on the predistorted MRF21045 amplifiers. This is done in such a way that less than 0.1% of the input signal (20000 symbols) is beyond the predistortion limit (34.1 dBm) and thus is peak-limited. Results are given in Table 1 for MQAM signals filtered with a Raised Cosine Filter (RCF) of varying roll-off factor. No data coding is assumed. It is important to note that these powers are lower than those obtained without predictortion. Indeed, predistortion increases the crest factor of the signal input to the amplifier thus requiring a greater

Figure 3. Gain and AM/AM predistortion curve for the MRF21045 amplifier.

Table 1. Maximal RF powers (W) for different constellation sizes.
back-off relative to the original signal. Moreover, it can be seen that the impact of the filtering roll-off factor on the RF power varies from constellation to constellation. Indeed, the distribution of the symbols in each constellation influences both the peak-to-average of the filtered signal and the predistortion function impact on the required back-off.
The mean DC-power consumption has also been evaluated for each constellation with these RF powers. The results are given in Table 2.
Tables 1 and 2 represent the maximal RF power that can be used for each constellation and its respective DCpower consumption for this kind of amplifier. As an Automatic Gain Control (AGC) is implemented in our VBLAST system, the same work has been done for lower RF powers. Thus, for each constellation, the DCpower consumption has been computed for each RF power decrease (by 1 dB step) until a drop of 15 dB of this power. All these data will be available for the adaptive algorithm presented in the following section.
4. Hybrid Amplification
4.1. Concept
As we said in the introduction of this paper, a wireless communication link is calculated for the worst channel conditions. During an important part of the transmission time, channel conditions are better (the SNR is higher). In this case, if the different transmitter RF chains have different DC-power consumption behaviors, the adaptive algorithm can adjust their rates and powers to minimize the energy consumption while keeping the target performances.
Thus, in the hybrid amplification scheme we propose, the different power amplifiers of the MIMO system have different peak powers. For example, in a 4 × 4 MIMO system, PA1 and PA3 have 47 dBm peak-power, PA2 and PA4 have 41 dBm peak-power (Figure 4). Other

Table 2. Mean DC-power consumption (W) for different constellation sizes.

Figure 4. MIMO Hybrid amplification example.
schemes can comport three different peak-powers and so on. In this way, the amplifiers have different behaviors concerning the RF power they can deliver and the DCpower they use. The power differences between amplifiers, the number of amplifiers for each power, eventually the space distribution of the RF chains (when correlated channel are assumed) constitute the different parameters to optimize.
For what concerns the first study presented in this paper, we consider that the amplifier behavior in terms of DC-RF efficiency and gain are only translated when the peak-power is changed. Thus, if with a 47 dBm peakpower model, BPSK can be transmitted with 8.6-W RFpower and a DC-power consumption of 49.5 W (Tables 1 and 2), then, with a 41 dBm peak power model, BPSK will be transmitted with  = 2.15 W RF power and 12.4 W DC-power consumption. Certainly, technology differences can affect these results but we think that the proposed behavior is a quite good model for this first study.
= 2.15 W RF power and 12.4 W DC-power consumption. Certainly, technology differences can affect these results but we think that the proposed behavior is a quite good model for this first study.
Besides, it must be added that these different peak powers can be obtained with different kind of amplifiers but also with the same amplifiers bias-polarized in different ways. These technological aspects will be investigated in a further work.
4.2. Adaptive Algorithm
In this section, we present a short summary of the adaptive algorithm used for the system simulations. This greedy-based algorithm takes into account the DC-power consumption behavior of each transmitter to save energy.
1st recursion:
Test all transmitter SINRs to decide where the rate can be increased with respect to the target BER (by 1 or 2 bits steps).
Among transmitters whose rate can be increased, choose the transmitter whose ΔPdc is minimal (i.e. the difference between the DC-power consumption of the previous an the new constellation).
Repeat the above recursion while system capacity < target capacity.
2nd recursion (AGC):
Considering each transmitter rate and power, calculate the foreseeable BER.
If the foreseeable BER < target BER, decrease the RF power by ΔPrf.
Repeat the above recursion while the foreseeable BER < target BER for each transmitter.
4.3. System Performances and Mean SINR with Both Amplification Schemes
As it can be seen in (2), the equivalent SINR at each detection step depends on the RF power of the used constellation, the norm of the kth line of the channel matrix pseudo-inverse and the noise variance σ2. In comparison to the homogeneous amplification scheme, the SINR of the low power transmitter is lower and that of the high power transmitter is higher. Nevertheless, the mean SINR of the hybrid amplification system is different than its equivalent with homogeneous amplification even if the same total RF power is present. Indeed, the Moore-Penrose pseudo-inverse of a matrix is a non-linear process. Moreover, this mean SINR differs in function of the detection order that is chosen (see next part).
Nevertheless, the mean SINR doesn’t represent the system performances in a precise way. Indeed, that is the SINR, present for each symbol, which is important. Thus, theoretically, in an uncorrelated MIMO channel, the total capacity would be given by (6) [15].
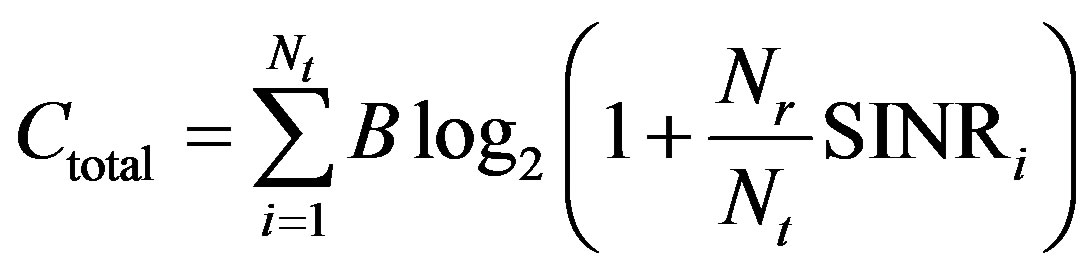 (6)
(6)
where B is the channel bandwidth.
For one MIMO sub-channel, the mean difference between the capacity of the hybrid scheme and that of the homogeneous scheme will be given by (7).
 (7)
(7)
where ΔP is the RF power difference between the amplifiers in the hybrid configuration.
Figure 5 shows the relative capacity difference ΔC for Nt = Nr, B = 1 and different values of ΔP. It can be seen that for high SINRs and low ΔP, the difference is negligible. Nevertheless, when the SINR decreases and for important values of ΔP, this difference becomes significant. It is this behavior, which limits the maximum ΔP acceptable for the system.
In the following, for comparing the two amplification schemes, we rely on capacity, BER and power consumption performances. We will see that real system simulations validate the capacity behavior given by (7). Thus, an optimal choice of the power difference must be done for saving some energy while keeping the same system performances.

Figure 5. Relative difference of sub-channel capacities for hybrid and homogeneous amplification schemes.
4.4. Symbol Detection Order
Different studies have been done to find the best detection order of the different transmit symbols in VBLAST algorithms. For non-adaptive algorithms (when the constellations are identical for all transmitters), the symbol with the higher SINR must be decoded in first place (forward detection order) [3]. For adaptive algorithms, it is explained in [5] that the ordering has no impact on the capacity attained by the system. In [16], it is shown that a reverse detection order (i.e. the symbol with the lower SINR in first place) is best suited to this kind of systems. Moreover, fixing a constant detection order can be desirable because it avoids computing several channel matrix inversions (for optimal order search) [10].
When hybrid amplification is assumed, a fixed and efficient detection algorithm can be used. Indeed, the more numerous symbols have been detected, the more the post-detection SINR increase. Thus, one way to use, more often, low consumption amplifiers is to detect symbols transmitted by these RF chains in last place. In this way, their SINRs are increased and more bits can be affected to them. The DC-power consumption is thus decreased in comparison to other detection orders. Simulation results will describe this behavior in the following section. Nevertheless, we will see that the direct detection order is quite better concerning BER performances.
5. Simulations
Simulations using the homogeneous amplification (same amplifiers for all transmitters) as well as the hybrid amplification (different amplifiers with different peak powers distributed in different ways on the transmitters) have been carried out for a Nt × Nr VBLAST system. The adaptation and detection algorithms previously presented in Sections 2 and 4 as well as the realistic amplification model presented in Section 3 have been implemented.
The influence of different system parameters, such as the number of antennas, the filtering roll-off factor, the choice of MQAM constellations as well as the target BER, have been studied in [17] for the homogeneous amplification scheme.
The simulations are conducted for 100000 symbols. The channel is constant over one burst, i.e. 100 symbols, and varies from burst to burst (i.e. 1000 uncorrelated channels are tested for each simulation). The default configuration consists of a 4 × 4 system with data filtering using a RCF with 0.5 roll-off factor. The target capacity is 8 b/s (i.e. 6.3 b/s/Hz for the 0.5-RCF considered here), the target BER is 10–3 and the different available constellations are: BPSK, QPSK, 16QAM, 64QAM, 256QAM. The detection order that is used is a forward ordering (different possible detection orders are studied in details in Section 5.2). The SNR, shown on the x-axis for some simulation results, corresponds to the receive antenna SNR, it is higher than the mean post-detection SINR in the VBLAST algorithm. The minimal SNR (i.e. the worst channel condition) for ensuring the target capacity is 23 dB (this value has been obtained by simulation). Under this limit, we assume that the transmission is interrupted. Data of Tables 1 and 2 are used for the different MQAM constellations.
5.1. Hybrid Amplification with 4.8 dB Peak-Power Difference between Amplifiers
In this section, we compare two 4 × 4 MIMO systems. The first system is constructed with an hybrid amplification scheme. The peak powers of the different amplifiers are the followings: {P1 = Pref, P2 = Pref – 4.8 dB, P3 = Pref, P4 = Pref – 4.8 dB}. The second amplification scheme is homogeneous; the RF powers are calculated such that the total transmit RF power is the same than in the first scheme.
Thus, P1 = P2 = P3 = P4 = . In our simulations, Pref is set to 47 dBm, as it is the original peak power (considering the predistortion) of the MRF- 21045 model, but it could be any other value calculated in function of the telecommunications link.
. In our simulations, Pref is set to 47 dBm, as it is the original peak power (considering the predistortion) of the MRF- 21045 model, but it could be any other value calculated in function of the telecommunications link.
Figure 6 shows the performance results in terms of capacity and BER for both amplification schemes. We can see that above the minimal SNR (23 dB), both systems attain the target capacity.
Concerning the BERs, there are slight differences due to the different use of the amplifiers (presented in Figures 7 and 8). Indeed, below 23 dB, the hybrid configuration uses less transmitters (the two high power amplifiers are mainly used) than the homogeneous scheme. Thus, higher order constellations are more often used and as their symbol error probably is higher, the total BER is slightly higher. Above 23 dB, the inverse situation takes place. The homogeneous configuration uses less trans-

Figure 6. Performance results for both amplification schemes.

Figure 7. Amplifiers use vs SNR for hybrid amplification scheme.

Figure 8. Amplifiers use vs SNR for homogeneous amplification scheme.
mitters (their amplifiers have more power than the low power amplifiers of the hybrid configuration), thus, higher order constellations are more often used and the total BER is slightly higher. Under the 23 dB limit, the target capacity is not attained by both systems; thus, no transmission will be allowed (in the real-time system that we consider).
Figures 7 and 8 represent the use of the different amplifiers for the total SNR range and both amplification schemes. Above 20 dB, one can see that the low power amplifiers are much more used thanks to the adaptive algorithm of the hybrid scheme presented in Section 4.2. Each time that the algorithm has choice, it chooses the amplifier with the lower power. Under 20 dB, the algorithm must use high power amplifiers for increasing the capacity in order to attain the target capacity. Of course, this limit depends on the target capacity and BER.
5.2. Impact of Detection Order for Both Amplification Schemes
Figures 9 and 10 show results concerning the VBLAST

Figure 9. Impact of detection order on system capacity for hybrid scheme.

Figure 10. Impact of detection order on system energy consumption for hybrid scheme.
system performances as well as its power consumption for different detection orders. The hybrid amplification scheme is used with ΔP = 4.8 dB. Four detection orders are tested: forward, reverse (see Section 4.4), fixed to (Tx3, Tx1, Tx4, Tx2), named fixed forward, and fixed to (Tx4, Tx2, Tx3, Tx1), named fixed reverse. In the fixed forward order, the two low power amplifier transmitters are always decoded in last place while in the fixed reverse order, they are always decoded in first place. The second low amplifier transmitter (Tx4) is decoded before the first one (Tx2) because of the adaptive algorithm. Indeed, more bits are allowed (in the average) to Tx2 than to Tx4 and to Tx1 than to Tx3 (simply because they are tested in first place for the rate allocation).
Concerning the capacity (Figure 9), the reverse orders (fixed and variable) are better than the forward orders at low SNRs. Indeed, with these algorithms, one increases the SINRs of the good sub-channels (those which are already high) by decoding them in last place. Thus, bits can be transmitted on these sub-channels. Nevertheless, the different capacities converge to 8 b/s at 23 dB and the differences for this SNR are negligible.
Concerning the power consumption (Figure 10), forward detection orders are outperformed by reverse ones under 23 dB but above this limit, they are better. Indeed, in these algorithms, as one increases the SINRs of the low power amplifier transmitter, one can use them more often than in the reverse algorithms.
The choice between the fixed and optimal forward orders depends on the system performances that we want to privilege: power consumption or speed of the receiver algorithm.
Finally, we don’t study in details the BER performances of each algorithm here but it can be added that above 23 dB, the forward orders are also better than the reverse orders for what concerns the BER (for a constant target capacity).
5.3. Impact of Power Difference between Amplifiers
As it has been explained in Section 4.3, we must choose the optimal power difference between amplifiers to keep optimal system performances while saving the maximal energy. In this section, we study the exact impact of the power difference between the amplifiers (used in the hybrid scheme) on the system performances as well as on the global energy saving.
We have simulated a 4 × 4 MIMO system with different kinds of amplification. For all simulations, the conditions are identical (same MIMO channels, same transmitted bits). The difference between amplifiers ΔP varies between 0 dB (i.e. the homogeneous scheme) and 7.8 dB. The peak powers of the different amplifiers for the hybrid amplification are the followings: {P1 = Pref, P2 = Pref – ΔP, P3 = Pref, P4 = Pref – ΔP}. The second amplification scheme is homogeneous, all the amplifiers are identical and P1 = P2 = P3 = P4 = .
.
The results concerning system performances as well as energy savings are presented on Figures 11 and 12 for each SNR value and for different power differences.
Figure 11 shows the relative difference between capacities for the different hybrid schemes in comparison to the homogeneous scheme. First, we can note that the form of these results agree well with the theoretical predictions discussed in Section 4.3 (Figure 5). Moreover, if we consider the 23-dB limit for the functioning of our telecommunication link, results show that above ΔP = 5 dB, the target capacity is not attained. Thus, even if energy savings quickly increase with the power difference ΔP (Figure 12), we must limit the power difference to 4.8 dB for this system. Of course, if different target capacities or minimal SNRs would be considered, then