The R-W Metric Has No Constant Curvature When Scalar Factor R(t) Changes with Time ()
The true meaning of the constant  in the Robertson-Walker metric is discussed when the scalar factor
in the Robertson-Walker metric is discussed when the scalar factor  changes with time. By strict calculation based on the Riemannian geometry, it is proved that the spatial curvature of the R-W metric is
changes with time. By strict calculation based on the Riemannian geometry, it is proved that the spatial curvature of the R-W metric is . The result indicates that the R-W metric has no constant curvature when
. The result indicates that the R-W metric has no constant curvature when 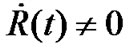 and
and 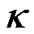 is not spatial curvature factor. We can only consider
is not spatial curvature factor. We can only consider  as an adjustable parameter with
as an adjustable parameter with  in general situations. The result is completely different from the current understanding which is based on the precondition that the scalar factor
in general situations. The result is completely different from the current understanding which is based on the precondition that the scalar factor  is fixed. Due to this result, many conclusions in the current cosmology such as the densities of dark material and dark energy should be re-estimated. In this way, we may overcome the current puzzling situation of cosmology thoroughly.
is fixed. Due to this result, many conclusions in the current cosmology such as the densities of dark material and dark energy should be re-estimated. In this way, we may overcome the current puzzling situation of cosmology thoroughly.
1. The R-W Metric Has No Constant Curvature When Scalar Factor  Is Related to Time
Is Related to Time
Standard cosmology takes the Robertson-Walker metric as the basic framework of space-time. According to the principle of cosmology, our universe is uniform and isotropic. It is proved that the space with homogeneity and isotropy is the one with constant curvature [1]. The R-W metric which is considered to be the one with maximum symmetry is
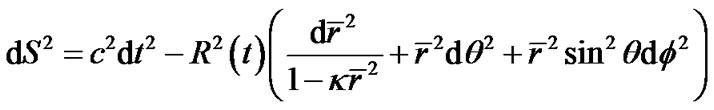 (1)
(1)
According to the current understanding, the constant  in (1) is considered to be a spatial curvature factor. That is to say, the R-W metric is with constant curvatures. When space is flat, we have
in (1) is considered to be a spatial curvature factor. That is to say, the R-W metric is with constant curvatures. When space is flat, we have 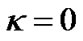 and the metric becomes
and the metric becomes
 (2)
(2)
According to the current understanding, the term of three dimensional spaces in bracket in (2) is flat. By multiplying a scalar factor  which does not depend on spatial coordinates, the spatial term can still be considered as flat. However, this turned out to be not true. We will prove below that when
which does not depend on spatial coordinates, the spatial term can still be considered as flat. However, this turned out to be not true. We will prove below that when , the R-W metric has no constant spatial curvature. The spatial curvature is related to
, the R-W metric has no constant spatial curvature. The spatial curvature is related to , although it still does not depend on spatial coordinates.
, although it still does not depend on spatial coordinates.
To explain this result clearly, let’s first repeat the deduction procedure of the R-W metric. As we know in geometry that the lower dimensional curved space can be embedded in the higher dimensional flat space. The three dimensional space with a constant curvature  can be considered as a super-curved surface embedded in the four dimensional flat space. The flat space-time metric of four dimensions can be written as
can be considered as a super-curved surface embedded in the four dimensional flat space. The flat space-time metric of four dimensions can be written as
 (3)
(3)
The condition of three dimensional super spherical surface in the four dimensional space-time is
 (4)
(4)
Here  is the radius of super-spherical surface and constant
is the radius of super-spherical surface and constant  is the curvature of super-spherical surface. From the formula above, we get
is the curvature of super-spherical surface. From the formula above, we get
 (5)
(5)
Substituting (5) in (3) and introducing coordinate transformation ,
,  , and
, and , we get three dimensional super-curved surface metric with a constant curvature
, we get three dimensional super-curved surface metric with a constant curvature 
 (6)
(6)
When co-moving coordinate  is used and time is fixed with
is used and time is fixed with  and
and  constant, (6) can be written as
constant, (6) can be written as
 (7)
(7)
Here  is considered as new space curvature. When time is not fixed and
is considered as new space curvature. When time is not fixed and  constant, according the current understanding, we can let
constant, according the current understanding, we can let  and extend (7) into
and extend (7) into
 (8)
(8)
On the other hand, the metric of four dimensional space-time in which the three dimensional space has a constant  is
is
 (9)
(9)
We think that it possible to introduce united cosmic time in the expanding universe with homogeneity and isotropy. So at last, the four dimensional metric of spacetime can be written as
 (10)
(10)
This is the standard procedure to derive the R-W metric. It is obvious that the deduction is not strict. We only prove that the metric (6) has a constant curvature . When
. When  constant, we have not proved that the metrics (8) and (9) still have constant curvatures. In fact, when
constant, we have not proved that the metrics (8) and (9) still have constant curvatures. In fact, when  constant, by using
constant, by using  in (6), we get
in (6), we get
 (11)
(11)
Similarly, substituting  in (9), we get
in (9), we get
 (12)
(12)
We can not get (8) and (10) from Equations (6) and (9). That is to say, when  or
or  constant, we have not proved that the constant
constant, we have not proved that the constant  is still the spatial curvature factor of the R-W metric!
is still the spatial curvature factor of the R-W metric!
However,  is generally considered as the curvature constant of the R-W metric and the spatial part of the metric is considered being flat when
is generally considered as the curvature constant of the R-W metric and the spatial part of the metric is considered being flat when  at present. This is because that the spatial part of three dimension metric in the bracket of (2) is flat. When it multiplies a scalar factor which does not depend on spatial coordinates, the space can be still considered flat. On the other hand, when
at present. This is because that the spatial part of three dimension metric in the bracket of (2) is flat. When it multiplies a scalar factor which does not depend on spatial coordinates, the space can be still considered flat. On the other hand, when 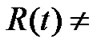 constant, we have metric tensor
constant, we have metric tensor  constant, (2) is obviously not the metric of flat space. In fact, the metric of the four dimensional flat space-time is
constant, (2) is obviously not the metric of flat space. In fact, the metric of the four dimensional flat space-time is
 (13)
(13)
By using co-moving coordinate , we get
, we get
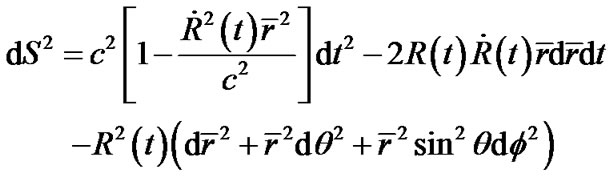 (14)
(14)
This form is completely different from the R-W metric (2) when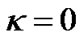 . The space-time of metric (14) seems to be curved, but it is flat essentially. According to the principle of the Riemannian geometry, if we can find a transformation to turn a curved space into flat, then the original space is flat essentially. If we can not find such a transformation, the original space is a really curved space. Now, because we can find a transformation to turn (14) into (13), the metric (14) is flat essentially. Because we can not find a transformation to turn (2) into (13) when
. The space-time of metric (14) seems to be curved, but it is flat essentially. According to the principle of the Riemannian geometry, if we can find a transformation to turn a curved space into flat, then the original space is flat essentially. If we can not find such a transformation, the original space is a really curved space. Now, because we can find a transformation to turn (14) into (13), the metric (14) is flat essentially. Because we can not find a transformation to turn (2) into (13) when , the spatial part of (2) can not be flat!
, the spatial part of (2) can not be flat!
On the other hand, in order to make the spatial distance of the R-W metric be positive, we should have
 (15)
(15)
So we have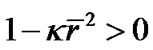 , i.e.,
, i.e.,  or
or . For the observable universe today, we have
. For the observable universe today, we have 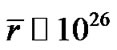 m. So for
m. So for , we should have
, we should have . Therefore, if
. Therefore, if  is a positive number, it should be very small. If the universe is infinite, we should have
is a positive number, it should be very small. If the universe is infinite, we should have . In the current cosmology, we take
. In the current cosmology, we take  and 1 as well as 0 to represent the different universes with negative and positive curvatures as well as flat individually. However,
and 1 as well as 0 to represent the different universes with negative and positive curvatures as well as flat individually. However,  is improper to describe the universe, for we have to take
is improper to describe the universe, for we have to take  to ensure the R-W metric meaningful. Unfortunately, this problem is completely neglected in the current theory.
to ensure the R-W metric meaningful. Unfortunately, this problem is completely neglected in the current theory.
2. The Spatial Curvature of the R-W Metric
Now let’s precisely calculate the curvatures of (10) under the condition  constant. As we know that curvature has concrete definition in mathematics. We should judge the flatness of space by strict calculation, not by apparent estimation. In the Riemannian geometry, the Riemannian curvature at a certain point of
constant. As we know that curvature has concrete definition in mathematics. We should judge the flatness of space by strict calculation, not by apparent estimation. In the Riemannian geometry, the Riemannian curvature at a certain point of  dimensional space is defined as [2]
dimensional space is defined as [2]
 (16)
(16)
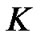 is related to the selections of direction vectors
is related to the selections of direction vectors  and
and  at each point in space. We define the covariant tensor
at each point in space. We define the covariant tensor 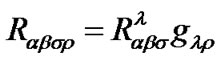 in which
in which  and
and  are calculated by following formulas
are calculated by following formulas
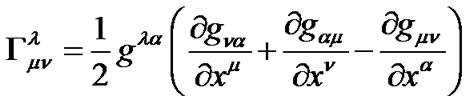 (17)
(17)
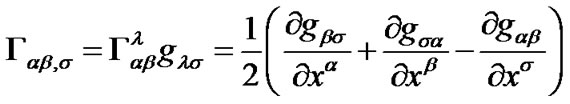 (18)
(18)
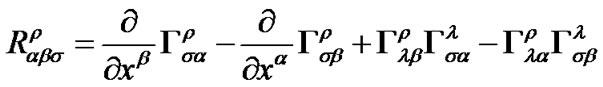 (19)
(19)
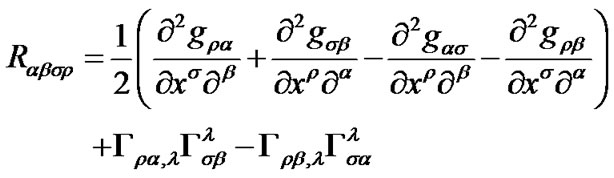 (20)
(20)
If curvatures are the same at all points in space, we have  constant with
constant with
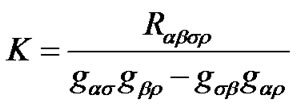 (21)
(21)
Further, if space is flat, the Riemannian-Christoffel tensors becomes zero everywhere with  or
or 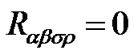 .
.
Now we calculate the space-time curvatures of the R-W metric. The non-zero Christoffel signs are
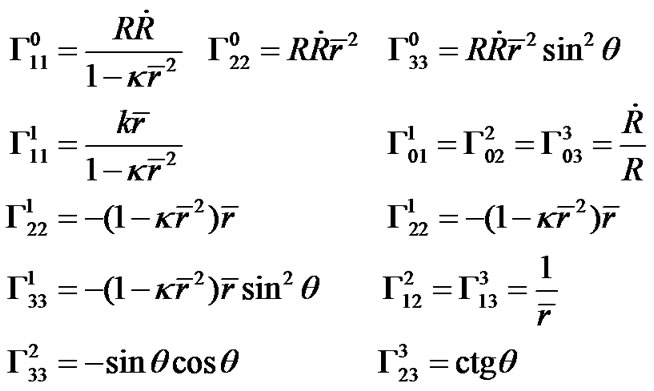 (22)
(22)
The non-zero curvature tensors of the R-W metric are
 (23)
(23)
The corresponding curvatures are
 (24)
(24)
Here  are the curvature of space-time crossing part, and
are the curvature of space-time crossing part, and  (
( ) are the curvatures of pure space. For
) are the curvatures of pure space. For , we take
, we take  or
or  constant. In this case,
constant. In this case,  becomes a constant. This is just the result that physicists think of the R-W metric at present. In order to make purely spatial curvature
becomes a constant. This is just the result that physicists think of the R-W metric at present. In order to make purely spatial curvature , we have two chooses. The first is to set
, we have two chooses. The first is to set  and
and  simultaneously, representing static space-time. Another is to set
simultaneously, representing static space-time. Another is to set  at certain moment
at certain moment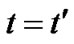 . In this case, we have
. In this case, we have 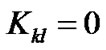 but still have
but still have . When
. When  but
but , we have
, we have . The result is completely different from the current understanding.
. The result is completely different from the current understanding.
Now let’s estimate the curvature’s magnitudes of the R-W metric. Taking  in (24), we get
in (24), we get
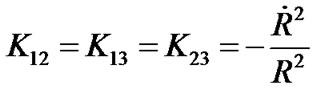 (25)
(25)
In cosmology, we define the Hubble constant  . At present moment
. At present moment , we have
, we have . So we have
. So we have , i.e., the spatial curvature of the expansive universe is very small. On the other hand, from the equation of cosmology, we have
, i.e., the spatial curvature of the expansive universe is very small. On the other hand, from the equation of cosmology, we have , so we have
, so we have . The curvature of crossing part of space and tine is also very small.
. The curvature of crossing part of space and tine is also very small.
Next, how do we recognize the spatial curvature of the metric (2)? In the Riemannian geometry, the intuitive picture is that when a vector moves along a loop and then returns to its starting point, if it can superimpose with original vector, the space is considered flat. If it can not, the space is curved. Therefore, if the space expands with time in the manner of the metric (2), a vector will not superimpose with the original vector when it moves along a loop and returns to the original point. We should recognize the space curvature of the metric (2) in this way.
However, the result of WMAP showed that the space of our universe seems nearly flat [3,4]. According to (24), the difference between constant  and
and  should be very mall at present moment. If we think that the constant
should be very mall at present moment. If we think that the constant  has same magnitude with
has same magnitude with , the spatial curvature of the expansive universe may be about
, the spatial curvature of the expansive universe may be about . As we know that the precision of WMAP is about
. As we know that the precision of WMAP is about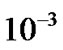 , so the experiment is unable to find such small curvature.
, so the experiment is unable to find such small curvature.
3. Influence on the Densities of Dark Material and Dark Energy
The result above may cause great influence on cosmology. By taking into account of cosmic constant , the Friedmann equation of cosmology is
, the Friedmann equation of cosmology is
 (26)
(26)
By defining the Hubble constant  and the effective material density of the universe
and the effective material density of the universe
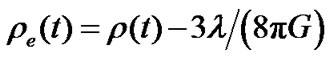 , we write (26) as
, we write (26) as
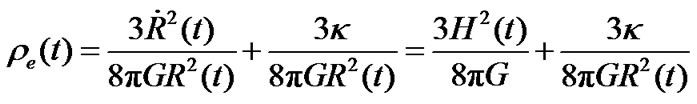 (27)
(27)
Let ,
,  ,
,  and define critical density
and define critical density , (27) becomes
, (27) becomes
 (28)
(28)
The formula is used to estimate the material density of the universe. If  represents space curvature factor, we have
represents space curvature factor, we have 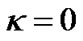 for the flat universe so that the current material density is equal to the critical density. Defining
for the flat universe so that the current material density is equal to the critical density. Defining , we have
, we have  for the universe today. However, observations indicate that we only have
for the universe today. However, observations indicate that we only have  for normal material, greatly less than 1. Therefore, non-baryon dark material and dark energy have to be introduced to fill the universe.
for normal material, greatly less than 1. Therefore, non-baryon dark material and dark energy have to be introduced to fill the universe.
However, if  is adjustable parameter, in stead of curvature factor, for the nearly flat universe and practically observed
is adjustable parameter, in stead of curvature factor, for the nearly flat universe and practically observed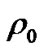 , we can chose proper
, we can chose proper 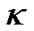 to satisfy (28). We take the Hubble constant
to satisfy (28). We take the Hubble constant  and obtain
and obtain  at present. By practical measurements, we have
at present. By practical measurements, we have  for luminous material [5-7]. Suppose that practical density of baryon material in the universe is about 10 times more than that of luminous material, i.e., suppose
for luminous material [5-7]. Suppose that practical density of baryon material in the universe is about 10 times more than that of luminous material, i.e., suppose
 , by taking
, by taking , we can make (28) to be satisfied.
, we can make (28) to be satisfied.
In this way, it becomes unnecessary for us to assume that the non-baryon material is about 6 times more than baryon material if they really exist. As for dark energy, it becomes surplus. We can make theory and observations consistent by adjusting the value of constant  without the hypotheses of dark energy. At last, if
without the hypotheses of dark energy. At last, if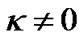 , from (27) we have
, from (27) we have
 (29)
(29)
It means that the Hubble constant is not only related to material density, but also relative to scalar factor. At present moment, we have . According to (28), we have
. According to (28), we have
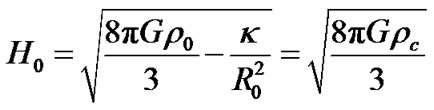 (30)
(30)
Therefore, the Hubble constant is the same.
In fact, if  is an adjustable parameter in stead of a curvature factor, many conclusions of the current cosmology should be re-evaluated. These problems will be discussed later.
is an adjustable parameter in stead of a curvature factor, many conclusions of the current cosmology should be re-evaluated. These problems will be discussed later.
4. Conclusions
By the strict calculation based on the Riemannian geometry, the paper proves that when the scalar factor  is related to time, the spatial curvature of the R-W metric is
is related to time, the spatial curvature of the R-W metric is , in stead of
, in stead of . That is to say, the R-W metric has no constant space curvature in general situations. Therefore, if the Friedmann equation is used to describe the expansionary universe, even space is flat, we can only consider
. That is to say, the R-W metric has no constant space curvature in general situations. Therefore, if the Friedmann equation is used to describe the expansionary universe, even space is flat, we can only consider  as an adjustable and non-zero parameter. The result may greatly impact cosmology. We need to re-estimate the values of dark material and dark energy densities.
as an adjustable and non-zero parameter. The result may greatly impact cosmology. We need to re-estimate the values of dark material and dark energy densities.
According to the current estimation in cosmology, normal baryon material only makes up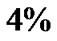 , non-baryon dark material makes up
, non-baryon dark material makes up 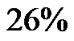 and dark energy makes up
and dark energy makes up  of the universal material. However, nonbaryon dark material with such huge amount of quantity can not been found up to present days, though physicists have struggled to find it for decades.
of the universal material. However, nonbaryon dark material with such huge amount of quantity can not been found up to present days, though physicists have struggled to find it for decades.
The situation is even more puzzling for dark energy. In fact, the concept of dark energy is similar to the concept of ether in the nineteen century. Classical physics could not explain the light’s propagation in the universal vacuum so that the concept of ether as a medium had to be introduced. One purpose that Einstein putted forward special relativity was to eliminate the concept of ether from physics.
Time goes into the twenty-first century, the history is repeating. Because physicists can not explain the high red-shift of supernovae, the concept of dark energy has to be introduced. By the correct understanding of the constant  in the R-W metric and the Friedmann equation, we no longer need the concept of dark energy again. Meanwhile, we may not need to assume that non-baryon dark material is 6 times more than normal baryon material, if non-baryon dark material exists actually. In this way, we may overcome the current puzzling situation of cosmology thoroughly.
in the R-W metric and the Friedmann equation, we no longer need the concept of dark energy again. Meanwhile, we may not need to assume that non-baryon dark material is 6 times more than normal baryon material, if non-baryon dark material exists actually. In this way, we may overcome the current puzzling situation of cosmology thoroughly.
[1] S. Weinberg, “Gravitation and Cosmology,” Science Publishing Company, 1984, p. 441.
[2] S. Zhiming, “Tensor in Physics,” Beijing Normal University Publishing Company, Beijing, 1985, p.180.
[3] P. de Bernardis, et al., “A High Spatial Resolution Analysis of the MAXIMA-1 Cosmic Microwave Background Anisotropy Data,” Nature, Vol. 404, 2000, pp. 955-959. doi:10.1038/35010035
[4] C. L. Merriment, et al., “Wilkinson Microwave Anisotropy Probe (WMAP), Observations: Temperature-Polarization Correlation, Astrophysical Journal Supplement Series, Vol. 148, No. 1, 2003, pp. 195-211.
[5] J. H. Oort, “In La Struccture et Evolution de Univers, Institute International de Physique Solvay,” R. Stoops, Brussles, 1958, p. 58.
[6] R. G. Carlberg, et al., “Galaxy Cluster Virial Masses and Omega,” Astrophysical Journal, 1996, Vol. 462, pp. 32- 49. doi:10.1086/177125
[7] D. N. Schramm, M. S. Furner, “Big-Bang Nucleosynthesis Enters the Precision Era,” Reviews of Modern Physics, Vol. 70, No. 1, 1998, pp. 303-318. doi:10.1103/RevModPhys.70.303
Appendix: The Curvatures of Two Dimensional Curved Surfaces in the Three Dimensional Flat Space
Because the geometrical figure of three dimensional supper spherical surface is abstract and not visualized easily, in order to have a direct visualization, we discuss two dimensional curved surfaces in three dimensional flat spaces further in this section. Similar to (3) and (4), the metric of three-dimensional flat space and the condition of spherical surface are individually
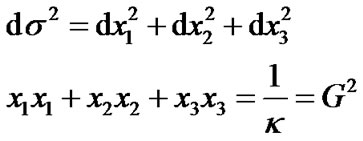 (31)
(31)
Here constant 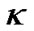 is the curvature and
is the curvature and  is the radius of two dimensional spherical surface. By using column coordinates
is the radius of two dimensional spherical surface. By using column coordinates ,
,  and
and , (31) becomes
, (31) becomes
 (32)
(32)
Here  is the radius of a circle on the plane
is the radius of a circle on the plane  constant. According to the same calculation procedure, we have
constant. According to the same calculation procedure, we have
 (33)
(33)
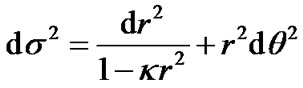 (34)
(34)
The form of (34) is similar to (6). We see that the metric of (32) is flat, but the metric of (34) becomes curved. The reason is that the transformation (33) is non-linear. That is to say, non-linear transformations may change spatial curvatures. Similarly, by introducing nonlinear transformation  and let
and let  in (34), we obtain
in (34), we obtain
 (35)
(35)
Let
 (36)
(36)
and substitute (35) in (36), we get
 (37)
(37)
The form of (37) is similar to that of (12). The equations corresponding to (8) and (9) are
 (38)
(38)
 (39)
(39)
It is obvious that the curvature of (39) can not be constant 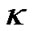 when
when  constant. In fact, by considering
constant. In fact, by considering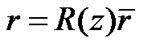 , the spherical surface Equation (32) becomes
, the spherical surface Equation (32) becomes
 (40)
(40)
Because new variables are  and
and , (40) is not the equation of spherical surface and constant
, (40) is not the equation of spherical surface and constant  is no longer curvature. When
is no longer curvature. When  constant, according to (40), we have
constant, according to (40), we have
 (41)
(41)
Only in this case, constant  represent the curvature of circle with radius
represent the curvature of circle with radius 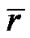 on the plane
on the plane  constant. Similarly, by using
constant. Similarly, by using  in supper spherical surface equation (4), we obtain
in supper spherical surface equation (4), we obtain
 (42)
(42)
Because new variables are  and
and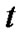 , (42) is not the equation of three dimensional supper spherical surface and the constant
, (42) is not the equation of three dimensional supper spherical surface and the constant  is no longer curvature again. When
is no longer curvature again. When  constant, we have
constant, we have
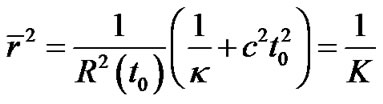 (43)
(43)
Only in this case, constant  can be considered as the curvature of supper spherical surface with radius
can be considered as the curvature of supper spherical surface with radius .
.
We calculate the curvature tensor of the metric (38). The non-zero metric tensors of (38) are
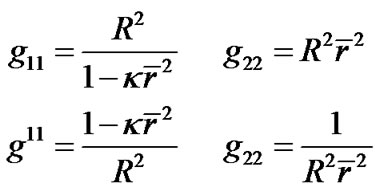 (44)
(44)
The non-zero Christoffel signs are
 (45)
(45)
According to (20), the only non-zero curvature tensor is
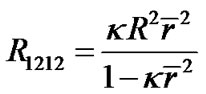 (46)
(46)
So according to the formula (16), the Riemannian curvature of (38) is
 (47)
(47)
That is to say, the curvature of (38) is , rather then
, rather then . In fact when
. In fact when  constant, let
constant, let  in (38), we get (34).
in (38), we get (34).
Next, we calculate the curvature of (39). We consider  as
as . The metric tensors of (39) are
. The metric tensors of (39) are
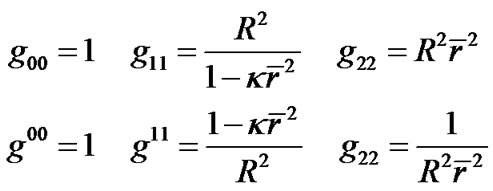 (48)
(48)
The non-zero Christoffel signs are
 (49)
(49)
The non-zero curvature tensors are
 (50)
(50)
According to (16), we have
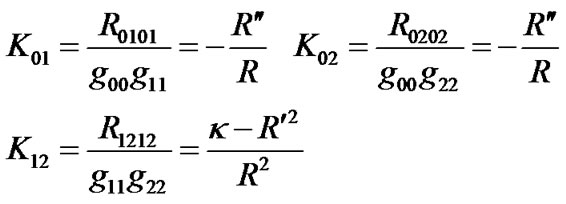 (51)
(51)
Because  contains
contains , the result is different from (47). It means that the spatial curvatures of (38) and (39) are different. It implies that the dimensions of space can change curvature, despite that the metric form (39) of two dimensional curved surface is completely the same as (38). In fact, as we know that the metric
, the result is different from (47). It means that the spatial curvatures of (38) and (39) are different. It implies that the dimensions of space can change curvature, despite that the metric form (39) of two dimensional curved surface is completely the same as (38). In fact, as we know that the metric  is flat with zero curvature, but
is flat with zero curvature, but 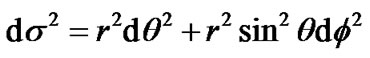 is curved with curvature
is curved with curvature . Related to the radius of spherical surface, the curvature is not a constant.
. Related to the radius of spherical surface, the curvature is not a constant.