1. Introduction
The electromagnetic Poynting vector has long been of considerable interest over the years [1–9]. This is so because it is directly related to the electromagnetic (EM) energy flux and the electromagnetic linear momentum. In recent years, the role of EM linear momentum in total momentum balance has attracted the attention of many authors [10–16]. Furthermore, the EM energy flux carried by the Poynting vector has been the subject of many workers in the context of energy conservation in electromagnetic systems [17–21]. In recent years, it was shown that when a charged capacitor is connected to another uncharged identical one, exactly half the stored energy disappears after the equilibrium state is achieved. This also happens when a capacitor is charged by a battery, where only half the supplied energy is stored in the capacitor. This pedagogical problem has been a topic of interest by several authors [22–27]. When dealing with energy conservation in EM systems, one has to consider all the possible channels through which energy is transported through as the system transforms from an initial non-equilibrium to a final equilibrium state. For example, it was shown [23] that when charging a capacitor half the work done by the power source is stored in the capacitor while the other half is carried by the Poynting vector which crosses the surface of the connecting wires. The purpose of this paper is to shed some light on the dynamics of the electromagnetic momentum and the energy needed when an electromagnetic system transforms from non-equilibrium to equilibrium states. This gives a fruitful and an illustrative example to students in electrodynamics course and helps them for a deep understanding of basic concepts in the subject. To that end, we consider an infinitely long solenoid which is fed by a current that varies linearly in time for a time period T after which it reaches its final constant value. The paper is organized as follows: In Section 2, we consider the electromagnetic momentum. In Section 3, we examine electromagnetic energy. Section 4 is devoted for conclusions.
2. Electromagnetic Momentum for an Ideal Solenoid
We consider an infinitely long solenoid (ideal) of radius R and with number of turns per unit length n. The purpose is to examine the dynamics of the linear momentum balance during a time period, say T, through which the current is linearly increasing towards its final constant value, say I0. Our system is assumed to be force-free which means that the total linear momentum (mechanical momentum and electromagnetic momentum) is constant, which could be taken to be zero. Therefore, we assume that the battery connected to the solenoid gives a time-dependent current  given by:
given by:

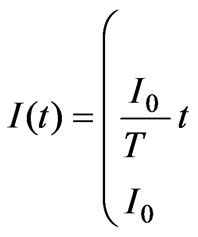 (1)
(1)
Faraday’s law of induction suggests an induced electric field whose value satisfies its integral form
 (2)
(2)
where  is the induced electric field and
is the induced electric field and  is the magnetic flux inside the solenoid.
is the magnetic flux inside the solenoid.
Choosing a circular loop of radius r inside the solenoid, and using , for the magnetic field inside the solenoid, one gets
, for the magnetic field inside the solenoid, one gets
 (3)
(3)
and thus

 (4)
(4)
The Poynting vector inside the solenoid, during the time T, is given by
 (5)
(5)
and therefore the electromagnetic linear momentum density is
 (6)
(6)
The total electromagnetic linear momentum,  , can be computed as follows: writing
, can be computed as follows: writing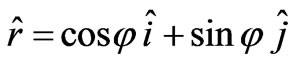 , we get
, we get
 = 0(7)
= 0(7)
since the  integral vanishes. Equation (6) gives a force density
integral vanishes. Equation (6) gives a force density
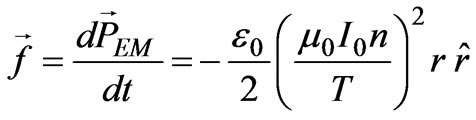 (8)
(8)
which gives a vanishing total force once the integration over  is carried out. This force density is needed to bend the current in its circular loops that, due to inductive inertia, otherwise would move in a straight line. As we will see in a moment, the reaction force density (hidden force density as we will see shortly) to the above force density causes the radius of the circular loop to increase. So our result shows that during the period T, through which the current is increasing, the total electromagnetic momentum and the total force are both zeros but yet they have non-vanishing density values that are directed towards the axis of the solenoid. This result needs explanation since initially (for
is carried out. This force density is needed to bend the current in its circular loops that, due to inductive inertia, otherwise would move in a straight line. As we will see in a moment, the reaction force density (hidden force density as we will see shortly) to the above force density causes the radius of the circular loop to increase. So our result shows that during the period T, through which the current is increasing, the total electromagnetic momentum and the total force are both zeros but yet they have non-vanishing density values that are directed towards the axis of the solenoid. This result needs explanation since initially (for ) the system has no momentum density. We show below that the electromagnetic linear momentum density is exactly balanced by hidden momentum density that arises during the time period T. Assuming the solenoid has a radius R with its axis aligned along the z-axis and the current flows counterclockwise (+
) the system has no momentum density. We show below that the electromagnetic linear momentum density is exactly balanced by hidden momentum density that arises during the time period T. Assuming the solenoid has a radius R with its axis aligned along the z-axis and the current flows counterclockwise (+ direction), then following Babson et al. [28], the hidden momentum (which is of relativistic origin) is given by
direction), then following Babson et al. [28], the hidden momentum (which is of relativistic origin) is given by
 (9)
(9)
where  is the magnetic dipole moment of the current loop(s) and
is the magnetic dipole moment of the current loop(s) and  is the electric field. Now, for a length
is the electric field. Now, for a length  of the solenoid, the number of turns is
of the solenoid, the number of turns is  and thus the magnetic dipole moment
and thus the magnetic dipole moment . Using Equation (4) for the induced electric field, with
. Using Equation (4) for the induced electric field, with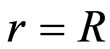 , we get
, we get
 , (10)
, (10)
where we used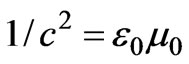 . Therefore, the hidden momentum density is
. Therefore, the hidden momentum density is
 (11)
(11)
which exactly cancels the electromagnetic linear momentum density at the loops of the solenoid, as can be seen from Equation (6) with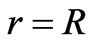 . Back to the force density given in Equation (8), this force density is related to the pressure gradient. As it was shown in [28], the relativistic relation between the force density and the pressure gradient is
. Back to the force density given in Equation (8), this force density is related to the pressure gradient. As it was shown in [28], the relativistic relation between the force density and the pressure gradient is
 (12)
(12)
where  is the usual Lorentz factor. It is interesting to note that the time derivative of the hidden momentum density (given in Equation (11)) gives the so-called the hidden force density which is exactly the negative of the force density evaluated at the surface of the solenoid,
is the usual Lorentz factor. It is interesting to note that the time derivative of the hidden momentum density (given in Equation (11)) gives the so-called the hidden force density which is exactly the negative of the force density evaluated at the surface of the solenoid, ( see Equation (8)). Therefore, at any time t during the time period T, the electromagnetic force density is exactly canceled by the hidden force density.
( see Equation (8)). Therefore, at any time t during the time period T, the electromagnetic force density is exactly canceled by the hidden force density.
2. Energy Considerations
The purpose of this section is to examine energy balance which is involved in the process of establishing a current in an infinite solenoid. It is well-known that the stored magnetic energy in a length  of an infinite solenoid that carries a current
of an infinite solenoid that carries a current  is
is
 (13)
(13)
where we used Equation (1) and the self-inductance , for a length
, for a length of the solenoid. When the current reaches its final value
of the solenoid. When the current reaches its final value , at
, at , the stored magnetic energy becomes
, the stored magnetic energy becomes
 (14)
(14)
The question to be answered is how much work is needed to be done by the power supply in order to store the magnetic energy given in Equation (14). During the time – period T, the electromagnetic power per unit area that crosses the surface of the solenoid is given by the Poynting vector  evaluated at the solenoid's surface. Thus using Equation (5) with
evaluated at the solenoid's surface. Thus using Equation (5) with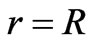 , we get
, we get
 (15)
(15)
The electromagnetic energy 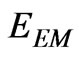 that is transmitted inside a length
that is transmitted inside a length  of the solenoid is
of the solenoid is

 (16)
(16)
which has the same magnitude as the stored magnetic energy given in Equation (14). Therefore, the energy that was carried by the Poynting vector has been stored as magnetic energy inside the solenoid. To see other forms of energy involved in the process of establishing the current in the solenoid, the time-dependence of the magnetic field gives an induced electromotive force ( ).This induced electromotive force is given by Faraday's law, namely
).This induced electromotive force is given by Faraday's law, namely
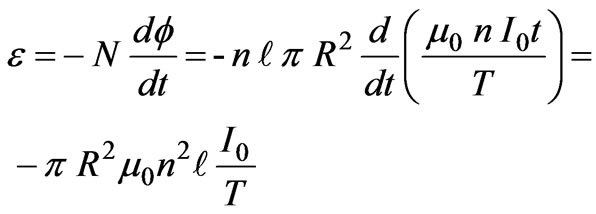 (17)
(17)
The power done by this induced electromotive force is thus
 (18)
(18)
and therefore, the work done is

 (19)
(19)
The above Equation clearly shows that the work done by the power supply against the induced electromotive force (which is the negative of Equation (19)) is exactly equal to the stored magnetic energy given by Equation (14). Therefore, the total energy delivered by the power supply is twice the stored magnetic energy. It should be emphasized that the work done against the induced electromotive force is necessary for the current to reach its final equilibrium value. So our result shows that the stored magnetic energy (which is exactly half the work done by the power supply) comes from the Poynting vector that crosses the surface of the solenoid. The other half of the work done is the price that one must pay in order to achieve a final equilibrium state for the current. This other half of the work done finds its way as work done against the induced electromotive force in the windings of the solenoid.
This is exactly analogue to the case of charging a capacitor by a power supply, in which it was shown [23] that the stored electric energy in the capacitor comes from the energy carried by the Poynting vector that crosses the plates of the capacitor, and this energy is exactly half the energy delivered by the power supply. While the other half is carried by the Poynting vector that crosses the connecting wires. Another analogue case is the two capacitor problem: When a charged capacitor is connected to an uncharged one with the same capacitance, exactly half the stored energy disappears after the charge transfer is completed. In these analogue cases, it was noted in earlier work that if the presence of nonzero resistance in the circuit is assumed, the amount of Joule heat loss in the resistor becomes exactly the same as the missing energy [29]. Others [25,27,30] used superconducting wires and have tried different mechanisms to explain this energy loss and they arrived at the same conclusion. Another example in mechanics: if a particle collides, in a completely inelastic collision, with another stationary particle of the same mass then exactly half the initial kinetic energy will be lost in the collision. Our solenoid problem is another one, but here the energy loss is due to the work done against the induced electromotive force. Therefore, regardless of the nature of the mechanism, the amount of the energy loss should always be exactly half the supplied energy of the power supply. It must be emphasized that this energy loss, in all the above cases and possible similar ones, is necessary (or the price that one must pay) to transform the system from an initial non-equilibrium state to a final equilibrium one [23,26]. We must note that our results do not change if one chooses a different function for the current, in which case the reader can easily verify this.
4. Conclusions
We considered an infinite solenoid which is fed by a current that increases linearly in time over a time period T, after which the current reaches its final value. Our results showed that during that period, the electromagnetic linear momentum density is exactly balanced by the hidden momentum density. In other words, the electromagnetic force density is exactly balanced be the hidden force density. This keeps the total linear momentum density and the total force density zeros at any time during that period. Which is consistent with the situation before the current is turned on. It was also shown that the stored magnetic energy inside the solenoid is exactly half the energy delivered by the power supply. This stored magnetic energy is just the energy which is carried by the Poynting vector that crosses the surface of the solenoid. The other half is consumed against the induced electromotive force which is needed to transfer the system to a final equilibrium state. The system we considered is analogue to other systems: In the process of charging a capacitor by a power supply, half the energy delivered by the power supply appears as electric energy in side the capacitor. In the two capacitor problem, half the initial energy is lost (when the capacitances of the two capacitors are the same). In mechanics, the completely in-elastic collision is another example, in which half the initial kinetic energy is lost when an incident particle collides with another stationary similar particle. In our present solenoid problem and in all the above mentioned systems, the missing energy is necessary in order to transfer the system from an initial non-equilibrium state to a final equilibrium state.