A Fundamental Equation of Thermodynamics that Embraces Electrical and Magnetic Potentials ()
1. Introduction
A simple experiment was run on a control mass that encloses a permanent magnet immersed in a water basin. The magnet was allowed to attract iron-balls moving steadily toward the magnet along an inclined plane. The results of such experiment show a reduction in the temperature of the water. Such decrease in temperature or internal energy of the magnet and the system is considered as a result of a work done by the magnet on the moving balls. So, it is possible to postulate the magnetic flux as a form of energy or electromagnetic waves similar to the heat emitted from a hot body. Reviewing Faraday’s discovery when inserting dielectric slabs between the plates of a condenser, the energy stored in the capacitor circuit decreased by the same ratio of increase of the electric charge on the condenser plates [1]. Such result proves also that the electric charge transferred to the dielectrics increases by the same ratio the stored energy of the inserted dielectrics.
According to Maxwell’s comments regarding his equations [2], electricity and magnetism were supposed to be of a wave-like nature as the electromagnetic waves since an oscillating electric field generates an oscillating magnetic field and the oscillating magnetic field in turn generates an oscillating electric field, and so on. In former researches [3,4], it was discussed also common features of the magnetic flux and electric charges. In this article, it is reviewed the similarities between laws characterizing electric charges, magnetic flux and heat flow to prove, analytically, their identity as special categories of electromagnetic waves. The processing of substances in magnetic refrigeration cycles led to a defined description of the produced magnetic-hysteresis in terms of increase of the system’s entropy and temperature [5]. Similarly, thermodynamic work required to separate solutions during capacitive deionization processes is fully expressed in terms of decrease of the system’s entropy [6]. According to such conclusions; it is possible to postulate the magnetic flux and electric charges in terms of entropy change times a corresponding potential by analogy to heat flux which is expressed in terms of temperature, as a thermal or heat potential, and the corresponding change of entropy. Introducing such postulates into the first law of thermodynamics led to a fundamental equation that embrace electric charge and magnetic flux as mechanisms of energy transfer and that proved its “trueness”.
Many references defined the time’s arrow as a property of entropy alone [7]. According to such definition, the time coordinate in Maxwell Equations and solutions was fuzzily substituted by entropy. Accordingly; the areas bounded by the oscillating electrical and magnetic potentials in the electromagnetic waves could represent the electrical and magnetic energy imparted by such electromagnetic waves. Such approach helped in postulating the electric charges and magnetic flux as special categories of electromagnetic waves of assigned potentials. Such postulates offer many plausible explanations for phenomena in the fields of thermodynamics and electromagnetism [8] as the magnetic expansion [9], Kerr effect [10] and the phenomena of discharge of clouds, colours of charges and magnetic dipole moments.
2. Experimental Analysis of the Magnetic Flux
As an approach to prove similarity of the heat emitted from a hot body and the magnetic flux emitted from a magnet; a permanent magnet was immersed in an insulted water basin and was allowed to attract polished iron balls of along an inclined smooth glass plane, Figure 1. The temperature of water was recorded. As the magnet performed a mechanical work, a decrease in the water temperature was measured by a digital thermometer. By applying the first law of thermodynamics on the magnet-water closed-system [11], we get the following equation:
 (1)
(1)
where CF is the flask’s heat capacity, n is the number of attracted balls along the inclined plane per unit time, mb is the mass of any iron ball, g is the gravity acceleration, s is the length of the path of the irons ball along the inclined smooth plate; φ is angle of inclination of the smooth plate and ∆t is the change of temperature during the time interval “ ”.
”.
(Experimental data: thermal capacity of the flask = 1.26 kJ/ deg, mass of each iron ball = 0.3 kg, number of attracted balls per minute = 42 balls, s = 20 and  = 30 deg.)
= 30 deg.)
Figure 2 shows the results as calculated from Equation (1) and as recorded during the attraction process. As a conclusion, there is a loss of the magnet’s internal energy during attraction of the iron balls. Such energy was substituted by decrease in the temperature or internal energy of the system. Such conclusion proves the behavior of a magnet emitting magnetic flux is similar to a hot body emitting heat or electromagnetic radiation. So, the magnetic flux may be considered as a form of energy or electromagnetic waves.
3. Analysis of Electric Flux
According to the Faraday’s discovery [1], when the space

Figure 1. Measurement of magnet’s work during attraction of iron balls
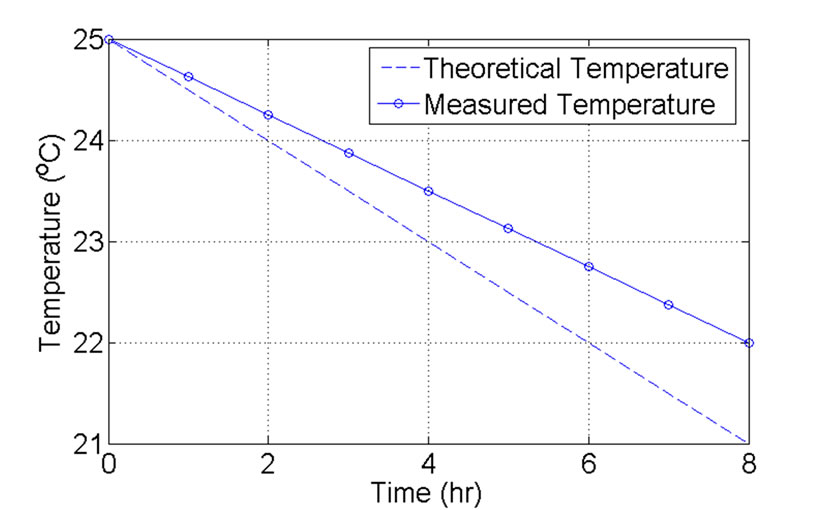
Figure 2. Measurement and calculation results of the system temperature
between the capacitor plates was filled by a dielectric material, the capacitance of the capacitor increased by a dielectric constant  defined as follows:
defined as follows:
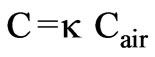 (2)
(2)
Faraday found also that the addition of such dielectric material between the plates increased the initial charge on the plates of a capacitor,  to a final value
to a final value  defined by the equation [1]:
defined by the equation [1]:
 (3)
(3)
By comparing the initial and final energies stored in the capacitor’s circuit, 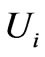 and
and  , it was found that the initial energy decreased by the same coefficient
, it was found that the initial energy decreased by the same coefficient 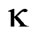 according to the equation [12]:
according to the equation [12]:
 (4)
(4)
According to Equations (3) and (4); the coefficient κ equals the ratios of increase of the electric charge on the capacitor plates and the decrease of the internal energy of the capacitor circuit due to insertion of the dielectric material. Such result shows that the loss of the stored energy in the capacitor circuit is absorbed as an electric charge on the capacitor plates. According to the energy – conservation principles; the electric charge can be considered as a form of energy that is transferred to or from the dielectrics and causes the simultaneous increase of the capacitor charge and decrease of the internal energy of its circuit.
4. Maxwell Waves
Regarding the origin of the electromagnetic wave equations; Maxwell combined displacement current with some of the other equations of electromagnetism and obtained a second-order partial differential equation that describes the propagation of electromagnetic waves through free space or a medium. The homogeneous form of such equation is written in terms of the electric field E and the magnetic field B as follows [12]:
 (5)
(5)
 (6)
(6)
where c is the speed of light in the free space (c = 299,792,458 m/second), and t is the time.
The general solution of such electromagnetic wave equation is a linear superposition of waves of the form [13]
 (7)
(7)
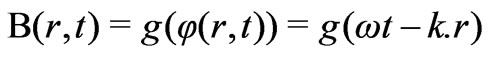 (8)
(8)
Virtually, both forms represent a well-behaved function “g” of dimensionless argument “ ” where
” where
 : is the angular frequency (in radians per second), and k: is the wave vector (in radians per meter).
: is the angular frequency (in radians per second), and k: is the wave vector (in radians per meter).
In addition, for a valid solution, the wave vector and the angular frequency are not independent; they must adhere to the dispersion relation [13]:
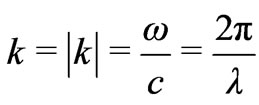 (9)
(9)
where: k is the wave number and  is the wavelength.
is the wavelength.
Maxwell commented the results of his solutions as follows; the agreement of the results seems to show that light and magnetism are affections of the same substance, and that light is an electromagnetic disturbance propagated through the field according to electromagnetic laws [12]. Such comment considers magnetism of the same substance as electromagnetic waves. Similarly, Maxwell derived a wave form of the electric and magnetic equations, revealing a wave-like nature of electric and magnetic fields. According to Maxwell [13], electricity and magnetism were considered of a wave-like nature as electromagnetic waves, since an oscillating electric field generates an oscillating magnetic field and the magnetic field in turn generates an oscillating electric field, and so on. Finally; according to Maxwell comments electric charge and magnetic flux may be considered also as forms of electromagnetic waves or energy as they are components of such waves.
5. Similarity of Fluxes
Energy is restricted in this research to the heat radiation propagating as electromagnetic waves or, according to quantum mechanics, as photons. Similarities between such forms of energy as heat, electric charge and magnetic flux are primarily found into their common quantization and conservation properties. The energy is generally quantized into photons of quanta v, where h is the Planck’s constant [13,] which is conserved according to principles of energy conservation. The electric charge is quantized and conserved too. The elementary charge of a single electron or proton is found experimentally as follows [12]:
e = 1.60 × 10- 19 CoulombIt is found that any positive or negative charge q show has a quantized value that is expressed as follows [12];
q = ne, where n = ±1, ±2, ±3,…(n∈Z)(10)
The fact that electric charge is quantized may be considered as one of the most profound mysteries of the physical world. However, considering the charge as a form of energy, which are naturally quantized, removes such mystery. Similarly, it is found that the charge is conserved as the net charge in a system or object is preserved too.
The magnetic flux is also quantized into quanta expressed generally as [12]:
 ±1, n = ±2, n = ±3
±1, n = ±2, n = ±3  (11)
(11)
It is also found that many laws characterizing energy transfer, as heat, are similar to the laws that characterize the transfer of electric charges and the magnetic flux. The heat transfer by conduction is expressed as [14]:
 (12)
(12)
Similarly, the charge transferred is expressed by Ohm’s law as [11]:
 (13)
(13)
Equations (12) and (13) show an analogy between the energy transfer by heat and electricity. Heat transfer in the first equation is driven by the difference in temperature and in the second equation the charge transfer is driven by the difference in electrical potentials. However, the laws concerning the transfer of magnetic flux are not yet formulated, but there is an approach to its formulation as a magnetic flux emergence in the sun is directly traced on the solar surface (in visible-white light) by the presence of dark, mainly round-shaped areas, called sunspots, surrounded by brighter regions of higher magnetic potential called plagues [15]. Measurements of magnetic fields at the solar surface shows that sunspots tend to be grouped in pairs, one with positive and one with negative magnetic polarity which may be characterized by flow of magnetic flux according to similar equations as Equations (12) and (13). Such similarities between heat, electric charge and magnetic flux prove they are forms of energy or electromagnetic waves.
6. A Fundamental Energy Equation
The first and second laws of thermodynamics may lead to a fundamental equation of thermodynamics in the form [14]
 (14)
(14)
where:
 : Change in internal energy of a T.D. system;
: Change in internal energy of a T.D. system;
 : Thermal Energy imparted to a system represented as the product of the temperature and the change of entropy;
: Thermal Energy imparted to a system represented as the product of the temperature and the change of entropy;
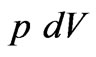 : work of expansion of volume (
: work of expansion of volume ( ) under the pressure p;
) under the pressure p;
 : energy imparted by new surface area formation
: energy imparted by new surface area formation  at the surface tension
at the surface tension ;
;
 : work of chemical change
: work of chemical change  at given chemical potential
at given chemical potential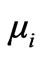 .
.
However, Equation (14) does not include the magnetic energy that may be transferred to any system. In addition, its R.H.S. includes the term “E de” that corresponds to the electric energy imparted to the system. This term assumes the parameters “E” and “e” are properties that define the state of a general thermodynamic system and de is an exact differential or a differential of a property. According to former analysis, the electric charges “e” transferred to the system represent energy in transfer of a similar nature as heat and it should not be considered as a property of a thermodynamic system. So, Equation (15) is incorrect according to the principles of thermodynamics.
Introducing the electric charge, magnetic flux and heat flux as mechanisms of energy transfer to a thermodynamic system; a modified form of Equation (14) can be written as follows:
 (15)
(15)
The processing of substances in magnetic refrigeration cycles leads to a defined description of the produced magnetic hysteresis in terms of an entropy increase and the system temperature [4]. So, temperature and entropy changes were actually achievable by the flow of magnetic flux into a system. In this context, the fact that the working material displays hysteresis [16], calls for a better physical understanding of the role of irreversibility in the magnetization process. Such understanding can be based on describing the magnetic flux by similar terms as heat flux, i.e. in terms of magnetic potential times a corresponding entropy increase. Such representation removes the ambiguity found in Bill queries [9]. Similarly; revising the work of Biesheuvel in the thermodynamic cycle analysis of capacitive deionization, [6], where the thermodynamic work required in solutions separation during capacitive deionization processes was fully utilized to decrease the entropy of the system. Such analysis implements also the expression of the electric charge in terms of the product of electric potential times the corresponding entropy increase.
According to the second law of T.D., the flow of heat into a system generates an entropy increase of such system expressed by the relation [10]:
 (16)
(16)
According to the previous analysis and the derived similarities, the electric charge can be expressed by a similar expression as follows.
 (17)
(17)
where Qelect is electric charge imparted to a system, E is the electrical field intensity or potential, in analogy to temperature as the thermal potential, and dSelectric is the entropy increase associated by such transferred electric energy or charge.
According to modern literatures [12], the term “B” represents the magnetic flux density. However, such density can be assumed proportional to the magnetic field intensity, H, according to the following relation (in free space) [12]:
 (18)
(18)
where  is called permeability of free space or magnetic space constant. Such direct proportionality allows introducing the magnetic field intensity to replace the magnetic flux density in Maxwell’s solution which is analogous to the electric field intensity.
is called permeability of free space or magnetic space constant. Such direct proportionality allows introducing the magnetic field intensity to replace the magnetic flux density in Maxwell’s solution which is analogous to the electric field intensity.
So, the magnetic flux can be expressed as follows:
 (19)
(19)
where  is the magnetic flux imparted to a system, H is the magnetic field intensity and
is the magnetic flux imparted to a system, H is the magnetic field intensity and  is the generated entropy by the transferred magnetic flux. By substituting Equations (16), (17) and (19) into Equation (14); a modified fundamental equation of thermodynamics can be expressed as follows:
is the generated entropy by the transferred magnetic flux. By substituting Equations (16), (17) and (19) into Equation (14); a modified fundamental equation of thermodynamics can be expressed as follows:
 (20)
(20)
where
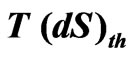
,

and

correspond to the thermal, electric and magnetic energies imparted to the system, respectively, and

,

and

represent the entropy productions by the corresponding transferred thermal, electric and magnetic energies. The main corollary of such fundamental equations is the possibility of representing the electric charges transferred or imparted to a system into an E-s diagram and the magnetic flux imparted to a system into an H-s diagram similar to the T-s diagram that represent the heat transferred to such system.
7. Maxwell Equations
The arrow of time is found as property of entropy alone [7]. Accordingly; time in Maxwell Equations (5) and (6) may be replaced by entropy. Such transformation leads to modified solutions of Maxwell equations that may be stated as follows:
 (21)
(21)
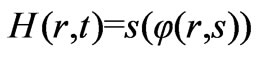 (22)
(22)
Accordingly, the electromagnetic waves can be represented in E-s and B-s planes by replacing the time axis in Figure 3 by entropy. In such representation; the areas enclosed by the oscillating fields, electric or magnetic, represents the imparted electric and magnetic energies as postulated in Equations (17) and (19).
Searching for a plausible answer of a frequently asked question: If the electromagnetic waves are considered, according to the quantum mechanics, as photons; then, how the photon can have a charge or a magnetic polarity [14]? The answer implements a modified solution of Maxwell Equations which is not identical to that stated by Equations (7) and (8). In the following solution it is assumed a non-zero initial electrical potential “ ” in the electric component of the electromagnetic wave. Hence, the following solution may satisfy the postulated Maxwell’s Equations (21) and (22), where the time is replaced by entropy:
” in the electric component of the electromagnetic wave. Hence, the following solution may satisfy the postulated Maxwell’s Equations (21) and (22), where the time is replaced by entropy:
 (23)
(23)
 (24)
(24)
Such solution assumes some categories of electromagnetic waves whose electric potential is oscillating around a specified value of non-zero electric potential but its magnetic potential is oscillating about a zero magnetic potential. The graphical representation of such solution is seen in Figures 4 and 5, where Figure 4 represents a positive charge and Figure 5 represents a negative charge.
The net charge in each imparted sinusoidal wave has a value which may be positive or negative according to the sign of the charge found by the following integral in a complete wave:
 (25)
(25)
The given integration may represent an electric charge of a positive or negative potentiality according to the direction of the wave oscillations if it is around positive or negative values of .
.

Figure 3. Electromagnetic waves in E-s and H-s planes

Figure 4. Graphical representation of a positive electric charge

Figure 5. Graphical representation of a negative electric charge
Similarly, it is assumed in the following solution a non-zero initial magnetic potential “ ” in the magnetic component of the electromagnetic wave. So, the following modified Maxwell’s solution may represent flow of magnetic flux:
” in the magnetic component of the electromagnetic wave. So, the following modified Maxwell’s solution may represent flow of magnetic flux:
 (26)
(26)
 (27)
(27)
Such solution is represented graphically in Figure 6 where the net bounded area has a non-zero magnetic potential. So, the net magnetic flux in each imparted sinusoidal wave has the value:
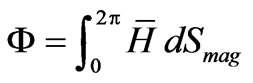 (28)
(28)
So, the postulated solutions of Maxwell Equations and the introduced definitions of electric charges and heat flux assign definite potentials for such fluxes in terms of (

) and (

), with definite polarity or direction. The units of the electric charge or the magnetic flux are stated as forms of energy in Joules. Hence the units of dS
elect and dS
mag will be in Joule/Volt and Joule/Oersted respectively in analogy to the units of dS
thermal in Joule / K [6]. Such definitions remove confusions in the units of magnetism and electricity.
8. Reviewing the Introduced Fundamental Equation
As previously mentioned, the definitions of the electric charge and magnetic flux, as modified forms of EM waves, can be directly concluded from Maxwell’s statements and the similarity of the laws governing such entities. However, such definitions introduce also plausible explanations to many discovered phenomena. The definition of the electric charge as electromagnetic waves explains the behavior of the cathode rays as waves in the famous Crookes tube [15], where the cathode rays, defined previously as flow of electric charges or electrons,

Figure 6. Graphical representation of magnetic flux
travelled in straight lines, produce a shadow when obstructed by objects and the rays could pass through thin metal foils without disturbing them (Tested by New Zealander Ernest Rutherford using gold foil [15]). Hertz maintained it also was a wave. Hence, the introduced definition of electric charge as a flow of modified EM waves offer more plausible explanations of the found characteristics of the Cathode rays as a form of electromagnetic waves.
Similarly, the introduced definitions of the electric charges and the magnetic flux as special categories of electromagnetic waves find plausible explanations to the “Kerr Effect” [9]. Such phenomena detect effects of electric and magnetic fields on the flow of electromagnetic waves. In case of electric fields, a quadratic electro-optic effect (QEO effect) is detected. In case of magnetic fields, a magneto-optic Kerr effect (MOK effect) is detected. The QEO effect is identified by a change in the refractive index of all materials when they are crossed by electromagnet waves in the presence of an applied AC or DC electric fields. Similarly; MOKE effect may be recognized, in some cases, by rotation of the plane of polarization of the transmitted light under the influence of magnetic field [9]. According to the introduced definitions, the light gains by the applied electric or magnetic fields the potentials differences ( ) or (
) or ( ), that converts the light waves into electric charges or magnetic flux of different index of refraction or rotated plane of polarization.
), that converts the light waves into electric charges or magnetic flux of different index of refraction or rotated plane of polarization.
Replacing the time axis by an entropy axis in the Maxwell’s solutions and considering the propagating EM waves as propagations of electric and magnetic energies of limited entropy production and energy quanta proves the description of photons as tiny bundle of electric and magnetic fields [18].
Introducing entropy, as a probability measure of disorder [18], to replace the time in Maxwell equations lead to a probabilistic Maxwell’s solution that is analogous to probabilistic wave solution Ψ(x, t) of the Schrodinger’s equation. The introduced fundamental equation can be valuable in studies that apply Poisson-NernstPlanck theory to investigate ion permeation and related transport processes [19].
Assigning a value of a definite electric potential for the charge, according to the stated definitions of electric charges, is similar to the assigned thermal potential, temperature, for the heat. Such electrical potential explains the phenomena of colored charges where each charge may have a different potential [8] and explain the phenomena of charging of clouds [12].
9. Conclusions
Reviewing experimentally and analytically the similarity and analogy between heat, electric charges and magnetic flux, the electric charge and magnetic flux were proved as special categories of energy or modified forms electromagnetic waves that have electrical or magnetic potentials. Previous analysis served also in expressing the magnetic flux and electric charges in terms of entropy change times a corresponding potential by analogy to heat flux. Introducing such postulates into the first law of thermodynamics led to a modified fundamental equation that embrace electric charge and magnetic flux as mechanisms of energy transfer. Considering time’s arrow as a property of entropy alone [7], the time in the Maxwell equation is replaced by entropy such that the areas bounded by the oscillating electrical and magnetic potentials represent the electrical and magnetic energies imparted by the electromagnetic wave. Such representation helps in expressing the qualities or potentials for the electric charge and the magnetic flux in analogy to the heat quality (temperature). The offered postulates lead to modified definitions of electric charge and magnetic flux in addition to plausible explanations of newly discovered phenomena in the fields of electromagnetism and thermodynamics as Kerr effect and magnetic expansion.