Evaluation and Improvement of Bed Load Formula Using Tapi River Data, India

S. M. Yadav, B. K. Samtani
DOI: 10.4236/jwarp.2010.23028                

Abstract

The effect of non uniformity of bed material on the sediment transport has been studied by various investi-gators in the past. In the present paper the bed load transport rate has been estimated for non uniform bed material considering the various variables like discharge, hydraulic mean depth, flow velocity, bed slope, average diameter of particle etc. by collecting field data of Tapi River. The majority of the bed load formulae represent a functional relationship between bed load discharge and shear stress. This study focuses on evalu-ating the bed load using Einstein’s formulae. The bed load of pre monsoon season is estimated using various field parameters. The mathematical model has been developed using effective shear stress and bed load dis-charge. The statistical analysis, multiple regression and curve fitting (by nonlinear square fitter) is carried out using allometric function of Micro cal Origin 7.5. The proposed model has been tested using five years field data of Tapi River other than that used for the development of model. The value of rmse is close to zero in-dicates a perfect fit between measured and predicted values. The inequality coefficient is close to 0.50 sug-gest moderate relationship between estimated and computed bed load.

Keywords

Sediment Transportation, Bed Load Equation, Einstein, Ripple Factor, Mathematical Model

1. Introduction

The subject of sediment transport and flow in alluvial streams are gaining importance with the increasing utilization of water resources. Einstein [1] has developed bed load equation as a function of sediment transport in the open channel flow, Bathurst et al. [2] proposed bed load discharge equations for steep mountain gravel bed rivers, Beschta [3] proposed conceptual models of sediment transport in streams, Emmett [4] studied bed load transport in two large, gravel-bed rivers, Idaho and Washington, Elliot et al. [5] studied the sediment transportation in Yampa river, North western Colorado, Gomez et al. [6]  assessed bed load transport formula for gravel bed rivers, Bravo–Espinosa [7] tested the bed load equations for 22 alluvial streams, Helmut et al. [8] evaluated and improved bed load discharge formulae for gravel bed rivers, Nian-Sheng Cheng [9] developed an exponential formula that does not involve the concept of the critical shear stress and Samtani [10] studied sediment transport characteristics of major rivers of South Gujarat, India. The majority of the bed load formulae represent a functional relation between bed load discharge and shear stress (Garde and Ranga Raju [11]). The formulae are characterized by three aspects:

1) The basic function q_b = A f (t₀-t_c).

2) The characteristic grain-size to be used.

3) The bed load correction factor.

The bed load transport formulae are site specific in nature and therefore can not be compared easily. In the present analysis the Einstein’s approach is used to find out the bed load transport for Tapi River, India. Using field data of Savkheda gauging station of Tapi River, Einstein’s bed load equation is evaluated and a new bed load equation is proposed which is tested using Tapi river data other than that used for the development of model. The main objectives of this paper are:    

1) Using various measured parameters determine q_b, t_{0 and} t_c.

2) To evaluate and propose modified bed load equation.

2. Study Area and Data Collection

Tapi is the second largest westward flowing river of peninsular India. The total length of the river is 724 km from origin to Arabian Sea. The Tapi basin is situated between latitudes 20' N to 22' N, 80% of the basin lies in Maharashtra and the balance in the state of Madhya Pradesh and Gujarat as shown in Figure 1. The Savkheda is one of the gauging station on the river Tapi. (Figure 2). Central Water Commission, Tapi Division, Surat is regularly collecting daily data of discharge and sediment at gauging site Savkheda on river Tapi. Savkheda is situated at a distance of about 488 kms from origin. The daily data during pre monsoon were collected for 15 years period from 1981 to 1995 [12]. Bed load data (seasonal) from 1981–95 [13] were collected for study. The validation of model is carried out using data of 2000-2005.

3. Discharge and Sediment Observations

Discharges were observed once in a day at 08:00 hours at all the sites and calculated by area-velocity methods. Cross-section is divided into 15 to 25 segments as per IS1192:1981. Depths were measured by sounding rods as per IS 3912: 1966. Necessary air and wet line corrections were done as per IS 1192: 1981. Velocity was measured by cup-type current meter as per IS 3910:1966. Suspended sediment samples were collected in Punjab Bottle Samplers at a depth of 0.6 D from the water surface.

4. Method of Analysis

The factor which is mainly responsible for the movement of the bed grains is the fluid drag. This drag force per unit of wetted area is called unit tractive force, and is given by  

t₀ = g RS (1)

where, t₀ is shear stress in kg/m², R is hydraulic radius in meters and S is bed slope. A certain minimum value of shear stress is required to move the grain, depending upon the internal friction of soil. The Einstein Brown equation follows semi theoretical approach based on fall velocity criteria. Einstein – Brown’s bed load transport equation is given by,

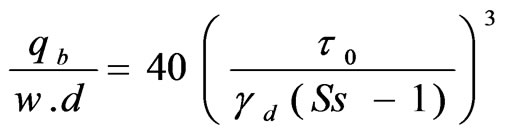(2)

Figure 1. Map of study area.

Figure 2. Digital image of study area showing Sarangkheda and Savkheda gauging station.

where, q_b = bed load transport rate weight per kg per meter width t₀ = average shear stress on channel boundary

γ_d = unit weight of sediments Ss = specific gravity of the stone or grain S = bed slope.

g = unit weight of fluid d = Mean diameter of stone or grain.

The functional relationship q_b = A f (t₀-t_c) can be approximated by an power function Y= a X ^b.

5. Computation of Bed Load and Related Parameters

From the observed and calculated daily data like discharge, area, velocity, wetted perimeter, hydraulic mean depth, Manning’s and Chezy’s constants, average diameter of sediment, mean diameter of sediment etc. are grouped under mainly five heads i.e., daily, monthly, pre monsoon, post-monsoon and yearly to facilitate the use of these data in analysis. In this paper analysis is carried out for pre monsoon season for Einstein’s approach. The equations stated above were used to find out bed load, shear stress and critical shear stress. The functional relationship is appropriated as following model:

Y= a X ^b(3)

Following steps has been followed to develop the model.

Step 1. The field daily data of 15 years has been converted in to monthly and seasonal data.

Step 2. Using the field data such as bed width, slope, hydraulic mean depth, discharge, velocity, temperature, mean diameter of particle the average and critical shear stress are computed.

Step 3. The Einstein’s equation is used to compute bed load transport in weight per unit width.

Step 4. The model Y = a X ^b is developed using 15 years of field data of Tapi river using Origin software 7.5.

Step 5. The model is tested using five years of data other than that used for model development.

Step 6. The testing of model is carried out by determining the statistical measures like root mean square error, inequality coefficient and discrepancy ratio.

The statistical analysis, multiple regression and curve fitting (by nonlinear square fitter) is using allometric function of Micro cal Origin 7.5.

 

6. Proposed Bed Load Formula

During pre monsoon, the estimated values of bed load

Figure 3. Relationship between effective shear stress and bed load transport rate.

Figure 4. Computed versus predicted bed load transport rates.

Table 1. Model validation.

discharge, shear stress and critical shear stress obtained using Einstein’s approach are plotted as shown in Figure 3. The stastical analysis is carried out using Micro cal Origin 7.5. The modified bed load equation is proposed as under:

Y = 0.20426*X ^0.98326

The value of coefficient comes out to be 0.20426 while value of index is 1.57634 with value of R² =0.98. The above equation may be used to calculate the correct bed load transported by Tapi River.

7. Model Validation

The above mathematical model is tested using five years of Tapi River data. The root mean square error (rmse) is one of the most convenient approaches for assessing simulation models. It measures the deviation between the trend of the predicted values and measured ones.

(4)

The value of rmse is zero indicates a perfect fit between measured and predicted values.

The discrepancy ratio is the measure of an equation to replicate data accurately. It is the ratio of a predicted to the measured bed load discharge. If this ratio is one, the equation exactly predicts the measured rate. If the ratio is less than one or greater than one the equation under or over predicts measured data respectively.

The inequality coefficient is a simulation statistics related to the rmse, defined as under,

(5)

The numerator is the root mean square error. If U=0 then q_bp = q_bo and there is a perfect fit. If U=1, then q_bp ≠ q_bo and the lacks predicative value. The value of root mean square error, Discrepancy coefficient and inequality coefficient for above model are presented in Table 1.

The value of rmse 0.027 is close to zero, discrepancy ratio is more than one and inequality ratio is close to zero which confirms the models moderate agreement. To examine more closely the accuracy of model, the computed bed load transport rates per unit channel width, q_computed  using field data are plotted in Figure 4 against the corresponding predicted values, q _predicted. In this figure the solid line represents the condition of perfect agreement.

8. Result Analysis

A new bed load transport relation for alluvial river has been proposed. The relation is an empirical fit to the data of Tapi river are considered to represent the two limits of the spectrum of bed load transport rate observed in the field and computed. The modified bed load equation based on Einstein’s bed load computation for Tapi River, pre monsoon season, Savkheda gauging station is as under.

Y = 0.20426 X 1.57634(6)

The value of coefficient obtained by above analysis is 0.20426 and the value of index is 1.57634. The above model is tested using five years field data of Tapi River. Bravo-Espinosa, M. [7] tested the bed load equations using 22 streams data. He used rmse, inequality ratio and discrepancy ratio to evaluate bed load equations. The rmse, inequality ratio and discrepancy ratio suggest good agreement between computed and predicted bed load. The increase in the channel discharge increase the rate of bed load transport but decreases the bed shear stress and increases critical shear stress responsible for the movement of bed particles. Helmut and Jonathan [8] derived form their study that Einstein formula is particularly appropriate for flood analysis. They concluded from their study that shear stress based formulae using single values for the threshold of motion do not perform well but shear stress formula modified on the basis of some measured data is improved considerably. In the present analysis the proposed bed load formula perform well for the Tapi river data.

9. Conclusions

Following findings can be summarized as conclusions:

• For Tapi River data the proposed bed load equation shows good agreement between estimated and computed bed load.

• Application of local hydraulics and sediment logic parameters improved formula prediction.

• The value of discrepancy ratio, which is a measure of an equation to replicate data accurately, is more than 2 which suggest moderate agreement between estimated and computed values of bed load.

• The value of rmse is close to zero indicates a perfect fit between estimated and computed values.

• In case of any other river across the globe, the proposed bed load equation gives considerable variation therefore the values of coefficient (a) and index (b) required to be modified to bring predicted and measured bed load in the close prediction band (Helmut and Jonathan).

10. Acknowledgement

It is to be acknowledging that without the permission given by Chief Engineer, Central Water Commission C.W.C., Narmada and Tapi River Basin Organization Baroda; this paper would not have seen the light of the day. The enormous assistance provided by the office of the Executive Engineer Central Water Commission (Tapi Division, C.W.C., Surat) during the preparation of this paper is duly acknowledged.

Notations       

        d   = sieve diameter of particle

          R  = hydraulic radius

         S   = bed slope

         q_bp   = predicted bed load transport in weight per unit width

         q_bo   = measured/computed bed load transport in weight per unit width

         U   = inequality coefficient

         q_b   = rate of bed load transport in weight per unit width

         t₀   = average shear stress on channel boundary

         t_c   = critical tractive stress

        a,b   = regression parameters

         ω   = fall velocity

         µ   = ripple factor

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	H. A. Einstein, “Formular for the transportation of bed load,” Transportation ASCE, Vol. 107, pp. 561–573, 1942.
[2]	J. C. Bathurst, W. H. Graf, and H. H. Cao “Bed load discharge equations for steep mountain rivers, Sediment transport in gravel Bed Rivers,” Wiley, U. K. Chichester, pp. 453–477, 1987.
[3]	R. L. Beschta “Conceptual models of sediment transport in streams, sediment transport in gravel-bed rivers,” C. R. Thorne, J. C. Bathurst, and R. D. Hey, eds., Wiley, U. K. Chichester, pp. 387–419, 1987.
[4]	W. W. Emmett “Bed load transport in two large, gravel- bed rivers,” Idaho and Washington Proceedings of 3rd Federal Inter-Agency Sedimentation Conference, Denver, Vol. 4, pp. 101–114, 1976.
[5]	J. G. Elliott, J. E. Kircher, and P. Von Guerard “Sediment transport in the lower Yampa River, northwestern Colorado,” US Geology Survey Water Resource Investigations Report, No. 84–4141, pp. 44, 1984.
[6]	B. Gomez and M. Church, “An assessment of bed loads sediment transport formulae for gravel Bed Rivers,” Water Resources Research, Vol. 25, No. 6, pp. 1161–1186, 1989.
[7]	M. Bravo-Espinosa, “Prediction of bed load discharges for alluvial channels,” PhD dissertation, University of Arizona, Tucson, Arizona, pp. 276, 1999.
[8]	M. H. Helmut and B. L. Jonathan, “Evaluation and improvement of bed load discharge formulas based on Helly –Smith sampling in an Alpine gravel bed rivers,” Journal of Hydraulic Engineering, Vol. 128, No. 5, pp 484–499, 2002.
[9]	N. S. Cheng, “Exponential formula for bed load transport, JHE, ASCE, Vol. 128, No. 10, October 2002.
[10]	B. K. Samtani, “Study of sediment transport characteristics with reference to major Rivers of South Gujarat,” Ph.D. Thesis, Faculty of Technology and Engineering, M. S. University of Baroda, India, 2002.
[11]	R. J. Garde and K. G. Ranga Raju, “Mechanics of sediment transportation and alluvial stream problems, Third ed., New Age Publication, New Delhi, 2006.
[12]	Central Water Commission (1980–1995), Water Resources Organization (NR), Integrated Water Year Book, Tapi Basin, Western River Circle, Nagpur, Tapi Division.
[13]	Central Water Commission (1980–1995), Bed Material Analysis Data, Western River Circle, Nagpur, Tapi Division.