1. Introduction
The set of primes represents a continuum, meaning that the difference between adjacent primes relative to the value of the prime (distance from the origin) approaches zero. In order to prove this prerequisite condition, the following steps starting with the density of the primes, their number and their distribution are shortly repeated, with references to more detailed evaluations.
1) First the approximation of the integral of the density by summation is shown. The error of this approximation is compensated by a recursive formula [1] .
2) The next step is the prime-number-formula and the proof, that this formula represents the low limit function of the number of primes, including the dispersion around the exact value, which is evaluated with the recursive formula, given by the complete-prime-number-formula. The standard deviation of the dispersion is proportional to the number of primes present up to the square root of the distance. The factor of proportionality is again an inherent property of the set of the primes.
3) The difference between the best estimate number of the primes over the distance and the corresponding value of the prime-number-formula is proportional to the square of the number of primes present up to the square root of the distance.
4) The dispersion of the number of primes around their best estimate value, relative to the error of the prime-number-formula is approaching zero. Therefore the prime-number-formula represents the low limit of the number of primes.
5) The double density of occupation of integral positions by the sets of multiples of the primes is introduced by reflecting the sets of the primes over a point at any distance [2] . The remaining free positions compos diads equidistantly placed primes to the point of reflection. For the sets of diads the above steps 1 to 4 are carried out. The number of equidistantly placed primes around any integer greater than two with an infinity growing low limit function proves Goldbach’s conjecture. Based on the symmetry of the set of diads it is proved, that at any distance within a section of the length equal to the square root of the distance there is at least one prime (see Annex 1).
2. The Number of Primes
De la Valée Poussin proved 1899 [3] , which the number of primes up to the distance (c) is given by the integral of the logarithmic density, which may be written as sum over all integers:
;
(2.1)
This above sum may be written as summing up first over all integers within the sections of the length (
) and then summing up over all the (
) sections of the length (
). Taking the average value over each section and summing up over the sections is a first simplification (see Annex 2), in the following used as sum over all sections:
(2.2)
The well proven prime-number-formula PNF results from a second simplification of the above approximation by taking for each of the sections the smallest value of the density at (
):
(2.3)
The difference between the sum over all sections of the number of primes and the value resulting from the PNF [2] , is proportional to (
), the square of the number of primes up to the distance (
):
(2.4)
because the value (
) quickly and asymptotically converges to a constant value:
(2.5)
Thus, the error of the second simplification resulting the PNF at the distance (c) is proportional to (
), the square of the number of primes present at (
). The factor of proportionality is evaluated in Annex 3 as (
):
The relation between the error of the PNF at (c) and the square of the number of primes up to (
) is invariant. The constant factor of proportionality (
) is an inherent propriety of the number of primes.
The systematic error of the PNF may be corrected by recursive application of a correction, resulting the complete-prime-number-Formula (CPNF) below, evaluated and demonstrated in ref [1] :
(2.6)
This formula converges very fast: Two steps with (
) are already sufficient.
The factor (
) is an inherent property of the set of primes.
Further, this formula gives identical results (see Annex 3) as (
):
;
(2.7)
The remaining error is the dispersion around the CPNF (see Annex 4). It is proportional to the number of primes up to (
), the series of multiples which are covering positions at (c):
;
(2.8)
Therefore, the dispersion of the effective number of primes around the CPNF relative to (
) is symmetrical around zero (with the factor of the standard deviation (
), as demonstrated in Annex 4. The error term is limited and approaches zero:
;
;
(2.9)
With (2.5) the difference between the best estimate number of primes CPNF and the PNF (the error of the PNF) is growing proportional to (
) while the width of the dispersion grows proportional to (
).
Therefore, the relation of the width of the dispersion to the error of the PNF is approaches zero with the distance (c) growing:
(2.10)
The fact that the error of the PNF relative to the PNF and herewith the dispersion around the CPNF are approaching zero with the distance indicates that the set of primes is approaching continuity with the distance:
(2.11)
3. The Number of Diads
Reflecting the series of multiples of any prime over a point at the distance (c) from the origin results the double density of occupation of integer positions within the interval (
) by the series of multiples of the primes if the prime is a relative prime to (c). This, because the positions covered by the straight and the reflected series of multiples are mutually exclusive for each prime if (c) is equal to a prime, greater than two. Reflected series of multiples of prime divisors of (c) do not change the occupation of integer positions: The number of remaining free integer positions has a minimum, if the point of reflection is a prime. This is demonstrated in Annex 5, Figure A4. The integer positions remaining free by the double density of occupation represent equidistant primes to the point of reflection, composing diads [2] . If any of the primes is a dividend of the distance of the point of reflection (c), then the reflected series of this specific prime does not cover additional positions: Therefore, the double density of occupation—with (c) as a prime—represents the minimum of positions left free by the double density of occupation.
The local density of free positions left by the density of occupation of the straight series of multiples of primes at the distance (
,
) is (
) and by the reflected series it is (
). The combined local density of free positions—the density of diads—is evaluated in [2] yielding with the constant (
). This constant has the double value of the twin prime constant (C2), defined by G. H. Hardy and John Littlewood [4] :
(3.1)
Similarly to the evaluation of the number of primes as simplification of the integral of the local logarithmic density of primes in (2.1), the best estimate of the local density of the diads results as simplification of the integral of the above density by taking the sum over all integers (This same generalization from the primes to the twins, respectively to the k-tuples was made already by G. H. Hardy and John Littlewood):
(3.2)
This function results the best estimate value of the number of diads CDNF see Annex 5. The dispersion of the effective number of diads around this function is symmetrical, there is no correction of this function required. The reason is the symmetry of the set of diads.
This above sum may be written as summing up first over all integers within the sections of the length (
) and then summing up over all the (
) sections, analogue to (2.2). Taking the average value over each section and—as a first simplification—summing over the sections gives the best estimate value of the number of diads:
(3.3)
Similarly, to the second simplification in case of the primes in (2.3), the low limit of the best estimate number of diads results—with the density taken for all sections of the length (
)—at the upper limit of the sections at (
) the diads-number-Formula (DNF):
(3.4)
dispersion is additive. Therefore, the dispersion in case of the double density of occupation is as well proportional to (
), the number of primes covering positions at the distance (c).
;
(3.5)
Therefore, the standard deviation f the relative dispersion of the diads approaches a constant value, similarly to the standard deviation of the dispersion of the effective number of the primes around the CPNF:
(3.6)
The difference between the number of diads CDNF (3.2) and the value resulting from the DNF is proportional to (
), the square of the number of primes up to the distance (
) on the power (y,
). The factor of proportionality (
) quickly and asymptotically converges with (
) to a constant value (
), as shown in Annex 6.
(3.7)
On the other hand, the low limit of the difference between the best estimate value and the low limit of the number of diads may be written as follows:
(3.8)
Resulting the low limit as:
(3.9)
Herewith the difference between the CDNF and the DNF—the error of the DNF—is growing proportional to (
,
) while the width of the dispersion around the CDNF grows proportional to (
).
Therefore, the relation of the width of the dispersion around the CDNF to the error of the DNF is approaching zero with the distance (c) growing:
(3.10)
The fact, that the dispersion of the effective number of diads around the CDNF relative to the DNF approaches zero with the distance indicates, that the set of diads is approaching continuity:
(3.11)
Therefore, the DNF represents for each integer greater then two a monotonously to infinity growing low limit function. It is defined for primes as point of reflection of the double density of occupation by the series of multiples of primes. If the point of reflection is not a prime, the dividends of the distance up to the point of reflection cover no additional integer positions, then in case of the single density of occupation and the number of the remaining free positions (diads) remain larger. This is the case as well for even numbers as points of reflection, proving Goldbach’s conjecture.
The best estimate values of the diads, given by the approximating functions, the dispersion of the effective values around the best estimate values and the low limit functions are evaluated with the same method. Because the PNF is well proven for the set of the primes, the DNF and the other results for the diads are proven on the same right.
Diads with the central prime of reflection compose triads, the triads-number-formula TNF is with the density of primes therefore (
).
Reflecting the union of the series of multiples of the primes additionally over the primes at both ails of the triads gives the set of five equidistant primes, the pentids. The number of the pentids , the pentides-number-formula PENF is (
).
All formula for the number of the remaining free positions in case symmetric coverage of the set of integer positions—like (3.3)—do not require any correction, like the number the of primes (2.2) to (2.6). The origin of the required correction is therefore the asymmetry of the sets of primes.
4. The Continuity of the Set of Primes as Variable
Comparing the sets of primes and diads, the following similarities are obvious:
With (2.5) the difference between the best estimate number of primes CPNF and the PNF is proportional to (
), the square of the number of primes up to (
).
Similarly, with (3.7) the difference between the best estimate number of diads CDNF and the CDNF is proportional to (
), the square of the number of primes up to (
).
With (2.4) and (3.8) the factors of proportionality (
) and (
) are similar.
With (2.10) and (3.9) the dispersion around the effective numbers of primes, respectively diads are approaching zero, when compared with the differences between CPNF and PNF, respectively between CDNF and DNF, therefore the low limit functions are effectively low limit functions.
Now comes an important point: Taking the best estimate numbers of the diads in (3.3) in the first section from zero to (
), the number of free positions composing diads is:
(4.1)
Taking the sum of the diads over the first sections up to (
) does not influence the validity of the properties of the set of the diads: everything valid for the whole set of diads up to the distance (c) remains valid for the subinterval up to the distance (
). This fact is demonstrated in Annex 7.
Because of symmetry over (c), in case of the double density of occupation, the same amount of diads is present within the last section from (
) to (
), (the same length) and their number is growing to infinity as well:
;
(4.2)
If in case of the double density of occupation at (
) the number of free positions within the last section of the length (
) is rising without limit to infinity, then this is certainly the case as well within the larger distance for the last section of the length (
) and even more in case of the single density of occupation.
The same is the case within the section of the length (
) following (
) and therefore within the section of the length (
) following (
) as well. This, because the first free position covered by the series of multiples of the smallest possible prime greater than (
), equal to (
) is already greater than (
).
This smallest prime must be (
) in case (
) and (
) are twins. In this case (
) and the square of this smallest possible prime is already over (
):
(4.3)
Herewith the low limit of free positions left within the section of the size (
) following (c) is not smaller, than the number of free positions within the last section of the same size just below (c).
It follows, that the set of the primes up to (
) normed with this last prime represent, as limit, a continuum, since for any prime within the set the following limit is valid:
;
(4.4)
herewith:
The knowledge of the function of the best estimate value of the number of the primes allows for the evaluation of the standard deviation of the effective number of the primes around the exact function, given in ref [2] . From the constancy of the relative value of the standard deviation follows the integrability on the inverse of the primes.
5. Conclusions
The reflection of the set of the union of the series of multiples of the primes over any position equal to an integer greater than two leaves positions of integers free, which compose subsets of the primes. This subset up to the point of reflection has similar properties to the primes. Its symmetry around the point of reflection allows it to prove Goldbach’s conjecture and the continuity of the set of primes.
The number of sets of primes with distances of any even integer between its primes is similarly unlimited. All these sets have the best-estimated number of primes with the dispersion of the effective numbers around these best-estimated functions. All these sets have low limit functions of their number of primes. The distance between the best estimate function and the low limit function grows to infinity and remains always infinitely larger than the dispersion. Therefore, all of these sets compose continuums within the set of integers.
Annexes
Annex 1: Definition of Vectors and Variables for the Numeric Evaluation
First some general functions and values are defined: Based on the requirement of the constrain of non-divisibility by all smaller primes, a set of consecutive primes is evaluated and written to a file.
From this file they are read: (
). The number of the primes in the set and their numbering are: (
,
).
The complete-prime-number-formula CPNF, (2.6) is evaluated with the following routine (floor and ceil stand for round down and round up):
;
;
(A1.1)

For the evaluation of the number of the next smaller prime to the distance (c) the routine resulting the index (
) of the prime next to any integer is needed (
). The evaluation starts either at the last evaluated index (
), or at the index resulting from the complete-prime-number-Formula (see A1.1 and ref. [2] ). This shortens the evaluation process. In case (
) is greater than the distance, the index is lowered. In case it is smaller, the index is risen until the corresponding prime is just smaller, or equal to the distance:

 (A1.2)
(A1.2)
Further functions are the formula evaluating the index of the next smaller prime to any distance and to the square root of any distance:
;
;
;
(A1.3)
For the visualization of the results of the analysis the functions will be taken at sparse values, at distances corresponding to multiples of the square root of the largest prime considered. The index (kk) of the sparse values for the diads is limited to half the number of the index (k) in case of the primes:
;
;
;
(A1.4)
;
;
The vectors of the indexes of the primes next smaller to these sparse distances (
), respectively to their square roots (
) are evaluated as (
), respectively as (
). They are evaluated once and written to files. They are read from these files:
;
(A1.5)
;
Annex 2: Evaluation of the Number of Primes as Sum over Sections and of the Factor of Correction of the Sum over All Sections
The number of primes as sum over sections is evaluated with (2.2) as a first simplification:
(A2.1)
The approximating function is evaluated at sparse distances, respectively at the next smaller prime to these distances (
) with (2.2). The evaluation at the next smaller prime corresponding to each distance assures, that the evaluated numbers of the primes correspond exactly to the distances considered:
(A2.2)
They are evaluated once and written to a file. They are read from this file:
The result of the first simplification (2.2) giving the sum over the sections of the density of primes has an error. This error is proportional to the number of primes up to (
). The error relative to (
) results the factor of correction. Assuming the factor of correction (
) is constant over the distance (c), it may be evaluated as relation of the average error to the effective number of primes (
). The average error is:
;
(A2.3)
The value of the factor of correction is herewith:
;
;
(A2.4)
Figure A1 shows the independence of the factor of correction (
) from the distance. The averaging process (A2.3) to evaluate the factor of correction is therefore justified. This factor (
) is invariant, an inherent property of the prime numbers. It is important because it is applied in the recursive Formula (2.6) of the complete-prime-number-formula CPNF.
![]()
Figure A1. Convergence of the relation of the average relative error of the sum over all sections.
Annex 3: Evaluation of the CPNF and the Error of the Second Simplification
The results of the CPNF, (2.6) are evaluated with (A1.1) once at sparse values of the distance (
). They are written to a file and are read from this file:
(A3.1)
;
The number of primes resulting from the second simplification (2.3) results the PNF. The difference between the CPNF and the PNF results the error of the PNF. At the instance (c) it is proportional to (
), the square of the number of primes covering positions at the distance (
). The factor of the proportionality (
) is illustrated in Figure A2 below:
![]()
Figure A2. Relation of the difference between the best estimate number of primes (CPNF) and its value evaluated with the prime-number-Formula (PNF) to (
).
;
(A3.2)
;
;
Annex 4: Dispersion of the Effective Number of Primes around the CPNF
The standard deviation SD of the relative dispersion of the primes around their best approximation (2.8) is evaluated as follows:
;
(A4.1)
The results are evaluated once and written to a file, and they are read from this file:
;
The average of the relation of the standard deviation converges to a final value, to the factor of proportionality (
). This factor is evaluated as follows:
(A4.2)
The results are evaluated once and written to a file. They are read from this file:
The constant factor is equal to the final average value of the standard deviation at large distances. The Figure A3 illustrates that the standard deviation is about constant over the distance. This fact rectifies taking the average over the whole distance for the evaluation:
![]()
Figure A3. Dispersion of the standard deviation of the dispersion of the number of primes around its average, the resulting constant value (
).
;
(A4.3)
Figure A3 indicates that the standard deviation of the dispersion of the effective number of primes around its approximation is rising proportionally to (
), the number of the series of multiples of primes, which are covering integer positions at this distance (c). The factor of proportionality (
) is again an inherent property of the prime numbers.
Annex 5: The Effective Number of Diads and Their Approximation
The approximate values of the number of diads (3.3) are evaluated once for sparse distances (
), with the center of the diads being equal to the next smaller prime to the sparse distances. The results are written to a file and are read from this file:
(A5.1)
;
Similarly, the total number of diads around the center point at (c) with components within the first section up to (
) is given by (4.1). The results are written to a file and are read from this file:
;
(A5.2)
The routine evaluating the effective number of diads at (c) checks for each prime (
), if the integer at de distance (
) were a prime too. If it is a prime, then the sum of the diads around the central point is risen by one. The checking is made by control of the equality of the prime next to the distance (d) to the distance itself. Similarly, the diads within the first section are evaluated. For the evaluation of the index of the next smaller prime to a given distance the routine (A1.2) is used:

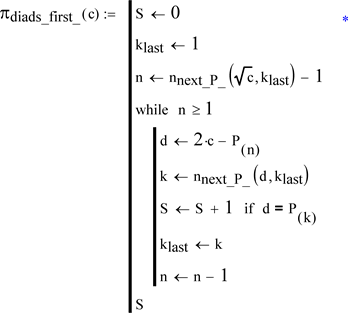 (A5.3)
(A5.3)
The number of diads is evaluated for points of reflection being primes at sparse distances. The evaluation is carried out as sum of all diads up to the points of reflection (
) and for diads within the first section up to the square root of the distance of the point of reflection (
). Further as well for the case if the points of reflection are not primes, but even numbers (
) just next below the primes at sparse distances (
), with variable numbers of prime divisors. The comparison of the number of diads in case of the point of reflection is a prime or the next smaller integer to the prime is demonstrated in Figure A4. Because the evaluation is time consuming, the results are written to files and read from these files:
![]()
Figure A4. Comparison of the number of diads evaluated for points of reflection being primes with diads evaluated for even numbers just below the same primes.
;
;
Annex 6: Evaluation of the Error of the Second Simplification of the Diads
The number of diads resulting from the second simplification (3.3) results the DNF. The difference between the CDNF, (3.2) and the DNF, (3.9) results the error of the DNF. At the distance (c) it is proportional to (
), the number of primes covering positions at the distance (c). The difference between the CDNF and the DNF is:
;
(A6.1)
The factor of the proportionality (
) results with the relation of the difference between the CDNF and the DNF to (
,
) taken as average over the spare distances, illustrated in Figure A5. For the approximation of the diads in the first section an additional factor of (1.15) is applied: The reason is, that in this case there are no subsections over the first section considered.
![]()
Figure A5. Relation of the difference between the CDNF and the DNF to (
).
;
(A6.2)
Annex 7: Evaluation of the Properties of the Dispersion of Diads
The dispersion of both, of the free positions left by both, by the straight and by the reflected series of multiples of primes are proportional to the number of primes (
), the series of multiples of primes which are covering free positions at (c). Therefore, this is the case by the dispersion of the number of diads around its best estimate approximation as well. The relative dispersion with reference to (
) is evaluated and shown in the Figure A6. The results are written to a file and read from this file:
![]()
Figure A6. The dispersion of the relative number of diads around its best estimate approximation (left) and the standard deviation of the dispersion (right).
;
(A7.1)
The width of the dispersion of the diads is therefore estimated as
,
(A7.2)
The standard deviation SD of the dispersion (A7.1) is assumed to be constant for large distances. It is evaluated as:
(A7.3)
The factor of proportionality for the standard deviation of the diads is:
(A7.4)
Figure A6 indicates that the standard deviation of the dispersion of the effective number of diads around its approximation is rising proportionally to (
), the number of the series of multiples of primes, which are covering integer positions at the distance (c). The factor of proportionality (
) is again an inherent property of the prime numbers.