TULLY-FISHER Law Demonstrated by General Relativity and Dark Matter ()

1. Introduction
One of the most important scaling laws is the empirical Tully-Fisher relation [1] , between the stellar mass or luminosity of a galaxy and its rotation velocity v. The stellar Tully-Fisher is a power law
with α ~ 4 - 5 depending on the method used to estimate stellar masses [2] [3] and depending on how the rotation velocities are defined [4] [5] . When the baryonic mass Mb (stars + cold gas) is used instead of the stellar mass, the baryonic Tully-Fisher relation [6] becomes an extremely tight power law
, with α ~ 4 [5] [7] [8] .
In our study, we are going to demonstrate the Tully-Fisher law with the solution of DM explained without exotic matter but with a uniform gravitic field (the 2nd component of GR similar to the magnetic field in EM) as proposed by the author [9] . This field would be generated by galaxy clusters [10] and would embed large areas of the Universe (and then the galaxies) explaining this excess of gravitation misnamed, in this explanation, DM. We will first remind you how Linearized General Relativity (LGR) is obtained from GR, how LGR equations can explain DM and the expected values of the uniform gravitic field required to explain DM component. We will secondly verify that the measured coefficients of the Tully-Fisher law
allow retrieving the expected gravitic field explaining the DM. Third, the main goal of this study, we will demonstrate the expression of Tully-Fisher law in our explanation of DM, making this theoretical DM explanation extremely consistent with the observations.
2. Dark Matter Explained by General Relativity
2.1. From General Relativity to Linearized General Relativity
From GR, one deduces the LGR in the approximation of a quasi-flat Minkowski space (
;
). With the following Lorentz gauge, it gives the following field equations as in [11] (with
and
):
(1)
with:
(2)
The general solution of these equations is:
(3)
In the approximation of a source with low speed, one has:
(4)
And for a stationary solution, one has:
(5)
At this step, by proximity with electromagnetism, one traditionally defines a scalar potential
and a vector potential
. There are in the literature several definitions as in [12] for the vector potential
. In our study, we are going to define:
(6)
with gravitational scalar potential
and gravitational vector potential
:
(7)
with K (determined in [9] ) a new constant defined by:
(8)
This definition is
very small compared to G.
The field Equations (1) can be then written (Poisson equations):
(9)
with the following definitions of
(gravity field) and
(gravitic field), those relations can be obtained from the following equations (also called gravitomagnetism) with the differential operators “
”, “
” and “
”:
(10)
with the Equations (2), one has:
(11)
The equations of geodesics in the linear approximation give:
(12)
It then leads to the movement equations:
(13)
Remark: All previous relations can be retrieved starting with the parameterized post-Newtonian (PPN) formalism and with the traditional gravitomagnetic field
. From [13] one has:
(14)
The traditional gravitomagnetic field and its acceleration contribution are:
(15)
And in the case of GR (that is our case):
(16)
It then gives:
(17)
And with our definition:
(18)
One then has:
(19)
with the following definition of gravitic field:
(20)
One then retrieves our previous relations:
(21)
The interest of our notation (
instead of
) is that the field equations are strictly equivalent to Maxwell’s idealization, in particular, the speed of the gravitational wave obtained from these equations is the light celerity
just like in EM
. Only the movement equations are different with the factor “4”. But of course, all the results of our study can be obtained in the traditional notation of gravitomagnetism with the relation
.
2.2. From Linearized General Relativity to DM
In the classical approximation (
), the linearized general relativity gives the following movement equations from (13) with
the inertial mass and
the gravitational mass:
(22)
The traditional computation of rotation speeds of galaxies consists of obtaining the force equilibrium from the three following components: the disk, the bugle, and the halo of dark matter. More precisely, one has [14] :
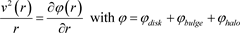 (23)
(23)
Then the total speed squared can be written as the sum of squares of each of the three-speed components:
 (24)
(24)
Disk and bulge components are obtained from gravity field. They are not modified in our solution. So, our goal is now to obtain only the traditional dark matter halo component from the linearized general relativity. According to this idealization, the force due to the gravitic field  takes the following form
takes the following form 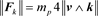 and it corresponds to previous term
and it corresponds to previous term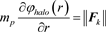 . As explained in [9] , the natural evolution to the equilibrium state justifies that one assumes the approximation
. As explained in [9] , the natural evolution to the equilibrium state justifies that one assumes the approximation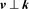 . This assumption is important because it leads to several important predictions. In particular, the motion of dwarf satellite galaxies of a host should be roughly in a plane (
. This assumption is important because it leads to several important predictions. In particular, the motion of dwarf satellite galaxies of a host should be roughly in a plane ( ). It then gives the following equation:
). It then gives the following equation:
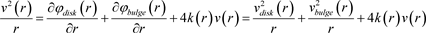 (25)
(25)
Our idealization means that:
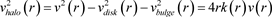 (26)
(26)
The equation of dark matter (gravitic field in our explanation) is then:
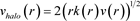 (27)
(27)
This equation gives us the curve of rotation speeds of the galaxies as we wanted. Because we know the curves of speeds that one wishes to have for DM component, one can then deduce the curve of the gravitic field  inside the galaxy:
inside the galaxy:
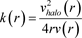 (28)
(28)
2.3. Dark Matter as the 2nd Component of the Gravitational Field 
This solution of DM as the gravitic field has been studied in [9] for 16 galaxies (Table 1). It shows that this solution is mathematically possible but with two physical mandatory unexpected behavior for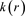 . First, the curve of the gravitic field
. First, the curve of the gravitic field 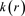 becomes necessarily flat at the end of the galaxies. For such a field (similar mathematically to a magnetic field in EM) it is only possible if the galaxies are immersed in a uniform gravitic field
becomes necessarily flat at the end of the galaxies. For such a field (similar mathematically to a magnetic field in EM) it is only possible if the galaxies are immersed in a uniform gravitic field . Second, the value of this field for these 16 galaxies is in the interval:
. Second, the value of this field for these 16 galaxies is in the interval:
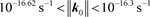 (29)
(29)
From these data (Table 1), one can deduce a mean value of 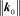 and a mean value of
and a mean value of![]() :
:
![]() (30)
(30)
The position ![]() is the position where the gravitic component of the galaxy becomes negligible compared to the external uniform gravitic term explaining DM. It roughly represents the beginning of the flat part of the rotation speed curve of the galaxies. We will use these two values at the end of the article in the demonstration of the Tully-Fisher law.
is the position where the gravitic component of the galaxy becomes negligible compared to the external uniform gravitic term explaining DM. It roughly represents the beginning of the flat part of the rotation speed curve of the galaxies. We will use these two values at the end of the article in the demonstration of the Tully-Fisher law.
![]()
Table 1. Distance r0 to the center of the galaxy where the internal gravitic field ![]() generated by the galaxy becomes equivalent to the external gravitic field k0 generated by the galaxies’ cluster. k0 dominates for
generated by the galaxy becomes equivalent to the external gravitic field k0 generated by the galaxies’ cluster. k0 dominates for![]() .
.
3. TULLY-FISHER Law Obtained from a Uniform Gravitic Filed ![]() of LGR
of LGR
We will first verify that this theoretical solution of DM is consistent with the Tully-Fisher law by retrieving our value of DM ![]() from the coefficient of the law which has been experimentally observed. And secondly, we will demonstrate how
from the coefficient of the law which has been experimentally observed. And secondly, we will demonstrate how ![]() and LGR can obtain the Tully-Fisher law.
and LGR can obtain the Tully-Fisher law.
Let’s note ![]() the Newtonian rotational speed and
the Newtonian rotational speed and ![]() the Newtonian rotational speed plus the halo DM component, (25) can be written:
the Newtonian rotational speed plus the halo DM component, (25) can be written:
![]() (31)
(31)
And more explicitly with M the galaxy’s mass:
![]() (32)
(32)
which gives:
![]() (33)
(33)
3.1. From the TULLY-FISHER Law to the Uniform Gravitic Field ![]() of LGR
of LGR
The Tully-Fisher law is written ![]() and can be rewritten
and can be rewritten ![]() . Several couples
. Several couples ![]() can be obtained experimentally for this law [15] depending on the masses considered and the methods of obtaining the characteristic speed of rotation as previously said.
can be obtained experimentally for this law [15] depending on the masses considered and the methods of obtaining the characteristic speed of rotation as previously said.
Let’s rewrite our expression (33):
![]() (34)
(34)
which gives:
![]() (35)
(35)
In order to get an expression that looks like the Tully-Fisher law, we are going to use the following approximation for large r (in the flat part of the rotation speed curve):
![]() (36)
(36)
Furthermore, in our explanation of DM, ![]() is a uniform field, i.e.
is a uniform field, i.e.![]() . By replacing the occurrence of
. By replacing the occurrence of ![]() in the brackets, one has:
in the brackets, one has:
![]() (37)
(37)
If one has:
![]() (38)
(38)
The expression becomes:
![]() (39)
(39)
And finally:
![]() (40)
(40)
The couples ![]() of
of ![]() are in general given for a graph whose velocities are in km·s−1 and the masses in solar mass (
are in general given for a graph whose velocities are in km·s−1 and the masses in solar mass (![]() ). One can then rewrite with
). One can then rewrite with ![]() and
and![]() :
:
![]() (41)
(41)
We want to verify that the values of ![]() form the Tully-Fisher law allow retrieving the values of the gravitic field
form the Tully-Fisher law allow retrieving the values of the gravitic field ![]() explaining the DM to ensure that our theoretical solution is consistent with the Tully-Fisher law. For that, let’s rewrite:
explaining the DM to ensure that our theoretical solution is consistent with the Tully-Fisher law. For that, let’s rewrite:
![]() (42)
(42)
For these calculations, one will use:
![]() (43)
(43)
This value of r justify the previous approximation (36)
In [2] the observations give the following couple:
![]() :
:
![]() (44)
(44)
In [15] , one has the 4 following couples:
![]() :
:
![]() (45)
(45)
![]() :
:
![]() (46)
(46)
![]() :
:
![]() (47)
(47)
![]() :
:
![]() (48)
(48)
Let’s verify the previous approximation (38) with the smallest value of![]() :
:
![]() (49)
(49)
These calculations show that the expected values of ![]() to explain DM without exotic material (
to explain DM without exotic material (![]() ) are consistent with the Tully-Fisher law. We will now go further by proving this law within the framework of the LGR and our explanation of DM.
) are consistent with the Tully-Fisher law. We will now go further by proving this law within the framework of the LGR and our explanation of DM.
3.2. From the Uniform Gravitic Field ![]() of LGR to the TULLY-FISHER Law
of LGR to the TULLY-FISHER Law
As we noticed in the previous paragraph, in our relation, there is the parameter position r which appears while the Tully-Fisher relation does not explicitly depend on it. To no longer explicitly depend on this parameter, we need to define a procedure to determine a characteristic position r. It should be noted that we are in the same situation for the TULLY-FISHER law to define the characteristic speed of rotation to be considered. Several methods are used [5] and the mean velocity along the flat part of the rotation curve seems to minimize the scatter of the relation [4] . The question in our context is somehow to find which method was adopted to define the characteristic position r corresponding to the characteristic velocity on the curve of the rotational velocities of the galaxies. This characteristic speed is linked to the flat zone of the speed curve, the characteristic position will certainly be a characteristic position in this zone. We can imagine 2 simple methods.
A 1st would consist of finding the position of the beginning of the flat zone ![]() then placing the cursor at a fixed relative position,
then placing the cursor at a fixed relative position, ![]() with respect to the beginning of this zone,
with respect to the beginning of this zone, ![]() and finally determining the value of
and finally determining the value of![]() . We will see what it will be
. We will see what it will be![]() . This method makes it possible to find punctually the good values for the law of Tully-Fisher but it doesn’t give the good slope of the law.
. This method makes it possible to find punctually the good values for the law of Tully-Fisher but it doesn’t give the good slope of the law.
A 2nd method would consist of finding a threshold for the value of the gravitational forces ![]() from which the gravitational forces are sufficiently weak so that the influence of the DM dominates (a priori in the flat part of the curve). This method allows for demonstrating the Tully-Fisher law, values, and slope. But certainly, also the extent of the area to which this law is applicable.
from which the gravitational forces are sufficiently weak so that the influence of the DM dominates (a priori in the flat part of the curve). This method allows for demonstrating the Tully-Fisher law, values, and slope. But certainly, also the extent of the area to which this law is applicable.
3.2.1. 1st Method to Demonstrate the Tully-Fisher Law
The beginning of the flat zone of the rotational speed curve ![]() corresponds approximately to the place where the intensity of the Newtonian force is of the same order as the component of DM:
corresponds approximately to the place where the intensity of the Newtonian force is of the same order as the component of DM:
![]() (50)
(50)
We then write (to be somewhere in the flat zone):
![]() (51)
(51)
Our relation (32) gives:
![]() (52)
(52)
![]() (53)
(53)
![]() (54)
(54)
![]() (55)
(55)
![]() (56)
(56)
![]() (57)
(57)
with ![]() and
and ![]() (red curve in Figure 1) one obtains a curve that is very close to the Tully-Fisher law, passing through the cloud of expected measured points. But the slope of the curve is unsatisfactory. This 1st method informs us that the position
(red curve in Figure 1) one obtains a curve that is very close to the Tully-Fisher law, passing through the cloud of expected measured points. But the slope of the curve is unsatisfactory. This 1st method informs us that the position ![]() of the beginning of the flat zone is certainly a good order of magnitude for the definition of the position associated with the measurement of the speed of rotation for the law of Tully-Fisher. Even if this result is not completely satisfactory, it is very encouraging. With this information, we will now improve our result with the 2nd method.
of the beginning of the flat zone is certainly a good order of magnitude for the definition of the position associated with the measurement of the speed of rotation for the law of Tully-Fisher. Even if this result is not completely satisfactory, it is very encouraging. With this information, we will now improve our result with the 2nd method.
3.2.2. 2nd Method to Demonstrate the Tully-Fisher Law
Let’s define a threshold value of the intensity of the force for which, we hope to find the position on the rotation curve corresponding to the characteristic speed considered for the Tully-Fisher law:
![]() (58)
(58)
![]()
Figure 1. The red curve representing our relation obtained from our 1st method is superposed on graph from [15] .
This position is denoted ![]() because we have seen previously that it was most certainly the beginning of the flat zone. The following calculation will confirm this result. One can then rewrite our relation to LGR:
because we have seen previously that it was most certainly the beginning of the flat zone. The following calculation will confirm this result. One can then rewrite our relation to LGR:
![]() (59)
(59)
![]() (60)
(60)
![]() (61)
(61)
![]() (62)
(62)
![]() (63)
(63)
![]() (64)
(64)
![]() (65)
(65)
![]() (66)
(66)
![]() (67)
(67)
We then obtain our expression of Tully-Fisher law (red curve in Figure 2):
![]() (68)
(68)
An approximation of this relation in the form “![]() ” could be obtained and would lead to an analysis equivalent to what we have studied in the previous sections, but the more accurate relation between M and v in our explanation is the latter. And the result is impressive as one can see in Figure 2. Furthermore, the obtention
” could be obtained and would lead to an analysis equivalent to what we have studied in the previous sections, but the more accurate relation between M and v in our explanation is the latter. And the result is impressive as one can see in Figure 2. Furthermore, the obtention ![]() is consistent with our definition of DM, as we are now going to see it.
is consistent with our definition of DM, as we are now going to see it.
As calculated previously, if we take the average of the beginnings of the flat zones and the mean of the values of the gravitic field explaining DM (30) and by taking the characteristic mass previously used for our calculations (43), one has:
![]() (69)
(69)
![]()
Figure 2. The red curve representing our relation obtained from our 2nd method is superposed on the graph from [15] .
For this value of mass, on the graphs (Figure 1 and Figure 2) the corresponding characteristic rotational speed is around:
![]() (70)
(70)
All these characteristic values allow defining our characteristic force threshold:
![]() (71)
(71)
The red curve in Figure 2 representing the relation (68) is obtained with ![]() and
and![]() .
.
This time, compared to the 1st method, not only does the curve pass well through the cloud of measured points, but the slope of the curve is also excellent. Add to this that the characteristic value of ![]() is also not only in the right order of magnitude but this time in the interval required to explain the DM.
is also not only in the right order of magnitude but this time in the interval required to explain the DM.
4. Discussion
In the same way that there are several methods for defining the characteristic velocity used in the Tully-Fisher law giving more or less tight values of its coefficients, the role of ![]() provides a method for obtaining this characteristic velocity. Indeed, finally
provides a method for obtaining this characteristic velocity. Indeed, finally ![]() implies
implies![]() . The rotation speed of the galaxy to be considered will be that at the intersection of this curve with its rotation speed curve.
. The rotation speed of the galaxy to be considered will be that at the intersection of this curve with its rotation speed curve.
The fact of obtaining a value of ![]() from the explanation of the DM (i.e. by the expression of the uniform gravitic field of the LGR, “
from the explanation of the DM (i.e. by the expression of the uniform gravitic field of the LGR, “![]() ” and by the values of this field “
” and by the values of this field “![]() ”) and which accounts for the Tully-Fisher law is undeniably an extremely strong point which validates this explanation of the DM (without exotic matter and in agreement with the RG). One can remind that this solution predicts the existence of planes of corotating satellite galaxies [16] and that in the WLM’s dwarf galaxy case, these expected values of field
”) and which accounts for the Tully-Fisher law is undeniably an extremely strong point which validates this explanation of the DM (without exotic matter and in agreement with the RG). One can remind that this solution predicts the existence of planes of corotating satellite galaxies [16] and that in the WLM’s dwarf galaxy case, these expected values of field ![]() can retrieve the density of the gaseous intergalactic medium and interstellar gaseous medium [17] .
can retrieve the density of the gaseous intergalactic medium and interstellar gaseous medium [17] .
Another point seems important. The Tully-Fisher law in its form “![]() ” has no maximum limit. It gives no justification for not continuing beyond
” has no maximum limit. It gives no justification for not continuing beyond![]() . Our relationship necessarily indicates a break from a certain maximum value of the mass of the galaxy (bending of the curve). This relationship thus provides a justification for the fact that galaxies can have a maximum mass value which with our approximate study gives
. Our relationship necessarily indicates a break from a certain maximum value of the mass of the galaxy (bending of the curve). This relationship thus provides a justification for the fact that galaxies can have a maximum mass value which with our approximate study gives ![]() in agreement with observations.
in agreement with observations.
5. Conclusion
In this study, we show that the explanation of dark matter in the form of a uniform gravitic field ![]() (the 2nd component of GR similar to the magnetic field in EM giving the Lense-Thirring effect) makes it possible to obtain the Tully-Fisher law. Obtaining this law is based on two important characteristics of this solution, one theoretical, namely the shape of this field, “
(the 2nd component of GR similar to the magnetic field in EM giving the Lense-Thirring effect) makes it possible to obtain the Tully-Fisher law. Obtaining this law is based on two important characteristics of this solution, one theoretical, namely the shape of this field, “![]() ”, defined by the LGR, and the other practical, namely the values required to obtain the component of DM “
”, defined by the LGR, and the other practical, namely the values required to obtain the component of DM “![]() ”. Thus, obtaining the Tully-Fisher law is undeniably linked to the validity of this solution. This demonstration reinforces this solution of the DM which is also extremely economical in hypothesis if we compare it to MOND (which calls into question the theoretical framework of gravitation) or to the existence of an exotic matter (with a new behavior and still not found).
”. Thus, obtaining the Tully-Fisher law is undeniably linked to the validity of this solution. This demonstration reinforces this solution of the DM which is also extremely economical in hypothesis if we compare it to MOND (which calls into question the theoretical framework of gravitation) or to the existence of an exotic matter (with a new behavior and still not found).
In addition to providing the correct values (passing through the measured points) and the correct slope of the Tully-Fisher law, this relationship goes further by showing a systematic break in the curve for mass values roughly around![]() . This new relationship thus provides a justification for the existence of a maximum mass for galaxies.
. This new relationship thus provides a justification for the existence of a maximum mass for galaxies.
This study finally leads to 3 major results, the demonstration of the Tully-Fisher law, a justification of a maximal mass of the galaxies but perhaps even more important a validation of the explanation of the DM in the form of a uniform gravitic field embedding the galaxies.