Joint Power Control and Spectrum Allocation for Cognitive Radio with QoS Constraint ()
1. Introduction
The spectrum of the wireless networks is generally regulated by governments via a fixed spectrum assignment policy. However, in recent years, the demand for wireless spectrum use has been growing dramatically with the rapid development of the telecommunication industry, which has caused scarcity in the available spectrum bands. Furthermore, the underutilization of the licensed spectrum bands makes the situation even worse [1]. Cognitive radio [2], with the ability to sense unused bands and adjust transmission parameters accordingly, is an excellent candidate for improving spectrum utilization. In cognitive radio networks, the cognitive (unlicensed) user needs to detect the presence of the primary (licensed) users as quickly as possible and dynamically changes the system parameters, such as transmit power level, so as to best utilize the valuable spectrum [3].
There are two kinds of spectrum sharing method: spectrum overlay and spectrum underlay. The researches of underlay spectrum limit the transmit power of the cognitive users and make sure that the interference temperature does not exceed certain threshold [4]. The related works on spectrum sharing schemes under interference temperature mainly include [5–7]. [5] regards the capacity of one cognitive link as an optimization problem with constraints in interference temperature and studies the optimal power allocation strategies. [6] studies the problem of channel selection in multi-hop cognitive mesh networks, but power allocation is not considered. With the assumption that the primary users will always occupy the spectrum, these approaches can sufficiently increase the spectrum efficiency. [7] studies the joint of power control and random access under interference temperature, the optimization problem is transformed to a convex optimization problem. However, each cognitive user should be aware of the interference with the primary users and requires some kind of communications between the cognitive users and the primary users.
Previous works (such as [7]) on conventional OFDM systems are based on an implicit assumption that all the OFDM sub-carriers are fixed and always available. But in practice, the under-utilized spectrum which can be utilized by the secondary users varies over time, this is because the primary users can access to their spectrum unrestricted.
In this paper, we consider an overlay cognitive system, where multiple cognitive users coexist with multiple primary users and the availability of spectrum might not be contiguous because it is used by primary users. The multi-carrier system which dynamically operates in non-contiguous frequency bands and enabled by cognition technology is referred to as NC-OFDM [8]. The flexibility offered by NC-OFDM based CR can be employed to devise spectrum sharing schemes and provides QoS requirements by jointly considering variations in spectrum availability. We integrate the transmit power constraint and fairness of spectrum allocation in this paper. The optimization objective is to maximize the system throughput subject to maximize peak power constraints and minimum QoS requirement on individual cognitive user. The QoS constraint is characterized by the minimum transmission rate requirement. To balance the power and QoS constraints, and further to efficiently and fairly utilize spectrum, transmit power and spectrum allocation must be determined by coordination among cognitive users.
The rest of this paper is organized as follows. The problem formulation and transformation are presented in Section 2. In Section 3, we propose the power and spectrum allocation algorithm based on particle swarm optimization. Section 4 includes simulation results and analysis. Conclusions are drawn in Section 5.
2. Mathmatics Model
In this paper, we consider a cognitive base station to multi cognitive users in wireless networks with rapid changes of spectrum opportunities. When the spectrum opportunities vary quickly, the cognitive users should frequently update the spectrum availably to avoid interference with the primary user. The cognitive base station balances the cognitive users’ transmit power and spectrum to efficiently and fairly utilize spectrum.
Consider OFDM based CR system with a total bandwidth of  Hz and M primary users, each primary user with a bandwidth
Hz and M primary users, each primary user with a bandwidth  (
( ), assume that
), assume that  is less than the coherent bandwidth of the wireless channel, so that the channel response on each is flat. At the same time, there are N cognitive users in this system. At different location and time t, cognitive users have different available spectrum resource information because of the primary users’ transmission activities. Define this available spectrum resource information as
is less than the coherent bandwidth of the wireless channel, so that the channel response on each is flat. At the same time, there are N cognitive users in this system. At different location and time t, cognitive users have different available spectrum resource information because of the primary users’ transmission activities. Define this available spectrum resource information as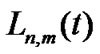 , where
, where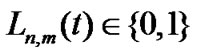 .
. means the mth primary user use its own channel and the nth cognitive user can not use this channel, otherwise
means the mth primary user use its own channel and the nth cognitive user can not use this channel, otherwise . Let
. Let  denote the channel gain of the nth cognitive user on the mth channel and
denote the channel gain of the nth cognitive user on the mth channel and  be the transmit power of the nth cognitive user on the mth channel at time t,
be the transmit power of the nth cognitive user on the mth channel at time t,  is the maximum peak transmit power constraint of user n. We assume that the time variation of the wireless channel is stationary and slow enough, so that the cognitive users are able to perfectly estimate their local channels state information (CSI) on each channel and the cognitive base station knows all the CSI. Based on this CSI, cognitive base station balances the power and spectrum allocation to maximize the system throughput. Let
is the maximum peak transmit power constraint of user n. We assume that the time variation of the wireless channel is stationary and slow enough, so that the cognitive users are able to perfectly estimate their local channels state information (CSI) on each channel and the cognitive base station knows all the CSI. Based on this CSI, cognitive base station balances the power and spectrum allocation to maximize the system throughput. Let  indicate whether the spectrum is allocated to the cognitive user at time t. If
indicate whether the spectrum is allocated to the cognitive user at time t. If , the mth channel is assigned to the nth cognitive user, otherwise
, the mth channel is assigned to the nth cognitive user, otherwise . Each channel can be used by one cognitive user at any given time t, that is interpreted as
. Each channel can be used by one cognitive user at any given time t, that is interpreted as .
.
We assume that the network is under additive white Gaussian noise. We use M-ary quadrature amplitude modulation (MQAM) and then the maximum transmit rate of cognitive user n in channel m is given by:
 (1)
(1)
where  is an SNR gap parameter which indicates how far the system is operating from capacity,
is an SNR gap parameter which indicates how far the system is operating from capacity,  is the interference power.
is the interference power.
The objective is to maximize the cognitive system throughput
 (2)
(2)
since power per user is finite in this system, every cognitive user has its own peak power constraint
 (3)
(3)
In practice, cognitive user transmission rate requirement is required no less than a certain threshold . It is defined as the QoS constraint of each cognitive user and expressed as
. It is defined as the QoS constraint of each cognitive user and expressed as
 (4)
(4)
Note that if the available spectrum information  or the mth channel has not been allocated to the nth cognitive user
or the mth channel has not been allocated to the nth cognitive user , the transmit power must be zero. The base station should optimize the spectrum allocation matrix X and power matrix P. In this problem,
, the transmit power must be zero. The base station should optimize the spectrum allocation matrix X and power matrix P. In this problem, 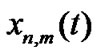 is an element of X and
is an element of X and ,
,  is an element of P and
is an element of P and .
.
Due to the discrete nature of channel and continuous nature of power, this optimization problem is a mixed integer nonlinear programming problem (MINLP). The difficulties in solving this MINLP problem come from the conflicting constraint sets, and coupled control variables. In [7] and many other works, they relax the binary valued constraint on the integer variable and replace it by a continuous variable. While this method causes inaccuracy of the algorithms and it can not find the optimal solution. In this paper, we first transform the MINLP problem to a continuous nonlinear programming (NLP) problem by introducing variable transformation, then we solve this problem by particle swarm optimization algorithm.
We substitute the variable  and
and  by
by
 (5)
(5)
so the variable  is transformed to
is transformed to
 (6)
(6)
Then the optimization problem is transformed as the following problem P1:
P1.
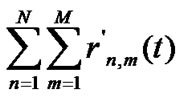
 (7)
(7)
s.t.
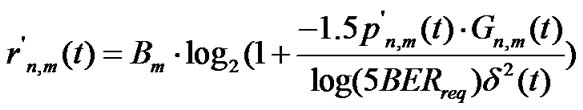 (
( )
)
(8)
 (
(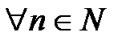 ) (9)
) (9)
 (
(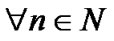 ) (10)
) (10)
 ,
, 
( ) (11)
) (11)
In P1, one continuous variable  replaces the integer variable and the continuous variable, this substitution reduces the solution space dramatically. In addition, the new model is suitable for heuristic and search algorithms.
replaces the integer variable and the continuous variable, this substitution reduces the solution space dramatically. In addition, the new model is suitable for heuristic and search algorithms.
3. Power and Spectrum Allocation Algorithm Based on PSO
The particle swarm algorithm (PSO) is a swarm intelligence optimization algorithm modeled on the flight characteristics of birds [9,10]. In PSO, each solution is a ‘bird’ in the flock and is referred to as a ‘particle’, each particle has a position vector and velocity vector. The location of particles is the solution of optimization problem, the performance of each particle depends on the value of optimization objective’s fitness function. Velocity vector used to determine particle velocity.
The following notation is needed in PSO. The number of particles in the population is denoted as . Let
. Let  be the position of particle i (
be the position of particle i ( ) at iteration k, where D is the number of dimensions to represent a particle and
) at iteration k, where D is the number of dimensions to represent a particle and  is the dth (
is the dth ( ) dimension of the position of particle i. Note that
) dimension of the position of particle i. Note that 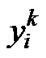 is treated as a potential solution of the optimization problem. The velocity of particle i at iteration k is denoted as
is treated as a potential solution of the optimization problem. The velocity of particle i at iteration k is denoted as ,
,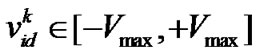 . Each particle in the swarm is assigned a fitness value indicating the merit of this particle such that the swarm evolution is navigated by best solutions. Let
. Each particle in the swarm is assigned a fitness value indicating the merit of this particle such that the swarm evolution is navigated by best solutions. Let 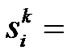
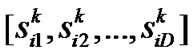 be the best solution that particle i has obtained until iteration k, and
be the best solution that particle i has obtained until iteration k, and  be the global best solution obtained from the population at iteration k.
be the global best solution obtained from the population at iteration k.
The evoluationary process of the PSO is as follows:
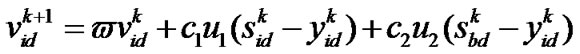 (12)
(12)
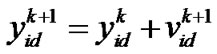 (13)
(13)
where  and
and  are two positive constants named learning factors or acceleration coefficients,
are two positive constants named learning factors or acceleration coefficients,  and
and  are uniform random numbers distributed in the range [0, 1], and
are uniform random numbers distributed in the range [0, 1], and  is an inertia weight employed to control the impact of the previous history of velocities on the current velocity. Note that Equation 12) specifies that the velocity of a particle at iteration k is determined by the previous velocity of the particle, the cognition part, and the social part.
is an inertia weight employed to control the impact of the previous history of velocities on the current velocity. Note that Equation 12) specifies that the velocity of a particle at iteration k is determined by the previous velocity of the particle, the cognition part, and the social part.
In the PSO-based spectrum and power allocation algorithm, each particle's position vector specifies a possible spectrum and power allocation scheme. The penalty function is used to solve the constrained optimization problem. Ordinary penalty function only calculates the total violation of individuals, but does not make full use of the violation information of the infeasible solutions. We use the penalty function which is not only depends on the number of constraint violations but also on the degree of constraint violations. The performance of this method is better than that using the ordinary penalty function [11]. As a result of the different scales in constraints, it is possible that some certain constraints play a dominant role in the total constraints and other constraints may not reflect their degree of constraint violations. In addition, the objective function and the violations of constraint functions may be in different scales, so we normalize the objective function and constraint functions to solve this problem.
We use the following fitness function to evaluate the particle:

 (14)
(14)
where  represents the total amount of the constraint violations and
represents the total amount of the constraint violations and 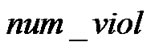 represents the number of the constraint violations. If any user n in particle
represents the number of the constraint violations. If any user n in particle  violates the transmission rate constraint (9) or power constraint (10), the
violates the transmission rate constraint (9) or power constraint (10), the  of
of 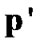 will plus
will plus
one.
 (15)
(15)
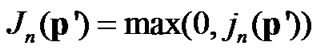 (16)
(16)
 (17)
(17)
 (18)
(18)
 (19)
(19)
where  is the system throughput of the particle
is the system throughput of the particle  in time slot t.
in time slot t.  is an N by M matrix representing the power and channel allocation, if
is an N by M matrix representing the power and channel allocation, if , the channel m is assigned to the cognitive user n, otherwise
, the channel m is assigned to the cognitive user n, otherwise .
.
In the proposed PSO-based power and spectrum allocation algorithm, a particle specifies a possible power and spectrum allocation assignment. As  when
when , if we use one bit to encode every element in
, if we use one bit to encode every element in , there will be a lot of redundancy in the particle. We encode only those elements which may take the value 1, i.e.,
, there will be a lot of redundancy in the particle. We encode only those elements which may take the value 1, i.e., 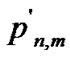 where
where 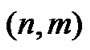 satisfies
satisfies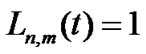 . As a consequence, the length of the coding string is equal to the number of elements equal to 1 in L. Figure 1 illustrates the structure of an example particle, where
. As a consequence, the length of the coding string is equal to the number of elements equal to 1 in L. Figure 1 illustrates the structure of an example particle, where ,
,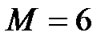 . Note that encoding all the elements needs 30 bits, while encoding only the elements with underline only needs 9 bits. In order to evaluate the fitness of the particle, we need to map the particle to the assignment matrix
. Note that encoding all the elements needs 30 bits, while encoding only the elements with underline only needs 9 bits. In order to evaluate the fitness of the particle, we need to map the particle to the assignment matrix , as the arrows show in Figure 1.
, as the arrows show in Figure 1.
The value of every bit in the particle is randomly generated at the initial population and this coding scheme reduces the searching space of the optimization problem efficiently.
The proposed PSO-based power and spectrum assignment algorithm proceeds as follows:
Step 1: cognitive user gets the available spectrum resource information matrix  and channel information matrix
and channel information matrix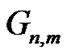 , then transmits these information to the cognitive base station.
, then transmits these information to the cognitive base station.
Step 2: set , and randomly generate
, and randomly generate  and
and , where
, where ,
, , thus obtaining
, thus obtaining ,
,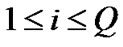 .
.
Step 3: map  (
( ) to
) to , where
, where  is the dth element with
is the dth element with .
.
Step 4: compute the fitness value of each particle in the population according to Equation 14), set  and
and , where b is the index of the particle which has the highest fitness value.
, where b is the index of the particle which has the highest fitness value.
Step 5: set , and update
, and update  according to Equation 12). If
according to Equation 12). If , then set
, then set ; if
; if , set
, set .
.
Step 6: update  according to Equation 13) and map
according to Equation 13) and map  to
to .
.
Step 7: compute the fitness value of each particle in the population. For particle i, if it’s fitness value is greater than the fitness value of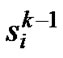 , then set
, then set . If particle i’s fitness value is greater than the fitness value of
. If particle i’s fitness value is greater than the fitness value of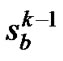 , then set
, then set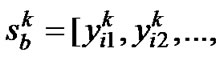 .
. .
.
Step 8: if k equals to the predefined maximum iteration, then the algorithm is terminated, map 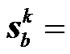
 to
to ; else, go to Step 5.
; else, go to Step 5.
4. Simulation Result and Analysis
To evaluate the proposed algorithm, simulations were performed for the OFDM based CR system. The bandwidth of the OFDM system is  MHz, which is li-
MHz, which is li-
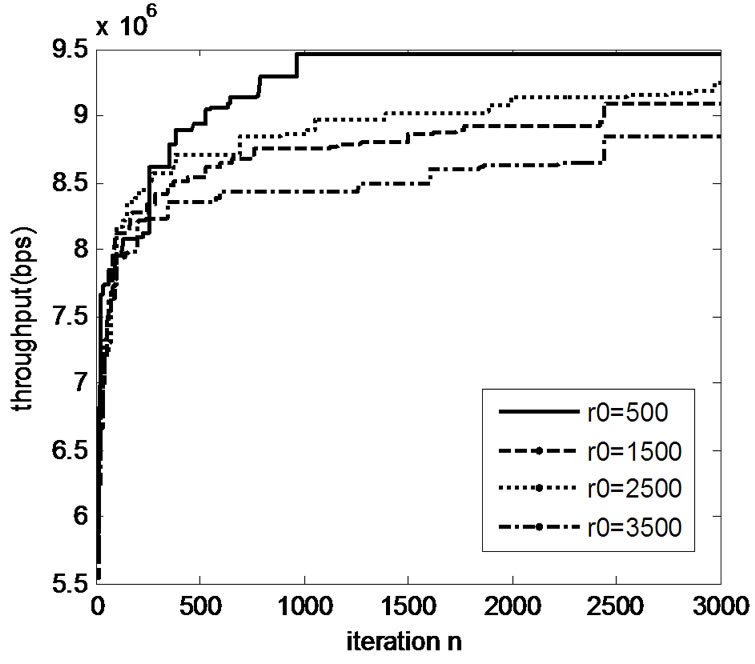
Figure 2. convergence of proposed algorithm under different QoS constraints( )
)
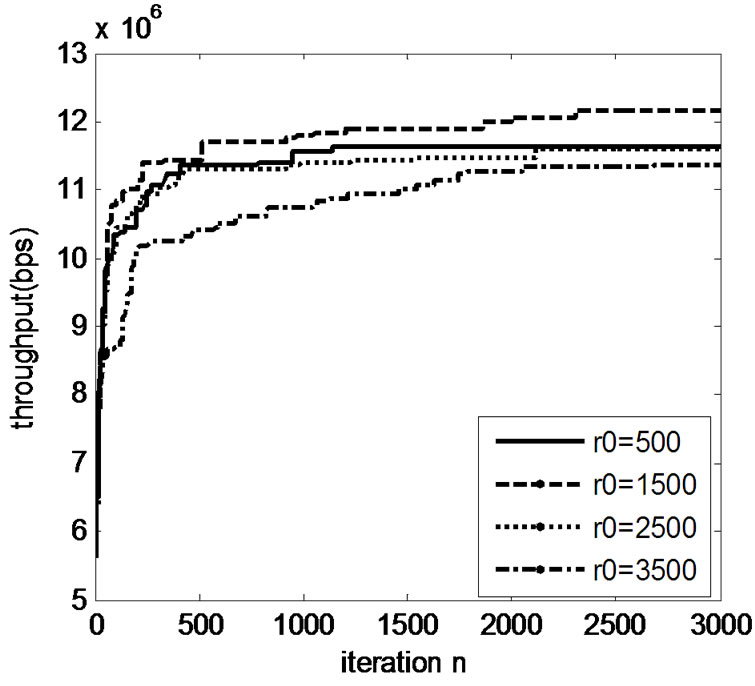
Figure 3. convergence of proposed algorithm under different QoS constraints( )
)
censed to  primary users, every primary user’s transmission uses one channel and the available spectrum resource information matrix L is generated randomly. The number of cognitive users is
primary users, every primary user’s transmission uses one channel and the available spectrum resource information matrix L is generated randomly. The number of cognitive users is . The required bit error rate of each transmission is supposed to be
. The required bit error rate of each transmission is supposed to be . For simplicity, each cognitive link’s average channel gain is chosen randomly within
. For simplicity, each cognitive link’s average channel gain is chosen randomly within  and the interference power is 0.5 mW.
and the interference power is 0.5 mW.
The parameters for the PSO are ,
,  , and
, and , and PSO would be terminated after 3000 iterations.
, and PSO would be terminated after 3000 iterations.
Figure 2 and Figure 3 illustrate the convergence proc-