
1. Introduction
Generally, multi-dimensional signals are represented by vectors, whereas vectors have directivity. For image information, this directivity has become one of the basic characteristics to distinguish multi-dimensional signals from one-dimensional signals. In this paper, the directivity of multi-dimensional signals is defined as “orientation”. The main purpose of orientation estimation is to calculate the orientation information of each point of a multi-dimensional signal, which plays an important role in image processing and machine vision. Orientation estimation has direct applications in edge extraction, image segmentation, texture analysis, adaptive filtering, stereo parallax estimation, image enhancement and motion analysis. The calculation of displacement and optical flow field is also the orientation estimation of signal in three-dimensional space.
According to the representation of orientation, the existing orientation estimation methods can be divided into tensor-based methods and channel-based methods. Tensor-based orientation estimation methods can be divided into two categories: time-domain methods and frequency-domain methods. The time-domain methods mainly include calculation methods based on gradient [1] [2], regularized convolution [3] and signal autocorrelation function [4]. In the frequency domain, orientation estimation is generally the synthesis of filtering results of a group of filters (orthogonal filter or Gabor filter), which can be further divided into the phase-based method and the energy-based method [5]. Among them, the main problem of the gradient-based method is the robustness of gray gradient calculation. For the comparative analysis of the calculation accuracy of different local difference operators in the case of no noise and Gaussian additive noise, see literature [6]; the method based on regularized convolution mainly aims at the case that the signal model can be approximated by polynomials; the method based on the signal autocorrelation function needs a lot of calculation, because the calculation of the signal autocorrelation function itself is much larger than the calculation of the signal gray gradient. This method also needs to determine the principal curvature direction of the autocorrelation function. The channel-representation-based method [7] belongs to the time-domain method, which estimates the orientation by combining the gray gradient with the channel representation. However, these algorithms cannot ensure accuracy and robustness to noises at the same time.
This paper puts forward a principal component analysis method and combines it with the frequency-domain filtering-Lognormal algorithm, which can be called a Lognomal_PCA method. What is more, the differences between principal component analysis and estimation error & robustness to noise are compared through experimental analysis.
2. The Algorithm
The main idea of PCA method is: firstly, impose the Fourier transform to the signal, then to calculate the orthogonal tensor according to the filtering results, and finally obtain the orientation estimation result by principal component analysis.
The frequency domain filter is designed as a separable filter in polar coordinates, i.e.:
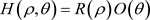 (1)
(1)
where  is the radial distance from a point on the frequency domain plane to the central frequency,
is the radial distance from a point on the frequency domain plane to the central frequency,  denotes the radial function,
denotes the radial function, 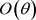 is the orientation angle function. The specific calculation formula is as follows:
is the orientation angle function. The specific calculation formula is as follows:
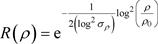 (2)
(2)
Here,  represents the center frequency,
represents the center frequency, 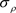 is the scale parameter, log(x) = logₑ(x).
is the scale parameter, log(x) = logₑ(x).
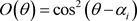 ,
,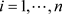 (3)
(3)
where 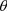 is the radial angle from a point on the frequency domain plane to the center frequency,
is the radial angle from a point on the frequency domain plane to the center frequency, 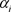 denotes the angle of the filter guide vector, for the two dimensional case, n is set as 3 - 4, Because the proper selection of 3 - 4 direction vectors can form a set of bases of the orientation space.
denotes the angle of the filter guide vector, for the two dimensional case, n is set as 3 - 4, Because the proper selection of 3 - 4 direction vectors can form a set of bases of the orientation space.
After a certain number of orthogonal filters are selected, the image is filtered, and the tensor is constructed according to the obtained output:
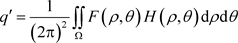 (4)
(4)
Here 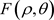 is the Fourier transformation of the input signal.
is the Fourier transformation of the input signal.
The tensor representing orientation information is calculated as follows:
 (5)
(5)
where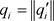 , who are the absolute values of the outputs of several orthogonal filters,
, who are the absolute values of the outputs of several orthogonal filters, 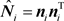 (
(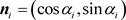 ) represent the tensors constructed for orthogonal filter guidance vector,
) represent the tensors constructed for orthogonal filter guidance vector, 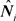 should form a group of basis or a frame of symmetric matrix space,
should form a group of basis or a frame of symmetric matrix space, ![]() is the dual of
is the dual of![]() .
.
After calculating the orientation tensor, the principal component analysis is carried out on the tensor. The later experimental results show that the principal component analysis method can improve the accuracy and robustness of the estimation method to a certain extent than directly estimating the orientation according to the calculated tensor. Principal component analysis [8] is mainly used to calculate the principal vector of a given data set and provide a set of optimized basis for reconstructing the given data in the sense of minimum mean square. The basis of principal component analysis is singular value decomposition of data matrix.
The calculation process of principal component analysis of orientation tensor is as follows:
Firstly, the signal is decomposed by singular value decomposition:
![]() (6)
(6)
where U, V are the left and right singular value vectors of T, which are all orthogonal matrices, S is diagonal matrix, whose diagonal element ![]() is the singular value of T.
is the singular value of T.
Finally, according to the singular value decomposition results, the orthogonal vector corresponding to the larger singular value is selected for orientation estimation, that is, the orientation angle is:
![]() (7)
(7)
Here at an represents the arctangent function, index = {1, 2}, these subscript of singular value vector correspond to larger singular value.
In order to analyze the performance of the algorithm, the angle estimation error of orientation estimation is defined ![]() as:
as:
![]() (8)
(8)
where ![]() is the exact value of orientation tensor,
is the exact value of orientation tensor, ![]() expresses the tensor corresponding to the estimated value, In this method, the tensor representation of the orthogonal vector corresponding to the larger singular value of T.
expresses the tensor corresponding to the estimated value, In this method, the tensor representation of the orthogonal vector corresponding to the larger singular value of T.
If the size of the input image is![]() , The computational complexity of this method is
, The computational complexity of this method is![]() . Here, the computation complexity of Fourier transform is
. Here, the computation complexity of Fourier transform is![]() ; the computational complexity of calculating the filter function matrix is
; the computational complexity of calculating the filter function matrix is![]() ; computational complexity of singular value decomposition of orientation tensor for a single image pixel [8] will be
; computational complexity of singular value decomposition of orientation tensor for a single image pixel [8] will be![]() , Therefore, for the whole image, the computational complexity is
, Therefore, for the whole image, the computational complexity is![]() ,so the computational complexity of the whole algorithm is
,so the computational complexity of the whole algorithm is![]() .
.
3. Experimental Results and Analysis
Three groups of experiments are done in this paper. The first group is imposed on synthetic images, obtaining the estimation error curve of this method and comparing it with other methods; the second group of experiments compared the error between direct estimation and principal component analysis; the third group is to estimate the orientation of the texture of fingerprint image by using the proposed method.
Firstly, through the orientation estimation of the synthetic image with known orientation information, the error curve of the orientation estimation of straight lines with different angles can be obtained, as shown in Figure 1. Here, ![]() ,
,
![]()
Figure 1. Estimation error curve of this method.
![]() . The reason for selecting lines from different angles for estimation is that the discretization error of lines from different angles is different, and there is no discretization error only in some specific directions (such as horizontal and vertical directions).
. The reason for selecting lines from different angles for estimation is that the discretization error of lines from different angles is different, and there is no discretization error only in some specific directions (such as horizontal and vertical directions).
The second group of experiments still use synthetic images to compare and analyze the error size and robustness to noise between principal component analysis and direct estimation. The parameter setting and the corresponding error are demonstrated in Table 1. Figure 2 shows the error comparison without interference (i.e. no cross lines and no noise in the image). The parameters are set according to the suggestions given by the corresponding authors. It can be seen that the addition of principal component analysis reduces the error to less than 0.13; Figure 3 demonstrates the error change curves of both without interference and with many interference lines in the image (the experiment shows that the error will increase when there are cross lines in the image). It can be seen that the principal component analysis method not only has a small error change range, but also the changed error value is smaller than the error value estimated directly without interference; Figure 4 shows the error variation curve of both when Gaussian noise is added. When the variance of the added Gaussian noise changes from 0 to 1, the principal component analysis method is more robust.
![]()
Table 1. Error comparison of different methods.
![]()
Figure 2. Error comparison between principal component analysis and direct estimation (the solid line is the error curve using principal component analysis, and the dotted line is the error curve directly estimated).
![]() (a)
(a)![]() (b)
(b)
Figure 3. Comparison of estimation error with or without interference. (a) Change curve with principal component analysis; (b) Change curve of direct estimation (the solid line indicates no interference and the dotted line indicates interference).
Finally, this paper also makes experiments on fingerprint images. The experimental results are shown in Figure 5. This estimation result reflects the orientation and change trend of fingerprint texture.
![]() (a)
(a)![]() (b)
(b)
Figure 4. Variation curve of estimation error under Gaussian noise. (a) Without discretization error; (b) With discretization error (the solid line is the error variation curve of direct estimation, and the dotted line is the error variation curve of principal component analysis).
![]() (a)
(a) ![]() (b)
(b)
Figure 5. Experimental result of fingerprint image. (a) Original image; (b) Vector diagram of orientation estimation results.
4. Conclusions
For a long time, orientation estimation is a neglected research content in the field of image processing in China. This paper first defines its difference with direction, then makes a comprehensive summary of the research work in this field, and puts forward a lognormal_PCA method which is used for orientation estimation, and its computational complexity is![]() . Finally, the method is verified and analyzed by experiments. The comparison and analysis of the estimation errors of the principal component analysis method and direct estimation method show the advantages of adding principal component analysis.
. Finally, the method is verified and analyzed by experiments. The comparison and analysis of the estimation errors of the principal component analysis method and direct estimation method show the advantages of adding principal component analysis.
Orientation estimation is one of the important contents of image bottom processing. There are still some problems to be solved in the current research [8], such as the balance between calculation cost and estimation accuracy in estimation methods, some problems caused by image digitization, multi-scale analysis and so on. These are the works of further research.