Empiricism, Rationalism, and the Kantian Synthesis from the Quantum Linguistic Point of View ()
1. Introduction
1.1. Quantum Language
It is sure that the main theme of philosophy is “How Do We Live?” to answer this question, philosophers preferred to discuss it in “the world including us” (=dualistic worldview). On the other hand, it is well known that quantum mechanics is also constructed under a dualistic worldview. If so, I would like to pursue “Is the dualism of philosophy related to the dualism of physics?” This is my motivation for writing this paper.
Hence, throughout this paper, I devote myself to the scientific aspect of philosophy.
Recently, in refs. (Ishikawa, 1997a, 1997b, 2006, 2011), we proposed quantum language (or, QL, measurement theory, MT), which is characterized as the linguistic turn of quantum mechanics (as seen in (†) in Figure 4 later). QL has a great linguistic power to describe both classical and quantum systems. Thus, we think that quantum language can be viewed as the language of science, or the perfection of the philosophy of science (Ishikawa, 2019a).
The location of QL (=quantum language) in the history of the world-descriptions is shown in Figure 1 (Ishikawa, 2012a; 2019b; 2021b).
Therefore, QL has several aspects, e.g., physical aspect (Ishikawa, 1991a, 1991b, 2011, 2015, 2017b), system theoretical aspect (Ishikawa, 1997a, 1997b, 1998, 2000, 2008, 2012b, 2012c, 2012d), and philosophical aspect (Ishikawa, 1998, 2017a, 2018, 2019a, 2020, 2021a; Ishikawa & Kikuchi, 2021).
![]()
Figure 1. The history of the world-descriptions.
Thus, we assert that QL is the scientific completion (i.e., the destination) of dualistic idealism.
If so, we can use QL to rate many dualistic theories, that is, we can introduce the concept “progress” in the dualistic theories such as [“X” ⟹ QL“Y”] means that “Y” is more like “QL” than “X”. Thus, [“X” ⟹ QL“Y”] can be interpreted as [“Y” is more scientific than “X”].
And we can assert (Ishikawa, 2021b, 2022) that

and

Philosophy has various aspects, but I think that the scientific aspect of philosophy is to create a “language of science”. Thus, (A1) above is reasonable since quantum language is being proposed as the “language of science”. This (A2) will be reconsidered in Remark 6 later.
Readers may ask the following question:
(B) Why was progress in philosophy (A1) so slow?
This will be answered at the end (i.e., (V2) in 4. Conclusions).
1.2. The Purpose of This Paper
As shown in the following section, quantum language has the following form:

In this paper, we discuss Cartesian and Kantian epistemology, i.e., ⑨ in Figure 1.
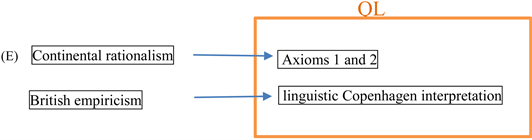
“British Empiricism vs. Continental Rationalism”: Descartes, Spinoza, Leibniz, John Locke, Berkley, Hume, Kant) in relation to QL. “Axioms 1 and 2 (measurements and causality)” and “linguistic Copenhagen interpretation” are in the positions that Figure 2 shows (I have an opinion that both Spinoza’s theory and Leibniz’s theory are not connected to science).
Our purpose of this paper is to explain Figure 2 (or equivalently, (E) later).
It may be the established theory to think of this “vs.” as “tabula rasa vs. nativism”. And Kant is said to have settled this dispute in an integrated manner. However, I think that the “tabula rasa vs. nativism” argument was, after all, nothing more than a kind of word game. This has never been discussed from the standpoint of science. I do not think that the “tabula rasa vs. nativism” problem will lead to productive philosophical discussions.
![]()
Figure 2. The positions of axioms 1 and 2, and the linguistic Copenhagen intepretation.
Therefore, in this paper, we assert that:
(D) From a scientific point of view, “continental rationalism and British empiricism” are not “tabula rasa vs. nativism”, but are related to “Axioms 1 and 2” and “linguistic Copenhagen interpretation” of QL(C), respectively. Continental rationalism (Spinoza, Leibniz) challenged the proposal of an axiomatic formulation of mind-body dualism (improvement of Descartes), although this was clearly the unsolvable problem at the level of physics and mathematics of the time. We believe that these are realized as axioms 1 and 2 of QL. On the other hand, British empiricism (i.e., Locke, Berkeley, Hume, Kant) is brain-scientific (without experiments), and Kant’s theory is the culmination of all these. Their claims have many similarities with the linguistic Copenhagen interpretation in (C). Therefore, we consider the “vs.” of “British empiricism vs. continental rationalism” to be “axiomatic vs. empirical”. If so, we can conclude that British empiricism and continental rationalism respectively correspond to the linguistic Copenhagen interpretation of QL and the axioms of QL, and the two are integrated by QL.
That is, we will conclude the following “scientific progress”:
This will be discussed in the following sections.
2. Axiomatic Theory (QL (i.e., Axioms and 2) and Continental Rationalism)
2.1. Axiomatic Theory in QL (i.e., Axioms 1 and 2)
In this section, we will study Axioms 1 and 2 (i.e., measurement axiom and causality axiom), which is characterized the axiomatic part of QL as shown in (C).
That is:
(F1) Axiom 1 asserts the relation among “mind (=observer)”, “body (=observable) and “matter (=system)”.
(F2) Axiom 2 is like Newtonian kinetic equation (or, Schrödinger equation).
Therefore, it suffices to consider “axioms” = “laws”.
2.1.1. Axiom 1 (Measurement)
Now let us explain QL as follows. For simplicity’s sake, we will discuss a simple case instead of a general setting. See (Ishikawa, 2019b) for a general explanation.
Quantum language (=QL, measurement theory, or, MT) in (C) is, by an analogy of quantum mechanics, constructed as the mathematical theory formulated in a certain C*-algebra A (i.e., a norm closed subalgebra in B(H) (Sakai, 1971; von Neumann, 1932)) as follows:
The pair [A, B(H)] is called a basic structure. When
, the C*-algebra composed of all compact operators on a Hilbert space H, the (C) is called quantum measurement theory (or, quantum system theory), which can be regarded as the linguistic aspect of quantum mechanics. Also, when A is commutative (that is, when A is characterized by C(Ω), the C*-algebra composed of all continuous complex-valued functions vanishing at infinity on a locally compact Hausdorff space Ω (Yosida, 1980). The (C) is called classical measurement theory. Thus, we have the following classification:
That is, this theory covers several conventional system theories (i.e., statistics, dynamical system theory, quantum system theory, etc.).
Now we shall explain the measurement theory (C). Let
be a C*-algebra and let
be the dual Banach space of A. That is,
, and the norm
is defined
by
. Define the mixed state
such that
and
for all
such that
. And put
(1)
A mixed state
is called a pure state if it satisfies that “
for some
and
” implies
. Put
, which is called a state space. It is well known that
, and
, where
. The latter implies that
can be also identified with Ω (called a spectrum space or maximal ideal space) such as:
(H) (state space)
.
Here, assume that the C*-algebra
has the identity I. This assumption is not unnatural, since, if
, it suffices to reconstruct the above A such that it includes
.
Definition 1 According to the noted idea (Davies, 1976) in quantum mechanics, an observable
in A is defined as follows:
1): [Field] X is a finite set,
is the power set of X.
2): [Finite additivity] F is a mapping from F to A satisfying: (a): for every
,
is a non-negative element in A such that
, (b):
and
, where 0 and I is the 0-element and the identity in A respectively. (c): for any
such that
, it holds that
.
With any system S, a basic structure [A, B(H)] can be associated in which QL of that system can be formulated. A state of the system S is represented by an element
and an observable is represented by an observable
in A. Also, the measurement of the observable
for the system S with the state ρ is denoted by
or more precisely,
. An observer can obtain a measured value
by the measurement
.
Axiom 1 presented below is a kind of mathematical generalization of Born’s probabilistic interpretation of quantum mechanics. And thus, it is a statement without reality.
Axiom 1 [Measurement] The probability that a measured value
obtained by the measurement
belongs to a set
is given by
.
2.1.2. Axiom 2 (Causality)
Next, we explain Axiom 2 in (C). Let
be a finite tree, i.e., a partial ordered finite set such that “
and
” implies “
or
”. Assume that there exists an element
, called the root of T, such that
(
) holds. Put
. For example, see Figure 3, where
is the parent map.
The family
is called a Markov relation (due to the
Heisenberg picture), if it satisfies the following conditions 1) and 2).
1): With each
, a C*-algebra
(or a basic structure
is associated.
2): For every
, a Markov operator
is defined. And it satisfies that
holds for any
.
![]()
Figure 3. Tree: (T = {t0, t1, ···, t7}, Π: T\{t0} → T).
The family of dual operators
is called a
dual Markov relation (due to the Schrödinger picture). However, it is not formally used in measurement theory.
Now Axiom 2 in the measurement theory (C) is presented as follows:
Axiom 2 [Causality] The causality is represented by a Markov relation
.
For the further argument (i.e., the W*-algebraic formulation) of measurement theory, see ref. (Ishikawa, 2019b).
Remark 2. Note that Axioms 1 and 2 are, respectively, characterized as the mathematical generalizations of Born’s quantum measurement theory (i.e., the probabilistic interpretation of quantum mechanics) and Heisenberg’s quantum kinetic equation (i.e., Schrödinger equation). Therefore, Axiom 1 and Axiom 2 canno longer be considered statements in physics.
That is, note that:
(I1) the above two axioms are kinds of spells (i.e., incantation, magic words, metaphysical statements), and thus, it is impossible to verify them experimentally. What we should do is not to understand the two, but to learn the spells (i.e., Axioms 1 and 2) by rote. And all we must do is to improve our linguisticability to use these spells.
In this sense, quantum language is a kind of metaphysics (=idealism). Therefore, (I2) the formation of quantum languages depends on human marvelous language ability.
2.2. Axiomatic Theory (in Continental Rationalism)
An axiomatic approach to dualism was first proposed by Descartes (Descartes, 2004). He started from the famous cogito proposition “I think therefore I am”, and he asserted that the existences of “mind”, “body” and “God” were deduced from the cogito proposition, and proposed mind-body dualism (=mind-matter dualism). Descartes considered that,
(J) “mind” and “body (=matter)” are completely separate. Matters (or, bodies) are governed by physical law, but the mind is governed by something other than physical law. Thus, there is no interaction between “mind” and “body”.
Inspired by the (J), Spinoza and Leibniz (i.e., Continental rationalism) also pursued an axiomatic system for mind-body dualism (“Ethica” (Spinoza, 2018), “Monadology” (Leibniz, 1991)). In hindsight, with the knowledge of mathematics and physics at that time, their challenge was scientifically impossible. Spinoza only set up a convenient “axiomatic system” to preach his ethics. The genius Leibniz has only tried the impossible.
I think that the only successful outcome of Descartes is (J). In fact, it would not be an exaggeration to say that almost all philosophies after Descartes are influenced by “mind-body dualism”. Continental rationalism succeeded in spreading the concept of mind-body dualism (J), but it did not succeed in creating an axiomatic system of mind-body dualism. However, there is no guarantee that our idea (in Axioms 1 and 2 in Section 2.1) is the only solution. The pursuit of an axiomatic theory of dualism should be continued.
3. Empirical Theory (the Linguistic Copenhagen Interpretation and British Empiricism)
3.1. What Is the Linguistic Copenhagen Interpretation?
As mentioned in Remark 2, Axioms 1 and 2 (measurement and causality) are spells (
metaphysical statements). Also, quantum language (i.e., QL) is a language, so you may not be able to use it well at first.
It is necessary to practice and master it through trial and error. It’s the same as a toddler learning a language.
Now, even though it is the same process as a toddler learning a language, it is natural that he wants to learn QL as quickly as possible.
(K) If you want to master QL as quickly as possible, you need an instruction manual to use Axioms 1 and 2.
Hence, we define “the linguistic Copenhagen interpretation” as follows.
(L) The linguistic Copenhagen interpretation = the manual to use spells (i.e., Axioms 1 and 2).
Also, note that the definition of “the Copenhagen interpretation of quantum mechanics” is not clear (cf. (Howard, 2004)).
Remark 3 There were two streams in brain-scientific epistemology (without experimentation): continental rationalism, which recognized innate ideas (Descartes, Spinoza, Leibniz), and British empiricism, which insisted on “tabula rasa” (Locke, Berkeley, Hume). Kant is said to be the synthesis of the two. Kant’s theory was popular among philosophical enthusiasts. However, I think that brain-scientific epistemology (without experimentation) and linguistic epistemology are confused in the debate of continental rationalism and British empiricism. In this paper, we are interested in linguistic epistemology and not brain-scientific epistemology (without experimentation). Mathematics is continental rationalistic, with language deduced solely from the axioms of set theory. Everyday language is a language that can be learned through experience, without axioms, and is therefore British empirical. And quantum language has a structure like (C), which is Kantian. The two above (i.e., brain-scientific epistemology and linguistic epistemology) are quite similar. For example, the “primary quality” and “secondaryquality” of Locke correspond to “state” and “observable” in the language of quantum language.
Therefore, in what follows, we will show that many of the words of the great philosophers have become the linguistic Copenhagen interpretation.
3.2. Copernican Revolution
Before discussing the similarity between the linguistic Copenhagen interpretation and British empiricism (i.e., Kantian epistemology), let me explain the Kant’s Copernican revolution. I consider Kant’s epistemology to be the perfection of British empiricism.
The public may have the impression that Kant was bragging about his ideas as the “Copernican revolution,” but the following diagram will show that the “Copernican revolution” is a powerful method of creating idealism (i.e., transcendental idealism) from realism. Recall 9 , 11 , 13 in Figure 1. More precisely, these are explained in Figure 4.
As seen in (†) in Figure 4, QL is regarded as the Copernican revolution (or, the linguistic turn) of quantum mechanics. Since Axioms 1 and 2 are mathematical generalization of the principles of quantum mechanics, there are many hints in quantum mechanics for using QL. A quick study of quantum mechanics is quite an effective way to master quantum language.
Remark 4. Understanding quantum mechanics is not essential to using quantum language. Even if you don’t know quantum mechanics, you can learn quantum language by solving many simple exercises concerning classical QL (G2) in (Ishikawa, 2019b). In my university lecture, this method made it easy for students without prior knowledge of quantum mechanics to learn quantum language.
![]()
Figure 4. Several Copernican revolutions (from realism to idealism).
3.3. There Is No Interaction between “Mind” and “Body” (Due to Descartes)
The Copenhagen interpretation asserts that (M) Use quantum language (axioms 1 and 2), imagining Figure 5 below!
In Figure 5, we remark:
(N1) a : it suffices to understand that “interfere” is, for example, “apply light”. b : the reaction, c : perceive it.
That is, “measuring instrument looks into a system and pass it on to us.” However, (N2) in measurement theory (=quantum language), “interaction” must not be emphasized, since there is no interaction between “mind” and “body” (or equivalently, “mind (=observer)” and “body (or, matter)” are completely separated), which was, for the first time, asserted by Descartes.
Therefore, to avoid confusion, it might be better to omit the interaction a , b and c in Figure 5.
After all, we think that:
(N3) there is no measured value without observer (i.e., “I”, “mind”). Thus, we consider that measurement theory is composed of three keywords: “observer (measured value)”, “observable”, “state” (Ishikawa, 2021b).

Hence, quantum language is based on dualism, i.e., a kind of mind-matter dualism.
The measurement
does not depend on the choice of observers. That is, any proposition in quantum language is not related to “observer” (=“I”), therefore, there is no “observer’s space and time” in quantum language. And thus, there is no tense (i.e., past, present, future).
![]()
Figure 5. [Descartes figure]: Image of “measurement (= a , b , c )”.
Remark 5. 1): In the above three, “observable (=measuring instrument)” may be the most difficult to understand. For example, if a compass is a directional measuring device, then the North Star can be also regarded as a directional measuring device. This kind of fun becomes the subject of philosophical essay (e,g., “Le visible et l’invisib” (cf. (Merleau-Ponty, 1964))).
2): For example, assume that an apple is put on food scale. We are not sure if he is trying to weigh an apple or make sure the food scale isn’t broken (see Figure 6). Thus, the difference between “body” and “matter” is arbitrary. This is determined by the observer. Both “body” and “matter” obey the laws of physics. However, the laws governing “mind” are assumed to be unknown. Maybe there is no such thing.
3.4. Only One Measurement Is Permitted (Due to Parmenides (BC.520-BC.450)
Parmenides, the ancient Greek philosopher, said:
(O1) Everything does not change. There is no motion and no change. Time does not exist. There exists only “one”, and not “many”.
I don’t know what Parmenides really meant, but this is very similar to the following Copenhagen interpretation:
(O2) Only one measurement is permitted.
If so, the state after a measurement is meaningless because it cannot be measured any longer, and hence, it does not exist (from “To be is to be perceived” (by G. Berkley). Thus, the collapse of the wavefunction is prohibited (cf. (Ishikawa, 2015); projection postulate).
We are not concerned with anything after measurement. Strictly speaking, the phrase “after the measurement” should not be used.
Also, Parmenides’ saying (O1) is similar to the following linguistic Copenhagen interpretation:
(O3) A state never moves.
Thus, the Heisenberg picture should be adopted, that is, the Schrödinger picture should be prohibited. wavefunction collapse does not exist.
Also, we must emphasize the following.
![]()
Figure 6. Which is a measuring device (i.e., body), the apple or the food scale?
(O4) “To be is to be perceived” (by G. Berkley).
This is related to Bohr-Einstein controversy, which is the biggest scientific debate of the 20th century (cf. (Einstein et al., 1935; Bohr, 1935). This is the question, “Is the concept of measurement an essentialization of physics or not?” Einstein argued that this was unnecessary and said, “The moon is there even when we are not looking at it”. This issue has not yet been settled today. However, quantum language argues that the concept of measurement is necessary for science (science in the broad sense, not limited to physics).
Also, note that the (O4) is similar to Popper’s falsificationisn (Ishikawa, 2019a).
3.5. Space-Time
3.5.1. Observer’s Space-Time Does Not Exist
Recall the above (O1): “Time does not exist”. We consider that this means that (P) While “matter” is in the space-time, the observer is not.
This is also one of the linguistic Copenhagen interpretation. That is, observer’s space-time does not exist. Thus, the question: “When, where and by whom was the measured value obtained?” is out of the scope of measurement theory. Thus, words such as “now”, “here”, and “I” should not be used in a scientific proposition. If you are going to use it, you need to be very careful. That is, there is no tense either in measurement theory or in science. The “tense” is a treasure trove of word play (cf. McTaggart’s paradox, Russell’s five-minute hypothesis, ref. (Ishikawa, 2018).
3.5.2. Matter’s Space-Time: Leibniz-Clarke Correspondence (1715-1716)
Let us explain Leibniz-Clarke Correspondence (1715-1716: cf. (Ishikawa, 2018)), which is important to know both Leibniz’s and Clarke’s (≈Newton’s) ideas concerning space and time.
(Q1) [The realistic space-time] Newton’s absolutism says that the space-time should be regarded as a receptacle of a “thing.” Therefore, even if “thing” does not exit, the space-time exists.
On the other hand:
(Q2) [The metaphysical space-time] Leibniz’s relationalism says that:
(i): Space is a kind of state of “thing”.
(ii): Time is also a kind of ordered set, which represents an order of occurring in succession which changes one after another.
I assert that Leibniz’s relationalism (Q2) can be realized in QL as follows:
(R) (i): Let [A.B(H)] be a basic structure. Then, the space Ω is represented by some commutative C∗-algebra C(Ω) such that C(Ω) ⊆ A.
(ii): Time axis T’ is a linear sub-ordered set of T (e.g., see Figure 3).
cf. refs. (Ishikawa, 2018; Ishikawa & Kikuchi, 2021).
3.6. Causality in the Linguistic Copenhagen Interpretation
The following are three theories on causality.
(S1) [Realistic causality (Newton)]: Newton advocated the realistic describing method of Newtonian mechanics as a final settlement of accounts of ideas, such as Galileo, Bacon, and Descartes, and he thought as follows:
“Causality” actually exists in the world. Newtonian equation described faithfully this “causality”. That is, Newtonian equation is the equation of a causal chain.
This realistic causality may be a very natural idea, and you may think that you cannot think in addition to this. In fact, probably, we may say that the current of the realistic causal relationship which continues like Newtonian mechanics → Electricity and magnetism → Theory of relativity → …is the mainstream of science.
However, there are also other ideas, i.e., three “non-realistic causalities” as follows.
(S2) [Cognitive causality]: David Hume, Immanuel Kant, etc. thought as follows. We cannot say that “causality” actually exists in the world, or that it does not exist in the world. And when we think that “something” in the world is “causality”, we should just believe that it has “causality”. That is, the cognition circuit of causality is installed in the brain, and when it is stimulated by “something” and reacts, we think “there is causal relationship.”
In that follows, we show our proposal (i.e., linguistic causality):
(S3) [Linguistic causality]: The causal relationship of measurement theory (=QL) is decided by the Axiom 2 (causality). If I say in detail: Although measurement theory consists of the two Axioms 1 and 2, it is the Axiom 2 that is concerned with causal relationship. When describing something in quantum language (i.e., a language called measurement theory) and using Axiom 2 (causality), we think that thing has causality.
Note that “linguistic turn: (S2)→(S3)” is realized by 10 in Figure 1.
Remark 6 As shown in this paper, quantum language has two aspects (i.e., axiomatic theory (=Axioms1 and 2) and empirical theory (the linguistic Copenhagen interpretation)).
The symbol “X ⟹ QLY”can be used to mean three meanings.
(i): Y is closer to Axioms of QL than X.
(ii): Y is closer to the linguistic Copenhagen interpretation than X.
(iii): Comprehensive judgment considering both (i) and (ii).
Under the sense of (i), we concluded (cf. ref. (Ishikawa, 2022)) (B), namely,

That is, I asserted Thomas’s scientific advantage over Descartes since the most fundamental concept “universal” in a scientific worldview was neglected in Cartesian and Kantian philosophy.
However, if (ii) is assumed, then most people (myself included) might agree to the following.
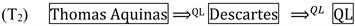
In the case of (iii), opinions will be divided depending on the weight of (i) and (ii). However, if the majority of philosophical enthusiasts decide, (T2) must be chosen.
4. Conclusion
Throughout the history of western philosophy, “British empiricism vs. Continental rationalism” is the most interesting theme. It may be the established theory to think of this “vs.” as “tabula rasa vs. nativism”. And Kant is said to have settled this dispute in an integrated manner. This story may be popular with the average philosophy enthusiast. However, I think this is too simplistic a view. In fact, the argument about “tabula rasa vs. nativism” is not scientific. I am well aware that “being scientific and logical” is not the highest priority in philosophy, but in this paper, I stuck to being scientific.
The purpose of this paper was to reconsider “British empiricism vs. Continental rationalism” from the standing-point of quantum language (=“Axioms (measurement and causality)” + “the linguistic Copenhagen interpretation”). And we conclude the following “scientific progress” (U)(=(E)):
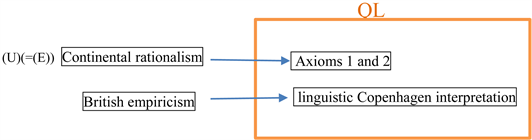
That is, continental rationalism and British empiricism are synthesized in QL.
I think this result is much more interesting than we originally expected. That is, the above (U) encourages us to think as follows.
(V1) these two (i.e., continental rationalism and British empiricism) were actually one theory, just like quantum mechanics is founded on physical laws (Born’s probabilistic interpretation and the Schrödinger equation) and the Copenhagen interpretation.
If so, for the first time, we were able to understand the meaning of “continental rationalism vs. British empiricism” in science.
And further, if so, we can answer question (B) as follows.
(V2) This is because the history of philosophy (A1) is like studying the Copenhagen interpretation without knowing the laws (i.e., Born’s probabilistic interpretation and the Schrödinger equation).
In other words, our result asserts the following two questions are equivalent:
(W1) Why did continental rationalism and British empiricism arise after Descartes?
(W2) Why is quantum mechanics made up of axioms and interpretations?
This (W2) is an unsolved problem in physics in the following sense:
(X1) Newton mechanics and the theory of relativity do not have “interpretation”.
Why is quantum mechanics the only one that has an “interpretation”?
I have the following opinion that:
(X2) Even Newtonian mechanics (or disciplines other than mathematics) must have an “interpretation”. However, since it is almost self-evident, the public is not aware of it.
I do not, however, have a proof for this.
Thus, my concern is not an old problem, but an up-to-date one. I hope that my assertions will be examined from various points of view.