1. Introduction
Nonlinear partial differential equations (NPDEs) are encountered in various fields such as physics, chemistry, biology, mathematics and engineering. Most nonlinear models of real-life problems are still proving difficult to solve either numerically or theoretically. Recently, much attention has been devoted to the search for better and more efficient solution methods for determining a solution, approximate or exact, analytical or numerical, for nonlinear models [1].
Many methods have been developed to solve a dissipative wave equation, including the non-polynomial spline method and the cubic B-spline method. Researchers who have used the non-polynomial spline method include El-Danaf and Faisal (2009), who used a non-polynomial spline-based method to obtain numerical solutions for a dissipative wave equation. The developed method was shown to be conditionally stable for the given values of specified parameters. Furthermore, the obtained numerical results reveal that their proposed method maintains good accuracy [2]. Zaki Ahmed et al. (2020) used a non-polynomial spline function to obtain numerical solutions for a dissipative wave equation at middle points for lattice in space direction and at the same time. The presented method was shown to be conditionally stable. In addition, the computational results revealed that their proposed technique was suitable for the solution of these equations and agreed with the true solutions [3]. The cubic B-spline has been employed by many researchers to solve nonlinear dissipative wave equations. The most recent relevant results are those presented by Alaofi et al. in 2021. The stability analysis investigation demonstrated that the method is conditionally stable. The developed method is shown to be conditionally stable for given values of specified parameters. The obtained numerical results indicate that the proposed method maintains good accuracy [4]. As the previous two methods, non-polynomial spline and cubic B-spline, have been used many times in recent years, we wanted to present a comparison between them to assist future researchers. Section one outlines some previous studies on the nonlinear dissipative wave equation. Section two offers basic definitions and descriptions of the non-polynomial spline functions, local truncation errors, and the cubic B-spline method. The third section will describe the stability analysis. Using the concept of stability and the von Neumann method, three stability-related cases are provided. Section four addresses numerical illustration. In this section, we offer an example from each author as well as their results. We have also presented additional results that we have obtained during our research. In the final section, we offer some conclusions and highlight some areas for further development.
The generalised nonlinear dissipative wave equation of the form [5]:
(1)
under the boundary conditions:
(2)
and initial conditions:
(3)
2. The Methods
In this section, we will illustrate the non-polynomial spline method and the cubic B-spline method.
2.1. Non-Polynomial Spline Method
The Non-polynomial Spline Functions [6]
Let
be a subdivision of the interval
. The non-polynomial spline function is defined by
where
is a mixed spline function of the form:
and r represents the degree of the polynomial part.
Remark
We can use other functions as
,
,
and
instead of
in
.
Local truncation error [6]
The truncation error is the difference between the differential equation and its approximating difference equation. Let
represent the differential equation at the
mesh point. If u is replaced by U at the mesh points of the difference equation, then the value of
is named the local truncation error at the
mesh point. We denote it by
.
Zaki Ahmed [3] et al. and El-Danaf [2] et al. used the non-polynomial spline method.
To set up the non-polynomial spline method, select an integer
and time-step size
. With
, the mesh points
are:
and,
Let
be an approximation to
, obtained by the segment
of the mixed spline function passing through the points
and
. Each segment has the forms (4) and (5) as follows:
Zaki Ahmed et al. used the following form,
(4)
El-Danaf et al. used the following form,
(5)
where
;
;
and
are unknowns to be determined and
is a parameter of the trigonometric functions.
The truncation error for Equation (4) at
is as follows:
to make
of order
.
The approximation with local truncation error of
:
.
2.2. The Cubic B-Spline Method
The cubic B-spline functions
are defined by:
where
. The values of the cubic B-spline
and its first and second derivatives vanish outside the interval
. We establish the values of
and its derivatives at the knots in Table 1.
This type of spline is used to obtain an approximate solution to partial differential equations, see [4].
The Analysis and the Initial State for the Dissipative Wave Equation
1) The approximate solution of the dissipative wave equation is considered to be:
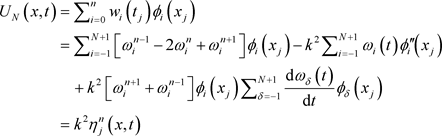
![]()
Table 1. The values of
and its derivatives with knots at the shown points.
where
represents the spline functions, and
represents the unknowns to be determined.
2) The dissipative wave equation reduced to system of ODE.
They get:
3) Using the boundary conditions to get
equations in
unknowns.
,
.
4) Apply the initial conditions to get the independent variables:
5) After getting the following system of algebraic equations:
6) Two initial conditions are applied to get the following system:
7) Adding the following two initial conditions to complete the system of equations:
3. The Stability Analysis
Stability [7]
Suppose that, in a computation involving a difference scheme, an error
is introduced at a time level
, and suppose that no further errors occur. If
denotes the error resulting from this error at time
, then the scheme is stable if
remains bounded as
(i.e., the error must not grow without limit).
Stability by the Fourier series method (Von Neumann’s Method) [7]
This method, developed by Von Neumann during World War II, was first discussed in detail by O’Brien, Hyman and Kaplan in a paper published in 1951. It expresses an initial line of errors in terms of a finite Fourier series, and considers the growth of a function that reduces to this series for
using a “variables separable” method identical to that commonly used for deriving analytical solutions to partial differential equations. If we write
in the difference scheme, and if it is linear, then
will satisfy the same equation as
expresses the error as a finite Fourier series of the form
. Furthermore, if the equation is linear, then we need consider only the growth of a single form:
where
, and let:
,
where g is called the growth of an amplification factor. For stability, the Von Neumann condition requires:
.
i.e. the error will not increase as t increases.
It should be noted that this method applies only to linear difference equations with periodic initial data. The criterion
is necessary and sufficient for three or more level equations—though it is always necessary. In practice, the method often gives useful results even when its application is not fully justified.
According to the Von Neumann technique we have:
(6)
where
,
is the mode number, h is the element size, and
is the amplification factor.
For stability, we must have
. Also, from Equation (6) we can observe that the product of the two values of
is clearly unity. So, three cases arise.
Case 1: Both the roots are equal to unity. In this case, the discriminant of the quadratic Equation (6) is zero.
Case 2: One of the roots is greater than unity. In this case, the discriminant is greater than zero. This means the stability condition, that is
, is not satisfied. In other words,
would grow in an unbounded manner.
Case 3: The discriminant is less than zero, that is:
. Thus, for stability:
(7)
[2] and [3] using Equation (6), the above inequality becomes:
(8)
Two cases will be discussed:
Case 1: For
, inequality (8) becomes:
We can say that our system is stable for
,
, and
such that
, and
are small enough.
Case
For
,
, the quantity
is positive, so we can say that stability in this case requires
,
, and
such that
and
are small enough and
.
On the other hand, [4] using Equation (6), the (7) inequality becomes:
. (9)
After simplifying inequality (9), we get:
,
If h is small enough, the method is conditionally stable.
4. Numerical Illustration
Example. Consider the dissipative wave equation [8]:
(10)
with the initial conditions:
, (11)
and the boundary conditions:
. (12)
4.1. The Results of [2]
Table 2 shows maximum error occurred at 0.5, 1.5, 2.5, and 3.5 respectively. Numerical values have been computed using the non-polynomial spline method and reported in Table 3 & Table 4. The simulation is done up to x = 0.8π. We
![]()
Table 2. The L∞ error for the numerical and exact solutions when
,
,
;
.
![]()
Table 3. Comparison between the numerical and exact solutions at
;
;
;
.
can conclude that applying nonpolynomial splines in the solution of partial differential equations is a promising approach.
4.2. The Results of [3]
L∞ error norms are reported in Table 5. In addition, comparisons of approximate and exact solutions at different nodes x and different time levels are reported in Table 6 & Table 7.
The relation between time and the maximum error is shown in Figure 1 and
![]()
Table 4. Comparison between the numerical and exact solutions at
;
;
;
.
![]()
Table 5. The maximum absolute errors at
,
,
and
.
![]()
Table 6. The true and numerical solution at
,
,
,
and
.
![]()
Table 7. The true and numerical solution at
,
,
,
and
.
![]()
Figure 1. The relation between time and maximum error as per Table 5.
the graph of exact and approximate solutions for different time levels are depicted in Figure 2.
4.3. The Results of [4]
To make a comparison quantitatively, they have computed the error norms L∞ in Table 8. Moreover, the comparison of obtained numerical results with the cubic B-spline method is presented in Table 9 & Table 10 when t = 0.2 and t = 2.
Figure 3 & Figure 4 depict a comparison of exact and approximate solutions when t = 2 and t = 5.
In the following section, we introduce the numerical results, which have been obtained by [4].
![]()
Figure 2. The true solution (green) and numerical solution (red) at
,
,
,
and
.
![]()
Table 8. The L∞ error for the numerical and exact solutions when k = 0.01,
from t = 0.5 to t = 2.0.
![]()
Table 9. Comparison between the numerical and exact solutions at t = 0.2, k = 0.002,
.
4.4. Our Results
In Table 11, the computational maximum errors with respect to the exact solution and numerical solution.
![]()
Table 10. Comparison between the numerical and exact solutions at t = 2, k = 0.002,
.
![]()
Figure 3. The exact and numerical results when the time t = 2.0 with k = 0.01.
![]()
Figure 4. The exact and numerical results when the timet = 5.0 with k = 0.01.
![]()
Table 11. The L∞ error for the numerical and exact solutions for a big time when k = 0.01,
from t = 15.0 to t = 50.0.
![]()
Figure 5. The exact and numerical results when the time t = 15.0 with k = 0.01.
![]()
Figure 6. The exact and numerical results when the time t = 25.0 with k = 0.01.
From Figures 5-9, we observe that the smaller the
(than the value of h), the better the accuracy. The numerical approximations are still acceptable within the large time.
The following figures, Figures 10-13, show the 3D representation of the numerical solutions of the dissipative equation for virus time and the same discretisations (h).
5. Conclusion
In this article, we discussed the non-polynomial spline method and the cubic
![]()
Figure 7. The exact and numerical results when the time t = 35.0 with k = 0.01.
![]()
Figure 8. The exact and numerical results when the time t = 45.0 with k = 0.01.
![]()
Figure 9. The exact and numerical results when the timet = 50.0 with k = 0.01.
![]()
Figure 10. 3D representation of the numerical solutions of the dissipative from the time t = 0.0 to t = 10.0.
![]()
Figure 11. 3D representation of the numerical solutions of the dissipative from the time t = 0.0 to 20.0.
B-spline method for solving a nonlinear dissipative wave equation and its truncation errors. The stability analysis of these methods was shown to be conditionally stable. Furthermore, the obtained approximate numerical solutions maintain good accuracy compared with the exact solutions, especially for small values.
![]()
Figure 12. 3D representation of the numerical solutions of the dissipative from the time t = 10.0 to t = 20.0.
![]()
Figure 13. 3D representation of the numerical solutions of the dissipative from the timet = 20.0 to t = 40.0.
The results obtained by [4] demonstrate that solving the nonlinear dissipative wave equation using the cubic B-spline method is more accurate than using the non-polynomial spline method. A large set of values was used to treat the nonlinear dissipative wave equation using the cubic B-spline method, and both 2D and 3D graph representations were provided. Our conclusion was that the non-polynomial spline method is more useful when the researcher wants to obtain the local truncation error, while the B-spline method is more accurate for solving nonlinear partial differential equations.