Explicit Algebraic Stress Model for Three-Dimensional Turbulent Buoyant Flows Derived Using Tensor Representation ()
1. Introduction
Previously, tensor representation theory has been used by So et al. (2002) Ref. [1], to derive an explicit algebraic stress model (EASM) for homogeneous turbulent buoyant shear flows. Two different approaches have been adopted: one based on the proposal of Gatski and Speziale (1993) Ref. [2], and another employed the more general approach of Junger and Gatski (1998) Ref. [3]. The starting point of their analysis is the normalized anisotropic Reynolds stress equation simplified assuming homogeneous equilibrium turbulence. Thus derived, the equation is quadratic in the anisotropic stress tensor
which is symmetric and traceless. Here, k = tii/2 is the turbulent kinetic energy,
is the kinematic Reynolds stress tensor, ui is the ith component of the fluctuating velocity and the overbar is used to denote ensemble average. The resulting equation is implicit in b. However, tensor representation theory can be used to render this equation explicit; thus allowing explicit algebraic stress models to be developed for buoyant shear flows.
Up to this point, the derivation is quite general because no assumptions have been made to limit the model for two-dimensional (2-D) flows. As for the assumptions of homogeneity and equilibrium, they were made to simplify the b equation so that it can be reduced to an algebraic equation. Gatski and Speziale (1993) Ref. [2], and Jongen and Gatski (1998) Ref. [3] also invoked these assumptions in their derivation of the non-buoyant EASM. In principle, the representation theory can be used to formulate the tensor representation for b if the basis tensors chosen are traceless. For incompressible flows, the kinematic shear strain rate tensor
and the rotation rate tensor
are traceless. Since the buoyant flux tensor,
, that appears naturally in the b equation for buoyant flows is also traceless, it would appear that S, W and
could be used as basis tensors to form the tensor representation for b. Here,
is the buoyant production tensor, G = Gii/2 is the buoyant production of k, gi is the ith component of the gravitational vector, Ui is the ith component of the mean flow velocity vector, xi is the ith component of the space vector, θ is the fluctuating temperature, β is the coefficient of thermal expansion of the fluid and δij = 1 for i = j and 0 for
. The instantaneous velocity vector
and temperature
are decomposed into ensemble mean and fluctuating parts, i.e.,
and
.
If the assumption of 2-D flow were invoked, the properties of the tensors S, W and
will become quite different. While the tensors S and W become 2-D with elements in one row and one column being identically zero,
remains a 3-D tensor and its use to form the basis tensors for b with S and W becomes very complicated. Therefore, an assumption was made to split the buoyant flux tensor into two parts, a symmetric traceless tensor f = fij that has the same properties as S and W for 2-D homogeneous shear flows, and a three-dimensional tensor N = Nij. This was accomplished through the introduction of a 2-D tensor
, first proposed by Pope (1975) Ref. [4], to define
and
. The 2-D tensor
is defined as
. (1)
Thus partitioned, f has properties similar to that of S and W in the case of 2-D homogeneous shear flows, i.e., elements in one row and one column are identically zero, and the theoretical derivation of the EASM can be carried out to give an explicit expression for b.
The tensor representation thus proposed limits the applicability of the EASM to 2-D flows only. In the EASM derived by So et al. (2002) Ref. [1], a five-term representation was assumed. Among the five basis tensors, three involve S and W, while two involve S, W and f. It is the presence of these last two basis tensors that render the representation not applicable to 3-D flows. Therefore, the derived EASM needs further extension to 3-D flows. It is recognized that the limitation stems from the partitioning of
into f and N. Therefore, if the derived EASM is to be equally applicable to 3-D flows, a way has to be found so that
can be chosen as one of the tensors used to form the basis tensors. This suggests that the basis tensors should be formed from S, W and
.
The present paper is an extension of the model of So et al. (2002) Ref. [1] to 3-D flows. However, the analysis will invoke the incompressibility assumption because S and W will remain as traceless tensors even for 3-D flows. Instead of splitting
into a 2-D symmetric traceless tensor f and a 3-D tensor N, the present approach uses S, W and
as the basis tensors to formulate a representation for b. A seven-term representation was derived for the general 3-D case. For pure shear flows without buoyancy, the EASM reduces to the form proposed by Gatski and Speziale (1993) Ref [2], i.e. a three-term representation. The seven-term representation of b is simplified to a four-term representation involving S, W and
as basis tensors, and its performance is found to be essentially identical to the EASM of So et al. (2002) Ref. [1] for 2-D homogeneous buoyant shear flows with a five-term representation involving S, W and f as basis tensors.
2. Mathematical Formulation
The EASM of So et al. (2002) Ref. [1] was derived from the Reynolds stress equation assuming the validity of Boussinesq approximation and equilibrium turbulence. The governing equation of the Reynolds stress anisotropy tensor as given in So et al. (2002) Ref. [1] is
,(2)
where
and
is the anisotropic dissipation rate tensor. In Equation (2),
,
,
,
,
,
,
,
, and
. The model constants are specified as
,
,
,
,
,
and
. Also,
is the shear production of k, e is the dissipation rate of k, and
is the shear stress production tensor. Equation (2) is implicit in b and further derivation is needed to render it explicit. In deriving Equation (2), the pressure-strain model of Speziale et al. (1991) Ref. [5] has been assumed. It can be written here as:
(3)
Following the work of Rivlin and Ericksen (1955) Ref. [6], let
be any symmetric 3 ´ 3 traceless tensors formed from the tensors S, W and
. A linear relation of the form,
, (4)
can be established between b and the tensors
, which are not necessarily linearly independent. With b being a function of S, W and
, there will be 41 tensors forming this basis altogether. According to Jongen and Gatski (1998) Ref. [3], for pure shear flows, three of the basis tensors are sufficient to give a relatively good approximation for 3-D flows. In view of this, a seven-term representation for b with four terms involving
is assumed in the present analysis. These seven basis tensors are given by
(5)
Assuming dij= 0 and a4= 0 and forming the scalar product of Equation (2) with each of the tensors
, and using (4), the following equation is obtained,
(6)
The above equation can be written in a compact form as,
. (7)
where
and (R, T(m)) are given by,
, (8a)
. (8b)
The solution of (7) can be obtained by determining the matrices (T(n)S, T(m)), (T(n)W, T(m)), (T(n), T(m)) and (R, T(m)). Here, a distinction can be made depending on whether the solution is sought for 2-D or 3-D flow. In the following, two different solutions are presented: one for 3-D flows with a 7-term basis and another for 2-D and 3-D flows with a 4-term basis. The 7-term representation gives rise to matrices that are very complicated, and it is not possible to simplify them to give analytical expressions for the coefficients Qn. The choice of a 4-term representation, on the other hand, allows simplifications to be made to deduce analytical expressions for Qn, and yet permits b to reduce to the buoyant case without shear identically. That way, the solution can be compared with the 5-term representation previously derived by So et al. (2002) Ref. [1] with S, W and f as the basis tensors.
3. Solution with a 7-Term Basis
According to Clapham and Nicholson (2009) Ref. [7], in linear algebra, the Cayley-Hamilton theorem states that every square matrix over a commutative ring satisfies its own characteristic equation. In view of this property, it is helpful to invoke the Cayley-Hamilton theorem in the present analysis. Therefore, using the Cayley-Hamilton theorem identity for their entries, the matrices (T(n)S, T(m)), (T(n)W, T(m)), (T(n), T(m)) and (R, T(m)) can be reduced to:
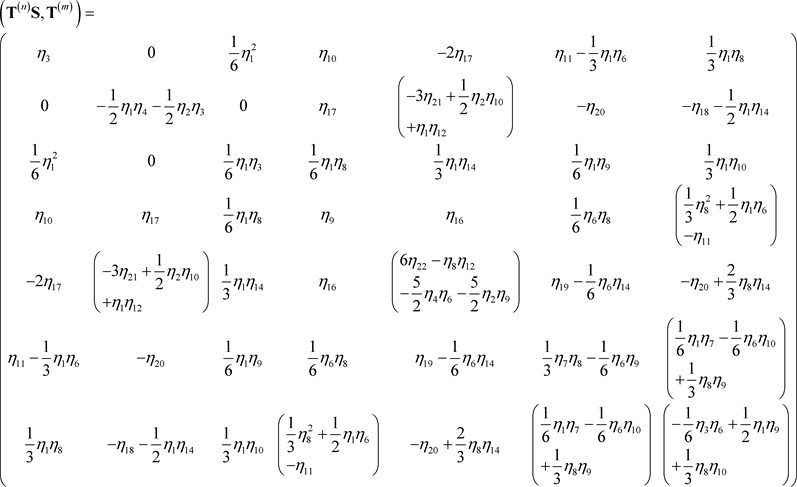 (9a)
(9a)
 (9b)
(9b)
, (9c)
, (9d)
where the scalar invariants hi’s are given by
(10)
Matrix A(7) in Equation (8a), its inverse, and the scalar coefficients of Equation (4) are deduced by making use of the MAPLE software. The coefficients thus determined will allow Equation (4) to reduce correctly to the pure shear flow limit when
is set to zero and the pure buoyant flow limit when S and W vanish in Equation (2).
4. Solution with a 4-Term Basis
In the case of a 4-term representation, solution can be sought depending on whether 2-D or 3-D flows are considered. For 3-D flows, only the first four rows and columns of Equation (9) have to be retained and no further simplifications to the scalar coefficients hi can be made. On the other hand, for 2-D flows, the 4 * 4 matrices thus obtained are reduced to simpler forms as some of the hi’s from Equation (10) in this case simplify to
(11)
while others are as given in Equation (10). Thus simplified, the matrices, (T(n), T(m)), (R, T(m)), (T(n)S, T(m)) and (T(n)W, T(m)), in the 2-D case become
, (12a)
, (12b)
, (12c)
. (12d)
The matrix A(4) in the 2-D case is reduced to
, (13)
The inverse of A(4) and the scalar coefficients in this case are again obtained using the MAPLE software and the resultant coefficients Q1 to Q4 can be simplified to
, (14a)
, (14b)
, (14c)
, (14d)
where
, (15a)
, (15b)
and Q12, Q22, Q32 and Q42 are given in Appendix I.
Once derived, b depends on
, λ,
, and G. A model for
is required if
is to be evaluated. In So et al. (2002) Ref. [1],
was evaluated by solving its transport equation with a suitable model for the pressure scrambling term and the modeled transport equations for
and
, the temperature variance and its dissipation rate. The variable λ can be determined by solving the modeled transport equations for k and ε. Therefore,
, G and λ are all known, and the only unknown left is
. An equation for
can be derived following the approach taken in So et al. (2002) Ref. [1]. Again, the equation is found to be cubic, and it can be written as
, (16)
, (17a)
, (17b)
(17c)
Details of the derivation of Equation (16) are given in So et al. (2002) Ref. [1]. Since the roots of a cubic equation can be found in any mathematical handbook, such as Ref. [7], they are not given here. If b is to be explicitly determined, the heat flux model of So et al. (2002) Ref. [1] can again be adopted.
5. Discussion
The results given in Equation (4), Equation (14) and Equation (15) reduce to the pure shear flow and the pure buoyant flow limit when
and S are set to zero individually. When
is set to zero, Equation (4) yields a 3-term representation with Q4 = 0. The other scalar coefficients reduce to
,
and
, which are the same as those given by Gatski and Speziale (1993) Ref. [2] and Jongen and Gatski (1998) Ref. [3]. Furthermore, when Equation (4), Equation (14) and Equation (15) are substituted into Equation (2), the equation is satisfied identically. As for the pure buoyant limit, setting S to zero reduces Equation (4) to a 1-term representation and the result is given by
, because W is also zero. This is identical to the expression obtained from Equation (2) when S = W = 0 is substituted. In other words, Equation (4), Equation (14) and Equation (15) reduce to the two limiting forms correctly. Therefore, it remains to be shown that when Equation (4), Equation (14) and Equation (15) are used to calculate 2-D homogeneous buoyant shear flows the results are essentially identical to those given previously by So et al. (2002) Ref. [1].
The EASM previously derived by So et al. (2002) Ref. [1] and denoted as EASM/GS or EASM/BJG, has been validated against the direct numerical simulation (DNS) data of Gerz et al. (1989) Ref. [8] and also against calculations using a two-equation turbulence model, i.e., an EASM without accounting for buoyancy effects and a full Reynolds stress model assuming the SSG model of Speziale et al. 1991 Ref. [5] for the pressure strain term. Since EASM/GS and EASM/BJG give identical results, from this point on, the model of So et al. (2002) Ref. [1] will be referred to as EASM/BJG. This comparison reveals that, while accounting for buoyancy effects is important in an EASM, the full Reynolds stress model gives the best prediction of the DNS data because of its ability to model the history of the flow. The present EASM, denoted as EASM/Γ, is essentially a more general version of EASM/BJG. Therefore, its validity can be verified by comparing with the calculations of EASM/BJG and the DNS data. Calculated results from the two-equation and the Reynolds stress model will not be
![]()
Figure 1. Comparison of the calculated k with DNS data. (a) is for the Ri = 0.1 case, and (b) is for the Ri = 1.0 case.
shown because they have already been compared to EASM/BJG in So et al. (2002) Ref. [1]. The details of the calculations, including the assumption and the normalization used to reduce the governing equations to ordinary differential equations, the numerical method, and the specification of the initial conditions for the Gerz et al. (1989) Ref. [8] case, have been fully discussed in So et al. (2002) Ref. [1]. These details will not be repeated here, the interested readers could consult the reference. Calculations have been carried out for a range of Richardson numbers ranging from
to 1.0.
![]()
Figure 2. Comparison of the calculated temperature variance with DNS data. (a) is for the Ri = 0.1 case, and (b) is for the Ri = 1.0 case.
Here, S = dU/dz is the shear gradient, dΘ/dz is the temperature gradient, gc is the gravitational constant and z is the vertical coordinate aligned with the gravitational direction g3.
The plots k/ko,
,
and
versus τ = St are shown in Figures 1-4, respectively. The subscript “o” is used here to denote the initial value and τ is the dimensionless time. Here, the prime is used to denote the root mean square value of the fluctuating quantities. Only the results for Ri = 0.1 and
![]()
Figure 3. Comparison of the calculated streamwise heat flux with DNS data. (a) is for the Ri = 0.1 case, and (b) is for the Ri = 1.0 case.
![]()
Figure 4. Comparison of the calculated normal heat flux with DNS data. (a) is for the Ri = 0.1 case, and (b) is for the Ri = 1.0 case.
1.0 are shown in Figures 1-4. Essentially the same predicted behavior is seen for other values of Ri. The predictions of EASM/BJG and EASM/Γ are essentially identical, thus showing that a one-term explicit representation of the buoyant flux is sufficient to describe the buoyant behavior as that given by a 2-term representation. Therefore, partitioning of
into f and N is restrictive. It is demonstrated here that such a partitioning is not necessary. As a result, a fairly general form of EASM for turbulent buoyant shear flows has been derived. The resulting EASM is valid for both 2-D and 3-D flows.
6. Conclusion
This paper shows a more general way to derive an EASM for 3-D buoyant shear flows. The approach reveals that it is not necessary to partition the buoyant flux tensor into a 2-D symmetric traceless tensor f and a 3-D tensor N to deduce analytical expressions for the coefficients of the representation for b. The derivation can be carried out directly using
, even though
is a symmetric traceless 3-D tensor. Thus, the methodology established here can serve as a general approach to derive EASM for a variety of flows where external body forces give rise to a symmetric traceless 3-D tensor in the b equation.
Acknowledgements
The author wishes to acknowledge support given him by the Mechanical Engineering Department, The Hong Kong Polytechnic University, through administrative help, and library and computing services.
Appendix