1. Introduction
There are mainly two types of market systems, one is Monopoly and the other is Perfect Competition and they are completely contrary to each other in character [1] [2]. Cournot proposed a new market system named Oligopoly [3]. Oligopoly is the transitional case of monopoly and perfect competition [4] [5]. Duopoly is the sub-case of oligopoly. A duopoly is a market system that is controlled by two firms. There are two classical models in the theory of duopoly. One is of Cournot and the other is of Bertrand [6]. Both mentioned models firms were generating the same kind of goods and adopting homogeneous strategies. Cournot model firms use quantity strategies while Bertrand model firms use price strategies [7] [8]. Numerous researchers have established mathematical models to deal with diverse situations of duopoly [9] [10]. In most established studies, researchers assumed that in a duopoly, both firms produce homogeneous goods and adopt the same kind of strategy either quantity strategy or price strategy [11] [12]. But in real-life situations, firms may produce different kinds of products which provide customers a variety of goods to choose from them and it provides opportunities for firms to improve their products because of competition. Also, it is not necessary that both firms adopt homogeneous strategies [13]. Instead, in order to get maximum benefit and avail market situations, firms use different strategies. Various studies have been conducted to give a realistic outlook to the classical model [14] [15]. Many theories are established on the idea of product differentiation [16] [17] as well. Some researchers established the relation between relative profit objective and the advertising competition model [18] [19]. But, there is not abundant work on the non-linear duopoly model with the heterogeneous cost of production and heterogeneous strategies. In this paper, the strategic behavior in a heterogeneous nonlinear differentiated duopoly is observed. For this, a duopoly model is examined after introducing nonlinearity through heterogeneous strategies and differentiated goods while the cost of production of both firms is also heterogeneous. The main objective of the paper is to analyze the static effect of non-linearity on the behavior of the competitors. Non-linearity in the duopoly model is due to various reasons like heterogeneity in production cost, heterogeneity in strategy, and heterogeneity in competition, which means that different firms choose different strategies. This paper is systematized like this: In Section 2, there is an outline of the general demand function in dissimilar duopoly; Section 3 describes the differentiated duopoly with linear demand function; Section 4 explains the duopoly with non-linear demand with heterogeneous stratagems as well as heterogeneous manufacturing cost and a conclusion is given in Section 5.
2. Duopoly with General Demand Function
As in a duopoly, two firms compete against each other. So, let there be two firms firm 1 and firm 2. Let us suppose that firm 1 produces
quantity of a product with price
and firm 2 produces
quantity of product with price
. The motive of both firms is to earn maximum profit. Let us consider the case when both players follow heterogeneous strategy. In that case, one of the players follows quantity strategy taking price variable of other as given and other follows price strategy taking quantity variable of other firm as given. In other words, one of the players follows Cournot and the other Bertrand. From here forth, we write CB competition, if the first player follows Cournot and second Bertrand competition. Similarly, BC competition indicates that the first firm follows Bertrand competition and the other Cournot. The inverse demand function [20] is given by
Above equation can also be written as
(2.1)
(2.2)
If
and
are marginal production costs of firm 1 and firm 2 respectively, their corresponding profits are
(2.3)
(2.4)
In CB competition, firm 1 is quantity setter and firm 2 is price setter. So, variables are
and
. Therefore, rewriting Equations (2.3) and (2.4), we get
and
Thus, profit in CB competition of both the firms is a function of two variables, where quantity is variable for the first firm and price for the second firm, as both the firms want to earn maximum profit. For that take partial derivatives of these profit functions w.r.t
and
respectively and then equate to zero. Reaction functions are obtained by solving these equations for value of
and
for which profit is maximum. Moreover, these values of
and
give CB equilibrium [20]. Similarly, in BC competition, firm 1 is the price setter and firm 2 is quantity setter. Value of
is substituted in Equations (2.3) and (2.4) respectively as follows:
and
As discussed above, take partial derivatives of these profit functions w.r.t.
and
respectively and then equate to zero. Reaction functions are obtained by solving these equations for values of
and
for which profit is maximum. Moreover, these values of
and
give BC equilibrium.
3. Differentiated Duopoly Model with Linear Demand Function
Here we consider that both the firms are dealing in differentiated goods. Let
be the measure of extent to which product of both firms differentiate. Linear inverse demand function is given by
(3.1)
(3.2)
where
denotes the maximum price firms want to gain,
means that goods are perfect substitutes and
means independent products. Here we take assumption that
[21]. Now we want to find CB equilibrium and maximum profits of both the firms. So, we need to find the values of
and
from Equations (3.1) and (3.2). For this multiply Equation (3.2) by
and subtract from (3.1), which gives
(3.3)
Similarly, Multiplying (3.1) by
and subtract from (3.2), which gives
(3.4)
As in CB competition
and
are the variables. So, eliminate
from Equations (3.1) by substituting value of
from (3.2)
(3.5)
(3.6)
by using Equation (3.5), Equation (3.6) reduces to
(3.7)
Also, by using Equation (2.4), we have
Further, using Equation (3.4), we get
Substituting value of
from Equation (3.5) in
, we get
(3.8)
Now from Equations (3.7) and (3.8), it is clear that
and
are functions of variables
and
. So, reactions functions can be obtained by taking
and
we get
(3.9)
(3.10)
If we consider the case that production cost of both firms is positive and same i.e. homogeneous production cost. Take
and
both zero, and this is typical postulation of linear models. Solving reaction functions given in Equations (3.9) and (3.10) simultaneously, we get equilibrium output in CB competition.
(3.11)
Substituting this value of
in Equation (3.11), we get
(3.12)
Now we need to find
and
, for that substitute value of
and
from (3.11) and (3.12) in Equation (3.5), which is
(3.13)
Then we get
(3.14)
Next for value of
, use values of (3.12) and (3.13) in Equation (3.4), so that
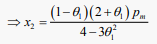 (3.15)
(3.15)
So, CB competition Equations (3.11) and (3.14) give equilibrium output and Equations (3.12) and (3.13) give equilibrium price. Substitute these values in profit function to get CB profit
and
of both the firms respectively. When we take the ratio of the output, prices and profit of both the firms, then observations are as follows:
and
Similarly, in BC competition, the case is reversed only. In this case, firm 1 is price setter and takes price as variable considering output of the other is given and firm 2 is quantity setter, takes quantity as variable considering price of other as given. So, we need to just replace
by
and
by
in the above drawn results. Then observations are as follows:
Above observations clearly indicate that in both CB and BC competition, out of two firms producing differentiated goods and following heterogeneous strategy, the quantity setter firm produces more output, have fewer prices and enjoys more profits.
4. Duopoly Model with Non-Linear Demand
Here we take an assumption that demand is iso-elastic [22]. Then inverse non-linear demand function is given by
and
(4.1)
and
(4.2)
Solve these equations for the output of firms
and
Then
(4.3)
and
(4.4)
In CB competition with non-linear demand function, reaction functions will be obtained as in case of linear demand functions. We will get CB reaction functions for firm 1 and firm 2 as
(4.5)
(4.6)
Here reactions functions are function of two variables
and
as mentioned above. But for sake of convenience, convert the reaction functions in variables
and
, and substitute the value of
in Equation (4.5), we get
(4.7)
Similarly, we get
(4.8)
Dividing (4.7) by (4.8)
Take
and
, Then
(4.9)
Let the right hand side of Equation (4.9) be denoted by
and left hand side be denoted by
. Let the solution of Equation (4.9) be denoted by Y. So, intersection of
and
gives CB equilibrium.
(4.10)
In order to express the value of CB output in terms of Y. Use (4.7) to get
Also from (4.8)
(4.11)
Similarly
(4.12)
Also express prices and profits of both the firms in terms of parameter Y so that it can be compared. For this substitute values of
and
in
and
to get
(4.13)
Similarly
(4.14)
Now, profit in CB equilibrium of firm 1 is
In the similar way
Taking ratio of output, prices and profits of both the firms, we get
(4.15)
From (4.9) and (4.10), it is clear that
Now
According as
or
,
, and considering
, we get a critical value of production cost ratio
. Let this value be denoted by
, then
As mentioned above, If
,
. So, from Equation (4.9), it is obtained that
Similarly, for
,
. Then, Equation (4.9) gives
So,
, <1, =1 or >1 And
or
According as
or
.
This means that the parameter region
has two sub-regions, below and above the curve
.
and
for
in the region above the curve.
and
below the curve
. This can be interpreted that whichever firm produces more output sells at lower prices.
Bertrand Cournot Competitions
In BC competition, firm 1 is the price setter and the second is quantity setter. Following the above stated procedure, the reaction functions are
(4.16)
(4.17)
The reaction functions given in above equations are defined in
space. BC equilibrium will be converted in quantity space
by substituting values of
in these equations. Equation (4.16) becomes
(4.18)
Similarly, Equation (4.17) becomes
i.e.
(4.19)
Equations (4.18) and (4.19) are defined in
space. Dividing (4.18) and (4.19) gives
Taking
, above equation becomes,
(4.20)
Right hand side of Equation (4.20) and Equation (4.9) is the same.
As above, denote right hand side by
and left hand side by
. Solution of Equation (4.20) will be given by intersection of these two functions.
This solution is BC equilibrium.
Since
is monotonically increasing and
. So,
is bounded above. Also,
.
Here,
.
This is equivalent to
.
So, here conjecture is
.
Let roots of Equation (4.20) be denoted by Z, which is a function of
and
.
(4.21)
Substituting
and
in Equations (4.18) and (4.19), in order to get explicit form of BC output in terms of parameters. Then
(4.22)
and for finding value of
, take
in Equations (4.18) and (4.19).
(4.23)
Substituting values of
and
from Equations (4.22) and (4.23) in equations
BC prices are
Their ratios are
(4.24)
As mentioned above,
, this will give a critical value of production cost ratio, denote it by
. From expression (4.20), using
, it is obtained that
.
If
i.e.
From Equation (4.21), it is clear that
i.e.
i.e.
i.e.
Similarly, for
,
,
.
This means output of firm 1 is more than that of firm 2, and its prices are lesser above the critical line
. But in the region below the critical line, firm 2 produces more output than the firm 1 and set lower prices.
When repeating the above procedure, we reach the conclusion that efficient firm produces more output and sells at lower price. Here efficient means production cost is less.
5. Conclusions
In a duopoly market system when both firms choose heterogeneous strategies i.e. one of the firms chooses quantity strategies and the other chooses price strategies, it is observed that when production costs are homogeneous, then quantity setter firms produce more output, face lower prices, and make larger profits than price setter firm. So, the quantity strategy is more profitable. When strategies and production costs are heterogeneous, the efficiency of the firms is the determining factor to decide which firm will produce more and sell at a lower price.
This paper studies the static aspects of the non-linear heterogeneous duopoly model. There is a future scope for investigating the dynamical aspects with numerical simulation.