1. Introduction
Hilbert (David Hilbert, 希尔伯特, 1862-1943 a.d) is a well-known German mathematician. He was born in East Prussia Konigsberg. Since 1895, in University of Goettingen, is the life tenure of professor, becoming a member of the royal society in 1928. In general, he in geometry and mathematics on the basis of the profound study is the most famous; Hilbert’s Programme prompted Computability Theory.
He collected 23 problems, now known as Hilbert’s Problems, the process of twentieth century mathematics development had a profound impact; among them, there are still many problems unsolved.
His achievements include the Hilbert basal Theorem of ring theory (Hilbert’s Basis Theorem), the geometry Basis (Grundlagen der Geometrie), and Hilbert Space and other theory research.
The Hilbert, a German mathematician, into the basic algebraic invariant, algebraic number theory, geometry, variational method, the Hilbert space, etc., have a great contribution, was the greatest mathematician of his time.
He advocated mathematical axiomatization, and put forward “Hilbert 23 problems”, promoting the 20th century development of mathematics.
1.1. Mathematical Contribution
In 1862, Hilbert was born in Konigsberg (at that time, as the capital of east Prussia, drawing into the Russian territory) world war ii, in 1880 into the local university, a doctorate in 1884, 1886 teaching in the university, become a professor and married in 1892. In 1895 became a professor at the University of Goettingen, until death.
Each period Hilbert math characteristic is only focused on one area, the main problem to solve, and turned to another area.
From 1884 to 1892, which focuses on the Hilbert algebraic invariants, proves that any transformation group of algebraic expression invariant, has a limited set of basement, and can actually be constructed.
From 1892 to 1898, focusing on algebraic number theory, laid the foundation of theory of the class body. In 1898 began to focus on the problem of surface geometry axiomatic, results in the next year to complete, author, the basis of geometry for plane geometry axiomatic system is established.
From 1899 to 1901 is the period of variational method, the Hilbert with strict proof, and established the Dirichlet principle: under the boundary curve and boundary value slightly limitation, for several consecutive partial derivatives of the given boundary value and all the possible function, there will be a function of double integral value reaches the minimum.
In 1902, the Hilbert turned to integral equations, the corresponding infinite dimensional linear space (Hilbert space), for the subsequent quantum physics reserves the sharp mathematical tools.
Besides in various fields have outstanding achievements, the Hilbert geometry axiomatic strict ideas soon spread to mathematics in various fields, and Hilbert himself also seriously studied physics, to all branches of physics axiomatic; But his achievements in physics axiomatization are limited.
In 1922, the Hilbert axiomatic itself to research, hope to prove that the axiomatic system of the general in independence, consistency and completeness is not a problem. But in the 1930s, GöDel’s few papers make this hope fail to be fully implemented.
In addition, the Hilbert Paris in 1900, the 2nd international conference on mathematical speech also deeply affect the development of 20th century mathematics. He says the problem is a fountain of mathematics activities, and some problems from the experience and natural phenomena, because others will do a study of logic integration, generalization and specialization. The theory and experience of interaction make mathematics is very useful. He in the name of “math” and a half after the speech, cites the 23 to the twentieth century mathematicians to solve problems, to illustrate the background one by one. These are the famous Hilbert 23 problems, they did in the 20th century an important role in the development of mathematics.
Hilbert made it for knowledge has always been optimistic, corresponding to the philosopher du Bois-Reymond pessimistic view: we are ignorant, and I will have been ignorant, Hilbert presents a lifelong belief is: we have to know, we will know.
After the 70-year-old Hilbert’s body was not so good, memory loss. One day, Hasse and Hilbert about class body theory, the basic concept of the Hilbert has demanded the class body theory and results explain to him, then Hilbert’s reaction was: this is really beautiful, is who invented?
Hitler came to power in 1933, began to persecute jews, the old disciple of Hilbert left Germany. The Hilbert became alone, with no energy, to drag the rest.
1.2. Hilbert 23 Problems
Hilbert (Hilbert d., 1862.1.23-1943.2.14) is the 20th century one of the greatest mathematicians in Germany and the world. He runs across two centuries of 60 years of research career, through nearly all of the modern mathematics forefront, and his thoughts are deeply penetrating into the whole of modern mathematics. Hilbert is the core of the Gottingen school, with his hard work and sincere personal qualities attracted youth researchers scholars from around the world, make Gottingen traditional influence in the world. Hilbert died, published in the journal nature, Germany the view that is rare in the world have a mathematician work, originated from Hilbert’s work is not in some way. He likes maths world Alexander, in the whole map of mathematics, left his glorious name. Conference in Paris in 1900, Hilbert mathematicians introduced 23 of the most important problem for the twentieth century mathematicians to study, this is the famous “Hilbert 23 problems”.
In 1975, the University of Illinois in the United States at a meeting of the international mathematics, mathematicians three-quarters of a century are reviewed the research progress of Hilbert 23 issues. At that time, about half of the problem has been solved, the remaining half of most also have significant progress.
Mathematicians in the United States, in 1976, the selection of the United States since 1940 in ten big achievements of mathematics, three is the Hilbert 1, 5, 10 the solution of the problem. Therefore, to solve the problem of Hilbert, contemporary mathematician is considered a great honour.
The following excerpt is published in 1987, “the mathematician small dictionary” and some other literature collection of Hilbert 23 issues:
1) The continuum hypothesis
Cantor (康托, 1874) speculation in a countable set between the base and the base of real Numbers is no other base, this is the famous continuum hypothesis.
Godel (哥德尔, 1938) proved the continuum hypothesis and the universally recognized Merlot-Frenkel (策梅洛·弗伦克尔) axiomatic set theory system of no contradiction.
American mathematician Cohen (科亨, 1963) proved that continuous assumption and Merlot-Frenkel (策梅洛·弗伦克尔) axiomatic set theory were independent of each other.
Continuum hypothesis, therefore, cannot be inside of Merlot-Frenkel (策梅洛·弗伦克尔) axiom system to prove its correctness or not. Hilbert problem 1 in this sense has been resolved.
2) The compatibility of arithmetic axiom
The compatibility of Euclidean (欧几里得) geometry boils down to the compatibility of axiom at arithmetic.
Hilbert had formalism plan proof theory method is put forward to prove it. Godel (哥德尔, 1931) publishing the incompleteness theorem denied this view.
German mathematician Genc (根茨, 1936), under the condition of using transfinite induction, proved arithmetic axiom of compatibility.
Published in 1988, the “China encyclopedia” mathematics, points out that mathematical compatibility problems are unresolved.
3) The two bottom contour, such as the volume of a tetrahedron is equal
Question means, there are two equilateral tetrahedron contours, they cannot be decomposed into a finite number of small tetrahedron, make the two groups of tetrahedron congruent to each other.
Dern (德恩, 1990) was to give a positive answer to this question.
4) The distance in a straight line between two points is the most short term problem
This question is too general. Meet the geometry of the nature of many, and therefore need to increase some constraints.
Soviet union mathematician Pogorelov (波格列洛夫, 1973) announced that in the case of symmetric distance, problem solved.
“China encyclopedia”, said after Hilbert, in terms of structure and discusses various special metric geometry has a lot of progress, but the problem is not solved.
5) The concept of Lie (李) group, the definition of a continuous transformation of the functions of this group of don’t assume that is differentiable
The problem referred to as the analyticity of continuous group, namely: whether every local Euclidean (欧几里得) group there must be a Lie (李) group?
Soviet union mathematicians Neumann (冯·诺伊曼, 1933) for a compact group, Bonderyagin (邦德里雅金, 1951) for a group of exchange, and Xie (谢瓦荚, 1941) for the solvable group obtained the positive answer of this problem.
Gleason (格利森, 1952), Montgomery (蒙哥马利, 1952) and Zippin (齐宾, 1852) solving together, completely positive results were obtained.
6) The axiomatization of physics
Hilbert suggests using mathematical method of axiomatic push all physical performance, the first is the probability and mechanics.
Soviet union mathematician Kolmogorov (柯尔莫哥洛夫, 1933) implemented the axiomatization of probability theory.
Later, in quantum mechanics, quantum field theory has achieved great success.
But whether physics can come axiomatization, many people doubt it.
7) The number of some irrational and transcendence
For any algebraic number of alpha indicates, it is to prove the irrational and transcendence. For any algebraic number of alpha indicates and for any irrational algebraic number of beta indicates, it is to prove the alpha beta of transcendence.
Gelfand (A.O. 盖尔方德, 1934) and Schneider (T. 施奈德, 1934) independently solved the second part of the problem, namely, for any algebraic number of alpha indicates in which alpha is not equal to 0 or 1, and for any irrational algebra of beta indicates, it can be to prove the alpha beta of transcendence.
8) A prime number
There are a lot of problems, including the Riemann (黎曼) hypothesis, Goldbach (哥德巴赫) conjecture, and problem of twin prime Numbers.
In general the Riemann (黎曼) hypothesis is still to be solved.
For Goldbach (哥德巴赫) conjecture, the best result belongs to the trained Chen (陈景润, 1966), but is distance from the most to solve themselves.
The best results of the problem of the prime twins are trained by Chen (陈景润), Tao (陶哲轩), Zhang (张益唐) and others. Zhang (张益唐) proved that there is an infinite number difference of the prime Numbers less than 70 million.
9) In any number of domains has proved the most general reciprocity law
The issue was given a positive answer by Japanese mathematician Takagi (高木贞治, 1921) and German mathematician Atin (阿廷1927).
10) The solvability of Diophantine (丢番图) equations
The solvability of Diophantine (丢番图) equation is able to calculate the integer root of an integer coefficient equation.
Hilbert asked, can use a general algorithm composed of limited steps to judge a solvability of diophantine equation?
Soviet union mathematician Matiyasevich (IO.B. 马季亚谢维奇, 1933) proved that the Hilbert’s desired algorithm does not exist.
11) A coefficient for arbitrary quadratic algebraic number
Hasse (H. 哈塞, 1929) and Siegel (C.L. 西格尔, 1936, 1951) were to obtain important results on this issue.
12) Crocker (克罗克) theorem to Abel (阿贝尔) domains to any rational domain algebra
This problem only some sporadic results, is far from solved also differ.
13) With only two variables function solution of the general equation of seven times
With only two variables function solution of the general equation of seven times seven equation root depends on three parameters a, b, c, namely x = x (a, b, c). This function can be expressed in binary function?
Soviet union mathematician Arnold (阿诺尔德, 1957) solved the continuous function.
Soviet union mathematician Weissjin (维士斯金, 1964) put it to the situation continuously differentiable function.
But if the requirement is analytic function, the problem hasn’t been solved yet.
14) Prove that certain types of complete function are limited
Prove that certain types of complete function of the finiteness of the algebraic invariant and problems.
An counter example was given by Japanese mathematician Nagata (永田雅宜, 1958).
15) Schubert (舒伯特) count calculus based strictly
Schubert (舒伯特) count strict basic problem is a typical calculus: there are four lines in three dimensional space, can ask a few lines and the four lines intersect?
An intuitive method was presented by Schubert (舒伯特).
Hilbert called for the problem of generalization and give strict basis.
Having some computable method, it and algebraic geometry are not closely related.
But has yet to establish the basis of strict.
16) The algebraic curve and algebraic curve surface topology
The problem is classified into two parts. First part involves an algebra curve containing the maximum number of branch of the closed curve. Later asked to discuss the maximum number of limit cycles and the relative position of the X, Y is X,Y, n polynomial.
Soviet union mathematician Piotrowski (彼得罗夫斯基), declared the limit cycle number of when n = 2 is not more than 3, but this is wrong, have been elaborated by the Chinese mathematicians to cite the counter example in 1979.
17) The sum of the squares of the other forms of positive semidefinite expression
The sum of the squares of the other forms of positive semidefinite said that if a real coefficient polynomial n yuan for all arrays (x1, x2, ..., xn) are constant is greater than or equal to 0, whether can be written in the form of sum of squares?
German mathematician Artin (阿廷, 1927) testified that this is right.
18) Use congruent polyhedral structure space
Using congruent polyhedral structure space, German mathematicians BobMach (比勃马赫, 1910) and Podbyhart (荚因哈特, 1928) made a part of the solution.
19) The regular solution of variational problem whether certain parsing
The regular solution of variational problem whether certain analytic very few studies on this issue.
Some results were drawn by Soviet union mathematicians Bernstein (C.H. 伯恩斯坦) and Piotrowski (彼得罗夫斯基), etc.
20) General boundary value problem
Advances in general boundary value problem for this issue very quickly, has become a big branch of mathematics. Continue to study.
21) Have to order value of the existence of the solution of the linear differential equation
Having to order value of the existence of the solution of the linear differential equation has been given by German mathematicians Hilbert (希尔伯特, 1905), and Oral (H. 罗尔, 1957) solution work.
22) The composed of automorphic functions uniformization of analytic function
Composed of self-controlled function analytical function of uniformization involves the hardships of the Riemann (黎曼) surface.
Krupp (P. 克伯, 1907) won the important breakthrough, other aspects haven’t been solved yet.
23) The further development of the variational method
The variational method to further develop is not a math problem, just talked about general attitudes towards the variational method.
Since the 20th century variational method had the very big development.
The 23 question involves the most important areas of modern mathematics, to promote the development of mathematics in the twentieth century.
For Hilbert’s sixth mathematical conjecture, in addition, many scholars tried to use the Chinese theory of Yin and Yang to establish an axiomatic system in west. These scholars are including Zhang (2009), Aucher (2015), Zhang & Zhang (2004), Zhang et al. (2016), Zhang (2002), Zhang (1998), Chen et al. (2014), Zhang & Kandel (2012), Fang (2012), Kim et al. (2014), Fang & Faure (2011), and so on. Also some scholars, for example, Zhang & Chen (2009), tried to use the concept of Yin Yang Wu Xing in Traditional Chinese Philosophy (TCP) or Traditional Chinese Mathematics (TCMath) to improve the axiomatic system in west. However, in this paper, to explain is: mathematics of trying to cannot be completely successful, could only partial success. The kernel of this paper is the existence and reasoning of the incompatibility relations, and it accords with the oriental or eastern thinking model.
In fact, at present a lot of many concepts in TCP or TCMath have been accepted by many scholars. In TCP or TCMath, for example, there is a very important concept—Chi or Qi as energy of the system, which is partially accepted by Hilbert as Hilbert manifolds to be studied by many mathematical researchers. The Burghelea & Kuiper (1969) and Ruelle (1982) are the most prominent. It is because they are all to identify the change problem of any input variables for any output variables but don’t worry about the contents of the variable.
The philosophical meaning of five aspects of non-authigenic logic is an important concept of TCP or TCMath. And it is necessary to discuss the five basic principles and their rules of non-authigenic logic. According to the Yin Yang Wu Xing philosophical meaning, it is known that the world of logic should have the meaning of the five aspects. That is to say: taking the research object is classified into five categories, i.e., obtaining image from classification or classification taking image (比类取象), to achieve real purpose of learning about the world.
Zhang (1993, 2006, 2007a, 2007b, 2011a, 2011b, 2012, 2018a, 2018b 2020) has started a great interest and admired works for TCP or TCMath, where, through mathematical reasoning, they demonstrate the presence of incompatibility relations, which are predominant in daily life, yet absent in traditional Aristotelian Western logic.
The main issue to be researched shall be led in a more direct way. The problem of logic is the key to all issues. The non-authigenic logic or the authigenic logic is the main logic of eastern culture, or western culture, respectively. The philosophical meaning of five aspects of non-authigenic logic can be used to TCP itself. The main frame in a more direct way of TCP includes the non-authigenic logic (不自生逻辑) as the no Axiom system, the loving analysis (相生分析) as the preconception principle, the killing analysis (相克分析) as the integration coordination combination principle, the killing reproducibility (相克再现性) as the logic layering principle and the loving reproducibility (相生再现性) as the automation principle. The paper mainly demonstrates the non-authigenic logic. Other questions will be dealt with separately.
Information of the theoretical basis shall be given in advance to lay foundation for following research. The non-authigenic thinking rule or the no Axiom system is the key to the non-authigenic logic, liking wood. The loving analysis is the preconception principle of the non-authigenic logic, liking fire. The killing analysis is the integration coordination combination principle of the non-authigenic logic, liking earth. The killing reproducibility is the logic layering principle of the non-authigenic logic, liking metal, And the loving reproducibility is the automation principle of the non-authigenic logic liking water. There are five philosophical bases of TCP.
Many people as Western persons are beyond all doubt that the Yin Yang Wu Xing theory is superior to the traditional true-false logic, which does not contemplate incompatibility relations, which Zhang & Shao (2012) have expertly explained from a mathematical standpoint.
The work Zhang (1993, 2007a) has started, allows many people like Western person to think of a true re-foundation of mathematical language, to make it a better suited tool for the needs of mankind mathematical complex system and the environment. Even so, Zhang & Shao (2012) also bring to light the difficulty of establishing the values of both the intervention reaction coefficients
and the self-protection coefficient
as parameters with due accuracy.
Latest works discovered the academic relationships between Leibnitz and Jesuit priest J. Bouvet, linking the deduction of the Trigrams to German binary system situation that coincidentally appears in quoted paper. This will clearly realize the scientific-mathematical fundamentals of Traditional Chinese Medicine (TCM, see Contributions).
There are some publications Inchauspe, (2014, 2015a, 2015b, 2017), Inchauspe & Inchauspe (2019) and Inchauspe & Tachini (2020), devoted to demonstrate in Occident the exact basis of Chinese Medicine, i.e. as Chinese Five Elements find precise consistency with Euclid’s Five Regular Polyhedra, as well as the trigrammatic order of the I-Ching hexagrams.
The article proceeds as follows. Section 2 contains the basic generalized relations, generalized reasoning and steady multilateral systems of non-authigenic logic. And a negative philosophical answer of Hilbert’s sixth mathematical conjecture is demonstrated in Section 3. And a negative mathematical answer of Hilbert’s sixth mathematical conjecture is demonstrated in Section 4. Referential significance of this study could be further enhanced in Section 5. And conclusions are drawn in Section 6.
2. Generalized Relations, Generalized Reasoning and Steady Multilateral Systems of Non-Authigenic Logic
2.1. Generalized Relations and Reasoning of Non-Authigenic Logic
Suppose all of the research objects are a collection
. The authigenic logic is first to look at the collection
by observation, and discovered some research objects which constitute of a sub-collection
, then according to the nature of the sub-set
of axioms and assumptions, and according to the assumption to judge a certain proposition true or false. If a logical reasoning is based on the observations as
, then the corresponding logic is called authigenic logic.
But the non-authigenic logic is not to look at the collection
of the research objects, just according to themselves needs, classification taking images corresponding to some group, put forward and want to know what is the relation between different classes of the research objects? If a logical reasoning has nothing to do with the collection
of the research objects, then the corresponding logic is called non-authigenic logic in Zhang (2018a).
From oriental or eastern philosophical thought, if a person will go to solve an objective problem of a mathematical complex system, and if this person can get some analysis conclusion only by using non-authigenic logical reasoning or analysis, then the analysis conclusion can ensure to conform to the objective facts and to be reproduced by all others because the logical reasoning has nothing to do with the collection
of the research objects. This property is known as the reproducibility.
Reproducibility is the fundamental meaning of balanced measurement if the real conclusion of objects cannot be known. In general, the reproducibility was defined in a stable environment. The same object is measured by a lot of operators and not only by using the similar measuring instruments and methods. But the measured values of average variation should be similar to each other, and should be similar to the objective facts. Reproducibility also refers to the average variation is smaller between measuring systems and measuring conditions.
Reproducibility is the most basic requirements for mathematical scholars. If there is no reproducibility, so there would be no classical in TCP. Because mathematical scholars are to use the data to study the science law behind the data, the law has nothing to do with mathematical scholars, and has nothing to do with how much data observed by mathematical scholars, and has nothing to do with how what reasonable methods used by mathematical scholars. The mathematical method is reasonable if the method can at least ensure the reproducibility of the mathematical analysis conclusion. As long as mathematical scholars using mathematical method have reproducibility, so the analysis of the conclusions should be unique based on similar data.
In mathematics, let
be a non-empty set (the collection
of the research objects). Then there is a non-empty Descartesian set
.
The non-empty subset
is called a relation of
. TCP mainly researches general relation rule for a general
rather than for a special subset
. So the general set
cannot be supposed. The thing can only be done to research the structure of the set of relations
because the structure has nothing to do with the collection
of the research objects and without considering the specific content of the research object.
For a relation set
, define both an inverse relationship
of
and a relation multiplication * between
and
as follows:
and
.
The relation
is called a reasonable relation if
.
A generalized reasoning of a general set
is defined as for any a non empty relation set
there is a relation
such that
.
Lemma 2.1. For any a relation set
, the following statements are true.
(1) The associative law is formed naturally, i.e.,
(2) Inverse operation is similar to that of matrix, i.e.,
(3) Maintain collections subordinate relations of the relation multiplication *, i.e.,
if
(4) Maintain collections subordinate relations of the inverse relationship
, i.e.,
if
Proof. (1). For any one
, by the definition of the relation multiplication *, there is a
such that
,
.
Thus, there is a
such that
.
Hence, there is a
such that
.
Therefore,
. It means that
.
Similarly to prove:
If
, then must be
. Otherwise, if
, then there is
such that
. This is a contradiction. Thus, the following result can be obtained
.
(2) For any one
, by the definition of the inverse relationship
, there is
.
By the definition of the relation multiplication *, there is a
such that
.
Thus, by the definition of the inverse relationship
again, there are
Hence, by the definition of the relation multiplication *, the following result can be obtained
.
Therefore,
.
Similarly, for any one
, by the definition of the relation multiplication *, there is a
such that
.
Thus, by the definition of the inverse relationship
again, there are
.
Hence, by the definition of the relation multiplication *, the following result can be obtained
.
Then, by the definition of the inverse relationship
again, the following result can be gotten
.
Therefore,
.
Comprehensive above, the desired conclusion can be achieved:
.
(3) Assume that
.
For any one
, by the definition of the relation multiplication *, there is a
such that
.
Thus, by the definition of collections subordinate relations
,
, there are
Thereby, by the definition of the relation multiplication * again, there is
.
Therefore, there is
.
Similarly, it is proved that
(4) Assume that
.
For any one
, by the definition of the inverse relationship
, there is a relation
.
Thus, by the definition of collections subordinate relations
,
, there is
, Thereby, by the definition of the inverse relationship
again, there is
. Therefore, there is
,
.
Similarly, it is proved that
It completes the proof. #
Corollary 2.1. For any a relation set
, assume that
.
Then the following statements are true.
(1)
.
(2)
.
(3)
Proof. (1) Assume that
By (4) of Lamma 2.1, there is
By (2) of Lamma 2.1, there is
(2) Assume that
By (3) of Lamma 2.1, there are
(3) Assume that
By the result in (1), there is
Because each of the relations
is reasonable, so
.
Thus, by (3) of Lamma 2.1, there are
By (2) of Lamma 2.1, there are
It completes the proof. #
By Lemma 2.1, the generalized relationship reasoning satisfies the associative law of reasoning, i.e.,
The associative law is the basic requirement of reasoning in TCP or TCMath. But there are a lot of reasoning forms which do not satisfy the associative law of reasoning in Western Mathematics.
For example, in the true and false binary of proposition logic, the associative law of reasoning does not hold since
2.2. Equivalence Relations of Non-Authigenic Logic
Let
be a non empty set (the collection
of the research objects) and
be its a relation. It is called an equivalence relation, denoted by ~, if the following 3 conditions are all true:
(1) Reflexive:
for all
; i.e.,
;
(2) Symmetric: if
, then
; i.e., if
, then
;
(3) Conveyable (Transitivity): if
, then
; i.e., if
and
, then
.
A relation
is called a compatibility relation if there is a non empty subset
such that the non empty subset
satisfies at least one of the conditions above.
A relation
is called an incompatibility relation if there is not any a non empty subset
such that the non empty subset
satisfies at least one of the conditions above.
Any one of compatibility relations can be expanded into an equivalence relation to some extent. That is to say, in a certain logic analysis macro or global level, any a compatible relation
can be handled as an equivalence relation
.
Western Mathematics only considers the reasoning under one Axiom system such that only compatibility relation reasoning is researched. However there are many Axiom systems in nature. TCP or TCMath mainly researches the relation reasoning among many Axiom systems in nature. Of course, she also considers the relation reasoning under one Axiom system but she only expands the reasoning as the equivalence relation reasoning.
2.3. Two Kinds of Opposite Incompatibility Relations of Non-Authigenic Logic
Equivalence relations, even compatibility relations, can not portray the structure of the mathematical complex systems clearly. In the following, two incompatibility relations can be considered.
In TCP or TCMath, the non-authigenic logic having another name: image mathematics in Zhang & Shao (2012), any an Axiom system is not considered, but should first consider to use a logic system. Believe that the rule of Heaven and the behavior of Human can follow the same logic system (天人合一) in Zhang (2018b). This logic system is equivalent to a group of computation. The method is to abide by the selected logic system to the research objects classification, without considering the specific content of the research object, namely, classification taking images (比类取象). Analysis of the relationship between research objects, make relationships with a computational reasoning comply with the selected logic system operation. And then consider the research objects of the specific content of the conditions, according to the logic of the selected system operation to solve specific problems. In mathematics, the method of classification taking images is explained in the following Definition 2.1.
Definition 2.1. Suppose that there exists a finite group
of order m where
is identity. Let
be a none empty set which can be classified into some classes satisfying that
where the notation means that
,
,
(the following the same).
In image mathematics, the
is first called a factor corresponding to the group element
for any j, and
is called a factor space (all “Hexagram” (卦)). People do not consider the factor size (as class variables) and only consider it as mathematical symbols (“Hexagram” (卦)), such as, −1 or 1, because the size is defined by a human behavior for
, but people have no assumption of
.
A mathematical index of the unknown multivariate function
, is called a function image of
. All mathematical indexes of the unknown multivariate function f compose of the formation of a new set, namely, the image space
where
is also a finite group of order q where
is identity. The
is also called an Axiom system for any j if at least
because any an Axiom system is the assumption of
in which there are only the compatibility relations, i.e., pursuing the same mathematics index
.
The special multivariate function f (i.e., special function image) is not considered and only the calculation way of the general mathematical indexes of f is considered from the factor space
in order to know some causal relations, because of no assumption of f. But the size of the data image should be considered if specific issues are studied by the general rule of data images.
In other words, on one hand, a study of the hexagrams (“Hexagram” (卦)) in image mathematics is to learn the generalized properties of the inputs
of any a multivariate function f for the given factor space
, such as all inputs
are the non-size and non-order relations, but there are orthogonal relations among some inputs
, there are also symmetrical relations among some inputs
, and only there is an equivalence relation among all inputs
for any j, and so on.
On the other hand, a study of the image (“Xiang” (象)) in image mathematics is to learn the generalized properties of all outputs inputs
for the image space
, such as all outputs
are size specific meaning and a sequence of relationship, but there are the killing relations among some outputs
, and there are also the loving relations among some outputs
, and only there is a liking relation among all outputs
for any j, and so on.
Without loss of generality, the function image space
and the factor space
are putted, still keep for
because of no assumption of
and
. In order to study the generalized relations and generalized reasoning, image mathematics researches the following relations.
Assume that
,
where the note
is the usual Decartesian product or cross join. Define relations
Here the note
is called an equivalence relation of
if
is identity; denoted by ~;
The note
is called a symmetrical relation of
if
; denoted by
or
;
The note
is called a neighboring relation of
if
; denoted by
or
;
The note
is called an alternate (or atavism) relation of V if
; denoted by
or
.#
In this case, the equivalence relations and symmetrical relations are compatibility relations but both neighboring relations and alternate relations are incompatibility relations. These relations are all reasoning relations since the relation
if
.
The equivalence relation
, symmetrical relations
’s, neighboring relation
and alternate relations
’s are all the possible relations for the method of classification taking images. In the following, the equivalence relation
, the neighboring relation
and the alternate relations
are mainly considered.
Assume there is an energy function on
(see Zhang & Shao (2012)). In the future, the equivalence relation
will be the liking relation, the symmetrical relations
’s will be the reciprocal causation relations, the neighboring relation
will be the loving relation and the alternate relations
’s will be the killing relations. In the following, the liking relation
, the loving relation
and the killing relations
are mainly considered.
For example, there is a unique generalized logic reasoning model between the two kinds of opposite incompatibility relations for case
. Let
be a none empty set, there are two kinds of opposite relations: the neighboring relation
, denoted
and the alternate (or atavism) relation
, denoted
, having the following property:
(1) If
, then
, i.e., if
, then
, or,
;
If
, then
, i.e., if
, then
, or,
;
If
, then
, i.e., if
, then
, or,
.
(2) If
, then
, i.e., if
, then
, or,
;
If
, then
, i.e., if
, then
, or,
;
If
, then
, i.e., if
, then
, or,
.
Let
and
. Then above reasoning is equivalent to the calculating as follows:
where the
is the addition of module 5.
Two kinds of opposite relations can not exist separately. Such reasoning can be expressed in Figure 1 and Figure 2. The first triangle reasoning is known as a jumping-transition reasoning in Figure 1, while the second triangle reasoning is known as an atavism reasoning in Figure 2.
Reasoning method is a triangle on both sides decided to any a third side. Both neighboring relations and alternate relations are not compatibility relations, of course, not equivalence relations, called incompatibility or compatibility relations.
2.4. Genetic Reasoning of Non-Authigenic Logic
Let
be a none empty set (the collection
of the research objects) with the equivalent relation
, the neighboring relation
and the alternate relations
. Then a genetic reasoning is defined as follows:
(1) If
, then
,i.e., if
, then
, or,
;
(2) If
, then
, i.e., if
, then
, or,
;
(3) If
, then
, i.e., if
, then
, or,
;
(4) If
, then
, i.e., if
, then
, or,
.
The genetic reasoning is equivalent to that there is a group
with the operation
such that
can be classified into
where
may be an empty set and
,
, satisfying
,
.
2.5. Steady Multilateral Systems of Non-Authigenic Logic
For a none empty set
(the collection
of the research objects) and its some relations
,
, the form
(or simply,
) is called a multilateral system, if
satisfies the following properties:
(a) (uniqueness)
.
(b) (hereditary, or identity, or macro)
.
(c) (invertibility) For any
, there is
.
(d) (generalized reasoning) For any
, there exists
such that
.
The (d) is called the generalized reasoning, the (a) the uniqueness of the generalized reasoning, the (b) the hereditary (pass on from generation to generation) of the generalized reasoning (or genetic reasoning) and the (c) the equivalent property of the generalized reasoning of both relations
and
, i.e., the reasoning of
is equivalent to the reasoning of
. In this case, the two-relation set
is a lateral relation of
.
Furthermore, the
and
are called the state space and relationship set of
considered, respectively. The mathematical complex system
can be written as
where
is called the equivalent relation or identity or macro-variable of
.
For a multilateral system
, it is called complete (or, perfect) if “
” changes into “=”. And it is called complex if there exists at least a incompatibility relation
. In this case, the multilateral system is also called a logic analysis model of a mathematical complex system in Zhang & Shao (2012).
Let
be a incompatibility relation. The multilateral system
is said as a steady multilateral system (or, a stable multilateral system) if there exists a number n such that
where
.
The condition is equivalent to there is a the chain
such that
, i.e.,
.
The steady multilateral system is equivalent to the complete multilateral system. The stability definition given above, for a relatively stable system, is most essential. If there is not the chain or cycle, then there will be some elements without causes or some elements without results in a system. Thus, this system is to be in the persistent state of finding its results or causes, i.e., this system will fall into an unstable state, and there is not any stability to say.
Lemma 2.2. The mathematical complex system
is a multilateral system if and only if there exists a group
of order m where
is identity such that the relation set
satisfies
,
. The state space can be classified into
where
may be an empty set such that
,
.
Proof. Let a multilateral system
.
Because only the relation of the group of order m is considered, so can the serial number of the relationship with a group of Numbers to remember.
Let the group of order m is
where
is identity. Then consider the all relations
,
.
So, the classification of the space at least there should be a group of number. In other words, n is greater then or equal to m. In the following, it is proved that n is not greater than m. It is proved by using the reduction to absurdity.
If
, there is a space
such that
Thus
.
Because by the definition of the relations, there is
,
so the condition (a) of the multilateral system is not true, i.e.,
. It is because
. This is a contradiction since
. Thus
.
But there is also the case
. For example, let
Taking
, can consider
. Directly calculating the relations of the steady multilateral system with three elements, it is to get
It satisfies the condition (a) of the multilateral system:
.
Therefore, if
, people can add some empty set to make the multilateral system for the state space satisfying
On the other hand, the definition of directly using the relationship between operations shows the following conclusions:
It is because for the multiplication of relations, the calculation of the relation
is only to consider the relation between
and
whether there is a common element. But there is a set relation
and
,
,
. Thereby, whether there is a common element between
and
is
equivalent to that whether there is a common element between
and
, i.e., whether
is an empty set. Thus
.
Therefore, the mathematical complex system
is a multilateral system if and only if there exists a group
of order m where
is identity such that the relation set
satisfies
,
.
The state space
can be classified into
where
may be an empty set. It completes the proof. #
In this case, the multilateral system
can be written as
satisfying
Here
may be an empty set. There is an Axiom system
if at least
. #
Lemma 2.3. If the following multilateral system is a steady multilateral system:
Then
and
is a group of order m about multiplication
where
must be at least a non empty set for any i. #
Proof. By Lemma 2.2, there is
If the following multilateral system is a steady multilateral system:
then
(a) (uniqueness)
.
(b) (hereditary, or identity, or macro)
,
.
(c) (invertibility) For any
, there is
,
.
(d) (generalized reasoning) For any
, there exists
such that
By the definition of group, the
is a group of order m about multiplication
Here,
is identity of the group
and
is the inverse of
of the group
for any a
.
In the following, it just need to be proved that if the multilateral system
is a steady multilateral system, then
must be at least a non empty set for any a
.
It is because, if
is a non empty set for all
, then
. It is proved by using the reduction to absurdity.
In fact, if only
for some
, there are
such that
,
, thus
,
. Thereby
.
The definition of directly using the multiplication relationship between relation operations shows the following conclusions:
It is because for the multiplication of relations, the calculation of the relation
is only to consider the relation between
and
whether there is a common element. But there is a set relation
and
,
,
. Thereby, whether there is a common element between
and
is equivalent to that whether there is a common element between
and
, i.e., whether
is an empty set. Thus
.
Continue to calculate the relationship of
, there is
This is a contradiction to the definition of the steady multilateral system. It is because the definition of the steady multilateral system should be
,
. It completes the proof. #
Definition 2.2. Let the multilateral system
can be written as
satisfying
,
,
,
. The group
of order m, where
is identity, is called the representation group of the multilateral system
.
Denoted the generalized difference in, set
based on the group
, called the representing function of relation
. The representing function has nothing to do with the collection
of the research objects.
Let multilateral systems
be with two representation groups
, respectively. Both multilateral systems
are called isomorphic if the two representation groups
are isomorphic. #
Lemmas 2.2 and 2.3 and Definitions 2.1 and 2.2 are the key to concepts in multilateral system theory because they show the classification taking images as the basic method. In the following, introduce two basic models to illustrate the method.
Lemma 2.4. Suppose that
with multiplication table
i.e., the multiplication of
is the addition of module 2. In other words,
.
And assume that
, where
,
satisfying
.
Then
is a steady multilateral system with one equivalent relation
and one symmetrical relation
.
The system is simple since there is not any incompatibility relation. In other words, the relations
’s are the simple forms as follows:
where
is corresponding to
.
In the sense of isomorphism, there is only one unique steady multilateral system
. #
Proof. Because in the sense of isomorphism, dual group only Lemma 2.4 defined in a structure, so Definition 2.2, up to isomorphism only Lemma 2.4 defined in this a multilateral system.
In fact, for the steady multilateral system
, if
,
, then
,
. Thus in the sense of isomorphism,
is isomorphic to the group
.
The relation
is an equivalent relation and
is a symmetrical relation since
. Of course, they are the compatibility relations.
Because in the sense of isomorphism, there is only one unique group
, so in the sense of isomorphism, there is only one unique steady multilateral system
. It completes the proof. #
The steady multilateral system in Lemma 2.4 is the reasoning model of “Tao” (道) or “Yin-Yang” (阴阳) in TCP or TCMath if there are two energy functions
and
satisfying
, called Tao model, denoted by
where
is called Yin (阴) state of
and
is called Yang (阳) state of
.
Lemma 2.5. Suppose that
with multiplication table
i.e., the multiplication of
is the addition of module 5. In other words,
. And assume that
,
,
where
satisfying
.
Then
is a steady multilateral system with one equivalent relation
and one loving relation
and one killing relation
. The relations
and
are two incompatibility relationships.
The system is complex since there are two incompatibility relationships. In other words, the relations
’s are the simple forms as follows:
where
is corresponding to
.
In the sense of isomorphism, there is only one unique steady multilateral system
. #
Proof. Because in the sense of isomorphism, dual group only Lemma 2.5 defined in a structure, so Definition 2.2, up to isomorphism only Lemma 2.5 defined in this a multilateral system.
In fact, for the steady multilateral system
, if
then
.
The relation
is an equivalent relation. Of course, it is a compatibility relationship. And
is an incompatibility relation as the loving relationship since
,
;
;
and
,
.
And
is an incompatibility relation which can be as the killing relationship of the multilateral system
since
,
;
;
and
,
,
,
.
Thus in the sense of isomorphism,
is isomorphic to the group
.
Because in the sense of isomorphism, there is only one unique group
, so in the sense of isomorphism, there is only one unique steady multilateral system
. It completes the proof. #
2.6. Yin Yang Wu Xing Model of Non-Authigenic Logic
In order to apply the reasoning to other fields rather than the health of a mathematical multilateral complex system, Zhang & Shao (2012) have started a steady multilateral system imitating a mathematical multilateral complex system. A most basic steady multilateral system is as follows.
Theorem 2.1. Feng et al. (2005) For each element x in a steady multilateral system
with two incompatibility relations, there exist five equivalence classes below:
which the five equivalence classes have relations in Figure 3. #
The Yin Yang Wu Xing model can be written as follows: Define
![]()
Figure 3. Finding Yin Yang Wu Xing Model.
corresponding to wood, fire, earth, metal, water, respectively, and assume that
where
.
And assume that
satisfying
where
is the Descartesian product in set theory and the following note
is the relation multiplication operation. The relation multiplication of
is isomorphic to the addition of module 5.
Then
is a steady multilateral system with one equivalent relation
and two incompatibility relations
and
where the note
is the relation inverse operation.
For the reasoning model of Yin Yang Wu Xing in TCP or TCMath, the words “Yin Yang” means there are two incompatibility relations
and
, where the neighboring relation
is the loving relation, also called Yang relation or interpromoting relation (相生) among five subsets
’s, and the alternate relation
is the killing relation, also called Yin relation or restriction relation (相克) among five subsets
’s; The words “Wu Xing” means there are five subsets
’s such that
where there is only the equivalence relation
among interior for each of five subsets
’s, and there are Yin or Yang relations among exterior for all five subsets
’s. The five subsets
’s do not means the five elements (metal, wood, water, fire and earth), but with philosophical meaning of five aspects corresponding to the five subsets
’s.
It can be proved that the steady multilateral system in Theorem 2.1 is the reasoning model of Yin Yang Wu Xing in TCP or TCMath if there is an energy function
satisfying
The parameter
is called the coefficient of the vital or righteousness energy. The parameter
is called the coefficient of the evil energy. A mathematical complex system is called healthy if the vital or righteousness coefficient
is greater than or equal to the evil coefficient
. Otherwise, the mathematical complex system is called unhealthy. For a healthy mathematical complex system, the transfer law of the Yang vital or righteousness energy in the Yin Yang Wu Xing Model is
Figure 3 in Theorem 2.1 is the figure of Yin Yang Wu Xing theory in Ancient China. The steady multilateral system
with two incompatibility relations is equivalent to the logic architecture of reasoning model of Yin Yang Wu Xing theory in Ancient China. What describes the general method of the steady multilateral system
with two incompatibility relations can be used in any a mathematical complex system.
Non-authigenic logic of TCP or TCMath is similar to a group which has nothing to do with the research objects in Zhang & Shao (2012). In order to ensure the reproducibility such that the analysis conclusion can be applicable to any a mathematical complex system, a logic analysis model can be chosen which has nothing to do with the object of study. TheTao model of Yin and Yang is a generalized one which means that two is basic. But theTao model of Yin Yang is simple in which there is not incompatibility relation. The analysis conclusion ofTao model of Yin Yang cannot be applied to an incompatibility relation model. Thus the Yin Yang Wu Xing model with two incompatibility relations of Theorem 2.1 will be selected as the logic analysis model in this paper.
Study of a mathematical complex system is the key to pathological diagnosis and treatment of a mathematical complex system, also known as interference. Any steady multilateral system with an energy function, an intervention response capacity and a self-protection capacity, is a logic to study the specific object of non-authigenic logic. According to non-authigenic logic thought, the stand or fall of the intervention method for a steady multilateral system imitating a mathematical complex system, depends on a mathematical complex system’s both side effects issue and mathematical intervention resistance problem from the intervention. Whether it can promote the health of the mathematical complex system without side effects issue? Whether it can promote the response ability to the intervention of the mathematical complex systems and self-protection ability without mathematical intervention resistance problem? These standards have nothing to do with mathematical researches. The intervention methods of this mathematical complex system are in Zhang (2011a, 2011b, 2020), Zhang & Zhang (2019) and Zhang et al. (2021a, 2021b) in general, are as follows:
(1) “Virtual disease with a healthy mathematical complex system is to fill its mother but real disease with a healthy mathematical complex system rushes down its son” (虚则补其母,实则泄其子) if only one subsystem of the mathematical complex system falls ill or if only two subsystems with the loving relation of a mathematical complex system encounter usual sick for a healthy mathematical complex system in Zhang (2011a, 2011b).
(2) “Virtual disease with an unhealthy mathematical complex system is to fill itself but real disease with an unhealthy mathematical complex system rushes down itself” (虚则补之,实则泄之) if only one subsystem of the mathematical complex system falls ill or if only two subsystems with the killing relation of a mathematical complex system encounter usual sick for an unhealthy mathematical complex system in Zhang (2011b) or Zhang & Zhang (2019).
(3) “Strong inhibition of the same time, support the weak” (抑强补弱,或者,泄南补北) if only two subsystems with a killing relation of a mathematical complex system encounter usual sick, which destroyed the killing relation of the mathematical complex system in Zhang (2011a), or Zhang (2020).
(4) “Do not treat a disease after it has occurred. But treat the disease before it will occur” (不治已病治未病) if there are a lot of subsystems of a mathematical complex system encountering sick for a long time in Zhang (2011b) or Zhang (2020).
(5) “Searching for the primary cause of disease in treatment and cure both symptoms and root-cause at the same time” (治病求本,标本兼治) if there are a lot of subsystems of a mathematical complex system encountering sick for a long time in Zhang & Zhang (2019).
(6) “Even if all changed, it is hard to change one’s nature” (江山易改,本性难移) if there are a lot of subsystems of a mathematical complex system encountering sick for a long time in Zhang et al. (2021a).
(7) “Seize the momentum of development, hasten lucky avoids disaster” (顺势而为,趋吉避凶) if there are a lot of subsystems of a mathematical complex system encountering sick for a long time in Zhang et al. (2021b).
The combination of Yin Yang Wu Xing theory with the problem in question of TCP is not quite well-founded. The key is the philosophical meaning of five aspects of non-authigenic logic. The steady multilateral complex system is used to simulate the complex system of human body. The philosophical meaning of five aspects of non-authigenic logic can be used to TCP itself. The following conclusions are drawn.
All healing methods represent cognition, equivalent to wood. These treatments include the following.
For example, “Virtual disease with a healthy mathematical complex system is to fill its mother but real disease with a healthy mathematical complex system rushes down its son” (虚则补其母,实则泄其子)
“Virtual disease with an unhealthy mathematical complex system is to fill itself but real disease with an unhealthy mathematical complex system rushes down itself” (虚则补之,实则泄之).
“Strong inhibition of the same time, support the weak” (抑强补弱,或者,泄南补北), and so on.
Similarly, all logic problems represent cognition, equivalent to wood. The non-authigenic thinking or no Axiom system (无公理系统) is the key to the non-authigenic logic, liking wood.
All disease transmission methods represent development, equivalent to fire. These disease transmission methods include the following.
There are healthy people and unhealthy people about the development of disease. The methods of disease transmission vary from body to body. Treatment should be tailored to different people. Do not treat the disease that has already occurred, and treat the disease that has not occurred but will occur by following the disease transmission method.
For example, “Do not treat a disease after it has occurred. But treat the disease before it will occur” (不治已病治未病), and so on.
Similarly, all loving or interpromoting relation problems represent developing, equivalent to fire. The loving or interpromoting analysis (相生分析) is the preconception principle of the non-authigenic logic, liking fire.
All zangxiang and jingluo methods represent combining, equivalent to earth. These zangxiang and jingluo methods include the following.
For example, “Searching for the primary cause of disease in treatment and cure both symptoms and root-cause at the same time” (治病求本,标本兼治), and so on.
Similarly, all killing or restriction or checking relation problems represent combining, equivalent to fire. The killing or restriction or checking analysis (相克分析) is the integration coordination combination principle of the non-authigenic logic, liking earth.
All eight palaces or eight veins methods represent accepted, equivalent to metal. These eight palaces or eight veins methods include the following.
For example, “Even if all changed, it is hard to change one’s nature” (江山易改,本性难移), and so on.
Similarly, all killing or restriction or checking reproducibility problems represent accepted, equivalent to metal. The killing or restriction or checking reproducibility (相克再现性) is the logic layering principle of the non-authigenic logic, liking metal.
All sixty JiaZi methods represent risk, equivalent to water. These sixty JiaZi methods include the following.
For example, “Seize the momentum of development,hasten lucky avoids disaster” (顺势而为,趋吉避凶), and so on.
Similarly, all loving or interpromoting reproducibility problems represent risk, equivalent to metal. The lovling or interpromoting reproducibility (相生再现性) is the automation principle of the non-authigenic logic, liking water.
The steady multilateral complex system is used to simulate the complex system of TCP. The combination of Yin Yang Wu Xing theory with the problem in question of TCP is obtained by the philosophical meaning of five aspects of non-authigenic logic. A lot of ideas can be obtained similar to the philosophical meaning of five aspects of non-authigenic logic.
2.7. Some Examples of the Steady Multilateral Systems of Non-Authigenic Logic
For the steady multilateral systems, there are a lot of models which satisfy the generalized relations and the generalized reasoning. The following are some examples.
(1) Suppose that
where
is identity. Its multiplication table is as follows:
The steady multilateral system
is called the three types of talent model, denoted simply by
, if it satisfies the following conditions:
The system is complex since there is only one incompatibility relationship. In other words, the relations
’s are the simple forms as follows:
The relation
is the equivalent relation. Of course, it is a compatibility relation. Only there is one incompatibility relationship
since
and
,
;
;
.
The incompatibility relation
is a loving relationship of the steady multilateral system
since
.
Here, the number 1 or 2 or 3 is called the tengen (天元), the earth material (地元), the people ability (人元), corresponding to heaven (1), earth (2) and people (3), respectively. The set of {1, 2, 3} is called the three types of talent or material set.
In TCMath, any material can be found, not Yang is Yin. No matter of Yin and Yang are unable to see, known as dark matter, or nonphysical. Therefore, the Tao force is often exist in the physical world. Any steady multilateral system only force under the action of the Tao, may be to be perceived.
In TCMath, there is a generalized Yin Yang Wu Xing complex system model: Nature, Tao, Heaven, Earth, People. {Nature, Tao} is called as Yang. And {Heaven, Earth, People}, namely, three types of talent or material, is called as Yin.
It is believed that any a Yin Yang Wu Xing complex system is made up of three types of talent or material to combined changes. The three types come from the Yin energy in it’s a layer Yin Yang Wu Xing system. It is because a lot of complex systems can be seen as a Yin Yang Wu Xing system. However, any Yin Yang Wu Xing system is a mathematical complex system observation of the objective fact in one logic level, it will be a layer of the Yin Yang Wu Xing system of restriction and generation. In the Yin Yang Wu Xing system, both wood and fire are Yang; three types including earth, metal and water are Yin. So any Yin Yang Wu Xing system is generated by the three talents (earth, gold and water) at the upper logical level. The three types are generated from an upper layer of the Yin Yang Wu Xing system. For example, an upper layer of controlling on the Yin Yang Wu Xing system of mathematical complex system is the nature, Tao, heaven, earth and people system, so the formation of the mathematical complex system three materials are heaven (1), earth (2) and people (3).
(2) Suppose that the following set
is a group of order 6, where
is identity. Its multiplication table is as follows:
The steady multilateral system
is called the Telluric effluvium model, denoted simply by
, if it satisfies the following conditions:
The number 1 or 2 or 3 is called the tengen (天元), the earth material (地元), the people ability (人元), corresponding to heaven (1), earth (2) and people (3), respectively. The set of {1, 2, 3} is called three types of talent or material group. The three types heaven (1), earth (2) and people (3) to any change combine forming the elements of Telluric effluvium model as follows:
It is with elements,
. The each of elements,
, is called the primordial energy (元气), essence derived from food (谷气), defensive energy (卫气), essential substance circulating in the Meridians and blood Meridians (营气), genuine energy (真气), pectoral energy (宗气), respectively.
Another name of the elements,
, is respectively
Generally positive or Yang material, they are able to be perceived, but few can see the material itself, can only use signs. Therefore, the Yang energy symptoms of the set
is call the marrow energy (髓); The Yin energy of the set
is call the blood energy (血); The Yin energy of the set
is call the saliva energy (津); The Yin energy of the set
is call the essence of water and grain (水谷精微).
Growth and conveyance in the six energies
known as the six roots (根); As the fruit of these six energies
known as the six fruits (结); Storage of these four energies
known as the four seas (四海); Energy exchange of the four kinds of
known as the four streets (四街). Of course, for a healthy mathematical complex system, the transfer law of each of the six energies
is from its root (root-causes) (根) to its fruit (symptoms) (结).
(3) Suppose that the following set
is a group of order 8, where
is identity. Its multiplication table is as follows:

The three Tao model can combine forming a steady multilateral system
is called the Eight-Hexagram (八卦) model, denoted simply by
which satisfies the following conditions:
The number
is called the Qian (乾), Dui (兑), Li (离), Zhen (震), Xun (巽), Kan (坎), Gen (艮), Kun (坤) respectively. The set of
is called the Eight-Hexagram (八卦) system.
(4) Zhang & Zhang (2019) Suppose that the following set
is a group of order 8, where
is identity. Its multiplication table is as follows:

Assume the Yin Yang Wu Xing model
is implemented by the Tao force of the Tao model
. Then the steady multilateral system
is called the Zangxiang or Five Zang-organs model of the steady multilateral system.
The Zangxiang model satisfies as follows:
Each of the elements,
is called respectively
corresponding to the Chinese words respectively:
also corresponding to the notations in Theorem 3.1 respectively:
Here,each of the elements:
is called wood,fire, earth, metal, water,respectively,and this is
Yang,
is Yin.
In TCMath, another name of the Zangxiang system is the ten Heavenly Stems (天干). It means in the changes of energy transmission, plays a major role, is under the power of positive (Yang), although it is invisible, the reason of behind the sign.
(5) Zhang & Zhang (2019) Suppose that the following set
is a group of order 12, where
is identity. Its multiplication table is as follows:
Assume the Telluric effluvium model
is implemented by the Tao force of the Tao model
. Then the steady multilateral system
is called the Jingluo or the Six Fu-organs model of the steady multilateral system.
The Jingluo model satisfies as follows:
Each of the elements,
is called respectively
Corresponding to the Chinese words respectively:
Also corresponding to the notations in Theorem 3.1 as the five viscera and six entrails respectively:
Here, each of the elements:
is called wood, xiang-fire (相火), earth, metal, water, jun-fire (君火) respectively, and this is
Yang,
is Yin.
In TCM, an other name of the Jingluo system is the twelve Earthly Branches (地支). It means in the changes of energy transmission, plays a secondly role, is under the power of negative (Yin), although it is tangible, a sign of strength can be observed directly.
(6) Zhang et al. (2021a) Suppose that the following set
is a group of order 64, where
is identity. Its multiplication table is with that of the Descartesian product
of the group
in set theory.
Assume that the Eight-Hexagram model
is implemented by the Eight- Hexagram force of the Eight-Hexagram model
. Then the steady multilateral system
is called the model of eight palaces or eight veins of the steady multilateral system.
The model satisfies as follows:
Here, the multiplication operation * is that of the Eight-Hexagram Model.
Each of the elements,
is called respectively
corresponding to the Chinese words respectively:
乾(1, 1), 姤(1, 5), 遁(1, 7), 否(1, 8), 观(5, 8), 剥(7, 8), 晋(3, 8), 有(3, 1);
兑(2, 2), 困(2, 6), 萃(2, 8), 咸(2, 7), 蹇(6, 7), 谦(8, 7), 小(4, 7), 妹(4, 2);
离(3, 3), 旅(3, 7), 鼎(3, 5), 未(3, 6), 蒙(7, 6), 涣(5, 6), 讼(1, 6), 人(1, 3);
震(4, 4), 豫(4, 8), 解(4, 6), 恒(4, 5), 升(8, 5), 井(6, 5), 大(2, 5), 随(2, 4);
巽(5, 5), 畜(5, 1), 家(5, 3), 益(5, 4), 妄(1, 4), 嗑(3, 4), 颐(7, 4), 蛊(7, 5);
坎(6, 6), 节(6, 2), 屯(6, 4), 既(6, 3), 革(2, 3), 丰(4, 3), 明(8, 3), 师(8, 6);
艮(7, 7), 贲(7, 3), 畜(7, 1), 损(7, 2), 睽(3, 2), 履(1, 2), 孚(5, 2), 渐(5, 7);
坤(8, 8), 复(8, 4), 临(8, 2), 泰(8, 1), 壮(4, 1), 夬(2, 1), 需(6, 1), 比(6, 8).
Also corresponding to the notations in Theorem 3.1 respectively:
Here, each of the elements:
is called wood, fire, earth, metal, water, respectively, and this is
Yang,
is Yin.
Each of sets:
is called Qian palace (乾宫), Dui palace (兑宫), Li palace (离宫), Zhen palace (震宫), Xun palace (巽宫), Kan palace (坎宫), Gen palace (艮宫), Kun palace (坤宫), respectively.
(7) Zhang et al. (2021b) suppose that the ten heavenly stems model and the twelve earthly branches model are respectively
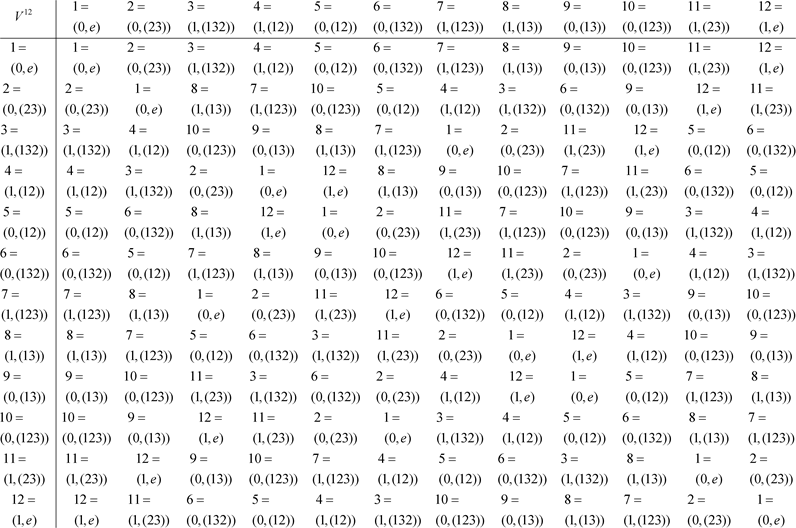
Then the following model in Table 1 is called the sixty JiaZi model.
In Table 1, each of the elements (1, 0), (0, 0), ..., (0, 4) is that of group
as the ten heavenly stems model or Zangxiang Model
In Table 1, each of the elements (0, e), (0, (23)), ..., (1, e) is that of group
as the twelve earthly branches model or Jingluo Model.
In Table 1, each of the elements of the set
![]()
Table 1. Sixty JiaZi for name, ten heavenly stems, twelve earthly branches and Yin Yang attribute.
is called the number of Sixty JiaZi. Another way to write the number sixty JiaZi is as follows:
1 = (1, 1, 1) 2 = (0, 2, 2) 3 = (1, 3, 3) 4 = (0, 4, 4)
5 = (1, 5, 5) 6 = (0, 6, 6) 7 = (1, 7, 7) 8 = (0, 8, 8)
9 = (1, 9, 9) 10 = (0, 10, 10) 11 = (1, 1, 11) 12 = (0, 2, 12)
13 = (1, 3, 1) 14 = (0, 4, 2) 15 = (1, 5, 3) 16 = (0, 6, 4)
17 = (1, 7, 5) 18 = (0, 8, 6) 19 = (1, 9, 7) 20 = (0, 10, 8)
21 = (1, 1, 9) 22 = (0, 2, 10) 23 = (1, 3, 11) 24 = (0, 4, 12)
25 = (1, 5, 1) 26 = (0, 6, 2) 27 = (1, 7, 3) 28 = (0, 8, 4)
29 = (1, 9, 5) 30 = (0, 10, 6) 31 = (1, 1, 7) 32 = (0, 2, 8)
33 = (1, 3, 9) 34 = (0, 4, 10) 35 = (1, 5, 11) 36 = (0, 6, 12)
37 = (1, 7, 1) 38 = (0, 8, 2) 39 = (1, 9, 3) 40 = (0, 10, 4)
45 = (1, 5, 9) 46 = (0, 6, 10) 47 = (1, 7, 11) 48 = (0, 8, 12)
49 = (1, 9, 1) 50 = (0, 10, 2) 51 = (1, 1, 3) 52 = (0.2, 4)
53 = (1, 3, 5) 54 = (0, 4, 6) 55 = (1, 5, 7) 56 = (0, 6, 8)
57 = (1, 7, 9) 58 = (0, 8, 10) 59 = (1, 9, 11) 60 = (0, 10, 12).
There exists a one-to-one correspondence between the above two sets. #
3. The Negative Philosophical Answer of Hilbert Sixth Mathematical Conjecture
3.1. Philosophical Meaning of Each of Five Aspects of Non-Authigenic Logic
The following cognitive logic of five aspects philosophical meaning is due to Taoism, called cognitive logic of non-authigenic or cognitive logic of automation or cognitive logic of “Wu Xing”, etc., it applies to any a steady multilateral system imitating a mathematical complex cognitive system. The basic idea is classified into five steps, called wood, fire, earth, metal, water. Every step has a principle and three rules. Principle provides basic idea. The rules provide specific practices. Specific practices include how to think, how to do, how to keep continuously developing.
In fact, it is also the logical system of TCP. The wood, fire, earth, metal, water are states of qi or Chi or energy of the system. The idea of obtaining image from classification or classification taking image technology comes from the states of qi or Chi or energy of the system. The logical system of TCP contains the following contents:
No suppose principle (无假设原则), don’t assume that teaching (不言施教), the criteria for comparison came from a third party (双方比较的标准来自于第三方), the non-authigenic thinking rule (不自生思维规则), the resource limited rule (资源有限规则), the fault-tolerant rule (容错规则), and so on, they’re always called the wood state of the Chi or the wood state of the energy of the system. That is equivalent to no single axiom postulates the system. Complex systems cannot be assumed.
The first impression is strongest (先入为主), preconception principle (先入为主原则), the objective consistency rule (客观一致性规则), and the repeatability rule (重复性规则), the default rule (默认规则), and so on, they’re always called the fire state of the Chi or the fire state of the energy of the system. That is equivalent to that there are multiple incompatible systems of axioms. Objective truth can only be recognized by using reproducibility.
The integration coordination combination principle (整体协调化合原则), the searching null composition rule (零成分搜索规则), integration capability (整合能力), the decomposition rule (分解规则), and so on, they’re always called the earth state of the Chi or the earth state of the energy of the system. That is equivalent to how to recognize the whole, adhere to the whole thinking. Zero component search is a necessary measure to identify the whole.
Logic layering principle (逻辑分层原则), Heaven and People as a whole (天人合一), the Global-Local thinking rule (从整体到局部思维), logic downward compatibility (逻辑向下兼容能力), the logic causal cycle rule (逻辑因果圈), or the logic causal chain (逻辑因果链), the seriousness of logic rule (逻辑的严肃性规则), and so on, they’re always called the metal state of the Chi or the metal state of the energy of the system. That is equivalent to how to obtain cognitive logic, adhere to the global to the local thinking. First the whole and then the part is the key technique of eastern thinking.
Automation principle (自动化原则), doing nothing, everything is done (无为而无不为), the intervention reaction rule (干预响应规则), the self-protection rule (自保护规则). the second physiologic system rule (第二生理系统规则), and so on, they’re always called the water state of the Chi or the water state of the energy of the system. That is equivalent to that the highest goal pursued by TCP’s logic is to do nothing without doing anything.
Among the five principles, the basic principles that play an important role as a necessary condition for the existence of the whole are the principle of no hypothesis and the principle of integration and coordination.
Among the five principles, the basic principles that play an important role as sufficient conditions for the existence or the normal running of the whole are the principle of no hypothesis, the principle of integration and coordination and the principle of automation.
Among the five principles, the basic principle that plays a leading role as a necessary and sufficient condition for the existence of the whole is a preconceived principle, which can be divided into two categories. One is Xiang-fire, which performs the normal functions of fire, and the other is Jun-fire, which performs the overall functions of the five elements of leadership.
(a) Wood (
): No assumption principle (无假设原则)
“No suppose principle” has another name: Don’t assume that teaching (不言施教). It means that without a priori axiom hypothesis conditions, only there is cognition, reasoning and analysis on the relationship of a steady multilateral system imitating a mathematical complex system. In the traditional Chinese saying is: not afraid not perceive afraid goods than goods (不怕不识货就怕货比货).
The ideology includes three aspects of content: one is how to think as non-authigenic thinking rule (不自生思维规则). All assumptions and inspection standards must come from the actual problem itself or the third party standard (第三方标准). In other words, the criteria for comparison came from a third party (双方比较的标准来自于第三方). The assumption or standard or criteria is not relevant to the analysis methods or the analysis scholars (忘我能力). Not accord to the observed data and the hypothesized research object itself. It is the core of non-authigenic thinking rule. Using put forward the assumption of non-authigenic thinking rule can guarantee the processing method is a general problem. According to the rule of non-authigenic thinking, any a non-authigenic hypothesis, the principle of no violation, is no assumption.
Even with the assumptions and inspection standards, so they are not able to be determined in the field of Mathematics, both the western Mathematics and the oriental Mathematics cannot define these assumptions and inspection standards in the areas themselves, they must be determined by unrelated third parties to mathematical fields.
Second is how to do as the resource limited rule (资源有限规则). It is recognized that resources are limited, not admit unlimited resources, all the way to solve the problem that must be solved within limited resources (有限能力). Within the scope of the limited resources to solve the problem, and guarantee that all things will be successful. According to the rule of limited resource, any a resource hypothesis, the principle of no violation, is no assumption.
Resource limited rule is due to that one doesn’t have to look at the collection
of the research objects, in which
can be classified into
, but to focus on how the cognition of the basic elements of a mathematical complex system exist happen? First of all, don’t think that the ability of mathematical researchers is infinite, infinite resources are not available. Any mathematical complex system just can be understood only to rely on very small limited resources to solve the problem. This is the basic point of non-authigenic logic.
Third is how to keep continuously developing as the fault-tolerant rule (容错规则). It is to allow the people to solve the problem within a certain range to make mistakes, including the assumption error (容错能力). Only permissible maximum human to make mistakes, what to do can continue. According to the rule of fault tolerance, any a fault tolerant hypothesis, the principle of no violation, is no assumption.
The mathematical researchers themselves, to solve the problem of a steady multilateral system imitating a mathematical complex system, also have many insufficient, cannot assume the ability of these people is very high, can make no mistake. It is understood only under the condition of assuming that these people often make mistakes, to try to solve the problem of a mathematical complex system. The basic conclusion of non-authigenic logic, therefore, cannot has too strong dependence with resources and hypothesis.
No assumption rule is the thinking way for the “wood” properties of a steady multilateral system imitating a mathematical complex system, and to consider the beginning problem of the mathematical complex system. It belongs to the Wood (
) subsystem of the mathematical complex system since it cognizes the structure of the mathematical complex system which is the beginning observation or birth stage of all things, just like in the Spring of a year. In the initial stages of a mathematical complex system, and in the absence of birth assumptions, the purpose of both the greatest possible to restrict the behavior of the mathematical researchers and achieving the preliminary cognition of the mathematical complex system is to make a mathematical complex system can be able to generate. In order to explain the occurrence state of all things, researchers must be in the absence of cognitive assumptions, with the above ways of thinking, to cognize the structure of the mathematical complex system first. The structure has nothing to do with the observer behavior, and only related to the birth state of the mathematical complex system. Only in this way, can understand the birth cause of a mathematical complex system, get real Wood (
) properties of a mathematical complex system, and get the most cognitive goals.
Under the principle of no assumption, the articles can refer to see Zhang (1993, 2007a, 2011a, 2011b, 2012), Zhang & Shao (2012) and Zhang & Zhang (2013). #
(b) Fire (
): preconception Principle (先入为主原则
The principle of that “The first impression is strongest” is also namely preconception. The word preconception, spelling for “Xian Ru Wei Zhu” (先入为主) in TCP or TCMath, useful refers to listen or to get the first impression often dominant in researchers mind, later to meet different opinions, is not easy to accept.
This principle contains three aspects: one is how to think as the objective consistency rule (客观一致性规则). The objective consistency (客观一致性), i.e., what researchers observed the conclusions and the objective facts are consistent? Respect for the objective facts is the core of the human mind. Only to respect the objective facts as an idea, can assure to observe it is correct. According to the objective rule of consistency, any an objective method to deal with problems, the principle of no violation, is preconception.
The preconception principle is also due to that the researcher doesn’t have to look at the collection
of the research objects, in which
can be classified into
, but to focus on how to accelerate the development of a mathematical complex system to eliminate interference? First of all, don’t think that the researchers observed the conclusions and the objective facts are consistent if researchers do not know the objective facts. But under the condition of objective conclusion assume that researchers know that, researchers can simulate test with researchers observation analysis method to the conclusions and the objective facts are consistent? In many simulation test under the condition of reasonable, can think of researchers’ observation analysis method is reasonable, with the objective consistency. Simulation is not proof, but at least it means that researchers used in the method has certain rationality. In TCP or TCMath, the simulation method is considered to be the key method of a mathematical analysis for determining the reproducibility. This is the basic point of non-authigenic logic.
Second is how to do as the repeatability rule (重复性规则). That is, what the relationship between the observed conclusions, which are obtained by different observers and different reasonable ways, are consistent? Observations of the fact that is objective, regardless of the observer, no matter what observation method, after fully observed, the conclusion there will be no big changes. This is because the objective conclusion is only one. Adhere to the repetitive rule, can guarantee that can do things correctly, because people’s doing things is difficult to know the objective conclusion. According to the rule of repeatability, any repeatability method to deal with problems, the principle of no violation, is preconception.
The repeatability means under the condition of the same work, measured in the same input values in the same direction between the continuous measurements of the output value consistent with each other. Although researchers don’t check that all observed conclusions, obtained by different observers, different reasonable ways and different the objective facts, are consistent if researchers do not know the objective facts, researchers can at least check whether all observed conclusions obtained by both different observers and different ways are consistent or not. Some of them will be not the objective facts if they are not consistent. In other words, always the repeatability can be checked. In order to check the objective consistency, if researchers do not know the objective facts, researchers have to check whether the way researchers deal with data being objective consistency or not. The way is reasonable if researchers check a lot of times by simulation, according to the third party standard. Reproducibility also make the mean smaller difference between the mathematical measuring systems and the mathematical measuring conditions if the reasonable ways include many environmental conditions.
The analysis conclusion of non-authigenic logic is not relevant to the mathematical scholars. That is to say, no matter what mathematical scholars, according to the similar mathematical data, adopted with the reproducibility of statistic in Mathematics methods, analysis of the conclusion must be the similar to each other. This is because, the problem of a mathematical study has nothing to do with mathematical scholars, just is the only objective of law science.
Both the objective consistency and the repeatability are called reproducibility (再现性).
Third is how to keep continuously developing as the default rule (默认规则). It means that the implied terms of the rule before there is not new information are legal and can ensure the normal operation of a mathematical complex system. In other words, always respect the original hypothesis (尊重原假设). Everything is right in the world (存在的就是合理的)! The default rule is the fact that is one of the most reproducibility methods. Respect the default rule, can guarantee the things on the basis of the reproducibility being to keep continuously developing. According to the rule of the default, any default method to deal with problems, the principle of no violation, is preconception.
The default rule should be as complete as possible. In no other intervention conditions, the default rule can make the mathematical complex system running normally. For the complete default rule, researchers should strictly abide by as much as possible. If a mathematical researcher first has obtained the observations of some data of the object of study, non-authigenic logic will think that this data is a true reflection of the research object, the other data should be repeated observations of these data, so with the same type and form (reproducibility). The analysis conclusion of non-authigenic logic, in the data to the form of a limited number, will stabilize. At this time, must ensure no relationship between the analysis conclusion and the number of data of a small amount of increase and decrease.
What the “The first impression is strongest” is the thinking way for the “fire” properties of a steady multilateral system imitating a mathematical complex system, and to consider the controlling-development problems. It belongs to the Fire (
) subsystem of the mathematical complex system since it controls the fluctuations of the mathematical complex system under the condition of a lot of unknown disturbances, which is the development and growth stage of all things, just like in the Summer of a year. In the initial stage of development of a mathematical complex system, under the condition of maintaining the status quo, the greatest possible to control interference, stable and free development, the purpose is to make a mathematical complex system can quickly grow. In order to explain the growth state of all things must be in the absence of disturbance assumptions, with the above ways of thinking, to control the fluctuations of the mathematical complex system first. The fluctuations have nothing to do with the observer behavior, and only related to the growth state of the mathematical complex system. Only in this way, can understand the growth cause of a mathematical complex system, get real Fire (
) properties of a mathematical complex system, and get the most development goals.
Under the principle of preconception, the articles can refer to see Zhang & Mao (2004), Feng et al. (2005), Zhang et al. (2005), Pan et al. (2008b), Chen et al. (2009b) and Luo et al. (2010a). #
(c) Earth (
): Integration coordination combination principle (整体协调化合原则)
The integration coordination combination principle is based on the overall nature of the problem, highlighting the overall structure of the analysis of a problem and transform, found that the problem of overall structural characteristics, is good at from the view of “integration”, put some formula or graph as a whole, grasp the correlation between them, purposeful and conscious processing as a whole. For example, integration thought method is in the algebraic expression of reduction and evaluated, equation (group), geometric solution certificate, etc., are widely used. Integration substitution, the superimposed fold by processing, the overall operation, assumes that the argument as a whole, fill in the whole processing, geometry shape, and so on, all is the whole idea concrete application of the method in solving mathematical complex system problems.
The integration coordination combination principle contains three aspects: one is how to think as the searching null composition rule (零成分搜索规则). This is able to find the composition which has nothing to do with a mathematical complex system as a whole, also called searching null composition capability (零成分搜索能力). In the affairs of human knowledge as a whole, it is difficult to realize the internal structure of things as a whole, can’t distinguish who good who bad internal things. However, the human is able to distinguish between what has nothing to do with the whole thing? These things which have nothing to do with the things as a whole are called things zero composition as a whole. Adhere to the zero component search thinking, can ensure that the observation of the whole is correct and objective. Follow zero component search rule, the proposed any an observation of knowledge and the method of doing things, is not in violation of the principle of integration coordination combination.
Holistic thinking in TCP or TCMath allows us to deal with a mathematical complex system is not managed to seize the main factors of it, but tried to find itself has nothing to do with this mathematical complex system of interference factors, and try to clear them out of the mathematical complex system itself. This is because any an internal factor of the mathematical complex system, in some cases, is likely to be important factors. When a mathematical complex system runs by balance and stability, any a way of strengthening some factors or degradation of some factors by mathematical researchers may be harmful for mathematical complex systems. For a social complex system, for example, if researchers eliminate all the criminals (“evil”), then the police system (“the vital chi”) will not exist, because the police system (“the vital chi”) is by eliminating the criminal system (the “evil”) to survival. Again for a cancer patient as a medicine complex system, for example, if researchers eliminate all of the cancer cells (the “evil”), then all the white blood cells (“the vital chi”) will not exist, because in TCP or TCMath’ concept, white blood cells (“the vital chi”) are by eating cancer cells (the “evil”) to live. It can be done only to run the social complex system of various energy channels, makes the harmful energy (“evil”) can’t gather together and make good energy (“the vital chi”) to eliminate harmful energy (the “evil”) to survival. To increase the ability of the police system or to acupuncture a cancer patient, for example, is suitable method of integration, and is to get rid of the interference factors. People can bear a little significant factor as a significant factor to deal with, but can’t bear a significant factor for processing as a non-significant factor. This method is called as “zero component search” in the TCP or TCMath.
Second is how to do as the integration rule (整合规则). This is able to integrate many small problems into a handful of a big problem, also called integration capability (整合能力). Mankind observes things as a whole can do to put the small overall combination into a larger whole. Only adhere to the integration rule, can guarantee to have something done as a whole. Follow the integration rule, any an integration method of doing things, is not in violation of the principle of integration coordination combination.
The integration coordination combination principle is also due to that one doesn’t have to look at the collection
of the research objects, in which
can be classified into
, but to focus on how to promote the overall coordination of the scale rapid combined mathematical complex system? First of all, the integration capability will guarantee that is able to integrate many small problems into a handful of a big problem. Integration job in the integration theory plays an extremely important role in the position. If there is no integration, so the global idea will not be able to be gotten, a mathematical complex system capacity will not be able to realize overall understanding of, which will cause the integration work being not for a whole.
Third is how to keep continuously developing as the decomposition rule (分解规则). This is able to have a big problem into several small problems, also called the decomposition capability (分解能力). Only one had the capacity to the overall decomposition of the things, he can continue in-depth development of the whole things gradually. Follow the rule of decomposition, the proposed any decomposition method and the understanding of details are not in violation of the principle of integration coordination combination.
The decomposition capability will guarantee that is able to break down into several parts of a whole. The decomposition job in the integration theory plays an extremely important role in the position. If there is no decomposition, so the integration work will not be able to restore, a mathematical complex system capacity will not be able to realize automation, which will cause the integration work is not for a long time.
The principle of integration coordination combination is the thinking way for the “earth” properties of a steady multilateral system imitating a mathematical complex system, and to consider the problems of combination to produce results. It belongs to the Earth (
) subsystem of the mathematical complex system since it makes the coordination of the center and fluctuation in the mathematical complex system which is the scale development continuously and combined stage of all things, just like in the Long-Summer of a year. In the long-term combined development stages of a mathematical complex system, the purpose of both eliminating irrelevant factors interference and realizing the coordinated development is to make a mathematical complex system can realize the balanced development of the most stable and can combine to produce results. In order to explain the combined stage of all things, people must be in the absence of combined assumptions, with the above ways of thinking, to make the coordination of the center and fluctuation of all subsystems in the mathematical complex system first. The coordination has nothing to do with the observer behavior, and only related to the combined state of the mathematical complex system. Only in this way, can people understand the combination cause of a mathematical complex system, get real Earth (
) properties of a mathematical complex system, and get the most combined goals.
Under the principle of integration coordination combination, the articles can refer to see Wang et al. (2017a, 2017b) and Zhang et al. (2007). #
(d) Metal (
): Logic layering principle (逻辑分层原则)
“Logic layering principle” has another name is: Heaven and People as a whole (天人合一). Heaven, is the nature; People, is human; Nature and humanity as a whole, is the mutual understanding, friendship, by using the same logic-analysis structure in a different level of.
This logic layering principle contains three aspects: one is how to think as the Global-Local thinking rule (从整体到局部思维). There are both the Global logic for a large mathematical complex system and the Local logic for its subsystems. Their logic structures are the same. However the Local subject or logic is restrained by the Global logic and the Global logic contains and restrains the Local logic. The Global logic can solve the problems for the Local logic, but not always the Local logic solves the problems for the Global logic. The idea is also called logic downward compatibility (逻辑向下兼容能力). Only keep from Global to Local thinking, can guarantee to the thing won’t appear a large deviation of the understanding of the way, can logically guarantee to realize the objective laws of things. Follow from the Global to Local thinking, any one of the proposed knowledge of things as a whole and local, is not in violation of the principle of logic layering.
One of the basic requirements of logic reasoning must be compatible with down, it’s like computer high version of the software must be able to handle it the low version of the software problems. The current level of logic of a mathematical complex system must apply to the logic of its subsystems. Otherwise, the entire logic structure will be chaos. Low level logic, of course, can’t deal with some high-level logic problems. The rule requiring people’s mind should be from Global to Local, rather than the opposite. Because from the Global to Local thinking is unique, its uniqueness can guarantee the reproducibility of reasoning conclusion. But from the Local to Global thinking, the way may be varied. Because there is no uniqueness of thinking, the reproducibility can not be guaranteed. By the Global to Local thinking, the main problem of Mathematics is not to reduce dimension analysis, but is to improve dimensional analysis. Because only increase dimensional analysis, possible to master a Global logic, with the conclusion of Global reproducibility.
Second is how to do as the logic causal cycle rule (逻辑因果圈). It is also called the logic causal chain (逻辑因果链). That is to say, any a logic idea makes some logic, and is made by some logic; any a logic idea restrains some logic, and is restrained by some logic: i.e., one logic idea overcomes another logic idea and one logic idea is overcome by another logic idea. In other words, any a logic idea is a certain logic analysis of cognitive level or watching layer by researchers. Only adhere to the rule of logic causal circle, can guarantee to any an understanding of things, people have done some things. Follow the rule of logic causal circle, any one of the proposed causal problems and the methods of dealing with the causal are not in violation of the principle of logic layering.
Logic layering principle is also due to that one doesn’t have to look at the collection
of the research objects, in which
can be classified into
, but to focus on how to get the biggest reward for mathematical complex systems? First of all, anyone’s ability is limited, he used a logic can only apply to his observes corresponding to a level of a mathematical complex system. To believe in it the logic conclusion of also only applies to the corresponding level, in big ways, he is always conditioned by a large mathematical complex system of logic, in small ways, it also can take smaller any a mathematical complex system logic completely clear. In general, a large mathematical complex system logic subject is a logic coarsening of its some small mathematical complex systems. Absolutely don’t put any a logic idea as the king, and admits that it is used in a certain level, it is the basic ways of dealing with problems of non-authigenic logic.
Third is how to keep continuously developing as the seriousness of logic rule (逻辑的严肃性规则). It is that any a logic must at least satisfy the uniqueness, hereditary, reversibility, reasoning ability and associative law. In other words, any a logic system must be of a multilateral system (多边系统). Only adhere to the seriousness of logic rule, can trust to ensure that the correct logic reasoning conclusion, make the logic reasoning method and the conclusion, continue to exist for a long time. Follow the seriousness of logic rule, any a proposed by logic reasoning method and the conclusion, is not in violation of the principle of logic layering.
A logic idea is the law of thinking, a logic theory is the theory about law of thinking. Sometimes both logic and logic theory are the same. As the law of thinking, the uniqueness, hereditary, reversibility, reasoning ability and associative law are the basic conditions of a reasoning logic. The reasoning ability can make the logic workable. The uniqueness and associative law of logic are to ensure that the inference conclusion by different logic reasoning has the reproducibility. The hereditary of logic is to ensure that the reasoning conclusion by different logic reasoning in the corresponding logic analysis level can be long-term survival and genetic. The reversibility of logic is to ensure that the reasoning conclusion by different logic reasoning conforms to the cultural characteristics of human beings. For example, the statements of both “A can launch B” and “B can be launched from A” are completely equivalent description in human culture. But from the point of relation theory, these are the two reversible relations to each other. The reversibility of logic is to ensure that the two relations reasoning are equivalent. From this idea, it is found that any a logic system must be of a multilateral system.
The logic layering principle is the thinking way for the “metal” properties of a steady multilateral system imitating a mathematical complex system, and to consider the problems of getting-results as far as possible. It belongs to the Metal (
) subsystem of the mathematical complex system since it makes the deviation between the real center of a mathematical complex system and the expected goal of researchers smaller, which is the getting-results and accepted stage of all things, just like in the Autumn of a year. Receiving phase in a mathematical complex system, namely, a preliminary systematic risk, the mathematical complex system is to obtain the biggest harvest in order to make it can realize the biggest function ability. In order to explain the accepted stage of all things, people must be in the absence of accepted assumptions, with the above ways of thinking, to make the deviation between the real center of a mathematical complex system and the expected goal of researchers smaller first. The deviation has nothing to do with the observer’s behavior, and only related to the accepted state of the mathematical complex system. Only in this way, can people understand the accepted cause of a mathematical complex system, get real Metal (
) properties of a mathematical complex system, and get the most accepted goals.
Under the principle of logic layering, the articles can refer to see Zhang (2006, 2007b), Zhang et al. (1999, 2011), Luo et al. (2010b), Wu et al. (2012), Liao et al., (2012), Lin et al. (2015) and Wang et al. (2010, 2011a, 2011b). #
(e) Water (
): Automation principle (自动化原则)
“Automation principle” has another name: by doing nothing, everything is done (无为而无不为). It means to believe that mathematical complex systems have themselves long-term survival genetic ability, as far as possible to protect and use this ability to achieve the purpose of people needs.
This principle contains three aspects: one is how to think as the intervention reaction rule (干预响应规则). This is to believe any a mathematical complex system having intervention reaction ability (干预响应能力). With an automating ability, there must be a kind of force, this force for the intervention of the outside world, can produce an internal reaction. This internal reaction is: the subsystem of the mathematical complex system, which has a loving relationship with the intervention mathematical complex subsystem, and the intervention force same direction of change; the subsystem of the mathematical complex system, which has a killing relationship with the intervention subsystem, and the intervention of external force changes in the opposite direction. Only by insisting on intervention reaction of thought premise, to ensure the intervention has the possibility of an automatic operation. Following the intervention reaction rule, any one of the proposed method to deal with problems related to the intervention reaction and knowledge, is not in violation of the principle of automation.
The automation principle is also due to that one doesn’t have to look at the collection
of the research objects, in which
can be classified into
, but to focus on how to protect the long-term genetic survival of a mathematical complex system’s ability to fight the biggest risk? First of all, in order to allow us to get the goal of TCP or TCMath, only a mathematical complex system must be able to response mankind intervention, so people can make the mathematical complicated system difficult to do an intervention of. It is believed that a mathematical complex system has the ability to response the intervention of TCP or TCMath, otherwise the system will be a simple system. The scope of simple system is not the study of TCP or TCMath. As a mathematical complex system is done an intervention of it by an external force, the mathematical complex system able to take advantage of the external force to change itself, this ability is called the intervention reaction ability. Generally speaking, the intervention reaction ability is stronger if more use it. As far as possible the intervention reaction ability of a mathematical complex system is used to solve the problems of TCP or TCMath, it is one of the basic ideas of non-authigenic.
Second is how to do as the self-protection rule (自保护规则). Any a mathematical complex system is believed having self-protection ability (自保护能力). Self-protection ability is believed that by the intervention system has the ability to make the worst-hit subsystem restorable ability. Only insist on the self-protection rule, believe the intervention system can protect themselves, all things as far as possible let the intervention system on themselves to do. In this way, it is to ensure that TCP or TCMath has something done in the automatic operation. Follow the rule of self-protection, have put forward anything related to the self-protection and the method to deal with problems, is not in violation of the principle of automation.
A mathematical complex system is able to exist because it already exists. A mathematical complex system has been believed in its ability to maintain its existence or to restore its normal state. This ability is called the self-protection ability. When a mathematical complex system appears crisis or unstable, the mathematical complex system can use its self-protection ability to maintain the balance of its existence or to make the mathematical complex system restorable. If a mathematical complex system can response the human mathematical intervention, TCP or TCMath should make full use of this intervention in the mathematical complex system to increase its self-protection ability. Generally speaking, the self-protection ability is stronger if more use it. As far as possible the self-protection ability of a mathematical complex system is used to solve the problems of TCP or TCMath, it is one of the basic ideas of non-authigenic.
Third is how to keep continuously developing as the second physiologic system rule (第二生理系统规则). In order to ensure the operation of the whole can be automated, things must make it in the first physiologic system, there is a first physiologic system in the second run. The second physiologic systems control the first physiologic system. In the first physiologic system during a normal operation, it attains the energy from the first physiologic systems. When the first physiologic system is during an abnormal operation, the second physiologic system is to afford the energy for the first physiologic system, in order to ensure the normal operation of the first physiologic systems. The second physiologic system to effectively control the first physiologic system, it must have a great strength. The macro in the first physiologic systems is a generic and must be variable, called a macro variable. Any a mathematical complex system has relatively constants or macro variables. It can carry out the macro substitution of macro variables. A mathematical complex system can change the macro variable values, and achieve the purpose of the programming in order to maintain its system balance. The idea is called the macro substitution ability (宏替换能力) or the genetic ability (遗传能力). Only by insisting on the second physiologic system rule, it is to ensure that system can run normally, and continue to genetic. Follow the rule of physiologic system, any a proposed and the second physiologic systems related knowledge and processing the second physiologic system related method, are not in violation of the principle of automation.
An intervention response capability or a self-protection capability of a mathematical complex system is how to implement? Within it there must be a kind of parameters. These parameters are constants in a state. By changing the constants, the mathematical complex systems will be arrived in another state. The parameters in the field of computer artificial intelligence logic are called macro variables. The mathematical complex system can automatically change the macro variable values, making it automatically to the next state. The meaning of automation ability is to a mathematical complex system can change by itself. It can increase its intervention response ability by itself, and it can realize its self-protection ability by itself. Macro variables are important factors of resistance biggest risk such that the mathematical complex system can survive long genetic automatically. In order to control the mathematical complex system service for human, the key is to find the corresponding macro variables.
Automation principle is the thinking way for the “water” properties of a steady multilateral system imitating a mathematical complex system, and to consider the problems of the biggest risk resistance making genetic survive for a long time. It belongs to the Water (
) subsystem of the mathematical complex system since it makes the risk loss between each observed data of a mathematical complex system and the expected goal of researchers smaller, which is the risk and hiding stage of all things, just like in the Winter of a year. The purpose of both against the biggest risk and achieving long-term hidden is to make a mathematical complex system can genetic survive for a long time. In order to explain the hiding stage of all things, TCP or TCMath must be in the absence of hiding assumptions, with the above ways of thinking, to make the risk loss between each observed data of a mathematical complex system and the expected goal of researchers smaller first. The risk loss has nothing to do with the observer’s behavior, and only related to the hiding state of the mathematical complex system. Only in this way, can TCP or TCMath understand the hiding cause of a mathematical complex system, get real Water (
) properties of a mathematical complex system, and get the most hiding goals.
Under the principle of automation, the articles can refer to see Zhang et al. (1998), Pan et al. (2008a), Chen et al. (2009a), Zhang & Zhao (2018), Bai, et al. (2021) and Luo & Zhang (2016). #
All in all, the five subsets
’s of a Wu-Xing Model do not mean the five elements (metal, wood, water, fire and earth), but with the philosophical meaning of five aspects corresponding to the five subsets
’s.
In above philosophical meaning of all five aspects (wood (
), fire (
), earth (
), metal (
), water (
)) of non-authigenic logic, both wood (
) and earth (
) are the most basic aspects since they can at least ensure that the mathematical complex system exists to begin and combines to produce results. This condition is a necessary condition to ensure the existence of the system.
In above philosophical meaning of all five aspects (wood (
), fire (
), earth (
), metal (
), water (
)) of non-authigenic logic, the three subsystems of wood (
), earth (
) and water (
) are the most completely aspects since they can ensure that the mathematical complex system runs normally. This condition is a sufficient condition to ensure the running of the system.
In above philosophical meaning of all five aspects (wood (
), fire (
), earth (
), metal (
), water (
)) of non-authigenic logic, the subsystem of fire (
) is the most important aspect since it contains a subsystem that plays a leading role, which is called the Jun-fire subsystem. In addition to the xiang-fire (
) subsystem, the other parts protect the jun-fire (
) system, manage and coordinate the relationship between the other subsystems of the system and jun-fire (
) subsystem of the system, and perform the basic functions of the normal fire system. This condition is a sufficient and necessary condition to ensure the better running of the system. The subsystem .fire (
) = jun-fire (
)
xiang-fire (
) is called the heart zang-organ subsystem.
In above philosophical meaning of all five aspects (wood (
), fire (
), earth (
), metal (
), water (
)) of non-authigenic logic, there are the loving relationship: wood (
)
fire (
)
earth (
)
metal (
)
water (
); and the killing relationship: wood (
)
earth (
)
water (
)
fire (
)
metal (
). General close is loving, alternate is killing.
All these conclusions of non-authigenic logic can be summarized in Table 2. #
3.2. The Negative Philosophical Answer of Hilbert Sixth Mathematical Conjecture
One of the most famous is Hilbert’s sixth mathematical conjecture of his 23 mathematical conjecture problems. Hilbert’s sixth mathematical conjecture problem said, “the axiomatization of physics plays an important role in mathematics”.
Theorem 3.1.There is no an axiomatic system which makes that all branches of physics can be axiomatic. #
Remark 1. People build an Axiom system, first of all, to observe the research object, found some real objective facts and put these a few real objective facts, summarizes become generally accepted an axiom system. But the idea violates the non-authigenic thinking rule of the principle of no assumption as one of rules of the non-authigenic logic. This is because non-authigenic logic can not be related to the research object. Human beings are unable to determine the objective facts of true and false. Only through a relationship is to identify the objective fact is good for mankind. #
Remark 2. People build an Axiom system, first observed the objective facts of different due to different people, can put forward different axiom hypothesis. But the idea violates the reproducibility rule of the principle of preconception as one of rules of the non-authigenic logic. The rule of the reproducibility contains objective rule of consistency and repeatability. If researchers allow different people using different Axiom systems, there are the rule of repetitive problems. There is only one objective fact. Two different processing methods of the axiom system of at least one are not reasonable. If researchers don’t allow different people using different Axiom systems, so objective consistency and repeatability as reproducibility checking can be a problem. Because the mankind is unable to determine the objective facts of true and false, it is whether can only judge for their own. #
Remark 3. People build an Axiom system, cannot be in fully understand the whole details of the research object, to establish a basic right of an Axiom system. This is because the human beings cannot understand the whole details of a mathematical complex system. Can only be observed whether things related to the research object, and only confirm the thing has nothing to do with the whole. For things related to the overall level, but it is difficult to identify. So that to establish a system of axioms, it is in violation of the searching null composition thinking rule of the principle of integration coordination combination as one of rules of the non-authigenic logic. #
Remark 4. To establish an axiomatic system is the logic foundation of western science. Had the axiomatic system, human beings have to distinguish the standard proposition and theorem of true and false. And an axiomatic system has compatibility relation proposition and the theorem is the true proposition. Do not have the compatibility relation proposition is false propositions. Judge true and false proposition logic is the logic foundation of western science. This logic is called the formal logic. But the formal logic is in violation of logical seriousness rule of the logic layering principle as one of rules of the non-authigenic logic.
In accordance with the logic seriousness rule: any a logic idea must at least satisfy the uniqueness, hereditary, reversibility, reasoning ability and associative law. But, Zhang & Shao (2012) show that the true or false proposition logic can not meet the needs of associative law. That is to say: the true or false proposition logic reasoning can not meet the needs of associative law between three false propositions. In addition, it also can be proved that the formal logic does not meet the uniqueness of reasoning, hereditary of reasoning, and so on. This shows that: the logic basis of the formal logic is a more seriousness problem. Only in a formal logic Axiom system, carries on the compatibility between the true proposition reasoning.
People build an Axiom system, to serve the formal logic reasoning. If the formal logic reasoning needs to change, people’s building the Axiom system itself is not necessary. #
Remark 5. Once an Axiom system is established, then axiom system is not changed. What things can’t be changed may be true, but the mathematical complex things are in change forever, in changing, the Axiom system is not the same. Mankind is the best way of doing things, is not set up any an Axiom system, and should make a mathematical complex system of the second physiologic systems manage their own. By the fact, so say: building an Axiom system violates both the self-protection and the second physiologic system rules of the automation principle as two of rules of the non-authigenic logic. #
4. The Negative Mathematical Answer of Hilbert Sixth Mathematical Conjecture
For example, in the true and false binary of proposition logic, the associative law of reasoning does not hold since
The reason is that the true and false binary of proposition logic is not the generalized relationship reasoning. But if the true and false binary of proposition logic can be changed into the generalized relationship reasoning, the reasoning of the true and false binary of proposition logic as the formal logic is not still to satisfy the multilateral system reasoning model. It is proved by using the reduction to absurdity.
If there is an axiom system which allows for all branches of the physical system being established, so, for the axiom system, the relationship between the proposition and the axiom system can only be the compatible and incompatible relations. Write the compatible proposition as 0, and write the incompatible proposition as 1. The axiom system of all research propositions space of theTao model can be written for