1. Introduction and Overview
We present a study of coherent active-sterile neutrino oscillations as a possible source of baryogenesis via leptogenesis. Consider a reaction of the form
that produces a lepton asymmetry that is partially converted to a baryon asymmetry before the sphaleron freeze-out temperature
[1]. The present baryon-to-photon ratio of the universe is measured to be
[2]. Let us consider a bench-mark scenario with all numbers calculated at a reference temperature
. We define the electron asymmetry
, and similarly for
,
and
.
is the number density of electrons. The asymmetry at
from neutrino oscillations required to obtain
is
[3]. At
the age of
the universe is
, and the time between collisions of active neutrinos in the reaction
is
, where
is the cross-section. We note that at
neutrinos are of short wavelength relative to
, i.e.
.
Observed neutrino oscillations require that at least two neutrino eigenstates have mass. To this end, we add at least
gauge singlet Weyl_R neutrinos
to the Standard Model. To obtain lepton number violation, we assume the neutrinos are of the Majorana type, i.e. we add both Dirac and Majorana mass terms to the Lagrangian [4].
Let us consider the reaction
, with neutrino mass eigenstates
oscillating coherently during time
. The condition for coherent oscillations is that
has mass
. (The physics described in this overview will be developed in the following Sections.) The cross-section for the lepton number violating reaction is reduced relative to the lepton conserving reaction by a factor
due to polarization miss-match, where
is the neutrino eigenstate mass, and E is the neutrino energy in the laboratory frame.
One mechanism to obtain CP violation is to have two interfering amplitudes with different “strong” phases and different “weak” phases [5]. A “strong” phase (the name is borrowed from B-physics) is a phase that does not change sign under CP-conjugation. A “weak” phase changes sign under CP-conjugation. Here, the “weak” phases are the CP-violating phases in the weak mixing matrix U. The “strong” phases are the propagation phases of the interfering ultra-relativistic neutrinos,
, with energy
, and
. To obtain a sizable CP violation asymmetry, the relative propagation phase difference
between two neutrinos in time
should be of order
or less. This requires two neutrinos to satisfy
.
There are cosmological constraints, mainly from Big Bang Nucleosynthesis (BBN), that require the mass of sterile neutrinos to be
. Thus, the interesting mass range for sterile neutrinos contributing to leptogenesis is approximately 0.14 GeV to 1.1 GeV.
From the following studies, we conclude that nature may have added, to the Standard Model, two or more gauge singlet Weyl_R Majorana neutrinos, with fine tuned parameters, as the source of neutrino masses and mixing, and successful baryogenesis via leptogenesis. This scenario is not new, yet is not mentioned in several leading leptogenesis reviews. Here, we emphasize analytic solutions, and an understanding of several delicate issues related to Majorana neutrinos, lepton number violation, CP-violation, polarization miss-match, and coherence. In the following Sections, we develop, step-by-step, the physics behind the preceding comments.
2. Dirac Neutrinos
In the following sections we consider a neutrino experiment with a source at the origin of coordinates, and a detector at a distance
. We assume
, so the neutrinos are almost on mass-shell.
is the neutrino momentum. At first let us consider a single neutrino flavor, and the reaction
.
Before electroweak symmetry breaking (EWSB) at
[1], the neutrino field
is massless, carries the 2-dimensional “Weyl_L” representation of the proper Lorentz group, and satisfies the wave equation
(1)
where
,
,
, and
are the Pauli matrices [4]. Summation over repeated indices is understood.
, and
. Multiplying on the left by
, obtains the Klein-Gordon wave equation of a massless field:
(2)
where
is the metric.
After EWSB the Higgs boson acquires a vacuum expectation value
[4]. The field
forward scatters on
with amplitude
becoming a
(
is a Yukawa coupling [4] ), that forward scatters on
with amplitude
becoming a
, etc. The field
transforms as “Weyl_R” [4]. These scatterings are forward because
does not depend on the space-time coordinates
. These scatterings are described by the Dirac equation,
(3)
with
. In this way the field
is created (arguably) after EWSB, on a time scale 1/m, and the fields
and
couple together forming a 4-dimensional field
that carries the reducible Dirac = Weyl_L
Weyl_R representation of the proper Lorentz group. The solution of (3) proportional to
, in a Weyl basis, is [4]
(4)
corresponding to a particle of mass m, and momentum
with
. This is the “stepping stone” mechanism of mass generation [6]. Alternatively, consider (3): the
creates
on a time scale 1/m, which in turn creates
, etc. Solutions for other
can be obtained with Lorentz transformations.
and
are complex numbers that define the polarization of the neutrino (to be discussed in Section 5).
The solution of (3) proportional to
is
(5)
The charge conjugate of
is [4]
(6)
Note that
transforms as Weyl_L, while
transforms as Weyl_R [4].
,
,
, and
are scalars with respect to the proper Lorentz group. The Dirac Equations (3) can be summarized as
. We work in the Weyl basis with
matrices
(7)
The Weyl_L and Weyl_R projectors are
, and
. For example, the Weyl_L component of
is
. Note that W± and Z only “see” the Weyl_L fields
or
. Neutrinos may, or may not, have a conserved
charge q such as lepton number. In quantum field theory, the fields are interpreted as follows:
•
creates a particle with charge +q, and spin angular momentum component
with amplitude
, and
with amplitude
;
•
annihilates this particle;
•
creates an antiparticle with charge -q, and spin
with amplitude
, and
with amplitude
;
•
annihilates this antiparticle.
This interpretation is needed to avoid unstable particles with negative energy. These particles and antiparticles have mass m, spin
, positive energy E, and momentum
. Note that antiparticles have the opposite charge of the corresponding particle.
Let us now consider two neutrino flavors,
and
. The field
may forward scatter on
with amplitude
becoming a
, which may forward scatter on
with amplitude
becoming a
, etc. As a result, two mass eigenstates acquire masses:
(8)
(9)
For simplicity, we have suppressed the sub-indices u for neutrinos, or v for anti-neutrinos. For example, the interaction
producing a weak state has
,
, and
is normalized to 1. An observation at distance L obtains
with probability
, or
with probability
, where
(10)
with
, and
. This is the phenomenon of neutrino oscillations.
3. Majorana Neutrinos
If neutrinos have no additive conserved charge (such as lepton number), it is possible to add Majorana type mass terms to (3):
(11)
(12)
(13)
(14)
Here, with one generation, the masses can be made real by re-phasing the fields. The charge conjugate fields are
,
,
, and
. Majorana mass terms for fields
are not added, at tree level, because such terms are not gauge invariant. Note that the Majorana mass terms link
with
, etc. Then, a created
may forward scatter on
(with amplitude
) becoming a
, that may forward scatter on
(whatever it is, e.g. a dimension 5 operator containing
) becoming a
, that may forward scatter on
(with amplitude
) becoming a
, etc, see Figure 1. Equations (13) and (14) are the charge conjugate of Equations (11) and (12), respectively.
Note that before EWSB, the fields
and
are in statistical equilibrium due to their interactions with the gauge bosons
and B. From (11) to (14) we conclude that after EWSB, the fields
,
,
, 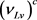 , and their conjugates, become linked together so that the Majorana character of neutrinos may emerge dynamically after EWSB on a time scale 1/m (for the case of interest
, and their conjugates, become linked together so that the Majorana character of neutrinos may emerge dynamically after EWSB on a time scale 1/m (for the case of interest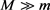 ).
).
Equations (11) to (14) are linear and homogeneous, and their general solution is a superposition of mass eigenstates. Each term of (11) transforms as Weyl_L, and is proportional to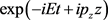 , and so they may be mixed. Equations (11) can be re-written as
, and so they may be mixed. Equations (11) can be re-written as
 (15)
(15)
Equations (12) can be re-written as
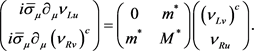 (16)
(16)
Both (15) and (16) can be diagonalized simultaneously with a unitary matrix U and its complex-conjugate to obtain the equation in the mass eigenstate basis:
 (17)
(17)
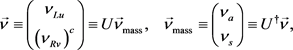 (18)
(18)
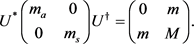 (19)
(19)
The unitary matrix U that satisfies (15), (17), and (19), with real and positive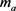 ,
, 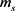 , and M, is
, and M, is
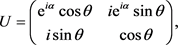 (20)
(20)
where![]() ,
, ![]() , and
, and![]() . The eigenvalues are
. The eigenvalues are
![]() (21)
(21)
From here on we take the Majorana masses![]() , so
, so![]() . Then
. Then ![]() is an “active” neutrino that is mostly
is an “active” neutrino that is mostly![]() , while
, while ![]() is a “sterile” neutrino that is mostly
is a “sterile” neutrino that is mostly![]() .
.
According to (18), the fields evolve as follows:
![]() (22)
(22)
Consider a source that produces neutrinos in a weak state, e.g.![]() . At the source,
. At the source, ![]() and
and ![]() is normalized to 1. Define
is normalized to 1. Define![]() . We obtain
. We obtain
![]() (23)
(23)
The lepton violating reaction has probability ![]() that differs from
that differs from ![]() by polarization miss-match factors (to be discussed in Section 5):
by polarization miss-match factors (to be discussed in Section 5):
![]() (24)
(24)
The interpretation of these equations is discussed in Section 4.
Let us generalize to ![]() generations of weak
generations of weak ![]() doublets, and
doublets, and ![]() gauge singlet Weyl_R neutrinos. We introduce the notation
gauge singlet Weyl_R neutrinos. We introduce the notation
![]() (25)
(25)
These fields are related to the mass eigenstates as follows:
![]() (26)
(26)
The ![]() weak mixing matrix U is unitary:
weak mixing matrix U is unitary:![]() ,
,![]() . The generalization of (15) is
. The generalization of (15) is
![]() (27)
(27)
![]() is the complex
is the complex ![]() Dirac mass matrix, and M is the symmetric
Dirac mass matrix, and M is the symmetric ![]() Majorana mass matrix chosen real. The symmetric mass matrix is diagonalized as follows:
Majorana mass matrix chosen real. The symmetric mass matrix is diagonalized as follows:
![]() (28)
(28)
The masses ![]() of the mass eigenstates are chosen real and positive. The fields
of the mass eigenstates are chosen real and positive. The fields ![]() evolve as (22). Then, for ultra-relativistic neutrinos, the probability of a lepton conserving event, e.g.
evolve as (22). Then, for ultra-relativistic neutrinos, the probability of a lepton conserving event, e.g.![]() , is [2]
, is [2]
![]() (29)
(29)
![]() (30)
(30)
where![]() . The sums in (29) are over mass eigenstates
. The sums in (29) are over mass eigenstates ![]() with masses
with masses ![]() and
and ![]() that cannot be discriminated in the experiment, and are coherent, see Section 6. Under CP conjugation,
that cannot be discriminated in the experiment, and are coherent, see Section 6. Under CP conjugation,![]() . The first two terms on the right hand side of (29), denoted
. The first two terms on the right hand side of (29), denoted![]() , are CP conserving, while the last term, denoted
, are CP conserving, while the last term, denoted![]() , may be CP violating. Note that to obtain CP violation, at least one physical phase in U is needed, in addition to the propagation phase
, may be CP violating. Note that to obtain CP violation, at least one physical phase in U is needed, in addition to the propagation phase ![]() (that requires
(that requires![]() ). Since U is unitary,
). Since U is unitary,![]() .
.
The probability to observe a lepton violating event, e.g.![]() , is
, is
![]() (31)
(31)
![]() (32)
(32)
where we have included the polarization miss-match factors discussed in Section 5. The probability ![]() for the CP-conjugate event, e.g.
for the CP-conjugate event, e.g.![]() , is obtained by
, is obtained by![]() . Note that the first two terms, denoted
. Note that the first two terms, denoted![]() , violate lepton number but conserve the CP symmetry. Note that the last term, denoted
, violate lepton number but conserve the CP symmetry. Note that the last term, denoted![]() , is lepton number violating and may be CP violating, and is the source of the leptogenesis studied in this article. Considering the width of the neutrino energy distribution, strong CP violation requires
, is lepton number violating and may be CP violating, and is the source of the leptogenesis studied in this article. Considering the width of the neutrino energy distribution, strong CP violation requires![]() . The last two terms in (29) and (31) are due to coherent interference of the mass eigenstates.
. The last two terms in (29) and (31) are due to coherent interference of the mass eigenstates.
Note that for![]() ,
, ![]() is proportional to the square of the “effective mass”
is proportional to the square of the “effective mass”![]() . Neutrino-less double beta decay experiments constrain the effective mass of electrons to be less than 0.165 eV [2].
. Neutrino-less double beta decay experiments constrain the effective mass of electrons to be less than 0.165 eV [2].
Equations (29) and (31) assume neutrinos are nearly on mass shell, i.e.![]() , and that the neutrino mean energy
, and that the neutrino mean energy![]() . The sums in these equations only include neutrinos that are coherent, see Section 6.
. The sums in these equations only include neutrinos that are coherent, see Section 6.
4. Interpretation
In a neutrino oscillation experiment, most neutrinos traverse the detector without interacting. In the limit![]() ,
,![]() . The probabilities
. The probabilities ![]() are defined as the number of
are defined as the number of ![]() counts at the far detector, divided by the number of
counts at the far detector, divided by the number of ![]() counts at the near detector, corrected for acceptance and detector efficiencies. If the efficiency of the detector for
counts at the near detector, corrected for acceptance and detector efficiencies. If the efficiency of the detector for ![]() is negligible,
is negligible, ![]() may still be “measured” as a disappearance in the sum of other channels. For the probability
may still be “measured” as a disappearance in the sum of other channels. For the probability![]() , the detector efficiency factor due to polarization miss-match has already been included.
, the detector efficiency factor due to polarization miss-match has already been included.
The interpretation of the preceding equations needs an understanding of the entire experiment. In particular we need to consider polarization miss-match (Section 5), and coherence (Section 6). If at the source the neutrino mass is sufficiently uncertain, then a weak state is produced, i.e. a coherent superposition of mass eigenstates. If at the source the neutrino mass is sufficiently well determined, then a mass eigenstate is produced. Even if the neutrino mass eigenstates are produced coherently, they may lose coherence before being detected, either in transit, and/or at the detector. If this is the case, then an “observation” has been made, and we need to pass from amplitudes to probabilities, i.e. interference terms are lost.
For simplicity, we consider a single generation, i.e. (15) to (24). If production is coherent, and the mass eigenstates have become incoherent, then the probability for ![]() is
is![]() , and the probability for
, and the probability for ![]() is
is![]() . In the case of coherent production and incoherent detection, e.g. the neutrino mass is measured at the detector with a resolution sufficient to discriminate between
. In the case of coherent production and incoherent detection, e.g. the neutrino mass is measured at the detector with a resolution sufficient to discriminate between ![]() and
and![]() , the combined probability to have a
, the combined probability to have a ![]() and a lepton conserving event
and a lepton conserving event ![]() is
is![]() , the combined probability to have a
, the combined probability to have a ![]() and a lepton conserving event is
and a lepton conserving event is![]() , the combined probability to have a
, the combined probability to have a ![]() and a lepton violating event
and a lepton violating event ![]() is
is![]() , and the combined probability to have a
, and the combined probability to have a ![]() and a lepton violating event is
and a lepton violating event is![]() . The factor
. The factor ![]() is due to polarization miss-match (Section 5) that reduces the cross-section by this factor, and applies to a real, i.e. finite extent, unpolarized detector. We assume
is due to polarization miss-match (Section 5) that reduces the cross-section by this factor, and applies to a real, i.e. finite extent, unpolarized detector. We assume ![]() and
and![]() . E is the energy of the neutrino in the laboratory frame, i.e. the detector.
. E is the energy of the neutrino in the laboratory frame, i.e. the detector.
The case of interest to the leptogenesis scenario studied in this article is coherent production and coherent detection, since interference is needed for CP violation. If production is coherent, and the mass eigenstates remain coherent at detection, then ![]() of (23) is the probability to observe the lepton conserving event
of (23) is the probability to observe the lepton conserving event![]() . In any practical neutrino oscillation experiment, with a finite detector,
. In any practical neutrino oscillation experiment, with a finite detector, ![]() of (24) is the probability to observe the lepton violating event
of (24) is the probability to observe the lepton violating event![]() .
.
5. Polarization Miss-Match
Consider the decay ![]() in the rest frame of
in the rest frame of![]() . The neutrino
. The neutrino ![]() carries the field
carries the field![]() , see (4). Let
, see (4). Let ![]() be the angle between the
be the angle between the ![]() spin and the
spin and the ![]() momentum. Then
momentum. Then ![]() and
and ![]() [4]. Therefore, the amplitude for
[4]. Therefore, the amplitude for ![]() to create a right-handed (i.e. helicity +1/2)
to create a right-handed (i.e. helicity +1/2) ![]() is
is![]() , and the amplitude to create a left-handed
, and the amplitude to create a left-handed ![]() is
is![]() . Helicity is the projection of the spin angular momentum in the direction of the momentum, i.e.
. Helicity is the projection of the spin angular momentum in the direction of the momentum, i.e.![]() . Note that most ultra-relativistic
. Note that most ultra-relativistic ![]() are left-handed.
are left-handed.
Consider the CP-conjugate decay ![]() in the rest frame of
in the rest frame of![]() . The anti-neutrino
. The anti-neutrino ![]() carries the field
carries the field![]() , see (6). Let
, see (6). Let ![]() be the angle between the
be the angle between the ![]() spin and the
spin and the ![]() momentum. Then
momentum. Then ![]() and
and![]() . Therefore, the amplitude for
. Therefore, the amplitude for ![]() to create a right-handed (i.e. helicity +1/2)
to create a right-handed (i.e. helicity +1/2) ![]() is
is![]() , and the amplitude to create a left-handed
, and the amplitude to create a left-handed ![]() is
is![]() . Note that most ultra-relativistic
. Note that most ultra-relativistic ![]() are right-handed.
are right-handed.
Note that for ultra-relativistic Majorana neutrinos we can still distinguish neutrinos (lepton number ≈+1 and helicity ≈−1/2) from anti-neutrinos (lepton number ≈−1 and helicity ≈+1/2), since lepton number is conserved to a high degree of accuracy, see Section 10 for a numerical example.
Consider the lepton-conserving sequence of events ![]() followed by
followed by![]() . We assume
. We assume ![]() and
and![]() . The probability, after averaging over
. The probability, after averaging over ![]() and
and![]() , is
, is![]() , where
, where ![]() is the amplitude corresponding to mass eigenstate i, and
is the amplitude corresponding to mass eigenstate i, and ![]() is the angle with respect to the final
is the angle with respect to the final![]() . Consider the lepton-violating sequence of events
. Consider the lepton-violating sequence of events ![]() followed by
followed by![]() . The probability, after averaging over
. The probability, after averaging over ![]() and
and![]() , is
, is![]() . The probability for the lepton conserving events (29) is normalized to
. The probability for the lepton conserving events (29) is normalized to![]() , so the relative polarization miss-match factor for lepton violating events is
, so the relative polarization miss-match factor for lepton violating events is![]() . This factor has been included in (24) and (31). We note that in the limit
. This factor has been included in (24) and (31). We note that in the limit![]() , the experimental distinction between Dirac and Majorana neutrinos fades away, and lepton violation vanishes.
, the experimental distinction between Dirac and Majorana neutrinos fades away, and lepton violation vanishes.
6. Coherence
The sums in (29) and (31) only include coherent neutrinos. To obtain coherent oscillations between two neutrinos of masses ![]() and
and ![]() it is necessary that the energy uncertainty
it is necessary that the energy uncertainty ![]() of the produced and detected neutrinos be sufficiently large, i.e.
of the produced and detected neutrinos be sufficiently large, i.e.![]() , where
, where ![]() [7]. If this condition is met, what is created is a flavor eigenstate, i.e. a coherent superposition of mass eigenstates, and oscillations remain coherent while the wave packets of the two components overlap. The overlap ceases after the “coherence time” [7]
[7]. If this condition is met, what is created is a flavor eigenstate, i.e. a coherent superposition of mass eigenstates, and oscillations remain coherent while the wave packets of the two components overlap. The overlap ceases after the “coherence time” [7]
![]() (33)
(33)
where ![]() is the Gaussian wave packet duration. The combined coherence factor after time
is the Gaussian wave packet duration. The combined coherence factor after time ![]() is [7]
is [7]
![]() (34)
(34)
In the present application we take, arguably, ![]() ,
, ![]() , and
, and![]() , where
, where ![]() is the mean time for a neutrino to collide with a charged lepton. Consider the reference temperature
is the mean time for a neutrino to collide with a charged lepton. Consider the reference temperature![]() , and
, and![]() . The cross-section
. The cross-section ![]() for
for ![]() is given by (50.25) of [2]. We obtain
is given by (50.25) of [2]. We obtain![]() , where
, where ![]() is the electron number density at
is the electron number density at![]() . Consider an active-sterile neutrino oscillation with
. Consider an active-sterile neutrino oscillation with![]() . Requiring coherent oscillations,
. Requiring coherent oscillations, ![]() obtains the bound
obtains the bound![]() . For
. For![]() ,
, ![]() corresponds to
corresponds to![]() . Therefore, for
. Therefore, for![]() , oscillations remain coherent for
, oscillations remain coherent for![]() . We verify also that
. We verify also that![]() , with
, with![]() , so the neutrinos of interest are nearly on mass shell.
, so the neutrinos of interest are nearly on mass shell.
7. Asymmetry Build-Up
So far we have been studying a neutrino oscillation experiment with baseline L. In this Section we apply the results to the universe when it has the reference temperature![]() . Consider a single
. Consider a single![]() . The
. The ![]() lifetime is
lifetime is![]() . The probability that the interaction
. The probability that the interaction ![]() occurs in the time interval from t to
occurs in the time interval from t to ![]() is
is![]() . The lepton number violating and CP violating asymmetry,
. The lepton number violating and CP violating asymmetry, ![]() , is proportional to t for the case of interest
, is proportional to t for the case of interest![]() . The mean of
. The mean of ![]() is then
is then![]() .
.
Consider the contribution of the channel ![]() to
to![]() . Let
. Let ![]() be the comoving number density of
be the comoving number density of ![]() at time
at time![]() , where
, where![]() . Then, at time
. Then, at time![]() ,
,
![]() (35)
(35)
Taking the difference of these two equations, and dividing by ![]() , obtains
, obtains
![]() (36)
(36)
Summing over ![]() and
and ![]() obtains
obtains
![]() (37)
(37)
The last term is the “wash-out” term that tends to restore the equilibrium value![]() . Note that
. Note that ![]() decreases by
decreases by ![]() in time
in time ![]() until it reaches either
until it reaches either
![]() (38)
(38)
or until wash-out sets in at
![]() (39)
(39)
We note that ![]() and
and ![]() are proportional to
are proportional to ![]() if
if![]() , so, in this case of interest,
, so, in this case of interest, ![]() and
and ![]() are independent of
are independent of![]() .
.
8. Constraints from Cosmology
Constraints from Big Bang Nucleosynthesis (BBN), Baryon Acoustic Oscillations (BAU), and direct searches, limit the mass of sterile neutrinos to be greater than 0.14 GeV [8], so the interesting sterile neutrino mass range, for the leptogenesis scenario being considered, is approximately 0.14 GeV to 1.1 GeV. The lifetimes of these neutrinos range from approximately 10−5 s at![]() , to 0.1 s for
, to 0.1 s for ![]() [8].
[8].
Big Bang Nuleosynthesis and cosmic microwave background (CMB) measurements do not allow one additional ultra-relativistic degree of freedom at ![]() [2]. For the Standard Model, the equivalent number of neutrinos (for BBN) is
[2]. For the Standard Model, the equivalent number of neutrinos (for BBN) is ![]() [2]. The Planck CMB result gives
[2]. The Planck CMB result gives ![]() at 95% confidence [2]. So an extra stable neutrino, that was once in statistical equilibrium with the Standard Model sector, needs to decouple at
at 95% confidence [2]. So an extra stable neutrino, that was once in statistical equilibrium with the Standard Model sector, needs to decouple at![]() , where
, where ![]() is the confinement-deconfinement temperature. Such an extra neutrino contributes ≤0.12 to
is the confinement-deconfinement temperature. Such an extra neutrino contributes ≤0.12 to![]() . Therefore, sterile neutrinos either 1) never reached statistical equilibrium with the Standard Molel sector, or 2) reached statistical equilibrium, but decoupled at
. Therefore, sterile neutrinos either 1) never reached statistical equilibrium with the Standard Molel sector, or 2) reached statistical equilibrium, but decoupled at ![]() and hence are sufficiently cooler than active neutrinos at
and hence are sufficiently cooler than active neutrinos at ![]() [2], or 3) the sterile neutrino mass is
[2], or 3) the sterile neutrino mass is ![]() and these neutrinos decayed before T reached
and these neutrinos decayed before T reached![]() .
.
As an example, for![]() , and
, and ![]() in the range of interest 0.14 GeV to 1.1 GeV, we find that sterile neutrinos never reach statistical equilibrium with the Standard Model sector, or reach equilibrium but decouple at
in the range of interest 0.14 GeV to 1.1 GeV, we find that sterile neutrinos never reach statistical equilibrium with the Standard Model sector, or reach equilibrium but decouple at![]() , and hence do not affect BBN.
, and hence do not affect BBN.
9. Leptogenesis with ![]() and
and ![]()
Let us study the simplest case with lepton number violation and CP violation. We take ![]() generations of active neutrinos and
generations of active neutrinos and ![]() gauge singlet Weyl_R neutrinos. For
gauge singlet Weyl_R neutrinos. For ![]() and
and![]() , the unitary mixing matrix U from (28), to order
, the unitary mixing matrix U from (28), to order![]() , is
, is
![]() (40)
(40)
and the mass eigenstates are
![]() (41)
(41)
![]() (42)
(42)
![]() (43)
(43)
The active neutrino mass![]() , and sterile neutrino masses
, and sterile neutrino masses ![]() and
and ![]() are real and positive. The Dirac terms
are real and positive. The Dirac terms ![]() and
and ![]() are complex.
are complex.
Let us write (38) for the present case![]() ,
,![]() . To order
. To order ![]() we obtain
we obtain
![]() (44)
(44)
This equation assumes the approximation ![]() valid for
valid for![]() , corresponding to masses
, corresponding to masses![]() . The three terms correspond to interference of neutrinos
. The three terms correspond to interference of neutrinos![]() ,
, ![]() , and
, and![]() , respectively. We find that all terms of order
, respectively. We find that all terms of order ![]() cancel. In conclusion, if both sterile neutrinos have masses in the approximate range 0.14 to 1.1 leptogenesis is negligible.
cancel. In conclusion, if both sterile neutrinos have masses in the approximate range 0.14 to 1.1 leptogenesis is negligible.
Let us consider the case![]() , and
, and ![]() so that
so that ![]() is incoherent. In this case we keep only the first term in (44). Leptogenesis can be successful if we are able to find
is incoherent. In this case we keep only the first term in (44). Leptogenesis can be successful if we are able to find ![]() and
and ![]() that satisfy (41) and (44) (omitting the terms with
that satisfy (41) and (44) (omitting the terms with![]() ) with the required
) with the required![]() . Note that (41) and (44) are under-constrained: they have multiple solutions. We therefore use the Casas-Ibarra procedure [9], and write the solution to (41) in the form
. Note that (41) and (44) are under-constrained: they have multiple solutions. We therefore use the Casas-Ibarra procedure [9], and write the solution to (41) in the form![]() , where R is any orthogonal, i.e.
, where R is any orthogonal, i.e.![]() ,
, ![]() matrix. In the present case
matrix. In the present case
![]() (45)
(45)
Substituting in (44) we obtain
![]() (46)
(46)
As an example, we take![]() ,
, ![]() , and
, and![]() . Also
. Also![]() , and
, and![]() . We obtain
. We obtain ![]() . A solution then needs fine tuning, e.g.
. A solution then needs fine tuning, e.g.
![]() (47)
(47)
where![]() . Since we have chosen
. Since we have chosen![]() , wash-out remains negligible.
, wash-out remains negligible.
Equation (44) can be generalized to ![]() by inspection.
by inspection.
10. Leptogenesis with ![]() and
and ![]()
Without loss of generality we work in a basis that diagonalizes the ![]() charged lepton mass matrix, and the
charged lepton mass matrix, and the ![]() Majorana mass matrix M. The
Majorana mass matrix M. The ![]() weak mixing matrix U, defined in (28), to lowest order in
weak mixing matrix U, defined in (28), to lowest order in![]() , has the form [2]
, has the form [2]
![]() (48)
(48)
To the present order of approximation, we take![]() . The 3 × 3 PMNS weak mixing matrix of active neutrinos
. The 3 × 3 PMNS weak mixing matrix of active neutrinos ![]() depends on three angles and one Dirac CP-violating phase
depends on three angles and one Dirac CP-violating phase![]() , that have been measured, and two Majorana CP-violating phases
, that have been measured, and two Majorana CP-violating phases ![]() and
and ![]() (with the notation of [2] ) that have not been measured. Unphysical phases of
(with the notation of [2] ) that have not been measured. Unphysical phases of![]() , that can be canceled by re-phasing fields, have already been fixed. We take the central measured values of these parameters for normal (NO) or inverse (IO) neutrino mass ordering from the first column of Table 14.7 of [2]. The two active neutrino mass-squared differences are also obtained from this Table.
, that can be canceled by re-phasing fields, have already been fixed. We take the central measured values of these parameters for normal (NO) or inverse (IO) neutrino mass ordering from the first column of Table 14.7 of [2]. The two active neutrino mass-squared differences are also obtained from this Table. ![]() and
and ![]() are free parameters until measured. Neutrino oscillation experiments show that at least 2 neutrino eigenstates have mass, so (arguably) at least
are free parameters until measured. Neutrino oscillation experiments show that at least 2 neutrino eigenstates have mass, so (arguably) at least ![]() gauge singlet Weyl_R neutrinos need to be added to the Standard Model. For the case
gauge singlet Weyl_R neutrinos need to be added to the Standard Model. For the case![]() , the lightest active neutrino mass is zero. For the case
, the lightest active neutrino mass is zero. For the case![]() , the lightest active neutrino mass is a free parameter until measured.
, the lightest active neutrino mass is a free parameter until measured.
The diagonal mass matrix of active neutrinos, obtained from (28) and (48), is [2]
![]() (49)
(49)
Successful leptogenesis is possible if we are able to solve (49), (38), and (39) with the needed lepton asymmetry![]() . We focus on the case
. We focus on the case![]() . The problem is under-constrained, so again we follow the Casas-Ibarra procedure [9]. From (49), with the notation
. The problem is under-constrained, so again we follow the Casas-Ibarra procedure [9]. From (49), with the notation![]() , we obtain
, we obtain ![]() with
with![]() . Finally,
. Finally,
![]() (50)
(50)
where R is any orthogonal, i.e.
![]() (51)
(51)
![]() matrix. Equation (49) is satisfied by (50). To satisfy (38), the matrix R needs to be complex.
matrix. Equation (49) is satisfied by (50). To satisfy (38), the matrix R needs to be complex.
Successful leptogenesis requires fine tuning of the unknown parameters. As a proof of principle we present the following example: normal neutrino mass ordering, ![]() ,
, ![]() , and
, and![]() . We also set
. We also set![]() ,
, ![]() , and
, and![]() , and note that the results depend negligibly on these last three parameters (for the texture of the matrix R chosen below). At
, and note that the results depend negligibly on these last three parameters (for the texture of the matrix R chosen below). At![]() , the age of the universe is
, the age of the universe is![]() , and
, and![]() . Equation (51) has many solutions. Successful leptogenesis needs
. Equation (51) has many solutions. Successful leptogenesis needs ![]() and
and ![]() imaginary to high accuracy, as in (47). To obtain a solution that satisfies
imaginary to high accuracy, as in (47). To obtain a solution that satisfies ![]() we choose a particular texture of R (that makes the results insensitive to
we choose a particular texture of R (that makes the results insensitive to![]() ), and obtain:
), and obtain:
![]() (52)
(52)
with![]() . The probabilities for a “neutrino oscillation experiment” with
. The probabilities for a “neutrino oscillation experiment” with![]() , from terms in (29) and (31) are respectively:
, from terms in (29) and (31) are respectively:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (53)
(53)
We note that the lepton number violating reactions are suppressed with respect to the lepton conserving ones, and the CP violating terms are suppressed with respect to the CP conserving ones. We note that the terms ![]() are of order 10−12 and positive, while the terms
are of order 10−12 and positive, while the terms ![]() are of order 10−18 and can be positive or negative.
are of order 10−18 and can be positive or negative.
From the first term in ![]() we obtain the effective mass of neutrino-less double beta decay experiments for this example:
we obtain the effective mass of neutrino-less double beta decay experiments for this example:![]() . The current limit is 0.165 eV [2].
. The current limit is 0.165 eV [2].
Asymmetries per channel are presented in Table 1 (from (38) and (39) without the sums over ![]() and
and![]() ). Note that, in this example, we do not reach saturation due to wash-out, i.e.
). Note that, in this example, we do not reach saturation due to wash-out, i.e. ![]() in each channel. Summing the asymmetries in the last row of Table 1 obtains
in each channel. Summing the asymmetries in the last row of Table 1 obtains ![]() as required. In conclusion, successful baryogenesis via leptogenesis may be achieved with the fine-tuning shown in (52), plus the fine tuning of the masses (so that the positive and negative terms in the last sum of (39) cancel to one part in 102).
as required. In conclusion, successful baryogenesis via leptogenesis may be achieved with the fine-tuning shown in (52), plus the fine tuning of the masses (so that the positive and negative terms in the last sum of (39) cancel to one part in 102).
Several tests with modifications of this example follow:
• Setting![]() , or
, or![]() , or
, or![]() , obtains
, obtains ![]() as before, so the CP-violating phases in the PMNS matrix
as before, so the CP-violating phases in the PMNS matrix ![]() contribute negligibly to leptogenesis (in this scenario of active-sterile neutrino oscillations). Leptogenesis is mostly due to the CP-violating asymmetries in R, or equivalently
contribute negligibly to leptogenesis (in this scenario of active-sterile neutrino oscillations). Leptogenesis is mostly due to the CP-violating asymmetries in R, or equivalently![]() .
.
• Choosing a real R obtains![]() , so, again, the Dirac phase
, so, again, the Dirac phase ![]() of
of ![]() contributes negligibly to leptogenesis.
contributes negligibly to leptogenesis.
• Setting ![]() and a real R obtains
and a real R obtains![]() , as expected. This cross-check is satisfied for 0, 1, 2 or 3 coherent sterile neutrinos.
, as expected. This cross-check is satisfied for 0, 1, 2 or 3 coherent sterile neutrinos.
• Setting![]() , to test a case with one coherent sterile neutrino, obtains
, to test a case with one coherent sterile neutrino, obtains ![]() and
and![]() . Note that wash-out dominates.
. Note that wash-out dominates.
• Setting![]() ,
, ![]() and
and![]() , to test a case with three coherent neutrinos, obtains
, to test a case with three coherent neutrinos, obtains ![]() and
and![]() . Note that the signs are now wrong, and wash-out dominates.
. Note that the signs are now wrong, and wash-out dominates.
• Results for inverse neutrino mass ordering are similar. However, we were unable to reach successful leptogenesis, i.e.![]() .
.
11. Sterile Neutrino Dark Matter?
Detailed dark matter properties have recently been obtained by fitting spiral galaxy rotation curves, and, independently, by fitting galaxy stellar mass distributions [10]. These measurements imply that dark matter was in thermal and diffusive equilibrium with the Standard Model sector in the early universe, and decoupled (from the Standard Model sector and from self-annihilation) at a temperature![]() . If dark matter particles are fermions, the measurements obtain their mass
. If dark matter particles are fermions, the measurements obtain their mass ![]() [10]. This mass is disfavored by the Tremaine-Gunn limit (that applies to fermion dark matter) [11], which however needs revision [12] [13] [14] [15]. Fermion dark matter is also disfavored, relative to boson dark matter, by spiral galaxy rotation curves and by galaxy stellar mass distributions with a significance of
[10]. This mass is disfavored by the Tremaine-Gunn limit (that applies to fermion dark matter) [11], which however needs revision [12] [13] [14] [15]. Fermion dark matter is also disfavored, relative to boson dark matter, by spiral galaxy rotation curves and by galaxy stellar mass distributions with a significance of ![]() [10].
[10].
Nevertheless, let us see if sterile neutrinos of mass ![]() could have reached statistical equilibrium with the Standard Model sector by the time of the confinement-deconfinement temperature
could have reached statistical equilibrium with the Standard Model sector by the time of the confinement-deconfinement temperature![]() . This is the minimum temperature at which dark matter in equilibrium with the Standard Model sector can decouple without spoiling the agreement with Big-Bang Nucleosynthesis. At this temperature the age of the universe is
. This is the minimum temperature at which dark matter in equilibrium with the Standard Model sector can decouple without spoiling the agreement with Big-Bang Nucleosynthesis. At this temperature the age of the universe is![]() , and the neutrino lifetime is
, and the neutrino lifetime is![]() . The number of baryons per electron is
. The number of baryons per electron is![]() . The number
. The number ![]() of sterile neutrinos of mass
of sterile neutrinos of mass ![]() that need to be produced per electron is
that need to be produced per electron is![]() . (We use the standard notation in cosmology [2].) For
. (We use the standard notation in cosmology [2].) For![]() , i.e. from (23), we obtain
, i.e. from (23), we obtain ![]() (for
(for![]() ), insufficient to produce the observed density of dark matter (as reported in [16] ).
), insufficient to produce the observed density of dark matter (as reported in [16] ).
Let us consider![]() . The example of Section 10 has the matrix R with a texture that makes the results insensitive to
. The example of Section 10 has the matrix R with a texture that makes the results insensitive to![]() . We may set
. We may set ![]() with no significant change in the results reported in Section 10. For that fine-tuned example we obtain from (29), before subtracting reverse conversions,
with no significant change in the results reported in Section 10. For that fine-tuned example we obtain from (29), before subtracting reverse conversions,
![]() (54)
(54)
The sub-index “6” stands for ![]() with mass
with mass![]() . Reverse conversion limits these numbers to the statistical equilibrium value 1. In conclusion, sufficient sterile neutrino dark matter production is possible. Such dark matter is disfavored by observations but not ruled out.
. Reverse conversion limits these numbers to the statistical equilibrium value 1. In conclusion, sufficient sterile neutrino dark matter production is possible. Such dark matter is disfavored by observations but not ruled out.
12. Sterile Neutrino Search?
Consider a neutrino experiment that reconstructs the detected neutrinos in all-charged final states with the capability to discriminate a sterile neutrino mass from the active neutrino masses. In this case there is no interference, and the probability to detect the sterile neutrino![]() , relative to the probability to detect any neutrino in the
, relative to the probability to detect any neutrino in the ![]() channel is
channel is
![]() (55)
(55)
with no sum implied. For![]() , i.e. from (20), we obtain
, i.e. from (20), we obtain ![]() , which is experimentally hopeless. For
, which is experimentally hopeless. For ![]() and
and![]() , i.e. from (40), we obtain
, i.e. from (40), we obtain![]() , which is very interesting! For the example in Section 9 we obtain
, which is very interesting! For the example in Section 9 we obtain![]() , which is less hopeless. For
, which is less hopeless. For![]() , and the example in Section 10, we obtain
, and the example in Section 10, we obtain![]() , where “4” stands for
, where “4” stands for ![]() of mass
of mass![]() . This is the maximum for all channels, and is experimentally challenging. A search for sterile neutrinos in the approximate mass range 0.14 GeV to 2.0 GeV may be considered. A study has been presented in [17]. In conclusion, the same factor
. This is the maximum for all channels, and is experimentally challenging. A search for sterile neutrinos in the approximate mass range 0.14 GeV to 2.0 GeV may be considered. A study has been presented in [17]. In conclusion, the same factor ![]() that makes the model fine-tuned, enters to the fourth power, and may allow the model to be tested experimentally!
that makes the model fine-tuned, enters to the fourth power, and may allow the model to be tested experimentally!
13. Conclusions
We have studied coherent active-sterile neutrino oscillations as a possible source of leptogenesis. To this end, we add ![]() gauge invariant Weyl_R neutrinos to the Standard Model with both Dirac
gauge invariant Weyl_R neutrinos to the Standard Model with both Dirac ![]() and Majorana M mass terms. We find that for
and Majorana M mass terms. We find that for ![]() we can obtain the measured active neutrino masses and mixings, and successful baryogenesis via leptogenesis, with, however, the fine tuning described in Sections 9 and 10, see (47) and (52). The Dirac CP-violating phase
we can obtain the measured active neutrino masses and mixings, and successful baryogenesis via leptogenesis, with, however, the fine tuning described in Sections 9 and 10, see (47) and (52). The Dirac CP-violating phase![]() , and Majorana CP-violating phases
, and Majorana CP-violating phases ![]() and
and ![]() of the 3 × 3 PMNS weak mixing matrix
of the 3 × 3 PMNS weak mixing matrix ![]() contribute negligibly to this scenario of leptogenesis. The major contribution comes from the phases of the Dirac mass matrix
contribute negligibly to this scenario of leptogenesis. The major contribution comes from the phases of the Dirac mass matrix ![]() that links the Weyl_L and Weyl_R neutrinos. The Dirac nature of charged particles and the possible Majorana nature of neutrinos, emerge dynamically after electroweak symmetry breaking, i.e. just before sphaleron freeze-out. The possible Majorana nature of neutrinos allows lepton number violation, with, however, a cross-section reduced by a factor
that links the Weyl_L and Weyl_R neutrinos. The Dirac nature of charged particles and the possible Majorana nature of neutrinos, emerge dynamically after electroweak symmetry breaking, i.e. just before sphaleron freeze-out. The possible Majorana nature of neutrinos allows lepton number violation, with, however, a cross-section reduced by a factor ![]() due to polarization miss-match. This penalty renders lepton number violation beyond the reach of current laboratory experiments. CP-violation is the result of coherent interference of neutrinos with two clashing phases: a phase from the weak mixing matrix U (mainly from the Dirac mass matrix
due to polarization miss-match. This penalty renders lepton number violation beyond the reach of current laboratory experiments. CP-violation is the result of coherent interference of neutrinos with two clashing phases: a phase from the weak mixing matrix U (mainly from the Dirac mass matrix![]() ), and a phase
), and a phase ![]() from neutrino propagation. The interference is coherent if the sterile neutrino mass
from neutrino propagation. The interference is coherent if the sterile neutrino mass ![]() is less than approximately 6 GeV. The condition
is less than approximately 6 GeV. The condition![]() , for strong CP violation, implies
, for strong CP violation, implies![]() . Constraints from Big Bang Nucleosynthesis require
. Constraints from Big Bang Nucleosynthesis require![]() . We find that at least one of the sterile neutrinos needs to have a mass in the approximate range 0.14 to 1.1 GeV to obtain successful leptogenesis.
. We find that at least one of the sterile neutrinos needs to have a mass in the approximate range 0.14 to 1.1 GeV to obtain successful leptogenesis.
With![]() , we may include in the model sterile neutrino dark matter with the measured mass
, we may include in the model sterile neutrino dark matter with the measured mass ![]() [10]. However, such dark matter is disfavored by observations (but not ruled out [10] ).
[10]. However, such dark matter is disfavored by observations (but not ruled out [10] ).
The present scenario of leptogenesis requires a fine tuning parameter![]() , and a pattern of R such as (52). Why should nature select such a pattern (reminiscent of patterns in chemistry and biology)? It is interesting to note that with this fine tuning parameter K, the neutrino Yukawa coupling magnitudes become comparable to the ones of charged leptons and quarks. It is also interesting to note that K may bring sterile neutrino search within experimental reach.
, and a pattern of R such as (52). Why should nature select such a pattern (reminiscent of patterns in chemistry and biology)? It is interesting to note that with this fine tuning parameter K, the neutrino Yukawa coupling magnitudes become comparable to the ones of charged leptons and quarks. It is also interesting to note that K may bring sterile neutrino search within experimental reach.
The scenario studied in this article is similar to the model νMSM [8], where calculations have been carried out numerically in full detail. The search for sterile neutrinos with ![]() with sufficient sensitivity may be possible in a dedicated experiment [17].
with sufficient sensitivity may be possible in a dedicated experiment [17].