A Small Correction to a Paper of Vandermonde

Matthew Davis, Shiv K. Gupta

Department of Mathematics, West Chester University of Pennsylvania, West Chester, PA 19383, USA.

DOI: 10.4236/ojdm.2021.112004                

Abstract

In this paper using elementary Galois Theory, we give a detailed explanation of the calculation of the radical expression for which was first discussed by Vandermonde decades before Galois and we point out and correct a minor correction in his work which was also observed by Lagrange.

Keywords

Cyclotomy, Galois, Galois Group, Gauss, Lagrange, Tignol, Vandermonde

1. Introduction

In an often-quoted impressive paper Vandermonde [1] comes very close to introducing the concept of Cyclotomy. Discussing the work of Vandermonde, Jean-Pierre Tignol [2] writes

∙∙∙The existence of a cyclic permutation that does preserve the relations (among the roots) is very remarkable; and quite mysterious property of cyclotomic equations, which should have to awaken Vandermonde’s curiosity. If he had investigated this property he could have developed the theory of cyclotomy about 30 years before Gauss.

The fact that Vandermonde did his investigations without the benefit of the knowledge of the work of Gauss (as Galois did) is indeed very noteworthy. His observation about the existence of cyclic permutation which preserves the relations among the roots is forerunner to the introduction of the concept of automorphism in later times. From Phillip S. Jones [3] we learn what Lebesgue thought about the work of Vandermonde.

∙∙∙Vandermonde’s real and unrecognized claim to fame was lodged in his first paper, in which he approached the general problem of the solvability of algebraic equations through a study of functions invariant under permutations of the roots of the equations.

Several overviews of Vandermonde’s algebraic work have already appeared in print. For an excellent account by Olaf Neumann see [4]. For a short biographical sketch of Vandermonde containing Lebesgue’s opinion about his work see Phillip S. Jones cited above.

In the last article of the aforementioned paper, Vandermonde talks about applying the theory developed earlier to solve (that is to find radical expressions for the roots of) the equation $z^{11}-1=0$, having disposed of the similar problems for $z^n-1=0$, for smaller values of n in the earlier articles of the same paper. In particular, he gives radical expressions for $2\cos \frac{2k\pi }{11}$ for $1\le k\le 5$ (actually for some unknown reasons Vandermonde prefers to work with the equation whose roots are $-2\cos \frac{2k\pi }{11}$ for $1\le k\le 5$ ). Vandermonde does not provide the details of his calculations—he only points out the method of doing so and gives the final result. Tignol [5] has reproduced the radical expressions for $-2\cos \frac{2k\pi }{11}$ for $1\le k\le 5$ as they appear in Vandermonde’s paper—still not providing any of the details which led him (or Vandermonde) to the radical expressions for $-2\cos \frac{2k\pi }{11}$ for $1\le k\le 5$. These radical expression for $-2\cos \frac{2k\pi }{11}$ for $1\le k\le 5$, given by Vandermonde and reproduced from there by Tignol are:

Let

$a=-2\cos \frac{2\pi }{11},b=-2\cos \frac{4\pi }{11},c=-2\cos \frac{6\pi }{11},d=-2\cos \frac{8\pi }{11},e=-2\cos \frac{10\pi }{11}$

then the values of $a\mathrm{,}b\mathrm{,}c\mathrm{,}d\mathrm{,}e$ are given by the following expression (with appropriate choice of fifth roots of unity)

$\frac{1}{5}\left[1+{\Delta }^{\prime }+{\Delta }^{″}+{\Delta }^{‴}+{\Delta }^{iv}\right]$

where

${\Delta }^{\prime }=\sqrt[5]{\frac{11}{4}\left(89+25\sqrt{5}-5\sqrt{-5+2\sqrt{5}}+45\sqrt{-5-2\sqrt{5}}\right)}$

${\Delta }^{″}=\sqrt[5]{\frac{11}{4}\left(89+25\sqrt{5}+5\sqrt{-5+2\sqrt{5}}-45\sqrt{-5-2\sqrt{5}}\right)}$

${\Delta }^{‴}=\sqrt[5]{\frac{11}{4}\left(89-25\sqrt{5}-5\sqrt{-5+2\sqrt{5}}-45\sqrt{-5-2\sqrt{5}}\right)}$

${\Delta }^{iv}=\sqrt[5]{\frac{11}{4}\left(89-25\sqrt{5}+5\sqrt{-5+2\sqrt{5}}+45\sqrt{-5-2\sqrt{5}}\right)}$

Despite our repeated efforts, we failed to verify the correctness of above expressions. We decided to evaluate the expressions for ${\Delta }^{\prime },{\Delta }^{″},{\Delta }^{‴}$ and ${\Delta }^{iv}$ ourselves using the reductions procedure indicated in Vandermonde’s paper and obtained the following values:

${{\Delta }^{\prime }}_c=\sqrt[5]{\frac{11}{4}\left(89+25\sqrt{5}-25\sqrt{-10+2\sqrt{5}}+20\sqrt{-10-2\sqrt{5}}\right)}$

${{\Delta }^{″}}_c=\sqrt[5]{\frac{11}{4}\left(89+25\sqrt{5}+25\sqrt{-10+2\sqrt{5}}-20\sqrt{-10-2\sqrt{5}}\right)}$

${{\Delta }^{‴}}_c=\sqrt[5]{\frac{11}{4}\left(89-25\sqrt{5}-25\sqrt{-10-2\sqrt{5}}-20\sqrt{-10+2\sqrt{5}}\right)}$

${\Delta }_c^{iv}=\sqrt[5]{\frac{11}{4}\left(89-25\sqrt{5}+25\sqrt{-10-2\sqrt{5}}+20\sqrt{-10+2\sqrt{5}}\right)}$

The contribution of Vandermonde to the solutions of equations predates the work of Lagrange on the same by some twenty years. The work of Vandermonde and the opinion of Lagrange about it have also been mentioned in the article by Robin Rider Hamburg [5]. Specifically, while discussing cyclotomic equation Lagrange [6] makes the following statement about solving the equation

$u^5+u^4-4u^3-3u^2+3u+1=0$

By taking u negatively, the signs of all even terms are changed, and we have the equation solved by Vandermonde. This author only gives the expression obtained as a result of his general method, without indicating the details of the operations by which he achieved it, and nobody after him has been concerned, as far as I know, with the verification of this result, which may have remained unknown.

which among other things essentially says that by replacing u by $-u$ one obtains the equation solved by Vandermonde, namely $u^5-u^4-4u^3+3u^2+3u-1=0$, and he does not know of anyone who has verified the results obtained by Vandermonde. In fact, Lagrange also carries out the same calculations. The values obtained by us are exactly the same as ones found by Lagrange so we have some reason to have confidence in the correctness of our calculations.

Although the values of ${\Delta }^{\prime },{\Delta }^{″},{\Delta }^{‴}$ and ${\Delta }^{iv}$ given by Vandermonde appear to be different from ours but surprisingly ${\Delta }^{‴}$ and ${\Delta }^{iv}$ are the same as our ${{\Delta }^{‴}}_c$ and ${\Delta }_c^{iv}$ respectively. This is so because

$-5\sqrt{-5+2\sqrt{5}}-45\sqrt{-5-2\sqrt{5}}=-25\sqrt{-10-2\sqrt{5}}-20\sqrt{-10+2\sqrt{5}}$

as can be easily verified.

Also as it has been pointed out by Lagrange that if in the expressions for ${\Delta }^{\prime }$ and ${\Delta }^{″}$ given by Vandermonde the quantities $\sqrt{-5+2\sqrt{5}}$ and $\sqrt{-5-2\sqrt{5}}$ are interchanged then these coincide with values obtained by him (and us as well) since

$-5\sqrt{-5-2\sqrt{5}}+45\sqrt{-5+2\sqrt{5}}=-25\sqrt{-10+2\sqrt{5}}+20\sqrt{-10-2\sqrt{5}}$.

2. Radical Expression for $2cos\frac{2\pi }{11}$ via Galois Theory

In the explanation that follows we shall substantially adhere to the notations used by Vandermonde and Tignol. However, at some places, we shall use the notions from elementary Galois Theory for the justification for some of the steps in the calculations.

We begin by considering the equation

$z^{11}-1=0$ (1)

Dividing the above by $z-1$ we get the equation

$z^{10}+z^9+z^8+z^7+z^6+z^5+z^4+z^3+z^2+z+1=0$ (2)

whose roots are

${\text{e}}^{\frac{2\pi ik}{11}}=\cos \frac{2\pi k}{11}+i\sin \frac{2\pi }{11},1\le k\le 10$

Dividing this equation by $z^5$ and making the substitution $z+\frac{1}{z}=y$ we get

$y^5+y^4-4y^3-3y^2+3y+1=0$ (3)

whose five roots are:

${\text{e}}^{\frac{2\pi ik}{11}}+{\text{e}}^{-\frac{2\pi ik}{11}}=2\cos \frac{2\pi k}{11},\text{for}1\le k\le 5.$

We would have preferred to work with Equation (3). However as indicated earlier, for some reasons Vandermonde replaces y by −x in (3). In order to provide a convenient comparison with Vandermonde’s calculations, we shall do likewise. So by replacing y by −x in (3) we get the equation

$x^5-x^4-4x^3+3x^2+3x-1=0$ (4)

whose five roots are: $-2\cos \frac{2\pi k}{11}$, for $1\le k\le 5$.

If we let $\alpha ={\text{e}}^{\frac{2\pi i}{11}}$, the mapping $\alpha \to {\alpha }^2$, which permutes the 10 roots of Equation (2) as

$\alpha \to {\alpha }^2\to {\alpha }^4\to {\alpha }^8\to {\alpha }^5\to {\alpha }^{10}\to {\alpha }^9\to {\alpha }^7\to {\alpha }^3\to {\alpha }^6\to \alpha$

gives a generator of the group of automorphism of the field $\mathbb{Q}\left(\alpha \right)$. The restriction of this mapping to the subfield $\mathbb{Q}\left(\cos \frac{2\pi }{11}\right)$ (its maximum real subfield) induces an automorphism of $\mathbb{Q}\left(\cos \frac{2\pi }{11}\right)$. To see the effect of this automorphism on $\mathbb{Q}\left(\cos \frac{2\pi }{11}\right)$ we write:

$a=-2\cos \frac{2\pi }{11}=-\left(\alpha +\frac{1}{\alpha }\right)=-\left(\alpha +{\alpha }^{10}\right)$

$b=-2\cos \frac{4\pi }{11}=-\left({\alpha }^2+\frac{1}{{\alpha }^2}\right)=-\left({\alpha }^2+{\alpha }^9\right)$

$c=-2\cos \frac{6\pi }{11}=-\left({\alpha }^3+\frac{1}{{\alpha }^3}\right)=-\left({\alpha }^3+{\alpha }^8\right)$

$d=-2\cos \frac{8\pi }{11}=-\left({\alpha }^4+\frac{1}{{\alpha }^4}\right)=-\left({\alpha }^4+{\alpha }^7\right)$

$e=-2\cos \frac{10\pi }{11}=-\left({\alpha }^5+\frac{1}{{\alpha }^5}\right)=-\left({\alpha }^5+{\alpha }^6\right)$

Consider the tower of fields:

The automorphism of the field $\mathbb{Q}\left(\alpha \right)$ given by $\alpha \to {\alpha }^2$ induces an automorphism of its subfield $\mathbb{Q}\left(\cos \frac{2\pi }{11}\right)$ which cyclically permutes the five roots of (3) as follows:

$\begin{array}{l}\alpha +{\alpha }^{-1}\to {\alpha }^2+{\alpha }^{-2}\to {\alpha }^4+{\alpha }^{-4}\to {\alpha }^8+{\alpha }^{-8}\to {\alpha }^5+{\alpha }^{-5}\\ \to {\alpha }^{10}+{\alpha }^{-10}=\alpha +{\alpha }^{-1}\end{array}$

or

$2\cos \frac{2\pi }{11}\to 2\cos \frac{4\pi }{11}\to 2\cos \frac{8\pi }{11}\to 2\cos \frac{6\pi }{11}\to 2\cos \frac{10\pi }{11}\to 2\cos \frac{2\pi }{11}$

which is the same as

$a\to b\to d\to c\to e\to a$

In other words, the cyclic permutation $\left(a\mathrm{,}b\mathrm{,}d\mathrm{,}c\mathrm{,}e\right)$ preserves the (rational) relations among the roots of Equation (3). In the words of Tignol

Vandermonde’s brilliant (but not quite explicit) observation is that the permutation $a\to b\to d\to c\to e\to a$ preserves the relations between the roots.

As ${\left(\alpha +{\alpha }^{-1}\right)}^2={\alpha }^2+{\alpha }^{-2}+2$, we have $a^2=-b+2$ (which is same as $\cos \frac{4\pi }{11}=2{\cos }^2\frac{2\pi }{11}-1$ ). Applying the permutation $\left(a\mathrm{,}b\mathrm{,}d\mathrm{,}c\mathrm{,}e\right)$ to the relation

$a^2=-b+2$

we get

$b^2=-d+2$

(which is the same as $\cos \frac{8\pi }{11}=2{\cos }^2\frac{4\pi }{11}-1$ ).

Also as

$\left(\alpha +\frac{1}{\alpha }\right)\cdot \left({\alpha }^2+\frac{1}{{\alpha }^2}\right)=\left({\alpha }^3+\frac{1}{{\alpha }^3}\right)+\left(\alpha +\frac{1}{\alpha }\right)$

which is the same as saying

$2\cos \frac{2\pi }{11}\cdot 2\cos \frac{4\pi }{11}=2\cos \frac{6\pi }{11}+2\cos \frac{2\pi }{11}$

or

$a\cdot b=-a-c$

which is one of the 15 relations (among $a\mathrm{,}b\mathrm{,}c\mathrm{,}d$ and e) that Vandermonde indicates for the process of reduction (to be explained soon). The following is an easily verifiable list of relations among $a\mathrm{,}b\mathrm{,}c\mathrm{,}d$ and e given by Vandermonde

$\begin{array}{llll}{a}^2=-b+2\hfill & a\cdot b=-a-c\hfill & b\cdot c=-a-e\hfill & c\cdot d=-a-d\hfill \\ b^2=-d+2\hfill & a\cdot c=-b-d\hfill & b\cdot d=-b-e\hfill & c\cdot e=-b-c\hfill \\ c^2=-e+2\hfill & a\cdot d=-c-e\hfill & b\cdot e=-c-d\hfill & d\cdot e=-a-b\hfill \\ d^2=-c+2\hfill & a\cdot e=-d-e\hfill & \hfill & \hfill \\ e^2=-a+2\hfill & \hfill & \hfill & \hfill \end{array}$

Since the permutation $\left(a\mathrm{,}b\mathrm{,}d\mathrm{,}c\mathrm{,}e\right)$ induces the permutations

$a\cdot b\to b\cdot d\to d\cdot c\to c\cdot e\to e\cdot a\to a\cdot b$

$a\cdot c\to b\cdot e\to d\cdot a\to c\cdot b\to e\cdot d\to a\cdot c$

all the 15 relations among $a\mathrm{,}b\mathrm{,}c\mathrm{,}d$ and e given by Vandermonde can be derived by applying the permutation $\left(a\mathrm{,}b\mathrm{,}d\mathrm{,}c\mathrm{,}e\right)$ to each of the following three relations,

$a^2=-b+2,a\cdot b=-a-c,a\cdot c=-b-d$

It can be easily seen that any polynomial in $a\mathrm{,}b\mathrm{,}c\mathrm{,}d$ and e with rational coefficients can be reduced to a linear polynomial in the same by using the 15 relations among them given by Vandermonde. We refer to this procedure as the process of reduction.

Let $\omega ={\text{e}}^{\frac{2\pi i}{5}}=\cos \frac{2\pi }{5}+i\sin \frac{2\pi }{5}$ be a primitive fifth root of unity. It is easy to see that

$\cos \frac{2\pi }{5}=\frac{-1+\sqrt{5}}{4},\sin \frac{2\pi }{5}=\frac{\sqrt{10+2\sqrt{5}}}{4}$

For later use, we shall write down explicitly the values of ${\omega }^j$ for $1\le j\le 4$.

$\omega ={\text{e}}^{\frac{2\pi i}{5}}=\frac{-1+\sqrt{5}}{4}+\frac{\sqrt{10+2\sqrt{5}}}{4}i$

${\omega }^2=e^{\frac{4\pi i}{5}}=\frac{-1-\sqrt{5}}{4}+\frac{\sqrt{10-2\sqrt{5}}}{4}i$

${\omega }^3={\text{e}}^{\frac{6\pi i}{5}}=\frac{-1-\sqrt{5}}{4}-\frac{\sqrt{10-2\sqrt{5}}}{4}i$

${\omega }^4={\text{e}}^{\frac{8\pi i}{5}}=\frac{-1+\sqrt{5}}{4}-\frac{\sqrt{10+2\sqrt{5}}}{4}i$

Since $a\mathrm{,}b\mathrm{,}c\mathrm{,}d$ and e are roots of (4) we also have

$a+b+c+d+e=1$

Let $V_1\mathrm{,}{V}_2\mathrm{,}{V}_3$ and $V_4$ be defined as follows:

$\begin{array}{l}{V}_1=a+b\omega +d{\omega }^2+c{\omega }^3+e{\omega }^4\\ V_2=a+b{\omega }^2+d{\omega }^4+c\omega +e{\omega }^3\\ V_3=a+b{\omega }^3+d\omega +c{\omega }^4+e{\omega }^2\\ V_4=a+b{\omega }^4+d{\omega }^3+c{\omega }^2+e\omega \end{array}$

We note that $V_i$, for $1\le i\le 4$ lies in the field $\mathbb{K}=Q\left(\cos \frac{2\pi }{11}\mathrm{,}\omega \right)$ which is of degree 20 over $\mathbb{Q}$. It is easily seen that

$\begin{array}{l}a=\frac{1}{5}\left(1+V_1+V_2+V_3+V_4\right)\\ b=\frac{1}{5}\left(1+{\omega }^4{V}_1+{\omega }^3{V}_2+{\omega }^2{V}_3+\omega V_4\right)\\ c=\frac{1}{5}\left(1+{\omega }^3{V}_1+\omega V_2+{\omega }^4{V}_3+{\omega }^2{V}_4\right)\\ d=\frac{1}{5}\left(1+{\omega }^2{V}_1+{\omega }^4{V}_2+\omega V_3+{\omega }^3{V}_4\right)\\ e=\frac{1}{5}\left(1+\omega V_1+{\omega }^2{V}_2+{\omega }^3{V}_3+{\omega }^4{V}_4\right)\end{array}$

Since we already have radical expression for $\omega$, it is enough to give a radical expression for $V_i$ ’s for $1\le i\le 4$. This can be done by showing that the fifth powers of $V_i$ ’s lie in the field $\mathbb{Q}\left(\omega \right)$ and we shall have the radical expressions for the roots of (4) as soon as we have an explicit expression for the fifth powers of $V_i$ ’s as members of $\mathbb{Q}\left(\omega \right)$.

Consider the following diagram of the subfields of $\mathbb{K}=Q\left(\cos \frac{2\pi }{11}\mathrm{,}\omega \right)$

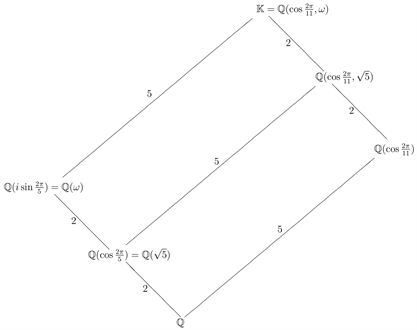
Evidently, the Galois group $G=Aut\left(\mathbb{K}/\mathbb{Q}\right)$ is cyclic of order 20. Let $\sigma$ denote the automorphism of the field $\mathbb{K}$ which fixes $\omega$ but cyclically permutes the five roots of (4) as follows:

$a\to b\to d\to c\to e\to a\mathrm{.}$

Let $\eta$ denote the automorphism of the field $\mathbb{K}$ which maps $\omega$ to ${\omega }^2$ (and so $\omega \to {\omega }^2\to {\omega }^4\to {\omega }^3\to \omega$ ) and fixes a (and therefore $b\mathrm{,}c\mathrm{,}d\mathrm{,}e$ ). Since $\sigma$ and $\eta$ commute and have orders 5 and 4 respectively, the automorphism $\sigma \eta$ has order 20 and we have

$G=Aut\left(\mathbb{K}/\mathbb{Q}\right)=\langle \sigma ,\eta \rangle =\langle \sigma \eta \rangle$

Table 1 below gives the effect of $\sigma$ and $\eta$ on $a\mathrm{,}b\mathrm{,}c\mathrm{,}d\mathrm{,}e$ and $\omega$ and Table 2 gives the Galois correspondence between the subfields of $\mathbb{K}$ and the subgroups of $G=Aut\left(\mathbb{K}/\mathbb{Q}\right)$.

Now as $V_1=a+b\omega +d{\omega }^2+c{\omega }^3+e{\omega }^4$, we have $\sigma \left(V_1\right)=b+d\omega +c{\omega }^2+e{\omega }^3+a{\omega }^4={\omega }^4\left(a+b\omega +d{\omega }^2+c{\omega }^3+e{\omega }^4\right)={\omega }^4{V}_1$

Therefore $\sigma \left(V_1^5\right)=V_1^5$ and so the fixed subfield of $\langle \sigma \rangle$ is $\mathbb{Q}\left(\omega \right)$. In other words $V_1^5\in \mathbb{Q}\left(\omega \right)$. Likewise $V_2^5\mathrm{,}{V}_3^5\mathrm{,}{V}_4^5\in \mathbb{Q}\left(\omega \right)$.

Table 1. Action of the Group $G=Aut\left(\mathbb{K}\right)$ on some generating elements of the field $\mathbb{K}$.

Table 2. Galois correspondence between the subgroups of $G=Aut\left(\mathbb{K}\right)$ and subfields of $\mathbb{K}$.

3. Conclusions

Although we know that $V_1^5\in \mathbb{Q}\left(\omega \right)$ but nevertheless, it is quite cumbersome to find an actual expression for it as an element of $\mathbb{Q}\left(\omega \right)$. It is hard to imagine how so very patiently Vandermonde may have carried out this computation. While doing calculation by hand it would be unwise to write down the $5^5=3125$ terms of $V_1^5={\left(a+b\omega +d{\omega }^2+c{\omega }^3+e{\omega }^4\right)}^5$ and then attempt to simplify these using the 15 relations from Vandermonde’s paper indicated earlier (and the fact that ${\omega }^5=1$ and $a+b+c+d+e=1$ ). The right approach would be to find the values of $V_1^2$, $V_1^3$, $V_1^4$ and $V_1^5$ in succession and simplifying each (i.e. expressing it as a linear polynomial in $a\mathrm{,}b\mathrm{,}c\mathrm{,}d$ and e with coefficients in $\mathbb{Q}\left(\omega \right)$ ) before attempting to find the next higher power. Undoubtedly, Vandermonde followed this approach although he neither so claims and nor does he give the expressions for $V_1^2$, $V_1^3$, $V_1^4$ and $V_1^5$ in his paper. The fact that Vandermonde’s end result is slightly incorrect does not in any way diminish our appreciation for his patiently carrying out enormous calculation by hand.

Since the automorphism $\eta$ of $\mathbb{K}$ permutes $V_i$ ’s cyclically as $V_1\to V_2\to V_4\to V_3\to V_1$, we only need to compute $V_1^5$. We shall not deprive the readers of the joy of calculating $V_1^5$ by hand. Here we shall content ourselves by giving the explicit expressions for $V_1^2$, $V_1^3$, $V_1^4$ and $V_1^5$. We have checked their correctness with the help of MATHEMATICA. For the purposes of calculations, we shall find it more convenient to write each power of $V_i$ as a polynomial in $\omega$ with coefficients which are linear in $a\mathrm{,}b\mathrm{,}c\mathrm{,}d$ and e.

$V_1=a+b\omega +d{\omega }^2+c{\omega }^3+e{\omega }^4$

$\begin{array}{c}{V}_1^2=\left(b-2d+2e\right)+\left(-2a+2d+e\right)\omega +\left(2a-2c+d\right){\omega }^2\\ +\left(a-2b+2c\right){\omega }^3+\left(2b+c-2e\right){\omega }^4\end{array}$

$\begin{array}{c}{V}_1^3=\left(2-8a-2b+2c-5d+4e\right)+\left(2+2a+4b-2c-8d-5e\right)\omega \\ +\left(2-2a-5b+4c+2d-8e\right){\omega }^2+\left(2+4a-8b-5c-2d+2e\right){\omega }^3\\ +\left(2-5a+2b-8c+4d-2e\right){\omega }^4\end{array}$

$\begin{array}{c}{V}_1^4=\left(-16+34a+28b+18c-7d+8e\right)\\ +\left(-16+28a-7b+8c+18d+34e\right)\omega \\ +\left(-16-7a+18b+34c+8d+28e\right){\omega }^2\\ +\left(-16+18a+8b+28c+34d-7e\right){\omega }^3\\ +\left(-16+8a+34b-7c+28d+18e\right){\omega }^4\end{array}$

$V_1^5=196+130\omega -255{\omega }^2+20{\omega }^3-90{\omega }^4$

In a like manner (or preferably by simply applying the automorphism $\eta$ ) we obtain similar expressions for $V_2^5\mathrm{,}{V}_3^5$ and $V_4^5$. These expressions are:

$V_2^5=196+20\omega +130{\omega }^2-90{\omega }^3-255{\omega }^4$

$V_3^5=196-255\omega -90{\omega }^2+130{\omega }^3+20{\omega }^4$

$V_4^5=196-90\omega +20{\omega }^2-255{\omega }^3+130{\omega }^4$

By substituting the values of ${\omega }^i$ for $1\le i\le 4$ in radical form we get the following radical expressions for $V_j^5$, for $1\le j\le 4$.

$V_1^5=\frac{11}{4}\left(89+25\sqrt{5}\right)+\frac{11}{4}\left(20\sqrt{10+2\sqrt{5}}-25\sqrt{10-2\sqrt{5}}\right)i$

$V_2^5=\frac{11}{4}\left(89-25\sqrt{5}\right)+\frac{11}{4}\left(25\sqrt{10+2\sqrt{5}}+20\sqrt{10-2\sqrt{5}}\right)i$

$V_3^5=\frac{11}{4}\left(89-25\sqrt{5}\right)-\frac{11}{4}\left(25\sqrt{10+2\sqrt{5}}+20\sqrt{10-2\sqrt{5}}\right)i$

$V_4^5=\frac{11}{4}\left(89+25\sqrt{5}\right)-\frac{11}{4}\left(20\sqrt{10+2\sqrt{5}}-25\sqrt{10-2\sqrt{5}}\right)i$

We observe that $V_1\cdot V_4=V_2\cdot V_3=11$. With appropriate choice of fifth roots of $V_1^5\mathrm{,}{V}_2^5\mathrm{,}{V}_3^5$ and $V_4^5$ we can find the radical expressions for the roots of the Equation (4). However to check the correctness of our expressions for $V_1^5\mathrm{,}{V}_2^5\mathrm{,}{V}_3^5$ and $V_4^5$ we proceed as follows.

Let ${\theta }_1$ and ${\theta }_2$ be defined as follows:

${\theta }_1=\arctan \left(\frac{20\sqrt{10+2\sqrt{5}}-25\sqrt{10-2\sqrt{5}}}{89+25\sqrt{5}}\right)\approx 6.8107268˚$

${\theta }_2=\arctan \left(\frac{25\sqrt{10+2\sqrt{5}}+20\sqrt{10-2\sqrt{5}}}{89-25\sqrt{5}}\right)\approx 76.890834˚$

then

$\begin{array}{l}a=-2\cos \frac{2\pi }{11}=\frac{1}{5}\left[1+2\sqrt{11}\left\{\cos \frac{{\theta }_1+6\pi }{5}+\cos \frac{{\theta }_2+6\pi }{5}\right\}\right]\approx -1.682507066\\ b=-2\cos \frac{4\pi }{11}=\frac{1}{5}\left[1+2\sqrt{11}\left\{\cos \frac{{\theta }_1+4\pi }{5}+\cos \frac{{\theta }_2+2\pi }{5}\right\}\right]\approx -0.830830026\\ c=-2\cos \frac{6\pi }{11}=\frac{1}{5}\left[1+2\sqrt{11}\left\{\cos \frac{{\theta }_1}{5}+\cos \frac{{\theta }_2+4\pi }{5}\right\}\right]\approx 0.284629677\\ d=-2\cos \frac{8\pi }{11}=\frac{1}{5}\left[1+2\sqrt{11}\left\{\cos \frac{{\theta }_1+2\pi }{5}+\cos \frac{{\theta }_2+8\pi }{5}\right\}\right]\approx 1.309721468\\ e=-2\cos \frac{10\pi }{11}=\frac{1}{5}\left[1+2\sqrt{11}\left\{\cos \frac{{\theta }_1+8\pi }{5}+\cos \frac{{\theta }_2}{5}\right\}\right]\approx 1.918985947\end{array}$

The correctness of these expressions can be easily checked with the help of a calculator. Finally, for the curious, we have the following explicit radical expression for $\cos \frac{2\pi }{11}$.

$\begin{array}{c}\cos \frac{2\pi }{11}=-\frac{1}{2}a=-\frac{1}{10}\left(1+V_1+V_2+V_3+V_4\right)\\ =-\frac{1}{10}[1+{\left\{\frac{11}{4}\left(89+25\sqrt{5}\right)+\frac{11}{4}\left(20\sqrt{10+2\sqrt{5}}-25\sqrt{10-2\sqrt{5}}\right)i\right\}}^{\frac{1}{5}}\end{array}$

$\begin{array}{c}+{\left\{\frac{11}{4}\left(89-25\sqrt{5}\right)+\frac{11}{4}\left(25\sqrt{10+2\sqrt{5}}+20\sqrt{10-2\sqrt{5}}\right)i\right\}}^{\frac{1}{5}}\\ +{\left\{\frac{11}{4}\left(89-25\sqrt{5}\right)-\frac{11}{4}\left(25\sqrt{10+2\sqrt{5}}+20\sqrt{10-2\sqrt{5}}\right)i\right\}}^{\frac{1}{5}}\\ +{\left\{\frac{11}{4}\left(89+25\sqrt{5}\right)-\frac{11}{4}\left(20\sqrt{10+2\sqrt{5}}-25\sqrt{10-2\sqrt{5}}\right)i\right\}}^{\frac{1}{5}}]\end{array}$

This indeed gives the correct value of $\cos \frac{2\pi }{11}$ with a proper choice of the fifth roots of unity in the above expression.

Acknowledgements

We would like to express our thanks and appreciation to two anonymous mathematicians for bringing to our attention references [3] [4] and [6]. We also thank Professor Clifford Johnston of the Department of Mathematics, West Chester University for his help with MATHEMATICA.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Vandermonde, A.T. (1771) Mémoire sur la résolution des équations, Histoire de l'Acad. Royale des Sciences (avec les mémoires de Math. & Phys. pour la même année, tirés des registres de cette Acad.), 365-416.
[2]	Tignol, J.-P. (2001) Galois’ Theory of Algebraic Equations. World Scientific, Singapore, 348 p. https://doi.org/10.1142/4628
[3]	Jones, P.S. (1976) Vandermonde, Alexandre-Théophile, Dictionary of Scientific Biography, Vol. 8, Charles Scribner’s Sons, New York, 571-572.
[4]	Neumann, O. (2007) Cyclotomy: From Euler through Vandermonde to Gauss. In: Bradley, R.E. and Sandifer, C.E., Eds., Leonhard Euler: Life, Work and Legacy, Elsevier, Amsterdam, 323-361. https://doi.org/10.1016/S0928-2017(07)80018-1
[5]	Hamburg, R.R. (1976) The Theory of Equations in the 18th Century: The Work of Joseph Lagrange. Archive for the History of Exact Sciences, 16, 17-36.
[6]	Lagrange, J. (1869) Oeuvres. Notes sur la théorie des équations, Note XIV (Où l’on donne la résolution générale des équations à deux termes), Gauthier-Villars, Paris, 354-355.