1. Introduction
In the light of the new idea of the “geometric structure” of particles [1] [2], here we are going to review one of the fundamental issues of modern cosmology: the Dark Matter (DM). As we know, the question of DM describes the presence of an invisible matter, which influences the stellar motions in various galaxies [3] [4] and galactic motions in the whole universe. In the last few years, the DM has also appeared increasingly responsible for galaxies’ origin and their grouping [5]. The various hypotheses and theories formulated about the DM have not solved the mystery, which envelops them. The epistemology teaches us that if a theory cannot solve the puzzles deriving from the phenomena described, then the base knowledge is insufficient. Thus, one needs to add other new pieces of knowledge because nothing is known about its nature. A reflection could help us: if the DM is almost 27% of all the massive energy (matter) of the universe and the visible Ordinary Matter (OM) is about 4%, then we might think the DM field-particle is an equally fundamental particle of the ones of OM, it is not marginal, see the “WIMP” [6]. Let us change perspectively from that used by the literature in investigating the DM: we will begin to say that the matter nature is unique, but with two different aspects: one of the OM, another of the DM. This reflection leads us to look for the DM particle among the “matter” already commonly known, which is “invisible” for a particular reason, instead of the OM. To understand this last aspect, we need to add knowledge to all that we know on the field theory. What new knowledge needs to be added to our issues? In previous publications [7] [8], we have already pointed out the new knowledge to add to the field theory. In this paper, we use this new idea: the particles are geometric structures of coupled quantum oscillators [7] [8] [9]. This geometric hypothesis, see Section 2.1, allows us to build the geometric forms of quarks and all hadrons, made of quarks. In Section 2.2, we show the golden geometric structures of charged pions and the component quarks’ mass values, see also the Section 2.3. In Section 2.4, we show that the structure hypothesis is based on a new operation of coupling of the quantum oscillators, and, thus, particles see the Ä-operation. Just the idea of the geometric structure allows us to investigate the nature of DM. An argumentation could help us. Recall the hadron phase in the evolutionary universe: the quarks begin to tie themselves to a certain universe evolution time, making the hadrons in this way. If we argue that the DM influences the galactic motions in the whole universe, as the OM in hadron form makes, then we could suppose that the DM nature is “hadronic” but no baryonic (see MACHO) [10]. We could so conjecture that a particular “hadronic” matter and DM are two different forms of the same species of the hadrons. Properly, see Section 3.1, we find that the DM is a different form of the structure of neutral pion, called “dark pion”, and other particles, like the proton and neutron. This last aspect is possible because of the geometric structure of these hadrons one can associate two different configurations of coupling of the IQuO components, where the IQuO is particular quantum oscillators [2] [11] [12] [13]. Therefore, when the hadronic phase had its debut together to the OM’s appearance, we have also had the DM one. Observing the dark pion structure, we can demonstrate that the dark pion cannot interact with charged leptons, and, like the neutral pion, cannot interact with weak particles. By using a particular mathematical procedure in this article, elaborated in previous works (see ref. [7] [8] ), we calculate the mass of the dark pion. Thanks to mass value (mdm = 133.89 MeV), in the lattice-universe theory framework [14], we can associate a lattice Udm to the DM, built on the particular value of mass, see the Section 3.2. In this framework, we calculate the number of DM particles (dark pions) and DM’s density in our universe, Section 3.3. Note that the DM would be mainly made up of dark pions and not baryons (nucleons); this is consistent with the literature on MD [10]. In Section 4.1, using the quark and nucleon’s geometric structure, we demonstrate the “not coupling” of dark pion with hadrons, without, however, denying local interactions (by the exchange of gluons) with quarks of hadrons. In this way, the DM is then indirectly visible, see ray gamma [15], which can be emitted by interactions between cosmic particles (cosmic ray) and particles (or “molecules”) of DM or its eventual annihilation. After, we demonstrate (Section 4.1) that the DM had origin with more frequency than the OM, by determining a much bigger DM density than the OM one. To the light of the news, we show, see Section 5.1, a possible experiment in which one could detect the dark pion.
2. The Structure Hypothesis of Particles
2.1. The Geometric Hypothesis
The conjecture of the geometric structure of particles was proposed in a series of articles [1] [2] [7] [8]. Its origin is in the “aureum” (golden) ratio between the Compton wavelength of Planck (
) and that of the proton (
):
(1)
Recall:
. The scale factor (10)19 can be due to the universe’s expansion, which keeps the relation between invariant physical quantities.
We also find a golden relation in the pentagon. Then, we conjectured a proton having a geometric structure, where the component quarks are coincident triangles (u, d, u), see Figure 1.
Specifically [9], quarks having a well-defined “Aurea Geometric Structure”. We referred to this aspect as Aureum Geometric Model (AGM) of quarks. The structure is not rigid: the two quarks (u, u) rotate around the side BC in a-configuration, and the two sides (BC, AB) in b-configuration, see Figure 2. Each vertex (A, B, C, D, E) is a quantum oscillator, coupled to others by quantum oscillators of junction (sides). Note the two geometric representations of the proton:
The a-configuration shows an electric charge equal to one, along the propagation side BC. The b-configuration does not admit an only propagation axis, and along the two sides (AB, BC) the electric charge is not an integer. The b-configuration points out an “unusual” proton, see later. Therefore, we think that an ordinary proton propagating along X-axis is in the a-configuration. In
![]()
Figure 1. The internal geometric structure of the proton.
![]()
Figure 2. The two Proton configurations.
(AGM), the particles cannot be punctual objects in Space-Time (see the Quantum Relativistic Theory of fields), but “golden” geometric forms of a not separable set of coupled quantum oscillators. This aspect represents a “new paradigm” in particle physics: all massive particles are geometric structures of coupled quantum oscillators(geometric hypothesis). Thanks to AGM, it is possible to explain fundamental issues [7] [8]: the origin of the mass of hadrons and quarks, the hadron spin, isospin, decay and other aspect fundamentals. To the geometric form of a particle, we associated a structure equation, by which we can calculate the masses of quarks, of mesons and nucleons [7] [8] [13]. So, the proton is a golden particle, and the three quarks (u, u, d) are golden triangles, where the side (BC), see Figure 2, are proportional to Compton wavelength assigned to the proton (
= h/mpc), thus [
=
= kp#
]. The (
) is the Compton wavelength of “free” quark, while (kp) is a coefficient of “elastic adaptation” when (u, d) quarks reciprocally bind for originating the proton. The same is for d-quark: [
= kp#
]. Just kp can be in relation with binding gluons of the (u, d) quarks; we point out [V(r)QCD ó kp], where V(r) is gluonic potential in QCD theory [16]; so in the AGM theory, the elastic tension k replaces the potential V(r) of the QCD. The ratio between the masses (both bare and bounded) of the two quarks is:
with (md > mu)
We notice that this structure can be realizable only through “particular” quantum oscillators, point out by the acronym (IQuO) [11] [12]. These quantum oscillators present a composite form with two sub-units of oscillation or “sub-oscillators”. The presence of more components in an oscillator causes the splitting of its quanta of energy in half-quanta placed into two, and more, sub-oscillators. The quarks (u, d) are so golden triangles of coupled IQuO.
2.2. The Geometric Structure of the Pion
When recalling the light mesons made of quark-antiquark pairs, in pion [2], the structure equation is:
. The elements (u, d) are matrices built by the representative operator of IQuO [2]. The Ä is a mixed operation [Ä = Ä, Å] with operations of coupling dynamics between quarks (Å) e of “interpenetration” (Ä) of quarks, see the ref. [2] [7] [8]. The Å-operation involve both gluons coupling and electromagnetic:
. The pion representation is, see Figure 3.
So, a quadrangular structure (ABDC) expresses a pion propagating along the X-axis. The bonds (gluons) between two free quarks (u ó d) increase the elastic tension between the IQuO components of quarks
: therefore, the “free” frequencies
and masses
increase. The π-structure is a similar system to two coupled oscillators (u ó d) which oscillate with frequency (ωπ), period (τπ) and (
, mπ). Each quark (u, d) contributes to total mass (mπ) with its mass value (mu, md), which keep the golden ratio [(md/mu) = f]. We can admit that in the (ki) the mass defects are contained (recall that k replaces the potential V(r)), so that we have
, and
. To the frequency ωπ, we associate kπ elastic coefficient, which is related to the gluonic potential V(r) of the QCD [16] and thus, in turn, is related to coupling (Å). Combining the two massive relations in pion, we have [1]:
(2)
where
is the charged pion mass (≈(139.57) MeV) The solution is:
(3)
with their gluons, the two quarks (uπ, dπ) are called dressed quarks. A system of two equations can give the bare masses of quarks (u, d), or [m(uf), m(df)], if we admit their masses in golden relation:
(4)
where
.
2.3. The Ä-Operation of Combination of Structures
Thanks to the AGM, it is possible to build the structures of mesons and “molecules of pions” [7]. The first evidence of success is the calculation of the mass
spectrum of light mesons (η, η', ρ, ω, f) and nucleons (n, p) with mass values which are very closed (if not even equal) to the experimental ones [17]. This calculation is possible thank to the introduction of the Ä-operation. The interpenetration operation (Ä) is an operation purely quantistic on the quarks, which involves the time beyond to be connected to spin. If the spin is associated with different configurations (orientations) in the space of the wave function of a particle, the interpenetration is associated with different configurations (orientations) in the time of a quark. We talk about a “quantum-relativistic” aspect in the Space-Time. The quark spin in the geometric model implies it rotates around the bond’s axis and propagation of the hadron. All spin configurations are admissible even those that admit interpenetrations of the two quarks. The same happens in the different configurations in time of a quark: we can also admit an interpenetration of it with itself, but considered at different times. These aspects can appear incredibly paradoxical, but instead, they allow us to calculate the masses of hadrons, see ref. [7] [8]. Therefore, the Ä-operation is the first example of a quantum-relativistic operation which allows us to treat the geometric structures from a quantum-relativistic standpoint.
3. The Dark Matter
3.1. The Dark Matter Particles
Recalling of the π± pion structure, that of a neutral pion is:
. The geometric representation is, see Figure 4.
Note two configurations in neutral pion: [(π0)a, (π0)b]. The first configuration ((π0)a) is the one that represents just the pion, observed in all hadronic interactions, The second configuration ((π0)b) expresses a possible physic state (see also the proton), which must have a phenomenologic manifestation in quantum mechanics (QM). We conjecture that could represent a particle of the DM (
). Note, Figure 4, that in ((π0)b) the (u, u) quarks are attached respectively to sides AD and BC, and they are also in rotation around the passing axis for AD (u-quark) and BC (u-quark) [2]. Even the (d, d) quarks are in rotation, but all quarks’ global spin is zero, like in the pion. We report the aspect of (π0)b in another time, now see Figure 5.
Note that the (X, Y, Z) axes are coplanar. Here the (π0)b is the particle of DM
![]()
Figure 4. Configurations of neutral pion.
or “dark pion” (π0)d. This configuration is stable, while that of ordinary pion is not, see its decay in two photons. In fact, in the pion (π0)a (see Figure 4) the two pair (d, d) and (u, u) cross along diagonal FH, where it is possible so annihilate in two photons. In (π0)d, the pair (d, d) cannot annihilate because the d-quark and d-quark have a “ballast” in the quarks (u, u), these last have no side in common and cannot annihilate. The (π0)d particle is electrically neutral, and it cannot act through photons. The two components charged pions cannot decay weakly, because the two d-quarks are hooked along the same diagonal AD. The weak decay in two muons is not possible due to mass issues too. However, the presence of two different decay axes (see Figure 5 the BD, AC) could be violated the conservation of momentum. If this no occurs, we could think of the double beta decay. Thus, weak non-decay excludes possible weak interactions with other quarks and leptons. Later, in this article, we will demonstrate that the dark pion cannot couple with other hadronic particles. However, instead, it can locally interact, with the exchange of gluons between quarks. It is clear that (π0)d can act gravitationally. As the proton also the neutron has two configurations, see Figure 6.
Note that the a-configuration shows an electric charge equal to zero along the propagation side AC. Even though the b-configuration is globally neutral, it shows an electric charge equal to −2/3, along the side AC. The b-configuration could be a dark neutron. Therefore, if the structure equation admits two possible configurations, then one of two is a dark particle. It follows that the DM particles do not allow couplings with hadrons, which transformation it. Besides, the DM has no interactions electromagnetic and weak, but it can interact gravitationally because it has mass. Nevertheless, we suppose that the DM can interact with other quarks by gluons exchange. Besides, note the Ordinary Matter (OM) has a function of determining the transformations and organization of physic systems to fulfil the universe evolution (phase transformations, galactic organization, star system formations, star energy production …). Instead, the DM has the function of keep aggregated the galactic matter to realize the transformations first said on the OM. To calculate the mass of (π0)d, we use the Fm-function, see eq. 20 in ref. [2]:
![]()
Figure 6. The two configurations of neutron.
(5)
where
, because u and u are not in interpenetration in (π0)d. Now, we calculate the mass defect. We turn to the matrix Aij (Table 1) of mass defects [7]:
The mass defect could be:
(6)
To calculate the mass defect of terms in red colour Ri, we need to consider the spin. About the (π0)d spin, we can have [8], see also the pion spin (π0):
(7)
Then, we will have:
(8)
![]()
Table 1. Table of the coupling with the interaction of quarks in a
.
Then R = 0. It follows:
(9)
The mass defect is:
(10)
Thus, it is:
(11)
In kg it is:
(12)
with a lower mass than the neutral pion. This aspect could lead us to think that the nucleons cannot exchange dark pions in their interactions, because they exchange ordinary pions and no particles with minor mass. We could have another possibility of the dark pion, see Figure 7.
We could so admit that the dark pion is degenerate into two configurations; nevertheless, we could also suppose that the structure of Figure 7 may represent another type of particle. We will see this in the next study. Now, the mass could be:
(13)
We get the same result as the previous case. The mass is still m = (133.89) MeV by having the same matrices of the mass defects.
3.2. The Dark Matter in the Universe
We recall, see ref. [14], the U-universe made up a set of “universe-lattices” Ui and by set of intersections between these Ui lattices (
).
![]()
Figure 7. Another configuration of the dark pion.
We write
. If we add the DM then we need to introduce the dark “universe-lattices” Ud. So, now, we define the Universe as
, here we have included the lattices of DM. All fields-particles with mass mi and space step
, the Compton wavelength, constitute the lattice Ui. The indirect presence of the not-radiative halos of matter (no optical photons), which envelope each galaxy, induces us to claim that the representation of dark matter can be the one of a universe lattice of dark mass (Ud). We can admit that there are intersections of (Ud) with other lattices Ui, you see the galactic halos of dark mass enveloping galaxies of “hydrogen” (UH) or the influence of dark matter on the movement of stars around the galactic centre. Note that the idea of intersection between two lattices implies an “intermediary” field, see the electromagnetic field (γ) which realize the universe lattice UH [14], the intersection between electron lattice Ue and that of the proton Up:
. The same it happens [14] in the Nucleosynthesis phase
where N is a nucleus, α is alpha-particle, π0 is the neutral pion, and q is an intermediary binding quark, see the same pion made of a quark-antiquark (q, q). Recall that the neutral pion is a base component of light mesons. Since the whole visible matter in the Universe is approximately baryonic matter (UB), we think that in a particular phase of the evolutionary universe there has been an intersection of (Ud) with lattices of baryonic matter (UB). This phase could be where the quarks have begun to tie to give origin to the mesons and baryons, recall the phase of hadronization. We point out this intersection lattice with UBd. In the current universe, to significantly influence the motion of stars, the dark matter must interact gravitationally in a way very intense, and this is possible only if it has high values of global mass. If we talk about dark pions, we may think that these can group in huge numerical amounts. This last aspect is possible if the dark pions can group in molecules and group of molecules. Thus, we might speculate that dark matter can aggregate into huge clusters of dark pion macromolecules (see Figure 11 later in the article). All this is possible thanks to the “geometric structure” of the dark pion, allowing couplings locals with quarks (by an exchange of gluons) of another dark pion. If the structure of a dark pion allows it to aggregate into molecules, we could have then that a hadron interacts with these agglomerates, and to produce a γ-radiation as also [15] [18] X-radiation, detected in astronomic observations) [19]. It is also possible that an only dark pion can interact with a nucleus (nucleons agglomerates) and so to produce a γ-radiation. Therefore, we can assume that the intersection-lattice
exists, where (B) is the baryonic matter (any baryonic particle or a group) which interacts with the dark particles. The UBd can be connected to the hadronic phase and the hydrogen phase, the universe’s current phase. In any relation between the two lattices [14], there must be some adaptation coefficient k,which adaptsthe different wavelengths of two lattices (Ui, Uj):
(14)
where (ks) is the adapting ratio, made by the number ratio between the two Compton wavelength at unless of a scale factor (10)s. We suppose that, in the current universe, the lattice
still exists. In this way, we can assume that [RBd= Rd = RH], where R is the universe’s ray described through the universe-lattice Ui. Then, the UBd, see ref. [14], will be:
(15)
where nd is the step number (the step is
) of DM lattice in UBd and Ud. Let us we consider the nucleons (B ó p, n) as baryonic matter. We will have the (
è
) as a ray of baryonic interaction (only elastic collisions) between a nucleus and the DM. The parameter (η) concerns the interaction between the dark pion and hadron molecules or vice versa. Since the number particles N, into lattice Uk, is given by [N = n2], where (n) is the number step (
), then ηd will be [ηd = (n)1/2g] where g is the intensity of gluon interaction (g = 1). In contrast, n is the number of quarks of one hadron molecule or a dark pion molecule, see the structures of nucleons and dark pion. So, the step number (n) is:
(16)
Nevertheless, see the ref. [14], the number of particles [N = n2]:
(17)
where NBd is the number of dark particles of Ud, which can collide elastically with UB baryonic.
3.3. The Density of Dark Matter
After we have found the mass of the DM particle, now we could calculate the dark matter density in the universe. We know the DM particle, with mass value m(πd) = (133.89) MeV/c2. In kg it is:
(18)
Its Compton wavelength is:
(19)
Now, we determine the value of adaptation coefficients k. In UBd it is:
(20)
where φ is the golden ratio. The number of dark particles is:
(21)
The density will be:
(22)
The cosmologic parameter Ω of metrics’ ratio is, see the critic density ρc:
(23)
The parameter η is related to the number n of quarks in a a molecule of dark pions, η = n1/2. In a molecule, see Figure 11, there are (n = 30) or (n = 28); it follows:
(24)
If the molecule number is (28), we have [ρd ≈ (29)%(ρc)].
4. The DM Particles and Their Interaction
A New Description of the Reaction (p + π0)
In AGM, we show the interaction between a proton and a pion:
. Where p* is a transition excited state. The terms (u, d) in the structure equation of the pion and proton are matrices in the representation of the operators (a, a+) projected in the space of the IQuO oscillators [2]. The operation Ä combines the quarks following some indications given by structure. The graphic representation is, see Figure 8.
This reaction has a mathematics representation by matrices with the operators (u, d):
(25)
Note the identity-operator, used for coupling the operators of two matrices, because one needs to transform the first matrix (1 × 3) in (1 × 4). In the geometric representation, the placing order of operators follows the configuration of the particle structure. The product between two matrices implies the product between terms on line (a1Äb1), (a2Äb2), (a3Äb3), (a4Äb4). There are four possible places of I-operator, which give us four possible reactions. The first is:
(26)
That is:
. There are three different positions of (I)
![]()
Figure 8. Interaction between the proton and pion.
which give two photons to end of the reaction. Instead, the last of the four reactions is:
(27)
That is
. Note the proton and pion overlap and exchange quanta and quarks along the propagation X. We prove if the reaction (p + (π0)d) is possible. The graphic representation is, see Figure 9.
The axes (X, Y, Z) are coplanar. By the matrices, we have:
(28)
Any reaction:
. Another configuration with a different place of the I-operator gives the same result. The dark pion does not directly couple with the proton, the same with other baryons. Note that the proton overlaps the dark pion only along the X-axis side, where there can be some exchange of quanta (semi-quanta) but no quarks. The same happens with ordinary pions and mesons, as in the proton, because the two quarks (u, u)d of the dark pion are attached to different axes from X-axis. Therefore, we admit that the (π0)d can locally interact (along a side) with a hadron, but cannot directly couple
![]()
Figure 9. Interaction between the proton and dark pion.
with it or transform themselves in another particle. Nevertheless, if a lattice
there is present, then it is possible that the quarks [(uπ)Z, (uπ)Y] by the lattice can interact and couple with others quarks. Then, we obtain:
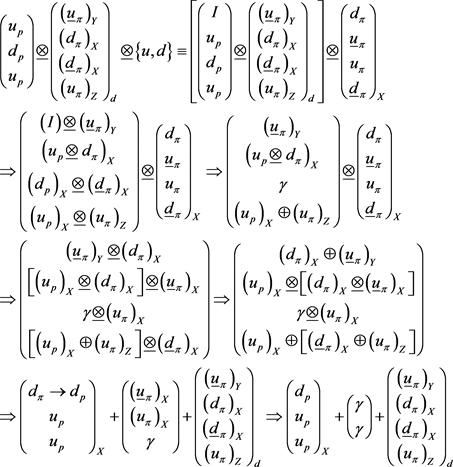 (29)
(29)
Note that the transition (
) occurs because the quarks (up)X, (uπ)Z, do not have sides in common except for a vertex, where they can exchange some quanta.
Note that
, where (π0)v is virtual neutral pion. So, the possible reaction is:
Where (π0*)d and (π0*)v are in an excited state, with full semi-quanta, see the IQuO [11] [12]. So, we can admit that if a proton passes through a group of excited dark pion molecules, the emission of γ-ray is possible. Recall two recent articles [20] [21] which some observations of galactic γ-ray report, apart from the already mentioned series of articles on cosmic γ-ray detections. An elucidation: the DM is only hadronic but non-baryonic. The leptons and quarks have an elementary unique geometric structure, while the hadrons are composites. The DM is one of two forms geometric of some hadrons, see the proton, the neutron and pion. If we demonstrate that
, then we show that OM ó DM or the matter can originate the dark matter and vice versa. Nevertheless, we can show that the transformation DM è OM is very unlikely, because in (π0)d. the two quarks (u,u) are in different axes. Now, we show, see Figure 10(a) and Figure 10(b), the reaction of dark pion production:
.
![]() (a)
(a)![]() (b)
(b)
Figure 10. (a) Coupling between two charged pions by of virtual neutral pion originating two dark pions; (b) Molecules of two dark pions after coupling
.
By the matrices, we have:
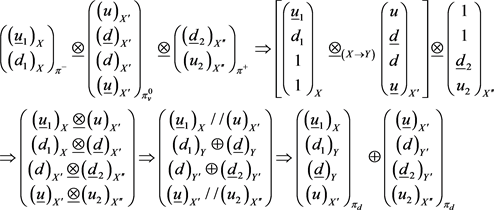 (30)
(30)
The reaction is:
Note a negative pion π− comes upon the lattice {
}; the (
) stops the rotation of d1-quark by the gluons of the d-quark. If the new molecule of quark comes upon a positive pion, it happens the fixing again and a molecule of two dark pions originates. Note that in the molecule
there is a virtual neutral pion
. We observe that the molecules
can be considered as
propagate along the axis X', see the Figure 10(b). So, if a neutral pion π0 couples with
and annihilates (
), a dark pion (
) remains. Therefore, the inverse reactions can be:
Note that the two dark pions can tie with others dark pions and giving origin to group molecules of dark pions, see Figure 11.
Note that a lattice of dark pions can trap an ordinary pion. In this case, the ordinary pion could not decay. It is possible that a proton propagating along an axis, could meet a trapping pion inside a lattice of dark pions, and, thus, it could accelerate. We can find this phenomenon in the cosmic ray, where the proton can accelerate because of galactic halos. Finally, we could say that the DM has to take origin from the annihilation process of matter-antimatter. However, this annihilation process does not lead to pure energy but to neutral matter which can originate gravitation. Thus, the DM present in the whole universe contains a remarked amount of annihilation energy matter-antimatter. The following representative diagram, see Figure 12, proves a surplus of DM during the transformations of energy ó matter-antimatter of the universe evolution (see phase GUT where q ó lepton).
The surplus of DM is determined by the origin of leptonic matter, which can never to originate the DM. The pions originate photons which in turn create other pairs [(q, q), (l, l)]: the pairs of leptons can never originate DM, instead,
the pairs (q, q) can originate DM. In the late of this process, there is a surplus of DM.
5. An Experiment to Detect the Particle of Dark Matter
General Notes
The experiment proposed by us consists of studying the scattering of a beam antiprotons’ which hits a target and can produce dark particles. The representation of the reaction could be, see Figure 13.
To first order one has:
(31)
The reaction is:
If the energy of the antiproton increases, the reaction involves the lattice {
}. To second order we will have:
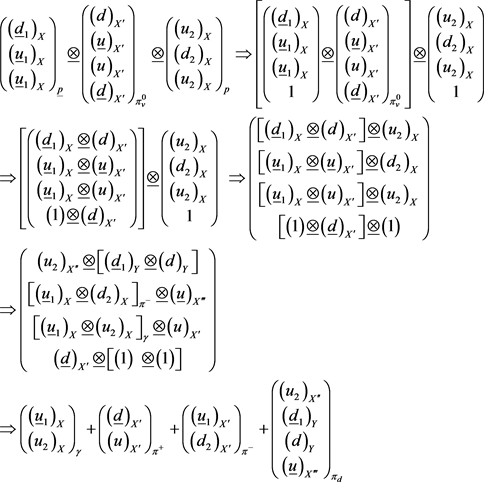 (32)
(32)
Then, the reaction is:
.
Note the presence of lattice [(u, u), (d, d)] which allows the reaction of production of a dark pion with γ-ray. The dark pion emerges with an angle of 36˚ along the axis Y, coplanar to X-axis, see Figure 13. We then have to carry out an experiment in which a thin beam of antiprotons hits a target, with the energy
![]()
Figure 13. Production of dark pion from annihilation (p + p) in the target with a nucleon p.
needed to produce a pion pair, a gamma photon and a dark pion, with an exit angle of 36˚. Current technology and statistical data processing can allow us to perform such an experiment. The production of a dark pion is an event at low probability, and, thus, with a small collision cross-section. Therefore, we have to set up an experiment that can reveal sporadic events and highlight them statistically. The DM detector will be a hadronic calorimeter capable of measuring low energies, (particles with energy at rest of 134 MeV). Our goal is to detect only dark pions. Therefore, only the dark pion must enter the calorimeter and nothing else. We must then provide the calorimeter with a shielding suitable to prevent particles such as pions, muons, and gamma rays from passing, see Figure 14. As we know the extreme difficulty of detecting Dark Matter, we considered several important theoretical and practical problems. At the nuclear distance of about 10−15 meters, the gravitational interaction is of the order of 10−39 N, a quantity that is difficult to measure. So, we have to rely on the little intense “strong” interaction of dark pion with the nuclei present in the hadronic calorimeter (gluon exchange between the respective structures). It was therefore thought of a way to detect DPs, by assimilating them to neutrons slowed down by paraffin. Therefore, paraffin sheets could be used with a thickness such as to absorb neutral particles except for the dark pion which would be slowed down to passing. An additional shield (lead plate) could absorb the gamma rays produced in our reaction. The muons (produced by the charged pions’ decay) could be deflected by a magnetic field, where the paraffin is immersed. In the paraffin, the dark pions interact very mildly like a glass marble that penetrates a compact agglomeration of glass marbles. In the case of the DP, we can thus associate a series of elastic collisions between quarks (gluon agents). In this way, the dynamics of the collisions are Newton’s. As we know the masses involved are 130 MeV for the dark pion and 938 MeV for the nucleons of Carbon and Hydrogen, contained in the paraffin. Not knowing the speed of the dark pion, the relative variation of its kinetic energy in every single elastic collision can be:
(33)
where v and v' are the dark pion’s speeds before and after the collision;
is the initial kinetic energy and
is the final kinetic energy (after the collision). In the reference system at rest of the nucleon, with M as mass, is:
Therefore, we obtain:
(34)
while for π0 the factor is: 0.4520155. Note ΔEr coincides with the neutron slowdown factor Fr. Nevertheless, if we consider the initial speed of
is 99.975% of c, the number of collisions that lead to the absorption of the particle is 65. This value is obtained by applying the following equations:
From which the non-relativistic speed v' can be derived after each impact
(35)
The dark pion enters the paraffin at a certain angle of 36˚ and since the cross-section is very small, it will always go out at an angle of approximately 36˚, see Figure 14. We suspect that the dark pions enter the calorimeter with this angular value and with an energy of about 18 MeV: if the calorimeter detects a signal, it is likely that it is the dark pion. To deflect any muon, we use deflector magnets (about 300 Tesla). The experimental apparatus could be, see Figure 14.
The cross-section of the calorimeter is, see Figure 15.
Where: yellow (refined paraffin), black (X-ray sensitive plate), red (hadronic calorimeter), green (dipole magnets), purple (iron layer covered with radiation resistant plastic materials).
Note that the instrumentation and experiment described in this section are purely indicative and by no means represent an operational proposal with all the
![]()
Figure 15. A cross section of the calorimeter.
details required to achieve the executive precision and the established research objectives.
6. Conclusions
In this paper, we have seen that the structure hypothesis is a new idea, which could complete our vision of matter. Thanks to the idea of structure, we see that it is possible to associate two equivalent forms to a geometric structure of a base particle of matter. If the first configuration is associated with a common particle (as pion), see Figure 4, the second configuration needs to be associated with a no common pion, “hardly” observable or “dark”. The same is for the proton, neutron and other hadronic particles. So, the matter present in the universe can have two forms: the first, with low density (about 5%), is indicated as Ordinary Matter (OM), while the second, with greater density (in this paper placed approximately between 27% and 29%), is the Dark Matter (DM). In DM, the dark particle more abundant is the pion because this can group in molecules and macromolecules. The DP allows us to talk about the DM as a no-baryonic matter, according to literature, but, with many surprises, of hadronic nature (pion). If our idea is correct, then DM particles’ current creation is always associated with gamma-ray emission, see the Section 4.1. Note the astronomic observations of galactic halos have highlighted this phenomenon of γ-emission. The gamma-ray emission can also exist when a “cosmic” particle collides with DM of halos, see Equation (29). Nevertheless, the literature states that the gamma emission is purely a consequence of annihilation processes of DM (or self-destruction [15] ). We believe that these processes are at low probability, a consequence of the particular structure of dark pion, see the possible violation of impulse conservation. Nevertheless, we could suppose an annihilation process of DM only in presence of an excited physical state of the lattice (
), see Equation (29). In this case, we could have the following reaction:
This is the inverse reaction of production of the dark pions, see Equation (30). Nevertheless, our attention has focused on DM production reaction. Then, we analyzed the possibility that an antiproton, hitting a target, could produce a dark pion. About this reaction, it is possible to realize an experiment with appropriate instrumentation, see Section 5. We believe that this experiment can be doable, and it can give us the possibility to verify our hypothesis of structure and to unravel, at last, the nature of DM. A note is due. Defining the DM nature allows us to shed new light on cosmological issues and the nature of gravitation. In the cosmological GR, the mass-energy tensor T should include any form of matter and energy, which contribute to the universe’s curvature, including the DM. Instead, the cosmological coefficient Λ, relative to the universe acceleration, can be placed either on the first member of Einstein’s equation [R + Λ = κT], see the bibliography [22], and on the second member [R = κT+ Λ]. The first case Λ expresses a property of the S-T [22]. In contrast, in the second member, it would express an additional property of the universe’s energy, see the dark energy [23]. An excellent synthesis of the various theories on this cosmological problematic can be found in the expletive and exhaustive essay by Corda [23], where he notes that the study of gravitational waves could exclude some approaches to GR, see the extended GR. The hypothesis of a “pionic” nature of the Dark Matter and the particular structure of the dark particle makes us understand why the DM can aggregate into huge clusters (galactic halos) that have contributed to galaxies’ formation and their durability over time.