Combined Optimal Stopping and Mixed Regular-Singular Control of Jump Diffusions

Charles Kusaya¹, Memory Mandiudza², Nicholas Mwareya², Confess Matete², Leonard Shambira², Nyashadzashe Ngaza²

¹Department of Applied Mathematics; National University of Science and Technology, Bulawayo, Zimbabwe.
²Department of Mathematics and Computer Science, Great Zimbabwe University, Masvingo, Zimbabwe.

DOI: 10.4236/jmf.2021.112010                

Abstract

In this paper, we examine a model that maximises dividend payments for an insurance company with a debt liability. We assume that the company has a policy to reinvest a proportion of its surplus cash before paying dividends to shareholders. We model the dynamics of the cash reserves as a jump-diffusion process. Combined optimal stopping and mixed regular-singular control of the jump-diffusion process is presented and investigated. In the paper, we show that when the premium rate  is less than the liability rate , then the company should not get into business and the optimal dividend policy is to immediately pay out the initial cash reserve as dividends to shareholders. For the case , we show that the optimal risk management depends on the current level of the cash reserves. We demonstrate that the company’s optimal dividend policy is to pay out as dividends surplus cash above a predetermined threshold. We also present numerical examples to illustrate the results obtained.

Keywords

Jump-Diffusion, Brownian Motion, Solvency Region, Optimal Stopping Time, Mixed Regular-Singular Control, Reinsurance

1. Introduction

Dividend decisions are mainly concerned with financial policies on the payment of cash dividends to shareholders in the present or at a latter date. The decision to issue dividends depends on the firm’s excess cash reserve or profit and its envisaged long term earning capacity. Management is expected to pay out some or all of the cash surplus as dividends if it is not required by the firm. In some instances, excess cash is retained to support future organic growth of the company.

In recent years, several researchers have studied extensively dividend optimisation problems [1] - [10]. This has resulted in various strategies and mathematical models being developed using stochastic control theory [8]. The common dividend payment strategies in literature are band, barrier, threshold and impulse. Scheer, [8] defines the band strategy as one that involves partitioning of state space of the cash reserve in three adjunct sets, A, B and C. Dividends are paid according to the set where the level of cash reserves at time t, and $X\left(t\right)$ is located. For example, if $X\left(t\right)$ is in A, then the income premium is paid as dividend. The barrier strategy is a special case of the band strategy where the set A consists of only one point, say $x^{\mathrm{<mo>\; *\; </mo>}}\ge 0$ and dividends are only paid to shareholders when the amount of cash reserves exceed this point.

Taksar and Zhou [9], examine a dividend optimisation problem of an insurance company with a corporate debt liability such as a coupon bond or amortisation loan. A mixed regular-singular control problem is presented and investigated. The objective is to find a policy that maximises the expected total discounted dividend payout until the time of bankruptcy. In the model, the dynamics of the corporate assets is modelled as a diffusion process with the drift and diffusion coefficients being affine functions of the risk control variable. Taksar and Zhou show that the optimal dividend pay-out policy is to keep the total reserve below a certain optimal level $b_1$ , distributing the excess as cash as dividends. On the other hand, the qualitative behaviour of the optimal risk management depends on the ratio between the profit $\mu$ and the liability rate $\delta$ . When $\mu \le 2\delta$ , then it is optimal not to have reinsurance at all, namely, to take the full risk. On the other hand, if $\mu >2\delta$ , then the optimal risk management depends on the current amount of the reserve. There exists $b_0<b_1$ such that the optimal risk $a\left(x\right)$ as a function of the reserve x is a strictly increasing function on $\left[\mathrm{0,}{b}_0\right]$ , and $a\left(x\right)=1$ for all $x>b_0$ .

Zou, etal. [10] present a dividend optimisation problem (for an insurer) with a jump-diffusion risk process in the presence of fixed and proportional transaction costs. Due to the presence of transaction costs, an impulse stochastic control problem is formulated. The stochastic control problem is transformed into a quasi-variational inequality for a second-order non-linear integro-differential equation. Further, the problem is solved under the risk-neutral assumption for the insurer and the value function together with the optimal policy is constructed.

He and Liang [3] investigate optimal financing and dividend control of an insurance company with a proportional insurance policy. The problem is formulated as a mixed singular-regular control problem and solved using dynamic programming. The underlying cash reserve dynamics is modelled using linear Brownian motion [3] considering an optimal dividend and reinsurance strategy of a property insurance company under catastrophe risk.

Empirical studies, however, have shown that the jump-diffusion process reflects better changes that can occur in the level of the liquid assets of an insurance company due to unusual events such as earthquakes and floods [3] [11]. Rare events usually result in huge claims which reduce significantly the amount of cash reserves available to the company. Abrupt changes in the level of the available liquid assets due to unusual events will appear as discontinuities in the cash reserve trajectory. In this study, we extend the problem investigated by Taksar and Zhou [9] by modelling the dynamics of the cash reserve process using a jump-diffusion process. Taskar and Zhou [9] consider a model to maximize the expected total discounted dividend pay-outs for a company with debt liability. In this model, the corporate assets follow diffusion process with diffusion and drift coefficients being affine functions of the risk control variable. Further, we assume that the company has a policy to reinvest a proportion of its excess cash before paying dividends to shareholders. This kind of model is important especially in the context of property insurance. It is important to highlight that only negative jumps are considered in the model under study. The company’s management is faced with a situation where they need to find an optimal business policy that maximises the expected total discounted pay-out. Each business policy is associated with different levels of risk and expected profits. The most basic risk to the company under consideration emanates from claims made by clients on account of the fact that claim sizes vary and their occurrence times are random. This kind of risk is mitigated in the model through reinsurance.

In this paper, we also make the assumption that the company needs positive reserves in order to operate and the company is considered bankrupt as soon as the available cash reserves become negative. Accordingly, we define the bankruptcy time $\tau$ by

$\tau =\inf \left\{t\ge 0:X\left(t\right)<0\right\}.$ (1.1)

This problem under investigation is unique since it is the first time when a combined optimal stopping and mixed regular-singular control problem involving debt and reinvestment is solved assuming that the dynamics of the underlying cash reserve process is modelled by a jump-diffusion process. In this paper, the researcher chose combined optimal stopping and mixed regular-singular control since it adequately addresses the insurance problem of dividend maximisation and risk minimisation.

The structure of the paper is organised as follows: In Section 2, we present a rigorous mathematical formulation of the general problem on combined optimal stopping and mixed regular-singular control of jump diffusions. Section 3 deals with the application of the general mathematical problem presented in Section 2 to insurance. Section 4 is devoted to a detailed analysis and complete solution of the problem considering different cases of key parameter values such as $\mu <\delta$ and $\mu \ge \delta$ . In Section 5, we present the numerical examples to illustrate the results obtained in Section 4.

2. Problem Formulation

Consider four components that affect changes in the level of the cash reserves of an insurance company and these are premiums, debt repayments, claims and dividend pay-outs. The first two components namely, premiums and debt repayments are assumed to be deterministic and occur at a constant rate. Dividend payments are determined by the amount of cash reserves available at any given time. Claim sizes vary and occur at random times. A jump-diffusion process is considered in modelling the dynamics of the liquid assets since rare events such as earthquakes and floods can result in huge claims that reduce significantly the amount of liquid assets available to the company. We also take into account the need for the company to mitigate risk arising from its core business through reinsurance. Reinsurance means controlling revenues by diverting a proportion $1-a$ of all premiums to another company, in which case $1-a$ fraction of each claim is paid by the other company (Taksar and Zhou, 1998). Suppose $X\left(t\right)=X\left(t,\omega \right)\in \left[0,\infty \right]\times \Omega$ be a stochastic process on a filtered probability space $\left(\Omega \mathrm{,}\mathcal{F}\mathrm{,}{\mathcal{F}}_t\mathrm{,}P\right)$ representing the amount of liquid assets at time t. In this section we begin by considering the general problem formulation on mixed regular-singular control presented by [1] [7]. Let $\kappa =\left[{\kappa }_{ij}\right]\mathrm{<mo>\; :\; </mo>}ℝ\to {ℝ}^{k\times p}$ and $\theta =\left[{\theta }_i\right]\mathrm{<mo>\; :\; </mo>}{ℝ}^k\to {ℝ}^p$ be given continuous functions. Assume the the dynamics of the state $X\left(t\right)=X^{\left(\alpha \mathrm{,}\zeta \right)}\left(t\right)\in {ℝ}^k$ is described by the following equation:

$\begin{array}{c}\text{d}X\left(t\right)=b\left(X\left(t\right),\alpha \left(t\right)\right)\text{d}t+\sigma \left(X\left(t\right),\alpha \left(t\right)\right)\text{d}B\left(t\right)\\ +{\displaystyle {\int }_{{ℝ}^l}}\gamma \left(X\left(t^{-}\right),\alpha \left(t^{-}\right),z\right)\tilde{N}\left(\text{d}t,\text{d}z\right)+\kappa \left(X\left(t^{-}\right)\right)\text{d}\zeta (\; t\; )\end{array}$

and

$X\left(0^{-}\right)=y\in {ℝ}^k\mathrm{.}$

$\zeta$ is our singular control since $\text{d}\zeta \left(t\right)$ may be singular with respect to the Lebesgue measure $\text{d}t$ . The process $\zeta \left(t\right)\in {ℝ}^p$ is non-negative, right continuous and ${\mathcal{F}}_t$ adapted. Assume also that the performance function is given as follows;

$\begin{array}{c}{J}^{\left(\tau \mathrm{,}\alpha \mathrm{,}\zeta \right)}\left(x\right)=E^x[{\displaystyle {\int }_0^{{\tau }_s}}f\left(X\left(t\right)\mathrm{,}\alpha \left(t\right)\right)\text{d}t+g\left(X\left({\tau }_s\right)\right)\cdot {\chi }_{{\tau }_s<\infty }^2\\ +{\displaystyle {\int }_0^{{\tau }_s}}{\theta }^{\text{T}}\left(X\left(t^{-}\right)\right)\text{d}\zeta \left(t\right)]\end{array}$

where $g\mathrm{<mo>\; :\; </mo>}{ℝ}^k\to ℝ$ and $\theta \mathrm{<mo>\; :\; </mo>}{ℝ}^k\to {ℝ}^p$ are given continuous functions, ${\tau }_s=\inf \left\{t>0:X^{\left(\alpha ,\zeta \right)}\left(t\right)\notin S\right\}$ . Let also ${\tau }_m^{\mathrm{<mo>\; *\; </mo>}}$ for $m=1,2,\cdots$ be the time of bankruptcy, that is, ${\tau }_m=\inf \left\{t>0:X\left(t\right)\le 0\right\}$ . Let $\mathcal{A}$ be the set of admissible controls $\left(\alpha \mathrm{,}\zeta \right)$ such that the general equation above has a strong and unique solution. Further, suppose the following condition is satisfied:

$E^y\left[{\displaystyle {\int }_0^{{\tau }_s}}\left|f\left(X\left(t\right),\alpha \left(t\right)\right)\right|\text{d}t+\left|g\left(X\left({\tau }_s\right)\right)\right|\cdot {\chi }_{{\tau }_s<\infty }^2+{\displaystyle {\int }_0^{{\tau }_s}}{\displaystyle \underset{j=1}{\overset{p}{\sum }}}\left|{\theta }_j\left(X\left(t^{-}\right)\right)\right|\text{d}{\zeta }_j\left(t\right)\right]<\infty .$

where $E^y$ is expectation with respect to the probability law P given that $X\left(0^{-}\right)=y$ . The problem is to find the value function $\varphi \left(y\right)$ , the optimal mixed control $\left({\alpha }^{\mathrm{<mo>\; *\; </mo>}}\left(t\right)\mathrm{,}{\zeta }^{\mathrm{<mo>\; *\; </mo>}}\left(t\right)\right)\in \mathcal{A}$ and the optimal stopping time ${\tau }^{\mathrm{<mo>\; *\; </mo>}}$ such that;

$\varphi \left(x\right)=\underset{\left(\tau ,\alpha ,\zeta \right)\in \mathcal{A}}{\sup }{J}^{\left(\tau ,\alpha ,\zeta \right)}\left(x\right)=J^{\left({\tau }^{*},{\alpha }^{*},{\zeta }^{*}\right)}\left(x\right)$ (2.1)

Theorem 2.1. (Integro-variational inequalities for Combined Optimal Stopping and Mixed Regular-Singular Control of Jump-diffusions)

(a) Suppose there exists a function $\varphi \in C^2\left(S^o\right)\cap C\left(\bar{S}\right)$ such that:

(i) $\mathcal{L}\varphi \left(t\mathrm{,}x\right)+f\left(t\mathrm{,}x\right)\le 0$ for all controls $\left(\alpha \mathrm{,}\zeta \right)\in \mathcal{A}$ and $\left(t\mathrm{,}x\right)\in S$ .

(ii). ${\displaystyle {\sum }_{i=1}^k}{\kappa }_{ij}\left(x\right)\frac{\partial \varphi }{\partial x_i}+{\theta }_j\left(x\right)\le 0$ for all $\left(t\mathrm{,}x\right)\in S$ , $j=1,2,\cdots ,p$ .

(iii). $\begin{array}{l}{E}^y[{\displaystyle {\int }_0^{{\tau }_s}}\{{\left|{\sigma }^{\text{T}}\left(X\left(t\right),\alpha \left(t\right)\right)\nabla \varphi \left(t,X\left(t\right)\right)\right|}^2\\ +{\displaystyle {\sum }_{k=1}^l}{\displaystyle {\int }_R}{\left|\varphi \left(X\left(t\right)\right)+{\gamma }^k\left(X\left(t\right),\alpha \left(t\right),z\right)-\varphi \left(t,X\left(t\right)\right)\right|}^2{v}_k\left(\text{d}z\right)\}\text{d}t]<\infty \end{array}$ for all $\left(\alpha \mathrm{,}\zeta \right)\in \mathcal{A}$ .

(iv). $X\left({\tau }_s\right)\in \partial S$ almost surely on $\left\{{\tau }_s<\infty \right\}$ and ${\lim }_{t\to {\tau }^s}\varphi \left(X\left(t\right)\right)=g\left(X\left({\tau }_s\right)\right)\cdot {\chi }_{{\tau }_s<\infty }^2$ , ${\tau }_m^{*}=\inf \left\{t\ge 0:X\left(t\right)\le 0\right\}$ .

(v). ${\left\{{\varphi }^{-}\left(t\mathrm{,}X\left(t\right)\right)\right\}}_{t\le {\tau }_s}$ is uniformly integrable for all $\left(\alpha \mathrm{,}\zeta \right)\in \mathcal{A}\mathrm{,}\left(t\mathrm{,}x\right)\in \mathcal{S}$ and $\varphi \left(t\mathrm{,}x\right)\ge \Phi \left(t\mathrm{,}x\right)$ for all $\left(t\mathrm{,}x\right)\in \mathcal{S}$ .

(vi). Define the non-intervention region D by; $D=\left\{\left(t,x\right)\in \mathcal{S}:{\max }_{i<j<p}{\displaystyle {\sum }_{i=1}^k}{\kappa }_{ij}\frac{\partial \varphi }{\partial y_i}+{\theta }_j\left(y\right)<0\right\}$ and suppose $E^y\left[{\displaystyle {\int }_0^{{\tau }_s}}{\chi }_{\partial D}\left(X\left(t\right)\right)\text{d}t\right]=0$ .

Further, assume that for all $\left(t\mathrm{,}x\right)\in \bar{D}$ , there exists a mixed control ${\pi }^{\mathrm{<mo>\; *\; </mo>}}=\left({\alpha }^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}{\zeta }^{\mathrm{<mo>\; *\; </mo>}}\right)\in \mathcal{A}$ such that $\left(t\mathrm{,}{X}^{{\pi }^{\mathrm{<mo>\; *\; </mo>}}}\right)\in \bar{D}$ for $t>0$

(vii) $\mathcal{L}\varphi \left(t,x\right)+f\left(t,x\right)=0$ .

(viii) ${\displaystyle {\sum }_{k=1}^p}\left\{{\displaystyle {\sum }_{i=1}^k}{\kappa }_{ij}\left(X\left(t^{-}\right)\right)\frac{\partial \varphi }{\partial y_i}\left(X\left(t^{-}\right)\right)+{\varphi }_j\left(X\left(t^{-}\right)\right)\right\}\text{d}\zeta {\left(t\right)}^c$ for all t, $t\le j\le p$ where ${\zeta }^c\left(t\right)$ is the continuous part of $\zeta \left(t\right)$ .

(ix) ${\Delta }_{{\zeta }^{*}}\varphi \left(t_n,X\left(t_n\right)\right)+{\displaystyle {\sum }_{j=1}^p}{\theta }_j\left(X\left(t_n^{-}\right)\right)\Delta {\zeta }_j^{*}\left(t_n\right)=0$ for all jumping times $t_n$ of ${\zeta }^{\mathrm{<mo>\; *\; </mo>}}\left(t\right)$ and

(x) ${\lim }_{R\to \infty }{E}^y\left[\varphi \left(X^{{\pi }^{*}}\left(T_R\right)\right)\right]=E^y\left[g\left(X^{\left({\alpha }^{*},{\zeta }^{*}\right)}\left({\tau }_s\right)\right)\cdot {\chi }_{{\tau }_s}<\infty \right]$ , where $T_R=\min \left({\tau }_s,R\right)$ for $R<\infty$ . Then $\varphi \left(y\right)=\Phi \left(y\right)$ and $\left({\alpha }^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}{\zeta }^{\mathrm{<mo>\; *\; </mo>}}\right)$ is an optimal mixed regular-singular control.

For the proof of (i)-(x) of Theorem 2.1, refer to [1] and [7].

3. Application

We begin by considering four components that affect changes in the level of cash reserves of an insurance company under study and these are: premium payments, debt repayments, client claims and dividend pay-outs to shareholders. The first two components namely, premiums and debt repayments are deterministic and occur at a constant rate. Dividend payments are determined by the amount of cash reserves available at any given time. We also take into account the need for the company to mitigate risks arising from business through reinsurance. Reinsurance means controlling revenues by diverting a proportion $1-a$ of all premiums to another company, in which case $1-a$ fraction of each claim is paid by the other company [1].

Let $X\left(t\right)=X\left(t,\omega \right)\in \left[0,\infty \right]\times \Omega$ be a stochastic process on a filtered probability space $\left(\Omega \mathrm{,}\mathcal{F}\mathrm{,}{\mathcal{F}}_t\mathrm{,}P\right)$ representing the amount of liquid assets at time t. We fix a domain $S\subset \Re$ (our solvency region) and let the dynamics of $X\left(t\right)$ be modelled by the the following process:

$\text{d}X\left(t\right)=\left[\mu a\left(t\right)-\delta \right]\text{d}t+\sigma a\left(t\right)\text{d}B\left(t\right)+\gamma a\left(t\right){\displaystyle {\int }_{\Re }}z\tilde{N}\left(\text{d}t,\text{d}z\right)-\text{d}L\left(t\right)$ (3.1)

$X\left(0\right)=y$

where $\mu$ is the premium rate and is a positive constant, $\delta$ is the liability rate, $\sigma$ and $\gamma$ are positive constants, $\gamma z\le 0$ , $1-a\left(t\right)$ is the reinsurance fraction at time t, y is the initial value of the liquid assets of the company, $L\left(t\right)$ is the cumulative dividends paid up to time t, $B\left(t\right)$ is 1-dimensional Brownian Motion and $\tilde{N}\left(\text{d}t,\text{d}z\right)$ is a compensated Poisson process random measure with intensity $\lambda$ . In our model, we assume that:

(i) $B_t$ and the compensated Poisson process are independent;

(ii) the company has a policy to reinvest a proportion $\alpha$ of its excess cash; and

(iii) the company pays dividends when $x\ge \left(1+\frac{\beta }{1-\alpha }\right)x^{\mathrm{<mo>\; *\; </mo>}}$ .

where x is the amount of liquid assets at time t, $x^{\mathrm{<mo>\; *\; </mo>}}$ is a predetermined threshold, $\alpha$ is a proportion of the cash to be reinvested, $\beta \in \left(\mathrm{0,1}\right)$ and $\beta >\alpha$ .

The performance functional for this problem is given by

$J^{\tau \mathrm{,}y}\left(s\mathrm{,}\pi \right)=E^{s\mathrm{,}y}{\displaystyle {\int }_0^{\tau }}{\text{e}}^{-t\rho }\text{d}L\left(t\right)\mathrm{.}$ (3.2)

where ${\tau }_m^{\mathrm{<mo>\; *\; </mo>}}=\min \left\{\tau \mathrm{<mo>\; :\; </mo>}X\left(t\right)\le 0\right\}$ , that is, the first time that the state $X\left(t\right)$ reaches the value 0 or below. The problem is to find the optimal stopping time ${\tau }^{\mathrm{<mo>\; *\; </mo>}}$ , optimal control policy ${\pi }^{\mathrm{<mo>\; *\; </mo>}}=\left(a^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}{L}^{\mathrm{<mo>\; *\; </mo>}}\right)$ and value function $\varphi \left({\tau }^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}{\pi }^{\mathrm{<mo>\; *\; </mo>}}\right)$ that maximises the expected total discounted dividend payout. In other words we want ${\tau }^{\mathrm{<mo>\; *\; </mo>}}$ and ${\pi }^{\mathrm{<mo>\; *\; </mo>}}$ such that:

$\varphi \left({\tau }^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}{\pi }^{\mathrm{<mo>\; *\; </mo>}}\right)=\underset{\tau \mathrm{,}y}{\sup }J\left(\tau \mathrm{,}\pi \right)=J_y\left({\tau }^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}{\pi }^{\mathrm{<mo>\; *\; </mo>}}\right)\mathrm{.}$ (3.3)

In this model, we will take ${\tau }^{\mathrm{<mo>\; *\; </mo>}}$ as the time at which the company stops payment of dividends to shareholders. The optimal stopping time is determined by the level of liquid assets available.

4. Main Result

In the model, the barrier strategy is used to payout dividends. Dividend payments are only made when the amount of liquid assets or cash reserves available exceed a particular pre-determined level.

Lemma 4.1. Suppose the value of the initial liquid assets is 0, that is, $X\left(0\right)=0$ . Then $L\left(0\right)=0$ , $J_0\left({\tau }^{*},{\pi }^{*}\right)=0$ , for all $\pi \in A$ and $\tau =\inf \left\{t\ge 0:X\left(t\right)\le 0\right\}=0$ . The optimal strategy in this case is ${\tau }^{*}=0,{\pi }^{*}=\left(a^{*},0\right)$ where $a^{\mathrm{<mo>\; *\; </mo>}}$ is arbitrary.

Lemma 4.2. Assume $\mu \le \delta$ , then $\varphi \left({\tau }^{*},{\pi }^{*}\right)=y$ , $L^{*}\left(t\right)=y$ , ${\tau }^{*}=0$ and $a^{\mathrm{<mo>\; *\; </mo>}}$ is arbitrary.

Proof. Suppose ${\pi }^{\mathrm{<mo>\; *\; </mo>}}=\left(a^{\mathrm{<mo>\; *\; </mo>}}\left(\mathrm{.}\right)\mathrm{,}{L}^{\mathrm{<mo>\; *\; </mo>}}\left(\mathrm{.}\right)\right)$ with $L^{\mathrm{<mo>\; *\; </mo>}}\left(\mathrm{.}\right)=y$ and $a\left(t\right)$ arbitrary. If $\mu \le \delta$ , then it is optimal to immediately distribute the initial cash reserve $X\left(0\right)=y$ sometimes called “take the money and run away strategy”. We have

$\varphi \left({\tau }^{*},{\pi }^{*}\right)=y\text{and}{L}^{*}\left(t\right)=y$

We note that ${\tau }^{*}=\inf \left\{t\ge 0:X\left(t\right)\le 0\right\}=0$ . We then want to show that $J_y\left(\pi \right)\le y$ .

Let $X\left(\mathrm{.}\right)$ be the state trajectory corresponding to any given control $\pi =\left(a\left(\mathrm{.}\right)\mathrm{,}L\left(\mathrm{.}\right)\right)$ . From (3.1), we have

${\displaystyle {\int }_0^t}\text{d}X\left(s\right)={\displaystyle {\int }_0^t}\left(\mu a\left(s\right)-\delta \right)\text{d}t+{\displaystyle {\int }_0^t}\sigma a\left(s\right)\text{d}B\left(s\right)+\gamma a\left(s\right){\displaystyle {\int }_0^t}{\displaystyle {\int }_{ℝ}}z\tilde{N}\left(\text{d}s,\text{d}z\right)-{\displaystyle {\int }_0^t}\text{d}L(\; s\; )$

where $\mu a\left(s\right)-\delta \le 0$ . The preceding equation can be written as

${\displaystyle {\int }_0^t}\text{d}X\left(s\right)+{\displaystyle {\int }_0^t}\text{d}L\left(s\right)={\displaystyle {\int }_0^t}\left(\mu a\left(s\right)-\delta \right)\text{d}t+{\displaystyle {\int }_0^t}\sigma a\left(s\right)\text{d}B\left(s\right)+\gamma a\left(s\right){\displaystyle {\int }_0^t}{\displaystyle {\int }_{ℝ}}z\tilde{N}\left(\text{d}s,\text{d}z\right)\mathrm{.}$

Integrating LHS gives

$X\left(t\right)-X\left(0\right)+L\left(t\right)-L\left(0^{-}\right)=H\left(t\right).$ (4.1)

where

$H\left(t\right)={\displaystyle {\int }_0^t}\left(\mu a\left(s\right)-\delta \right)\text{d}t+{\displaystyle {\int }_0^t}\sigma a\left(s\right)\text{d}B\left(s\right)+\gamma a\left(s\right){\displaystyle {\int }_0^t}{\displaystyle {\int }_R}z\tilde{N}\left(\text{d}s,\text{d}z\right).$ (4.2)

But $H\left(t\right)=X\left(t\right)-X\left(0\right)+L\left(t\right)-L\left(0^{-}\right)$ is a supermartingale (See (4.46)). We have

$J_y\left(\pi \right)=E{\displaystyle {\int }_0^{\tau }}{\text{e}}^{-\gamma t}\text{d}L\left(t\right)=E{\displaystyle {\int }_0^{\tau }}{\text{e}}^{-\gamma t}\text{d}\left(H\left(t\right)-X\left(t\right)+X\left(0\right)+L\left(0^{-}\right)\right)$ (4.3)

after substituting for $L\left(t\right)$ . This implies that

$J_y\left(\pi \right)=E{\displaystyle {\int }_0^{\tau }}{\text{e}}^{-\gamma t}\text{d}H\left(t\right)-E{\displaystyle {\int }_0^{\tau }}{\text{e}}^{-\gamma t}\text{d}X\left(t\right)$ (4.4)

since $x\left(0\right)$ and $L\left(0^{-}\right)$ are constants. We have

$J_y\left(\pi \right)\le -E{\displaystyle {\int }_0^{\tau }}{\text{e}}^{-\gamma t}\text{d}X\left(t\right)\mathrm{.}$ (4.5)

Integrating by parts RHS of inequality (4.5), we obtain

$\begin{array}{c}{J}_y\left(\pi \right)\le -E{\left[X\left(t\right){\text{e}}^{-\gamma t}\right]}_0^{\tau }-\gamma E{\displaystyle {\int }_0^{\tau }}{\text{e}}^{-\gamma t}X\left(t\right)\text{d}t\\ =y-x\left(\tau \right){\text{e}}^{-\gamma \tau }-\gamma E{\displaystyle {\int }_0^{\tau }}{\text{e}}^{-\gamma t}X\left(t\right)\text{d}t\le y.\end{array}$

We have proved that for $\mu \le \delta$ , the optimal dividend payment is the initial wealth or cash reserve y, optimal stopping time ${\tau }^{\mathrm{<mo>\; *\; </mo>}}=0$ and the optimal policy ${\pi }^{\mathrm{<mo>\; *\; </mo>}}=\left(a^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}y\right)$ .

We now consider the non-trivial case where $\mu \ge \delta$ and we want to find the optimal stopping time and optimal policy that maximises the expected total discounted dividend pay-out.

Lemma 4.3. Given that $a^{*}=0$ , it is prudent for the insurance company not to do business. It should immediately distribute the initial cash reserve as dividends. The optimal policy in this case is ${\tau }^{*}=0$ , $\varphi \left({\tau }^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}{\pi }^{\mathrm{<mo>\; *\; </mo>}}\right)=y$ and ${\pi }^{\mathrm{<mo>\; *\; </mo>}}=\left(\mathrm{0,}y\right)$ .

Proof. Let $D=\left\{\left(s,x\right):0\le x\le x^{*}\right\}$ where $x^{\mathrm{<mo>\; *\; </mo>}}$ is to be determined and $\tau =\inf \left\{t\ge \mathrm{0\; <mo>\; :\; </mo>}X\left(t\right)\notin D\right\}$ . Suppose $a^{*}=0$ , that is, the proportion of reinsurance is 100%. Then the dynamics of the cash reserve is given by

$\text{d}X\left(t\right)=-\delta \text{d}t-\text{d}L\left(t\right)\mathrm{.}$ (4.6)

Integrating with respect to t, we have:

${\displaystyle {\int }_0^t}\text{d}X\left(s\right)=-{\displaystyle {\int }_0^t}\delta \text{d}s-{\displaystyle {\int }_0^t}\text{d}L\left(s\right)$ (4.7)

$\Rightarrow X\left(t\right)-X\left(0\right)=-{\displaystyle {\int }_0^t}\delta \text{d}s-\left[L\left(t\right)-L\left(0\right)\right]$

$\Rightarrow X\left(t\right)=X\left(0\right)-{\displaystyle {\int }_0^t}\delta \text{d}s-L\left(t\right)+L(\; 0\; )$

$\Rightarrow X\left(t\right)=y-{\displaystyle {\int }_0^t}\delta \text{d}s+L\left(0\right)-L(\; t\; )$

$X\left(t\right)=y+L\left(0\right)-{\displaystyle {\int }_0^t}\delta \text{d}s-L\left(t\right).$

We note that $X\left(t\right)\to -\infty$ as $t\to \infty$ since y and $L\left(0\right)$ are constants. Hence, when $a=0$ , the company should not get into business.

Lemma 4.4. Suppose $a^{\mathrm{<mo>\; *\; </mo>}}\in \left(\mathrm{0,1}\right]$ , then the value function is given by $\varphi \left(s\mathrm{,}\pi \right)={\text{e}}^{-\rho s}\psi \left(x\right)$ where

$\psi \left(x\right)=\{\begin{array}{l}{A}_1\left({\text{e}}^{r_{1}x}-{\text{e}}^{r_{2}x}\right),\text{for}\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>\; 0}<x<x^{*}\\ A_3+x,\text{for}x>x^{*}\end{array}$

where

$x^{*}=\frac{2\left(\ln r_1-\ln r_2\right)}{r_2-r_1},$ (4.8)

$A_1=\frac{1}{r_1{\text{e}}^{r_1{x}^{*}}-r_2{\text{e}}^{r_2{x}^{*}}},$ (4.9)

$A_3=\frac{1}{r_1{\text{e}}^{r_1{x}^{*}}-r_2{\text{e}}^{r_2{x}^{*}}}\left({\text{e}}^{r_1{x}^{*}}-{\text{e}}^{r_2{x}^{*}}\right)-x^{*},$ (4.10)

${\tau }^{\mathrm{<mo>\; *\; </mo>}}=\inf \left\{t\ge \mathrm{0\; <mo>\; :\; </mo>}x\le \chi \right\}\mathrm{,}$ (4.11)

$L^{*}\left(t\right)\ge \chi -x^{*}=\frac{\beta }{1-\alpha }{x}^{*},$ (4.12)

where $\chi =\left(1+\frac{\beta }{1-\alpha }\right)x^{\mathrm{<mo>\; *\; </mo>}}$ , $\chi$ is the amount of cash reserves at time t, $\beta \in \left(\mathrm{0,1}\right)$ , $\alpha \in \left(\mathrm{0,1}\right)$ and $\beta >\alpha$ The optimal strategy in this case is to pay out dividends when $x\ge \chi$ .

Proof

Case 1 ( $a^{*}=1,\mu \ge \delta$ )

We consider the case $a^{*}=1$ , that is, the company takes maximal risk by retaining all the premiums. The dynamics of the cash reserve is given by

$\text{d}X\left(t\right)=\left[\mu -\delta \right]\text{d}t+\sigma \text{d}B\left(t\right)+\gamma {\displaystyle {\int }_{\Re }}z\tilde{N}\left(\text{d}t,\text{d}z\right)-\text{d}L\left(t\right)$ (4.13)

$X\left(0\right)=y.$

In the absence of dividend payments, the integrodifferential operator of $\varphi$ coincides with its generator given below

$\text{Ł}\left(\varphi \right)=\frac{\partial \varphi }{\partial s}+\left(\mu -\delta \right)\frac{\partial \varphi }{\partial x}+\frac{1}{2}{\sigma }^2\frac{\partial {\varphi }^2}{\partial x^2}+{\displaystyle {\int }_{\Re }}\left[\varphi \left(s\mathrm{,}x+\gamma z\right)-\varphi \left(s\mathrm{,}x\right)+\gamma z\frac{\partial \varphi }{\partial x}\right]v\left(\text{d}z\right)\mathrm{.}$

(4.14)

Inside the continuation region, $\varphi$ satisfies the following

$\max \left\{\frac{\partial \varphi }{\partial s}+\left(\mu -\delta \right)\frac{\partial \varphi }{\partial x}+\frac{1}{2}{\sigma }^2\frac{\partial {\varphi }^2}{\partial x^2}+{\displaystyle {\int }_{\Re }}\left[\varphi \left(s\mathrm{,}x+\gamma z\right)-\varphi \left(s\mathrm{,}x\right)+\gamma z\frac{\partial \varphi }{\partial x}\right]v\left(\text{d}z\right)\right\}=0.$

(4.15)

The non-intervention region D is described by

$D=\left\{\left(s\mathrm{,}x\right)\mathrm{<mo>\; :\; </mo>}\kappa \frac{\partial \varphi }{\partial x}+\theta \le 0\right\}$ (4.16)

where $\kappa \mathrm{<mo>\; :\; </mo>}ℝ\to ℝ$ and $\theta \mathrm{<mo>\; :\; </mo>}ℝ\to ℝ$ .

This implies that $D=\left\{\left(s\mathrm{,}x\right)\mathrm{<mo>\; :\; </mo>}-\frac{\partial \varphi }{\partial x}+{\text{e}}^{-\rho s}\le 0\right\}$ since $\kappa =-1$ and $\theta ={\text{e}}^{-\rho s}$ .

We guess that D has the form $D=\left\{\left(s\mathrm{,}x\right)\mathrm{<mo>\; :\; </mo>\; 0}\le x\le x^{\mathrm{<mo>\; *\; </mo>}}\right\}$ for some $x^{\mathrm{<mo>\; *\; </mo>}}\ge 0$ .

Inside D, we must have $L\varphi \left(s\mathrm{,}x\right)+f\left(s\mathrm{,}x\right)=0$ . We have

$L\varphi \left(s\mathrm{,}x\right)=0$ (4.17)

since $f\left(s\mathrm{,}x\right)=0$ . We try a solution $\varphi$ of the form $\varphi \left(s\mathrm{,}x\right)={\text{e}}^{-\rho s}\psi \left(x\right)$ and substituting into (4.17), we obtain:

$\begin{array}{l}-\rho \psi \left(x\right)+\left(\mu -\delta \right){\psi }^{\prime }\left(x\right)+\frac{1}{2}{\sigma }^2{\psi }^{″}\\ +{\displaystyle {\int }_{ℝ}}\left\{\psi \left(s\mathrm{,}x+\gamma z\right)-\psi \left(s\mathrm{,}x\right)-\gamma z{\psi }^{\prime }\left(x\right)\right\}v\left(\text{d}z\right)=0.\end{array}$

We consider $\psi \left(x\right)={\text{e}}^{rx}$ for some constant $r\in ℝ$ . Substituting into the preceding equation, we get:

$h\left(r\right)=-\rho +r\left(\mu -\delta \right)+\frac{1}{2}{\sigma }^2{r}^2+{\displaystyle {\int }_{ℝ}\left\{{\text{e}}^{r\gamma z}-1-\gamma zr\right\}v\left(\text{d}z\right)}=0.$ (4.18)

We note that $h\left(0\right)=-\rho <0$ and $h\left(r\right)\to \infty$ as $r\to \infty$ . This implies that the equation $h\left(r\right)$ has two solutions $r_1\mathrm{,}{r}_2$ such that $r_2<0<r_1$ .

Outside D, we require that

$-{\psi }^{\prime }\left(x\right)+1=0.$ (4.19)

Integrating Equation (4.19) with respect to x yields

$\psi \left(x\right)=x+A_3\mathrm{.}$ (4.20)

Hence we put

$\psi \left(x\right)=\{\begin{array}{l}{A}_1{\text{e}}^{r_{1}x}+A_2{\text{e}}^{r_{2}x},\text{for}0<x<x^{*}\\ A_3+x,\text{for}x>x^{*}\end{array}$

To find $A_1\mathrm{,}{A}_3$ and $x^{\mathrm{<mo>\; *\; </mo>}}$ , we use the “high contact” principle also called the smooth-pasting condition of singular control which dictates that the value function should be $C^2$ , in particular at the free boundary $x^{\mathrm{<mo>\; *\; </mo>}}$ . Now $\psi \left(0\right)=0$ implies that $A_1+A_2=0$ . This gives $A_2=-A_1$ . We have

$\psi \left(x\right)=\{\begin{array}{l}{A}_1\left({\text{e}}^{r_{1}x}-{\text{e}}^{r_{2}x}\right),\text{for}0<x<x^{*}\\ A_3+x,\text{for}x>x^{*}\end{array}$

Applying the “high contact” principle we have

$A_1\left({\text{e}}^{r_1{x}^{*}}-{\text{e}}^{r_{2}x*}\right)=A_3+x^{*},\left(\text{continuity}\text{at}{x}^{*}\right)$ (4.21)

${\psi }^{\prime }\in C^1\text{at}x=x^{*},\Rightarrow A_1\left(r_1{\text{e}}^{r_1{x}^{*}}-r_2{\text{e}}^{r_2{x}^{*}}\right)=1$ (4.22)

${\psi }^{″}\in C^2\text{at}x=x^{*},\Rightarrow A_1\left(r_1^2{\text{e}}^{r_1{x}^{*}}-r_2^2{\text{e}}^{r_2{x}^{*}}\right)=0.$ (4.23)

From (4.23), we have $A_1{r}_1^2{\text{e}}^{r_1{x}^{*}}=A_1{r}_2^2{\text{e}}^{r_2{x}^{*}}$ . Dividing through by $A_1$ , we have

$r_1^2{\text{e}}^{r_1{x}^{*}}=r_2^2{\text{e}}^{r_2{x}^{*}}.$ (4.24)

Taking log of both sides of (4.24), we get

$2\ln r_1+r_1{x}^{*}=2\ln r_2+r_2{x}^{*}.$ (4.25)

From (4.25), we get:

$2\left(\ln r_1-\ln r_2\right)=\left(r_2-r_1\right)x^{\mathrm{<mo>\; *\; </mo>}}\mathrm{.}$ (4.26)

Making $x^{\mathrm{<mo>\; *\; </mo>}}$ subject of the formula in (4.26), we have

$x^{\mathrm{<mo>\; *\; </mo>}}=\frac{2\left(\ln r_1-\ln r_2\right)}{r_2-r_1}\mathrm{.}$ (4.27)

Substituting for $x^{\mathrm{<mo>\; *\; </mo>}}$ in (4.22) gives

$A_1=\frac{1}{r_1{\text{e}}^{r_1{x}^{*}}-r_2{\text{e}}^{r_2{x}^{*}}}$ (4.28)

where $x^{\mathrm{<mo>\; *\; </mo>}}$ is as in (4.27). Substituting for $x^{\mathrm{<mo>\; *\; </mo>}}$ and $A_1$ in (4.21) yields

$A_3=\frac{1}{r_1{\text{e}}^{r_1{x}^{*}}-r_2{\text{e}}^{r_2{x}^{*}}}\left({\text{e}}^{r_1{x}^{*}}-{\text{e}}^{r_2{x}^{*}}\right)-x^{*}.$ (4.29)

Since the company has an investment policy to reinvest a proportion $\alpha$ of its surplus cash, the optimal strategy is to pay out dividends when

$\left(x-x^{\mathrm{<mo>\; *\; </mo>}}\right)-\alpha \left(x-x^{\mathrm{<mo>\; *\; </mo>}}\right)\ge \beta x^{\mathrm{<mo>\; *\; </mo>}}\mathrm{.}$ (4.30)

Solving the inequality for x gives

$x\ge \frac{1-\alpha +\beta }{1-\alpha }{x}^{*}=\left(1+\frac{\beta }{1-\alpha }\right)x^{*}.$ (4.31)

We want to show that $\varphi \left(s\mathrm{,}x\right)={\text{e}}^{-\rho s}\psi \left(x\right)$ satisfies the conditions of the verification theorem for all the values of $A_1$ and $A_3$ .

We have constructed $\varphi$ such that $L\varphi +f=0$ in D. Outside D, that is for $x>x^{*}$ , we have

$L\varphi \left(s,x\right)+f\left(s,x\right)=L\psi \left(x\right)$ . This can be written as:

$\begin{array}{l}L\psi \left(x\right)=\rho \left(A_3+x\right)+\left(\mu -\delta \right)\\ +{\displaystyle {\int }_{x+\gamma z<x^{*}}}\left\{A_1\left({\text{e}}^{r_1\left(x+\gamma z\right)}-{\text{e}}^{r_2\left(x+\gamma z\right)}\right)-\left(x+\gamma z+A_3\right)\right\}v(\; d\; z\; )\end{array}$

since at $x=x^{*}$ , $A_1\left({\text{e}}^{r_{1}x}-{\text{e}}^{r_{2}x}\right)=A_3+x$ .

We have $L\psi \left(x\right)\le -\rho A_3-\rho x+\left(\mu -\delta \right)$ which is decreasing in x. From our construction, we have $L\psi \left(x\right)\le 0$ for $x\ge x^{\mathrm{<mo>\; *\; </mo>}}$ and $L\psi \left(x\right)=0$ for $x<x^{*}$ . Therefore we must have $L\psi \left(x\right)=0$ at $x=x^{*}$ .

Case 2 ( $a\in \left(\mathrm{0,1}\right)\mathrm{,}\mu \ge \delta$ )

We assume $a^{\mathrm{<mo>\; *\; </mo>}}\in \left(\mathrm{0,1}\right)$ . Inside the continuation region D, $\varphi$ satisfies $\max \left\{L\varphi \left(s\mathrm{,}x\right)+f\left(s\mathrm{,}x\right)\right\}=0$ . That is

$\begin{array}{l}\max \{\frac{\partial \varphi }{\partial s}+\left(\mu a-\delta \right)\frac{\partial \varphi }{\partial x}+\frac{1}{2}{\sigma }^2{a}^2\frac{\partial {\varphi }^2}{\partial x^2}\\ +{\displaystyle {\int }_{\Re }}\left[\varphi \left(s\mathrm{,}x+a\gamma z\right)-\varphi \left(s\mathrm{,}x\right)+a\gamma z\frac{\partial \varphi }{\partial x}\right]v\left(\text{d}z\right)\}=0.\end{array}$

since $f\left(s\mathrm{,}x\right)=0$ . We try a solution of the form $\varphi \left(s\mathrm{,}x\right)={\text{e}}^{-\rho s}\psi \left(x\right)$ . Substituting it into the preceding equation, we obtain:

$\begin{array}{l}\max \{-\rho {\text{e}}^{-\rho s}\psi \left(x\right)+\left(\mu a-\delta \right){\text{e}}^{-\rho s}{\psi }^{\prime }\left(x\right)+\frac{1}{2}{a}^2{\sigma }^2{\text{e}}^{-\rho s}{\psi }^{″}\left(x\right)\\ \underset{}{\overset{}{}}+{\displaystyle {\int }_{\Re }}\left\{{\text{e}}^{-\rho s}\psi \left(x+\gamma az\right)-{\text{e}}^{-\rho s}\psi \left(x\right)-\gamma az{e}^{-\rho s}{\psi }^{\prime }\left(x\right)\right\}v\left(\text{d}z\right)\}=0\end{array}$

In particular, we try a solution of the form $\psi \left(x\right)=M{\text{e}}^{rx}$ and substitute it into the above equation to get;

$h\left(r\right)=-\rho +r\left(\mu a-\delta \right)+\frac{1}{2}{a}^2{\sigma }^2{r}^2+{\displaystyle {\int }_{\Re }}\left\{{\text{e}}^{r\gamma az}-1-\gamma azr\right\}v\left(\text{d}z\right)=0.$ (4.32)

In the no jump case, that is, $v=0$ , the maximum value of a is attained at

$\mu \frac{\partial \varphi }{\partial x}+a^{*}{\sigma }^2\frac{\partial {\varphi }^2}{\partial x^2}=0.$ (4.33)

Solving for $a^{\mathrm{<mo>\; *\; </mo>}}$ gives

$a^{*}=\frac{-\mu \frac{\partial \varphi }{\partial x}}{{\sigma }^2\frac{{\partial }^2\varphi }{\partial x^2}}.$ (4.34)

In the jump case, the value of a is attained at the critical point $\frac{\text{d}h}{\text{d}a}=0$ .

Differentiating with respect to a and equating to 0 yields

$\frac{\text{d}h}{\text{d}a}=r\mu +a{\sigma }^2{r}^2+{\displaystyle {\int }_{\Re }}\left\{r\gamma z{\text{e}}^{ar\gamma z}-r\gamma z\right\}v\left(\text{d}z\right)=0.$

Dividing through byr, we obtain

$\frac{\text{d}h}{\text{d}a}=\mu +a{\sigma }^{2}r+{\displaystyle {\int }_{\Re }}\left\{\gamma z{\text{e}}^{ar\gamma z}-\gamma z\right\}v\left(\text{d}z\right)=0.$

We let:

$H\left(a\right)=\mu +a{\sigma }^{2}r-\gamma {\displaystyle {\int }_{\Re }}\left\{1-{\text{e}}^{ar\gamma z}\right\}zv\left(\text{d}z\right)=0.$ (4.35)

Substituting for $a=0$ in (4.35), we have $H\left(0\right)=\mu >0$ We note that

$H\left(1\right)=\mu +r{\sigma }^2-\gamma {\displaystyle {\int }_{\Re }}\left\{1-{\text{e}}^{r\gamma z}\right\}zv\left(\text{d}z\right).$

$H\left(1\right)$ can be written as

$H\left(1\right)=\mu -\left(-r{\sigma }^2+\gamma {\displaystyle {\int }_{\Re }}\left\{1-{\text{e}}^{r\gamma z}\right\}zv\left(\text{d}z\right)\right).$

Suppose $-r{\sigma }^2+\gamma {\displaystyle {\int }_{\Re }}\left\{1-{\text{e}}^{r\gamma z}\right\}zv\left(\text{d}z\right)>\mu$ , then there exists an optimal $a^{\mathrm{<mo>\; *\; </mo>}}\in \left(\mathrm{0,1}\right]$ such that

$-\rho +r\left(\mu a^{*}-\delta \right)+\frac{1}{2}{a}^{*}{}^2{\sigma }^2{r}^2+{\displaystyle {\int }_{\Re }}\left\{{\text{e}}^{zr\gamma a^{*}}-1-a^{*}\gamma zr\right\}v\left(\text{d}z\right)=0.$ (4.36)

We take $a^{\mathrm{<mo>\; *\; </mo>}}$ as constant. For this value of $a=a^{*}$ , the cash dynamics of the company is given by

$\text{d}X\left(t\right)=\left(\mu a^{*}-\delta \right)\text{d}t+\sigma a^{*}\text{d}B\left(t\right)+\gamma a^{*}{\displaystyle {\int }_{\Re }}z\tilde{N}\left(\text{d}t,\text{d}z\right)-\text{d}L\left(t\right)$ (4.37)

$X\left(0\right)=x.$

We guess that the continuation region is given by $D=\left\{\left(s\mathrm{,}x\right)\mathrm{<mo>\; :\; </mo>\; 0\; <mo>\; <\; </mo>}x\le x^{\mathrm{<mo>\; *\; </mo>}}\right\}$ as in case 1. Inside the continuation region, we must have $\max \left\{L_1\varphi \left(x\right)+f\left(s\mathrm{,}x\right)\right\}=0$ . This implies that

$\begin{array}{l}\max \{\frac{\partial \varphi }{\partial s}+\left(\mu a^{\mathrm{<mo>\; *\; </mo>}}-\delta \right)\frac{\partial \varphi }{\partial x}+\frac{1}{2}{a}^{\mathrm{<mo>\; *\; </mo>}}{}^2{\sigma }^2\frac{\partial {\varphi }^2}{\partial x^2}\\ +{\displaystyle \int }\left[\varphi \left(s\mathrm{,}x+\gamma a^{\mathrm{<mo>\; *\; </mo>}}z\right)-\varphi \left(s\mathrm{,}x\right)+\gamma a^{\mathrm{<mo>\; *\; </mo>}}z\frac{\partial \varphi }{\partial x}\right]v\left(\text{d}z\right)\}=0.\end{array}$

We try a solution of the form $\varphi \left(x\right)={\text{e}}^{-\rho s}\phi \left(x\right)$ . Substituting this last equation and simplifying gives

$\begin{array}{l}-\rho \phi \left(x\right)+\left(\mu a^{\mathrm{<mo>\; *\; </mo>}}-\delta \right){\phi }^{\prime }\left(x\right)+\frac{1}{2}{\sigma }^2{\phi }^{″}\\ +{\displaystyle {\int }_{\Re }}\left\{\phi \left(x+\gamma a^{\mathrm{<mo>\; *\; </mo>}}z\right)-\phi \left(x\right)-\gamma a^{\mathrm{<mo>\; *\; </mo>}}z{\phi }^{\prime }\left(x\right)\right\}v\left(\text{d}z\right)=0.\end{array}$

Consider the function $\phi \left(x\right)={\text{e}}^{\lambda x}$ and substitute into the last equation to get;

$-\rho +\left(\mu a^{\mathrm{<mo>\; *\; </mo>}}-\delta \right)\lambda +\frac{1}{2}{\sigma }^2{\lambda }^2{a}^{\mathrm{<mo>\; *\; </mo>}}{}^2+{\displaystyle {\int }_{\Re }}\left\{{\text{e}}^{\lambda \gamma a^{\mathrm{<mo>\; *\; </mo>}}z}-1-\gamma \lambda a^{\mathrm{<mo>\; *\; </mo>}}z\right\}v\left(\text{d}z\right)=0.$

Define

$h\left(\lambda \right)=-\rho +\left(\mu a^{\mathrm{<mo>\; *\; </mo>}}-\delta \right)\lambda +\frac{1}{2}{\sigma }^2{\lambda }^2{a}^{\mathrm{<mo>\; *\; </mo>}}{}^2+{\displaystyle {\int }_{\Re }}\left\{{\text{e}}^{\lambda \gamma a^{\mathrm{<mo>\; *\; </mo>}}z}-1-\gamma \lambda a^{\mathrm{<mo>\; *\; </mo>}}z\right\}v(\; d\; z\; )$

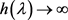$h\left(0\right)=-\rho <0$ and as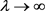. Therefore, there exists.

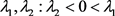Outside D, we require as in case 1 that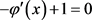. Integrating with respect to x gives.

We now determine 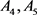and.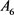

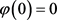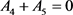
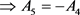gives . We have

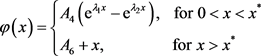
Applying the “smooth fit” principle as in case 1, we obtain

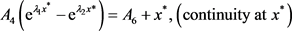(4.38)

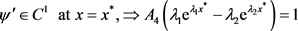(4.39)

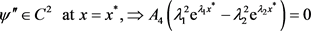(4.40)

As in case 1, we have

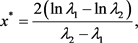(4.41)

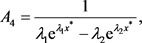(4.42)

where 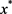is as in (4.41). Substituting for 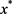and in (4.38) yields

(4.43)

(4.44)

(4.45)

where. The optimal strategy in this case is to pay out dividends only when. We can write the optimal strategy as where and are as in (4.44) and (4).

Theorem 4.1. Fix any initial condition and consider the problem of maximising the performance criterion over all dividend strategies. The value function is increasing. The following cases provide the solution to the control problem:

(i) If, then, , , for all and and is arbitrary.

(ii). If, then and.

(iii). If, then the optimal dividend strategy is to immediately distribute the initial cash reserve as dividends. The optimal strategy in this case is, and.

(iv). Suppose and, then, where, and. The optimal strategy is to pay out dividends when the available amount of cash reserves exceed.

Lemma 4.5. Suppose that. Then is a super-martingale where

(4.46)

Proof. Let. We have

since from (4.46), , and, are constants. We conclude that is a super-martingale.

5. Numerical Analysis

In this section, we present and analyse the results obtained in Section 4 using numerical examples. The four tables below illustrate the effect of changes in the parameters on the value function, the predetermined threshold in the barrier strategy, the optimal dividend policy and the reinvestment policy.

In Table 1 consider the case when, , , , , , , , and.

In this case, dividends are only paid when the amount of liquid assets at time t is at least equal to 45.5.

In Table 2 consider the case when, , , , , , , , and.

In the case under consideration, the company should pay dividends when the amount of liquid assets at time t is at least equal to 57.8.

Table 1. Value function versus amount of liquid assets.

In Table 3 if, , , , , , , and.

The value function attains the maximum value at 465.9 when the amount of the available liquid assets is at least equal to 153.

Finally, in Table 4 consider, , , , , , , , and

In view of the company’s policy, it should only pay dividends when the amount of liquid assets is at least equal to 122.7.

Table 2. Value function versus amount of liquid assets.

Table 3. Value function versus amount of liquid assets.

Table 4. Value Function versus amount of liquid assets.

6. Conclusion

The results in this study have shown that there exists an optimal dividend policy for an insurance company that controls risk through proportional reinsurance, has a debt liability. Liquid assets dynamics is represented by a jump diffusion process and has a policy to reinvest a predetermined proportion of its excess cash. The main empirical findings of the paper are that when the premium rate is less than the liability rate, the company should not get into business and the optimal dividend policy is to immediately pay out the initial cash reserve as dividends to shareholders. While if the premium rate is more than the liability rate, the optimal risk management decisions depend on the current level of the cash reserves. The optimal dividend policy is to pay out dividends as the level of cash reserves is above a predetermined threshold. Further, the use of numerical examples clearly illustrated the effect of changes in the values of the parameters on the value function, the cash reserve threshold and the dividend payouts.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Chikodza, E. (2008) Combined Singular and Impulse Control for Jump Diffusions. Ph.D. Thesis, University of Zimbabwe, Harare.
[2]	Guo, X. (2003) A constrained non-linear regular singular control problem with application. Elsevier, Amsterdam.
[3]	He, L., Liang, Z. and Wu, J.L. (2010) Optimal Dividend and Reisurance Strategy of a Property Insurance Company under Catastrophe Risk. http://arxiv.org/1009.1269
[4]	Liu, B. (2004) Uncertain Theory. Springer-Verlag, Berlin.
[5]	ksendal, B. (2010) Optimal Stopping and Stochastic Control of Differential Games for Jump Diffusions. Centre of Maths for Applications, Norway.
[6]	Ksendal, B. (2009) Stochastic Differential Equations. Springer-Verlag, Berlin.
[7]	Ksendal, B. and Sulem, A. (2009) Applied Stochastic Control of Jump-Diffusions. Springer, Berlin.
[8]	Scheer, N. (2011) Optimal Stochastic Control of Dividends and Capital Injections. Ph.D. Thesis, Naturwissenschaftlichen Fakultat Der University, Koln.
[9]	Taksar, I. and Zhou, X. (1998) Optimal Risk and Dividend Control for a Company with a Debt Liability. Insurance: Mathematics and Economics, 22, 105-122. https://doi.org/10.1016/S0167-6687(98)00012-2
[10]	Zou, et al. (2009) Optimal Dividend Payments under Jump-Diffusion Risk Processes. Stochastic Models, 25, 332-347. https://doi.org/10.1080/15326340902870133
[11]	Yang, R. et al. (2005) Optimal Impulse and Regular Control Strategies for Proportional Reinsurance. Journal of Applied Maths and Computing, 18, Article No. 145. https://doi.org/10.1007/BF02936561