Asymptotic Analysis of Linear and Interval Linear Fractional-Order Neutral Delay Differential Systems Described by the Caputo-Fabrizio Derivative

Ann Al Sawoor, Miloud Sadkane

Laboratoire de Mathématiques de Bretagne Atlantique, CNRS-UMR 6205, Université de Brest, Brest Cedex 3, France.

DOI: 10.4236/am.2020.1112084                

Abstract

Asymptotic stability of linear and interval linear fractional-order neutral delay differential systems described by the Caputo-Fabrizio (CF) fractional derivatives is investigated. Using Laplace transform, a novel characteristic equation is derived. Stability criteria are established based on an algebraic approach and norm-based criteria are also presented. It is shown that asymptotic stability is ensured for linear fractional-order neutral delay differential systems provided that the underlying stability criterion holds for any delay parameter. In addition, sufficient conditions are derived to ensure the asymptotic stability of interval linear fractional order neutral delay differential systems. Examples are provided to illustrate the effectiveness and applicability of the theoretical results.

Keywords

Fractional Calculus, Caputo-Fabrizio Fractional Derivative, Neutral Delay Differential Systems, Asymptotic Stability

1. Introduction

Fractional calculus is attracting more and more researchers in applied sciences and engineering because of many advantages of fractional derivatives which provide important tools in modelling natural phenomena, see, e.g., [1] [2]. There are different types of fractional derivatives, those of Riemann-Liouville and Caputo are the most popular in the literature [3] [4] [5] [6].

In their recent work, Caputo and Fabrizio [7] introduced a new fractional order derivative with a nonsingular kernel, hereinafter called the fractional Caputo-Fabrizio (CF) derivative. This new fractional derivative is less affected by the past compared to the Caputo fractional derivative, which may exhibit slow stabilization [8]. The properties and numerical aspects of the CF derivative and their corresponding fractional integrals have been studied in [9] - [15]. In this paper, we are interested in linear and interval linear fractional-order neutral delay differential equations described by the CF derivative. Recently, a great attention has been paid to fractional delay differential systems. One of the most important research topics of the theory of such systems is the stability analysis. However, in the literature cited above, there are only few results (see, e.g., [8] [16] ) on this topic. In [17] the authors study the stability analysis of linear fractional-order ordinary differential equations described by the CF derivative, whereas the authors of [18] consider the stability analysis of linear fractional-order systems with time delay, establish a characteristic equation using the Laplace transform and provide some brief sufficient stability conditions. In [19] the authors consider the asymptotic stability for uncertain singular neutral delay systems and in [20] [21] [22] the authors study the stability analysis of interval linear fractional ordinary differential systems, interval linear fractional neutral differential systems described by the Caputo derivative and interval linear fractional neutral differential-algebraic systems described by the Caputo derivative, respectively. While being different, we extend the analysis carried out in the above cited references. We apply a spectrum based approach to establish asymptotic stability criteria for fractional-order neutral delay differential systems and the novelty of this work lies in the following aspects. Firstly, the CF definition of the fractional derivative is applied to analyze linear and interval linear fractional-order differential systems including neutral time delay. Secondly, by using the Laplace transform, we establish a novel characteristic equation. Thirdly, we apply an algebraic approach to establish sufficient asymptotic stability criteria ensuring that all the roots of characteristic equation lie in open left half of the complex plane. Fourthly, we present sufficient norm criteria to ensure the asymptotic stability of such systems. A nice consequence is that these stability criteria avoid solving the characteristic (transcendental) equation.

The rest of the paper is organized as follows: In Section 2 we formulate the problem and introduce the notation that will be used throughout the paper. In Section 3 we establish the main results for the asymptotic stability criteria for linear and interval linear fractional neutral delay differential equations. Finally, some concluding remarks are given in Section 4.

2. Problem Formulation and Notation

We consider linear fractional-order neutral delay differential systems of the form

${}_{CF}D{}^{\alpha }\left[y\left(t\right)-Cy\left(t-\tau \right)\right]=Ay\left(t\right)+By\left(t-\tau \right),t\ge 0,$ (1)

$y\left(t\right)=\phi \left(t\right),-\tau \le t\le 0$

where $0<\alpha <1$, $y\left(t\right)$ is a real vector of size n (the state vector); A, B and C are real $n\times n$ matrices; $\tau$ is a positive parameter (the time delay) and $\phi$ is a consistent initial function. The notation ${}_{CF}D{}^{\alpha }z\left(t\right)$ stands for Caputo–Fabrizio fractional order derivative of order $\alpha$ of z(t) defined by (see [7] )

${}_{CF}D{}^{\alpha }z\left(t\right)=\frac{{\text{d}}^{\alpha }z\left(t\right)}{\text{d}{t}^{\alpha }}=\frac{1}{1-\alpha }{\displaystyle {\int }_0^t\exp }\left(-\frac{\alpha }{1-\alpha }\left(t-\mu \right)\right)\frac{\text{d}z\left(\mu \right)}{\text{d}t}\text{d}\mu \text{.}$

We study two cases. In the first case the matrices A, B, and C are constant and in the second case they are interval matrices, that is

$A=\left\{\left(a_{ij}\right):a_{ij}^{\left(1\right)}\le a_{ij}\le a_{ij}^{\left(2\right)},i,j=1,2,\cdots ,n\right\},$ (2a)

$B=\left\{\left(b_{ij}\right):b_{ij}^{\left(1\right)}\le b_{ij}\le b_{ij}^{\left(2\right)},i,j=1,2,\cdots ,n\right\},$ (2b)

$C=\left\{\left(c_{ij}\right):c_{ij}^{\left(1\right)}\le c_{ij}\le c_{ij}^{\left(2\right)},i,j=1,2,\cdots ,n\right\},$ (2c)

where $a_{ij}^{\left(k\right)},b_{ij}^{\left(k\right)}$ and $c_{ij}^{\left(k\right)},k=1,2$ are given. The equations associated with the constant and interval cases will be denoted respectively by (LFNDDE) and (ILFNDDE). When a property applies equally to both cases (as in Definition 1 for example), the corresponding system will simply be referred to as system (1).

The following notation will be used throughout the paper. For a square complex matrix X,

$X^{*}$ denotes conjugate transpose of X,

$\det \left(X\right)$ denotes the determinant of X,

$\rho \left(X\right)$ denotes the spectral radius of X,

$\Vert X\Vert$ denotes the spectral norm of X;

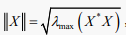, where ${\lambda }_{\max }$ is the largest eigenvalue,

$\Vert X\Vert =\rho \left(X\right)$ (if X is Hermitian, that is, if $X=X^{\text{*}}$ )

$\mu \left[X\right]$ denotes the logarithmic norm ofX;

$\mu \left(X\right)=\frac{1}{2}{\lambda }_{\max }\left(X+X^{*}\right)$, where ${\lambda }_{\max }$ is the largest eigenvalue,

$\mu \left(X\right)={\lambda }_{\max }\left(X\right)$ (if X is Hermitian, that is, if $X=X^{\text{*}}$ )

If $X=\left(x_{ij}\right)\in C^{n\times n}$, we set $\left|X\right|=\left(\left|x_{ij}\right|\right)$. If $X=\left(x_{ij}\right)\in R^{n\times n}$ and $Y=\left(y_{ij}\right)\in R^{n\times n}$, the inequality $X\le Y$ means that $x_{ij}\le y_{ij}$ for $i,j=1,\cdots ,n$.

The following inequalities, which will be used in the sequel, can be found in the literature, see, e.g., [23]. If $U,V\in C^{n\times n}$ and $W\in R^{n\times n}$ with $\left|U\right|\le W$, then

$\rho \left(U+V\right)\le \rho \left(\left|U+V\right|\right)\le \rho \left(\left|U\right|+\left|V\right|\right)\le \rho \left(W+\left|V\right|\right),$

$Re\left(\lambda \left(U\right)\right)\le \mu \left(U\right)$ for any eigenvalue $\lambda \left(U\right)$ of U,

$\mu \left(U+V\right)\le \mu \left(U\right)+\mu \left(V\right),\mu \left(U\right)\le \Vert U\Vert ,\rho \left(U\right)\le \Vert U\Vert \text{.}$

3. Main Results

Applying the Laplace transform to (1), we obtain

$\frac{1}{1-\alpha }\frac{1}{s+\frac{\alpha }{1-\alpha }}\left(I-C{\text{e}}^{-s\tau }\right)\left(sY\left(s\right)-y\left(0\right)\right)=AY\left(s\right)+B{\text{e}}^{-s\tau }Y\left(s\right),$

where $Y\left(s\right)$ is the Laplace transform of $y\left(t\right)$ for $t\ge 0$, defined by

$Y\left(s\right)={\displaystyle {\int }_0^{\infty }y}\left(t\right){\text{e}}^{-st}\text{d}t.$

This leads after rearrangement to

$P\left(s\right)Y\left(s\right)=\left(I-C{\text{e}}^{-s\tau }\right)y\left(0\right),$ (3)

where

$P\left(s\right)=s\left(I-C{\text{e}}^{-s\tau }-\left(1-\alpha \right)\left(A+B{\text{e}}^{-s\tau }\right)\right)-\alpha \left(A+B{\text{e}}^{-s\tau }\right)$.

The characteristic equation of (1) is defined by

$Q\left(s,\tau \right)=\det \left(P\left(s\right)\right)=0.$ (4)

As we will see, it plays an important role in the stability analysis of system (1).

Definition 1. The zero solution $y\left(t\right)=0$ of system (1) is said to be asymptotically stable if for any consistent $\phi \in \text{C}\left(\left[-\tau ,0\right],R^n\right)$ its analytic solution $y\left(t\right)$ satisfies ${\lim }_{t\to \infty }y\left(t\right)=0$ for any delay parameter $\tau >0$.

From Definition 1 we obtain the following theorem whose proof is similar to that given in [24].

Theorem 1. System (1) is asymptotically stable if the roots of the characteristic equation (4) lie in the open left half of the complex plane and are uniformly bounded away from the imaginary axis.

Next, several sufficient conditions of stability of system (1) are given.

Lemma 1. If the family of matrices $\left\{A,B,C\right\}$ defined in (LFNDDE) satisfies the conditions

(C₁) $\det \left[s{\left(s\left(1-\alpha \right)+\alpha \right)}^{-1}\left(I-C\right)-\left(A+B\right)\right]\ne 0$, for $Re\left(s\right)\ge 0$,

(C₂) $\underset{Re\left(s\right)\ge 0}{\sup }\rho \left[{\left(s{\left(s\left(1-\alpha \right)+\alpha \right)}^{-1}\left(I-C\right)-\left(A+B\right)\right)}^{-1}\left(B+s{\left(s\left(1-\alpha \right)+\alpha \right)}^{-1}C\right)\right]<\frac{1}{2}$

Then, for all $s\in C$ such that $Re\left(s\right)\ge 0$

(C₃) $Q\left(s,\tau \right)\ne 0.$

Proof. To simplify the notation, let us denote by

$\begin{array}{l}\gamma \left(s\right)={\left(s\left(1-\alpha \right)+\alpha \right)}^{-1},\\ K\left(s\right)={\left(s\gamma \left(s\right)\left(I-C\right)-\left(A+B\right)\right)}^{-1}\left(B+s\gamma \left(s\right)C\right).\end{array}$

The condition (C₂) can then be written

${\sup }_{Re\left(s\right)\ge 0}\rho \left(K\left(s\right)\right)<\frac{1}{2}$.

We have

$P\left(s\right)=s\left(I-C{\text{e}}^{-s\tau }-\left(1-\alpha \right)\left(A+B{\text{e}}^{-s\tau }\right)\right)-\alpha \left(A+B{\text{e}}^{-s\tau }\right)$

$\begin{array}{c}=\left(s\gamma \left(s\right)\left(I-C{\text{e}}^{-s\tau }\right)-(A+B{\text{e}}^{-s\tau })\right)\gamma {\left(s\right)}^{-1}\\ =\left(s\gamma \left(s\right)\left(I-C\right)-\left(A+B\right)\right)-\left(B+s\gamma \left(s\right)C\right)\left({\text{e}}^{-s\tau }-1\right)\gamma {\left(s\right)}^{-1}\\ =\left(s\gamma \left(s\right)\left(I-C\right)-\left(A+B\right)\right)\left(I-K\left(s\right)\left({\text{e}}^{-s\tau }-1\right)\right)\text{.}\end{array}$

The condition (C₁) ensures that $s\gamma \left(s\right)\left(I-C\right)-\left(A+B\right)$ is nonsingular and the condition (C₂) ensures that $\rho \left[K\left(s\right)\left({\text{e}}^{-s\tau }-1\right)\right]<1$ and hence $I-K\left(s\right)\left({\text{e}}^{-s\tau }-1\right)$ is nonsingular. Therefore, (C₃) is satisfied.

Remark 1. Note that the condition (C₃) is a transcendental inequality, which is difficult to solve. The sufficient conditions in Lemma 1 avoid this difficulty. Since the spectral radius of a matrix is always less than or equal to any induced norm of the matrix, Lemma 1 remains valid under the conditions (C₁) and

( ${C^{\prime }}_{\text{2}}$ ) $\underset{Re\left(s\right)\ge 0}{\sup }\Vert k\left(s\right)\Vert <\frac{1}{2}\text{.}$

Now sufficient conditions for asymptotic stability of system (1) are given in the following theorem.

Theorem 2. If the family of matrices $\left\{A,B,C\right\}$ defined in (LFNDDE) satisfies the conditions (C₁) and (C₂), then the system (1) is asymptotically stable for all values of the delay $\tau$.

Proof. By Lemma 1, if the conditions (C₁) and (C₂) are satisfied, then the condition (C₃) holds. This implies that $Re\left(s\right)<0$ for any root of the characteristic equation (4). We need to prove that the roots remain bound away from the imaginary axis. Suppose the contrary. Then there exists a sequence of roots ( $s_m$ ) of the characteristic equation where $Re\left(s_m\right)<0$ and $Re\left(s_m\right)\to 0$ as $m\to \infty$. As in the proof of Lemma 1, we use the notation

$\begin{array}{l}\gamma \left(s\right)={\left(s\left(1-\alpha \right)+\alpha \right)}^{-1},\\ K\left(s\right)={\left(s\gamma \left(s\right)\left(I-C\right)-\left(A+B\right)\right)}^{-1}\left(B+s\gamma \left(s\right)C\right).\end{array}$

Since any eigenvalue ${\lambda }_j\left[K\left(s\right)\left({\text{e}}^{-s\tau }-1\right)\right]$ is a continuous function of s for $Re\left(s\right)\ge 0$, similar to [25] and from the condition (C₂), there exists $\epsilon >0$ such that

$\underset{Re\left(s\right)\ge 0}{\sup }\rho \left[K\left(s\right)\left({\text{e}}^{-s\tau }-1\right)\right]=\underset{Re\left(s\right)\ge 0}{\sup }\underset{j}{\max }\left|{\lambda }_j\left[K\left(s\right)\left({\text{e}}^{-s\tau }-1\right)\right]\right|=1-\epsilon \text{.}$

Hence,

$\underset{Re\left(\omega \right)=0}{\sup }\rho \left[K\left(\omega \right)\left({\text{e}}^{-\omega \tau }-1\right)\right]\le 1-\epsilon \text{.}$ (5)

For sufficiently large m there exists a positive constant ${\epsilon }^{\text{*}}$ ( $0<{\epsilon }^{\text{*}}<\epsilon$ ) and a characteristic root $s_m$ such that $\left|Re\left(s_m\right)\right|$ is sufficiently small, $Re\left(s_m\right)<0$ and

$\left|{\max }_j\left|{\lambda }_j\left[K\left(s_m\right)\left({\text{e}}^{-s_m\tau }-1\right)\right]\right|-\underset{Re\left(\omega \right)=0}{\sup }\rho \left[K\left(\omega \right)\left({\text{e}}^{-\omega \tau }-1\right)\right]\right|<{\epsilon }^{*}.$ (6)

Then it follows from (5) and (6) that for large m and for $j=1,2,\cdots ,n$

$\left|{\lambda }_j\left[K\left(s_m\right)\left({\text{e}}^{-s_m\tau }-1\right)\right]\right|\le \underset{Re\left(\omega \right)=0}{\sup }\rho \left[K\left(\omega \right)\left({\text{e}}^{-\omega \tau }-1\right)\right]+{\epsilon }^{*}<1-\epsilon +{\epsilon }^{*}<1.$

That is, for $Re\left(s_m\right)<0$ and $Re\left(s_m\right)\to 0$ as $m\to \infty$ we obtain $Q\left(s_m,\tau \right)\ne 0$, which contradicts the assumption that ( $s_m$ ) is a sequence of roots of the characteristic equation.

Lemma 2. Let $\left\{A,B,C\right\}$ be the family of matrices defined in (LFNDDE) and satisfying (C₁). Assume that $\left(I-C\right)-\left(A+B\right)$ is nonsingular and define the matrices

$F={\left(\left(I-C\right)-\left(A+B\right)\right)}^{-1}\left(B+C\right),$

$G={\left(\left(I-C\right)-\left(A+B\right)\right)}^{-1}\left(B-C\right),$

$J={\left(\left(I-C\right)-\left(A+B\right)\right)}^{-1}\left(\left(I-C\right)+\left(A+B\right)\right)$.

If

$s{\left(s\left(1-\alpha \right)+\alpha \right)}^{-1}=\frac{1-z}{1+z}$ for $Re\left(s\right)\ge 0$ and $\left|z\right|\le 1$, (7)

then the following equality holds for $Re\left(s\right)\ge 0$ and $\left|z\right|\le 1$

$\begin{array}{l}{\left(s{\left(s\left(1-\alpha \right)+\alpha \right)}^{-1}\left(I-C\right)-\left(A+B\right)\right)}^{-1}\left(B+s{\left(s\left(1-\alpha \right)+\alpha \right)}^{-1}C\right)\\ ={\left(I-zJ\right)}^{-1}\left(F+zG\right).\end{array}$ (8)

Proof. Note first that there is a z satisfying (7). Indeed such a z is given by $z=\frac{\alpha \left(1-s\right)}{2s+\alpha \left(1-s\right)}$ and since $Re\left(s\right)\ge 0$ and $0<\alpha <1$, it is easy to check that $\left|z\right|\le 1$.

A simple algebraic manipulation yields

$\begin{array}{l}I-zJ=I-\frac{\alpha \left(1-s\right)}{2s+\alpha \left(1-s\right)}{\left(\left(I-C\right)-\left(A+B\right)\right)}^{-1}\left(\left(I-C\right)+\left(A+B\right)\right)\\ =2{\left(\left(I-C\right)-\left(A+B\right)\right)}^{-1}\left[\left(s\gamma \left(s\right)\left(I-C\right)-\left(A+B\right)\right)\gamma {\left(s\right)}^{-1}\right]{\left(2s+\alpha \left(1-s\right)\right)}^{-1},\end{array}$

where $\gamma \left(s\right)={\left(s\left(1-\alpha \right)+\alpha \right)}^{-1}$. Note that the condition (C₁) ensures that $I-zJ$ is nonsingular.

Likewise, we have

$\begin{array}{c}F+zG={\left(\left(I-C\right)-\left(A+B\right)\right)}^{-1}\left(B+C+\frac{\alpha \left(1-s\right)}{2s+\alpha \left(1-s\right)}\left(B-C\right)\right)\\ =2{\left(\left(I-C\right)-\left(A+B\right)\right)}^{-1}\left(B+s\gamma \left(s\right)C\right)\gamma {\left(s\right)}^{-1}{\left(2s+\alpha \left(1-s\right)\right)}^{-1}\text{.}\end{array}$

Combining the expressions of $I-zJ$ and $F+zG$ above leads to the desired result.

In view of Theorem 2 and Lemma 2, we obtain the following

Theorem 3. If the family of matrices $\left\{A,B,C\right\}$ defined in (LFNDDE) satisties the assumptions (C₁) and

( ${C^{″}}_{\text{2}}$ ) ${\sup }_{\left|z\right|\le 1}\rho \left[{\left(I-zJ\right)}^{-1}\left(F+zG\right)\right]<\frac{1}{2}$,

where the matrices F, G and J are defined in Lemma 2, then the system (1) is asymptotically stable for all values of the delay $\tau$.

Remark 2. Note that Theorem 3 remains valid if the condition for ( ${C^{″}}_{\text{2}}$ ) is replaced by

( ${C^{‴}}_{\text{2}}$ ) ${\sup }_{\left|z\right|\le 1}\Vert {\left(I-zJ\right)}^{-1}\left(F+zG\right)\Vert <\frac{1}{2}$.

In the following, we give other sufficient conditions ensuring asymptotic stability. For this purpose, we need the following lemma whose proof can be found, for example, in [26].

Lemma 3. For $B\in C^{n\times n},\tau \ge 0$, and $Re\left(s\right)\ge 0$,

$\mu \left(B{\text{e}}^{-s\tau }\right)\le \sqrt{{\rho }^2\left(B_h\right)+{\rho }^2\left(B_k\right)}$,

where $B_h=\frac{1}{2}\left(B+B^{\text{*}}\right),B_k=\frac{i}{2}\left(B-B^{\text{*}}\right)$ and $i^2=-1$.

Theorem 4. If the family of matrices $\left\{A,B,C\right\}$ defined in (LFNDDE) satisfies the following conditions

(H₁) $\Vert C\Vert +\left(1-\alpha \right)\left(\Vert A\Vert +\Vert B\Vert \right)<1,$

(H₂) $\mu \left(A\right)+\sqrt{{\rho }^2\left(B_h\right)+{\rho }^2\left(B_k\right)}+\frac{\Vert CA+CB\Vert +\left(1-\alpha \right)\left[\Vert A^2\Vert +\Vert AB+BA\Vert +\Vert B^2\Vert \right]}{1-\left[\Vert C\Vert +\left(1-\alpha \right)\left(\Vert A\Vert +\Vert B\Vert \right)\right]}<0,$

where $B_h$ and $B_k$ are defined in Lemma 3, then system (1) is asymptotically stable for all values of the delay $\tau$.

Proof. First, we show that the characteristic equation (4) has no roots on the closed right half plane. Let s with $Re\left(s\right)\ge 0$ and $R\left(s\right)=I-\left(C{\text{e}}^{-s\tau }+\left(1-\alpha \right)\left(A+B{\text{e}}^{-s\tau }\right)\right)$. Since

$\begin{array}{l}\rho \left[C{\text{e}}^{-s\tau }+\left(1-\alpha \right)\left(A+B{\text{e}}^{-s\tau }\right)\right]\\ \le \Vert C{\text{e}}^{-s\tau }+\left(1-\alpha \right)\left(A+B{\text{e}}^{-s\tau }\right)\Vert \le \Vert C\Vert +\left(1-\alpha \right)\left(\Vert A\Vert +\Vert B\Vert \right)<1\end{array}$

by condition (H₁), we deduce that $R\left(s\right)$ is nonsingular for all s with $Re\left(s\right)\ge 0$ and

$\Vert R{\left(s\right)}^{-1}\Vert \le \frac{1}{1-\left[\Vert C\Vert +\left(1-\alpha \right)\left(\Vert A\Vert +\Vert B\Vert \right)\right]}\text{.}$ (9)

Let

$s\left(I-C{\text{e}}^{-s\tau }-\left(1-\alpha \right)\left(A+B{\text{e}}^{-s\tau }\right)\right)-\alpha \left(A+B{\text{e}}^{-s\tau }\right)=R\left(s\right)T\left(s\right),$

where

$T\left(s\right)=sI-\alpha M\left(s\right),M\left(s\right)=R{\left(s\right)}^{-1}\left(A+B{\text{e}}^{-s\tau }\right)\text{.}$

The eigenvalues of $T\left(s\right)$ and $T\left(s\right)$ are related by

${\lambda }_j\left[T\left(s\right)\right]=s-\alpha {\lambda }_j\left[M\left(s\right)\right],j=1,\cdots ,n\text{.}$ (10)

Using the formula $R{\left(s\right)}^{-1}=I+R{\left(s\right)}^{-1}\left(I-R\left(s\right)\right)$, the inequality (9), the properties of the logarithmic norm mentioned at the end of Section 2, and Lemma 3, we obtain for all s with $Re\left(s\right)\ge 0$

$\begin{array}{c}Re\left({\lambda }_j\left[M\left(s\right)\right]\right)=Re\left({\lambda }_j\left[A+B{\text{e}}^{-s\tau }+R{\left(s\right)}^{-1}\left(I-R\left(s\right)\right)\left(A+B{\text{e}}^{-s\tau }\right)\right]\right)\\ \le \mu \left(A\right)+\sqrt{{\rho }^2\left(B_h\right)+{\rho }^2\left(B_k\right)}+\Vert R{\left(s\right)}^{-1}\left(I-R\left(s\right)\right)\left(A+B{\text{e}}^{-s\tau }\right)\Vert \end{array}$

and

$\begin{array}{l}\Vert R{\left(s\right)}^{-1}\left(I-R\left(s\right)\right)\left(A+B{\text{e}}^{-s\tau }\right)\Vert \\ \le \Vert R{\left(s\right)}^{-1}\Vert \Vert \left(I-R\left(s\right)\right)\left(A+B{\text{e}}^{-s\tau }\right)\Vert \\ \le \frac{\Vert CA+CB\Vert +\left(1-\alpha \right)\left[\Vert A^2\Vert +\Vert AB+BA\Vert +\Vert B^2\Vert \right]}{1-\left[\Vert C\Vert +\left(1-\alpha \right)\left(\Vert A\Vert +\Vert B\Vert \right)\right]}\text{.}\end{array}$

Therefore from the condition (H₂) it follows that

${\sup }_{Re\left(s\right)\ge 0}{\max }_{j}Re\left({\lambda }_j\left[M\left(s\right)\right]\right)<0.$ (11)

In particular, (10) and (11) show that $T\left(s\right)$ is nonsingular and therefore the roots of the characteristic Equation (4) belong to the open left half of the complex plane. The roots remain uniformly bounded away from the imaginary axis since otherwise for $\epsilon >0$ sufficiently small (so that $0<\epsilon <-\underset{Re\left(s\right)\ge 0}{\sup }{\max }_{1\le j\le n}Re\left({\lambda }_j\left[M\left(s\right)\right]\right)$ ), there would exist a sequence $s_m$ of roots such that for large m, $Re\left(s_m\right)\to 0$ and

$\left|{\max }_{1\le j\le n}Re\left({\lambda }_j\left[M\left(s_m\right)\right]\right)-\underset{Re\left(\omega \right)=0}{\sup }{\max }_{1\le j\le n}Re\left({\lambda }_j\left[M\left(\omega \right)\right]\right)\right|\le \epsilon \text{.}$

But then

$\begin{array}{l}\underset{1\le j\le n}{\max }Re\left({\lambda }_j\left[M\left(s_m\right)\right]\right)\\ =\left(\underset{1\le j\le n}{\max }Re\left({\lambda }_j\left[M\left(s_m\right)\right]\right)-\underset{Re\left(\omega \right)=0}{\sup }\underset{1\le j\le n}{\max }Re\left({\lambda }_j\left[M\left(\omega \right)\right]\right)\right)\\ +\underset{Re\left(\omega \right)=0}{\sup }{\max }_{1\le j\le n}Re\left({\lambda }_j\left[M\left(\omega \right)\right]\right)\\ \le \epsilon +\underset{Re\left(\omega \right)=0}{\sup }{\max }_{1\le j\le n}Re\left({\lambda }_j\left[M\left(\omega \right)\right]\right)<0,\end{array}$

contradicting the assumption that ( $s_m$ ) is a sequence of roots of the characteristic equation.

Now we consider the stability of system (1) in the case (ILFNDDE). From (2) we have

$A^{\left(1\right)}\le A\le A^{\left(2\right)},B^{\left(1\right)}\le B\le B^{\left(2\right)},C^{\left(1\right)}\le C\le C^{\left(2\right)},$

where

$A^{\left(k\right)}={\left[a_{ij}^{\left(k\right)}\right]}_{1\le i,j\le n},B^{\left(k\right)}={\left[b_{ij}^{\left(k\right)}\right]}_{1\le i,j\le n},C^{\left(k\right)}={\left[c_{ij}^{\left(k\right)}\right]}_{1\le i,j\le n},k=1,2.$

Let

$\hat{A}=\frac{1}{2}\left(A^{\left(1\right)}+A^{\left(2\right)}\right),\Delta A=A-\hat{A},A_M=A^{\left(2\right)}-\hat{A},$ (12a)

$\hat{B}=\frac{1}{2}\left(B^{\left(1\right)}+B^{\left(2\right)}\right),\Delta B=B-\hat{B},B_M=B^{\left(2\right)}-\hat{B},$ (12b)

$\hat{C}=\frac{1}{2}\left(C^{\left(1\right)}+C^{\left(2\right)}\right),\Delta C=C-\hat{C},C_M=C^{\left(2\right)}-\hat{C}\text{.}$ (12c)

Then it is easy to see that

$\left|\Delta A\right|\le A_M,\left|\Delta B\right|\le B_M,\left|\Delta C\right|\le C_M\text{.}$ (13)

The following theorem gives sufficient conditions for the stability of (ILFNDDE).

Theorem 5. If the family of matrices $\left\{A,B,C\right\}$ defined in (ILFNDDE) satisfies the following conditions

(P₁) $\rho \left(C_M+\left|\hat{C}\right|\right)<1$,

(P₂) $\det \left[s{\left(s\left(1-\alpha \right)+\alpha \right)}^{-1}I-\left(\hat{A}+\hat{B}\right)\right]\ne 0$, for $Re\left(s\right)\ge 0$,

(P₃) $\underset{Re\left(s\right)\ge 0}{\sup }\rho \left[\left|{\left(s{\left(s\left(1-\alpha \right)+\alpha \right)}^{-1}I-\left(\hat{A}+\hat{B}\right)\right)}^{-1}\right|K\right]<1$,

where

$\begin{array}{c}K={\left(I-\left(C_M+\left|\hat{C}\right|\right)\right)}^{-1}(\left|\hat{C}\hat{A}\right|+3\left|\hat{C}\hat{B}\right|+\left|\hat{C}\right|\left(3B_M+A_M\right)\\ +C_M\left(\left|\hat{A}\right|+A_M+3\left(\left|\hat{B}\right|+B_M\right)\right))+A_M+3B_M+2\left|\hat{B}\right|\end{array}$

then system (1) is asymptotically stable for all values of the delay $\tau$.

Proof. As in the proof of Theorems 2 and 4, we first show that the characteristic Equation (4) has no roots on the closed right half plane. Let s with $Re\left(s\right)\ge 0$. Since

$\rho \left(C{\text{e}}^{-s\tau }\right)\le \rho \left(\left|\left(\Delta C+\hat{C}\right){\text{e}}^{-s\tau }\right|\right)\le \rho \left(\left|\Delta C\right|+\left|\hat{C}\right|\right)\le \rho \left(C_M+\left|\hat{C}\right|\right)<1$

by condition (P₁), we deduce that $I-C{\text{e}}^{-s\tau }$ is nonsingular for all s with $Re\left(s\right)\ge 0$ and

$\left|{\left(I-C{\text{e}}^{-s\tau }\right)}^{-1}\right|\le {\left(I-\left(C_M+\left|\hat{C}\right|\right)\right)}^{-1}\text{.}$ (14)

It is straightforward to verify that

$s\left(I-C{\text{e}}^{-s\tau }-\left(1-\alpha \right)\left(A+B{\text{e}}^{-s\tau }\right)\right)-\alpha \left(A+B{\text{e}}^{-s\tau }\right)=\left(I-C{\text{e}}^{-s\tau }\right)T\left(s\right),$

where

$\begin{array}{l}T\left(s\right)=\left(s\gamma \left(s\right)I-{\left(I-C{\text{e}}^{-s\tau }\right)}^{-1}\left(A+B{\text{e}}^{-s\tau }\right)\right)\gamma {\left(s\right)}^{-1},\\ \gamma \left(s\right)={\left(s\left(1-\alpha \right)+\alpha \right)}^{-1},\end{array}$

and that

$T\left(s\right)=R_1\left(s\right)\left(I-R_2\left(s\right)\right)\gamma {\left(s\right)}^{-1},$

where

$R_1\left(s\right)=s\gamma \left(s\right)I-\left(\hat{A}+\hat{B}\right),$

$\begin{array}{c}{R}_2\left(s\right)=R_1{\left(s\right)}^{-1}\left[\Delta A+\Delta B+B\left({\text{e}}^{-s\tau }-1\right)\right]\\ +R_1{\left(s\right)}^{-1}{\left(I-C{\text{e}}^{-s\tau }\right)}^{-1}C{\text{e}}^{-s\tau }\left[\hat{A}+\hat{B}+\Delta A+\Delta B+B\left({\text{e}}^{-s\tau }-1\right)\right]\text{.}\end{array}$

The condition (P₂) says that $R_1\left(s\right)$ is nonsingular. From (12), (13) and (14) we obtain

$\left|R_2\left(s\right)\right|\le \left|R_1{\left(s\right)}^{-1}\right|\left[A_M+3B_M+2\left|\hat{B}\right|+{\left(I-\left(C_M+\left|\hat{C}\right|\right)\right)}^{-1}{\hat{R}}_M\right],$

where

${\hat{R}}_M=\left|\hat{C}\hat{A}\right|+3\left|\hat{C}\hat{B}\right|+\left|\hat{C}\right|\left(3B_M+A_M\right)+C_M\left(\left|\hat{A}\right|+A_M+3\left(\left|\hat{B}\right|+B_M\right)\right)\text{.}$

It follows from the condition (P₃) that $\rho \left(R_2\left(s\right)\right)<1$ and hence $I-R_2\left(s\right)$ and $T\left(s\right)$ are nonsingular. Thus, the roots of the characteristic equation (4) belong to the open left half of the complex plane. The proof that the roots remain bounded away from the imaginary axis is a simple repetition of the proof of Theorem 2.

4. Numerical Examples

Example 1. Consider a system (LFNDDE) with $\alpha =0.97$ and the matrices

$\begin{array}{l}A=\left(\begin{array}{ccc}-10.00& 0.27& 0.52\\ 0.59& -10.00& 0.58\\ 0.45& 0.09& -10.00\end{array}\right),\\ B=\left(\begin{array}{ccc}0.21& 0.29& 0.41\\ 0.32& 0.81& 0.17\\ 0.40& 0.62& 0.61\end{array}\right),C=\left(\begin{array}{ccc}0.03& 0.01& 0.02\\ 0.01& 0.02& 0.01\\ 0.00& 0.02& 0.01\end{array}\right).\end{array}$

A simple calculation shows that

$\Vert C\Vert +\left(1-\alpha \right)\left(\Vert A\Vert +\Vert B\Vert \right)=0.4<1,$

$\begin{array}{l}\mu \left(A\right)+\sqrt{{\rho }^2\left(B_h\right)+{\rho }^2\left(B_k\right)}+\frac{\Vert CA+CB\Vert +\left(1-\alpha \right)\left[\Vert A^2\Vert +\Vert AB+BA\Vert +\Vert B^2\Vert \right]}{1-\left[\Vert C\Vert +\left(1-\alpha \right)\left(\Vert A\Vert +\Vert B\Vert \right)\right]}\\ =-0.41<0.\end{array}$

We deduce form Theorem 4 that the system is asymptotically stable.

Example 2. Consider a system (ILFNDDE) with $\alpha =0.5$ and the matrices

$A^{\left(1\right)}=\left(\begin{array}{cc}-1.2& 0\\ 0& -1.3\end{array}\right),A^{\left(2\right)}=\left(\begin{array}{cc}-0.8& 0\\ 0& -0.7\end{array}\right),$

$B^{\left(1\right)}=\left(\begin{array}{cc}0& 0.6\\ 0& 0\end{array}\right),B^{\left(2\right)}=\left(\begin{array}{cc}0& 1.4\\ 0& 0\end{array}\right),$

$C^{\left(1\right)}=\left(\begin{array}{cc}0.1& 0\\ 0& 0.1\end{array}\right),C^{\left(2\right)}=\left(\begin{array}{cc}0.2& 0\\ 0& 0.3\end{array}\right)\text{.}$

Then

$\hat{A}=\left(\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right),A_M=\left(\begin{array}{cc}0.2& 0\\ 0& 0.3\end{array}\right),\hat{B}=\left(\begin{array}{cc}0& 1\\ 0& 0\end{array}\right),B_M=\left(\begin{array}{cc}0& 0.4\\ 0& 0\end{array}\right),$

$\hat{C}=\left(\begin{array}{cc}0.15& 0\\ 0& 0.2\end{array}\right),C_M=\left(\begin{array}{cc}0.05& 0\\ 0& 0.1\end{array}\right)\text{.}$

We verify that

· The eigenvalues of $C_M+\left|\hat{C}\right|$ are equal to 0.2 and 0.3. Hence, the condition (P₁) is satisfied.

· The equation $\det \left[\frac{2s}{s+1}I-\left(\hat{A}+\hat{B}\right)\right]=0$ has the unique solution $s=-1/3$. Hence, the condition (P₂) is satisfied. So that ${\left(\frac{2s}{s+1}I-\left(\hat{A}+\hat{B}\right)\right)}^{-1}$ exists and

${\left(\frac{2s}{s+1}I-\left(\hat{A}+\hat{B}\right)\right)}^{-1}=\left(\begin{array}{cc}\left|\frac{s+1}{3s+1}\right|& {\left|\frac{s+1}{3s+1}\right|}^2\\ 0& \left|\frac{s+1}{3s+1}\right|\end{array}\right)$,

$\left|{\left(\frac{2s}{s+1}I-\left(\hat{A}+\hat{B}\right)\right)}^{-1}\right|=\left(\begin{array}{cc}1& 1\\ 0& 1\end{array}\right)$,

where $\left|{\left(\frac{2s}{s+1}I-\left(\hat{A}+\hat{B}\right)\right)}^{-1}\right|$ is a matrix formed by taking maximum magnitude of each element of ${\left(\frac{2s}{s+1}I-\left(\hat{A}+\hat{B}\right)\right)}^{-1}$ for $Re\left(s\right)\ge 0$.

· For condition (P₃), The matrix K is given by

$\begin{array}{c}K={\left(I-\left(C_M+\left|\hat{C}\right|\right)\right)}^{-1}(\left|\hat{C}\hat{A}\right|+3\left|\hat{C}\hat{B}\right|+\left|\hat{C}\right|\left(3B_M+A_M\right)\\ +C_M\left(\left|\hat{A}\right|+A_M+3\left(\left|\hat{B}\right|+B_M\right)\right))+A_M+3B_M+2\left|\hat{B}\right|\end{array}$

We have

$A_M+3B_M+2\left|\hat{B}\right|=\left(\begin{array}{cc}0.2& 3.2\\ 0& 0.3\end{array}\right)$

${\left(I-\left(C_M+\left|\hat{C}\right|\right)\right)}^{-1}=\left(\begin{array}{cc}1.25& 0\\ 0& 1.4285\end{array}\right)$

$\left|\hat{C}\hat{A}\right|=\left(\begin{array}{cc}0.15& 0\\ 0& 0.2\end{array}\right)$

$3\left|\hat{C}\hat{B}\right|=\left(\begin{array}{cc}0& 0.45\\ 0& 0\end{array}\right)$

$\left|\hat{C}\right|\left(3B_M+A_M\right)=\left(\begin{array}{cc}0.03& 0.18\\ 0& 0.06\end{array}\right)$

$C_M\left(\left|\hat{A}\right|+A_M+3\left(\left|\hat{B}\right|+B_M\right)\right)=\left(\begin{array}{cc}0.06& 0.21\\ 0& 0.13\end{array}\right)$

So that $K=\left(\begin{array}{cc}0.5& 4.25\\ 0& 0.85\end{array}\right)$. For $Re\left(s\right)\ge 0$ we have

$\left|{\left(\frac{2s}{s+1}I-\left(\hat{A}+\hat{B}\right)\right)}^{-1}\right|K=\left(\begin{array}{cc}0.5& 5.1\\ 0& 0.85\end{array}\right)$

and the eigenvalues of $\left|{\left(\frac{2s}{s+1}I-\left(\hat{A}+\hat{B}\right)\right)}^{-1}\right|K$ are equal to 0.5 and 0.85. Hence

$\rho \left[\left|{\left(\frac{2s}{s+1}I-\left(\hat{A}+\hat{B}\right)\right)}^{-1}\right|K\right]<1.$

We deduce form Theorem 5 that the system is asymptotically stable.

5. Conclusion

This paper is concerned with the asymptotic stability of linear fractional-order neutral differential delay systems described by the Caputo-Fabrizio derivative. The systems matrices can be constant or interval matrices. Using the Laplace transform, we have derived a new characteristic equation for such systems. This characteristic equation, though interesting in theory, involves a transcendental term which makes it difficult to use in practice and in particular to study the asymptotic stability of such systems. To overcome this difficulty, sufficient algebraic criteria have been given to ensure the asymptotic stability of such systems in the case of constant matrices (Lemma 1 and Lemma 2). We have successfully shown that under these algebraic criteria, asymptotic stability holds (Theorem 2 and Theorem 3). Also, norm-based criteria have been given to ensure the asymptotic stability. In particular, in case of constant matrices, Theorem 4 involves easily verifiable criteria based only on matrix norm computations. Finally, sufficient conditions are derived to ensure the asymptotic stability of such systems in the case of interval matrices. We have shown that this system is asymptotically stable for any delay parameter (Theorem 5). The effectiveness of the theoretical results has been illustrated by numerical examples.

Acknowledgements

The authors are grateful to the anonymous referees for their constructive comments and suggestions, improving this paper greatly.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Goularta, A.G.O., Lazoa, M.J., Suareza, J.M.S. and Moreirab, D.M. (2017) Fractional Derivative Models for Atmospheric Dispersion of Pollutants. Physica A: Statistical Mechanics and Its Applications, 477, 9-19. https://doi.org/10.1016/j.physa.2017.02.022
[2]	Sierociuka, D., Skovranekb, T., Maciasa, M., Podlubnyb, I., Petrasb, I., Dzielinskia, A. and Ziubinski, P. (2015) Diffusion Process Modeling by Using Fractional-Order Models. Applied Mathematics and Computation, 257, 2-11. https://doi.org/10.1016/j.amc.2014.11.028
[3]	Atangana, A. and Baleanu, D. (2017) Application of Fixed Point Theorem for Stability Analysis of a Nonlinear Schrodinger with Caputo-Liouville Derivative. Filomat, 31, 2243-2248. https://doi.org/10.2298/FIL1708243A
[4]	Kaslik, E. and Sivasundaram, S. (2012) Analytical and Numerical Methods for the Stability Analysis of Linear Fractional Delay Differential Equations. Journal of Computational and Applied Mathematics, 236, 4027-4041. https://doi.org/10.1016/j.cam.2012.03.010
[5]	Li, H., Zhong, S. and Li, H. (2015) Asymptotic Stability Analysis of a Fractional-Order Neutral Systems with Time Delay. Advances in Difference Equations, 2015, Article No. 325. https://doi.org/10.1186/s13662-015-0659-4
[6]	Podlubny, I. (1999) Fractional Differential Equations. Vol. 198 of Mathematics in Science and Engineering. Technical University of Kosice, Kosice.
[7]	Caputo, M. and Fabrizio, M. (2015) A New Definition of Fractional Derivative without Singular Kernel. Progress in Fractional Differentiation and Applications, 1, 73-85.
[8]	Liu, K., Feckan, M., Regan, D. and Wang, J. (2019) Hyers-Ulam Stability and Existence of Solutions for Differential Equations with Caputo-Fabriziofractional Derivative. Mathematics, 7, 333. https://doi.org/10.3390/math7040333
[9]	Atanackovic, T.M., Pilipovic, S. and Zorica, D. (2018) Properties of the Caputo-Fabrizio Fractional Derivative and Its Distributional Settings. Fractional Calculus and Applied Analysis, 21, 24-29. https://doi.org/10.1515/fca-2018-0003
[10]	Baleanu, D., Mousalou, A. and Rezapoor, S. (2018) The Extended Fractional Caputo-Fabrizio Derivative of Order 2 < σ < 1 on CR [0, 1] and the Existence of Solutions for Two Higher-Order Series-Type Differential Equations. Advances in Difference Equations, 2018, Article No. 255.
[11]	Caputo, M. and Fabrizio, M. (2018) Applications of New Time and Spatial Fractional Derivatives with Exponential Kernels. Progress in Fractional Differentiation and Applications, 2, 1-11.
[12]	Dassios, I. and Baleanu, D. (2018) Caputo and Related Fractional Derivatives in Singular Systems. Applied Mathematics and Computation, 337, 591-606. https://doi.org/10.1016/j.amc.2018.05.005
[13]	Kaczorek, T. (2015) Reachability of Fractional Continuous-Time Linear Systems Using the Caputo-Fabrizio Derivagtive. In: Claus, T., Herrmann, F., Manitz, M. and Rose, O., Eds., Proceeding 30th European Conference on Modelling and Simulation.
[14]	Li, K., Lu, S. and Xu, T. (2019) A Fully Discrete Spectral Method for Fractional Cattaneo Equation Based on Caputo-Fabrizio Derivative. Numerical Methods for Partial Differential Equations, 35, 936-954. https://doi.org/10.1002/num.22332
[15]	Qureshi, S., Norodin, R. and Baleanu, D. (2019) New Numerical Aspects of Caputo-Fabrizio Fractional Derivative Operator. Mathematics, 7, 374. https://doi.org/10.3390/math7040374
[16]	Pang, D. and Jiang, W. (2014) Finite-Time Stability Analysis of Fractional Singular Time-Delay Systems. Advances in Difference Equations, 2014, Article No. 259. https://doi.org/10.1186/1687-1847-2014-259
[17]	Li, H., Cheng, J., Li, H. and Zhong, S. (2019) Stability Analysis of a Fractional-Order Linear System Described by the Caputo-Fabrizio Derivative. Mathematics, 7, 200. https://doi.org/10.3390/math7020200
[18]	Li, H., Zhong, S., Cheng, J. and Li, H. (2019) Stability Analysis of a Fractional-Order Linear System with Time Delay Described by the Caputo-Fabrizio Derivative. Advances in Difference Equations, 2019, Article No. 86. https://doi.org/10.1186/s13662-019-2024-5
[19]	Yuhong, H. and Jia-Bao, L. (2019) Robust H1 Control for Uncertain Singular Neutral Time-Delay Systems. Mathematics, 7, 217. https://doi.org/10.3390/math7030217
[20]	Zhong, S., et al. (2017) Stability Analysis of Linear Fractional-Order Neutral Systems with Time Delay. Science Journal of Circuits, Systems and Signal Processing, 6, 1. https://doi.org/10.11648/j.cssp.20170601.11
[21]	Zhong, S., et al. (2014) Stability Analysis of Fractional-Order Systems with Time Delay. International Journal of Mathematical and Computational Sciences, 8, 660.
[22]	Zhong, S., et al. (2012) Stability of Interval Fractional-Order Systems with Order 0 < α < 1. International Journal of Mathematical and Computational Sciences, 6, 987-991.
[23]	Horn, R.A. and Johnson, C.R. (2013) Matrix Analysis. Second Edition, Cambridge University Press, Cambridge.
[24]	Deng, W., Li, C. and Li, J. (2007) Stability Analysis of Linear Fractional Differential System with Multiple Time Delays. Nonlinear Dynamics, 48, Article ID: 409416. https://doi.org/10.1007/s11071-006-9094-0
[25]	Hu, G. and Cahlon, B. (2001) Algebraic Criteria for Stability of Linear Neutral Systems with a Single Delay. Journal of Computational and Applied mathematics, 135, 125-133. https://doi.org/10.1016/S0377-0427(00)00570-7
[26]	Cao, D.Q., He, P. and Zhang, K. (2003) Exponential Stability Criteria of Uncertain Systems with Multiple Time Delays. Journal of Mathematical Analysis and Applications, 283, 362-374.