The Equivalence between Orthogonal Iterations and Alternating Least Squares

Achiya Dax

Hydrological Service, Jerusalem, Israel.

DOI: 10.4236/alamt.2020.102002                

Abstract

This note explores the relations between two different methods. The first one is the Alternating Least Squares (ALS) method for calculating a rank-k approximation of a real m×n matrix, A. This method has important applications in nonnegative matrix factorizations, in matrix completion problems, and in tensor approximations. The second method is called Orthogonal Iterations. Other names of this method are Subspace Iterations, Simultaneous Iterations, and block-Power method. Given a real symmetric matrix, G, this method computes k dominant eigenvectors of G. To see the relation between these methods we assume that G = A^T A. It is shown that in this case the two methods generate the same sequence of subspaces, and the same sequence of low-rank approximations. This equivalence provides new insight into the convergence properties of both methods.

Keywords

Alternating Least Squares (ALS), Orthogonal Iterations, Equivalence Relations, Low-Rank Approximations

1. Introduction

The alternating least squares (ALS) method has several important applications, e.g., [1] - [54]. The origin of the method lies in the field of statistical Principal Components Analysis, e.g., [37] [47] [52] [53]. In the modern era, it is widely used in problems where standard SVD methods are not applicable. These problems include, for example, nonnegative matrix factorization [6] [17] [28] [35] [36], matrix completion problems [5] [14] [15] [20] [23] [24] [30] [54], and tensor approximations [12] [18] [29] [48] [49] [50]. In this note, we consider the ALS method as means for calculating low-rank approximations of large sparse matrices. Let $A\in {ℝ}^{m\times n}$ be a given large sparse matrix, let k be a given integer (the desired matrix rank) which is considerably smaller than $\min \left\{m\mathrm{,}n\right\}$ , and let

${\mathbb{B}}_k=\left\{B\mathrm{<mo>\; |\; </mo>}B\in {ℝ}^{m\times n}\text{and}\text{rank}\left(B\right)\le k\right\}$

denote the set of all the real $m\times n$ matrices whose rank is at most k. Then the term “low-rank approximation” refers to a matrix $B\in {\mathbb{B}}_k$ that approximates A. More precisely, we seek a matrix that solves the problem

$\begin{array}{l}\text{minimize}F\left(B\right)={\Vert A-B\Vert }_F^2\\ \text{subject}\text{to}B\in {\mathbb{B}}_k\mathrm{,}\end{array}$ (1.1)

where ${\Vert \cdot \Vert }_F$ denotes the Frobenius matrix norm. Recall that a rank-k truncated SVD of A provides a solution of (1.1). However, when A is a large sparse matrix, a standard SVD of A can be “too expensive”. This motivates the use of “cheaper” methods which are able to exploit the sparsity of A. The ALS algorithm is aimed at solving the problem

$\begin{array}{l}\text{minimize}F\left(X\mathrm{,}Y\right)={\Vert A-X{Y}^{\text{T}}\Vert }_F^2\\ \text{subject}\text{to}X\in {ℝ}^{m\times k}\text{and}Y\in {ℝ}^{n\times k}\mathrm{.}\end{array}$ (1.2)

Note that (1.1) and (1.2) are equivalent in the sense that a solution of one problem provides a solution to the other problem. The idea behind the ALS algorithm is rather simple. The $\mathcal{l}\text{th}$ iteration, $\mathcal{l}=\mathrm{1,2,}\cdots$ is composed of the following two steps.

Step 1: Given $Y_{\mathcal{l}}\in {ℝ}^{n\times k}$ compute $X_{\mathcal{l}+1}$ to be a solution of the least squares problem

$\begin{array}{l}\text{minimize}f\left(X\right)={\Vert A-X{Y}_{\mathcal{l}}^{\text{T}}\Vert }_F^2\\ \text{subject}\text{to}X\in {ℝ}^{m\times k}\mathrm{.}\end{array}$ (1.3)

Step 2: Given $X_{\mathcal{l}+1}\in {ℝ}^{m\times k}$ , compute $Y_{\mathcal{l}+1}$ to be a solution of the least squares problem

$\begin{array}{l}\text{minimize}g\left(Y\right)={\Vert A-X_{\mathcal{l}+1}{Y}^{\text{T}}\Vert }_F^2\\ \text{subject}\text{to}Y\in {ℝ}^{n\times k}\mathrm{.}\end{array}$ (1.4)

The details of the ALS iteration are discussed in the next section.

The orthogonal iterations method has different aim and different motivation. Let $G\in {ℝ}^{n\times n}$ be a given symmetric matrix. Then this method is aimed at computing k dominant eigenvectors of G. It is best suited for handling large sparse matrices in which a matrix-vector product needs only $0\left(n\right)$ flops. It is also assumed that k is considerably smaller than n. Other names of this method are “subspace iterations”, “simultaneous iterations” and “block-Power method”, e.g., [3] [4] [11] [16] [19] [39] [40] [41] [42] [44] [46]. The idea behind this method is to use a block version of the Power method that includes frequent orthogonalizations. The $\mathcal{l}\text{th}$ iteration, $\mathcal{l}=\mathrm{1,2,}\cdots$ , is composed of the following two steps. It starts with a matrix $V_{\mathcal{l}}\in {ℝ}^{n\times k}$ that has orthonormal columns. The column space of $V_{\mathcal{l}}$ approximates the desired invariant subspace of G.

Step 1: Given $V_{\mathcal{l}}$ , compute the matrix

$W_{\mathcal{l}+1}=G{V}_{\mathcal{l}}\mathrm{.}$ (1.5)

Step 2: Compute $V_{\mathcal{l}+1}$ to be a matrix whose columns constitute an orthonormal basis of $\text{Range}\left(W_{\mathcal{l}+1}\right)$ . In practice $V_{\mathcal{l}+1}$ is obtained by applying a QR factorization of $W_{\mathcal{l}+1}$ .

Using the Rayleigh-Ritz procedure it is possible to extract from $V_{\mathcal{l}+1}$ the corresponding estimates of the desired eigenpairs of G. The details are discussed in Section 3.

The aim of this note is to show that ALS is closely related to “orthogonal iterations”. To see this relation we assume that $G=A^{\text{T}}A$ . In this case the two methods generate the same sequence of subspaces, and the same sequence of low-rank approximations. The proof is given in Section 4.

The equivalence relations that we derive provide important insight into the behavior of both methods. In particular, as explained in Section 3, the rate of convergence of orthogonal iterations is determined by ratios between certain eigenvalues of G. This implies that the rate of convergence of the ALS method obeys a similar rule. Moreover, there are several ways to accelerate orthogonal iterations, and these methods can be adapted to accelerate the ALS method. Conversely, being a minimization method the objective function of the ALS method is monotonic decreasing. This suggests that the orthogonal iterations method has an analogous property.

The relation between ALS and the block-Power method was recently observed by Jain et al. [24] in the context of matrix completion algorithms. A further discussion of this relation is given in Hardt [21] [22]. However, the observations made in these works are using several assumptions on the data matrix. For example, it is assumed that A has missing entries, and that the locations of the missing entries (or the known entries) satisfy certain statistical conditions. It is also assumed that the singular vectors of A satisfy a certain coherence requirement, that A is a low-rank matrix, and in [21] [22] it is assumed to be symmetric. In contrast, our analysis makes no assumption on A. Consequently, the algorithms considered in [21] [22] [24] are quite different from the classic versions that are discussed below, which yield different results. Anyway, an important consequence made in [21] [22] [24] is that the convergence properties of orthogonal iterations can be used to understand the behavior of ALS when applied to matrix completion problems. The equivalence relations that we derive in the next sections help to achieve this goal.

2. The Alternating Least Squares (ALS) Method

In this section we describe two versions of the ALS iteration. The basic scheme solves the linear systems by using a QR factorization that is followed by a back substitution process, while the modified scheme avoids back substitution. This reduces the computational effort per iteration and helps to see the relation with orthogonal iterations.

The first step of the basic iteration requires the solution of (1.3). Let $a_i^{\text{T}}\mathrm{,}i=\mathrm{1,}\cdots \mathrm{,}m$ , denote the ith row of A, and let $x_i^{\text{T}}\mathrm{,}i=\mathrm{1,}\cdots \mathrm{,}m$ , denote the ith row of $X_{\mathcal{l}+1}$ . Then, by comparing $a_i^{\text{T}}$ against $x_i^{\text{T}}{Y}_{\mathcal{l}}^{\text{T}}$ we see that $x_i$ solves the linear least squares problem

$\text{minimize}f\left(x\right)={\Vert Y_{\mathcal{l}}x-a_i\Vert }_2^2\mathrm{,}$ (2.1)

where ${\Vert \cdot \Vert }_2$ denotes the Euclidean vector norm. The solution of (2.1) is carried out by applying a QR factorization of $Y_{\mathcal{l}}$ of the form

$Y_{\mathcal{l}}={\tilde{Q}}_{\mathcal{l}}{\tilde{R}}_{\mathcal{l}}\mathrm{,}$ (2.2)

where ${\tilde{Q}}_{\mathcal{l}}\in {ℝ}^{n\times k}$ , ${\tilde{Q}}_{\mathcal{l}}^{\text{T}}{\tilde{Q}}_{\mathcal{l}}=I$ , and ${\tilde{R}}_{\mathcal{l}}\in {ℝ}^{k\times k}$ is an upper triangular matrix.

Similar arguments enable us to solve (1.4). Let $c_j\mathrm{,}j=\mathrm{1,}\cdots \mathrm{,}n$ , denote the jth column of A, and let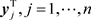, denote the jth row of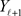. Then by comparing 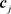against 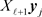we see that 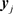solves the linear least squares problem

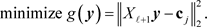(2.3)

The computation of 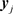is carried out by applying a QR factorization of 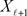that has the form

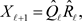(2.4)

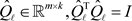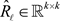where, and is an upper triangular matrix.

Assume for simplicity that the matrices 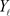and 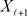have full column rank, which means that and 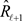are invertible matrices. This enables us to express the solutions of Problem (2.1) and (2.3) as

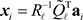(2.5)

and

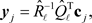(2.6)

respectively. In practice, a matrix-vector product of the form is computed by solving the system via back substitution. In matrix notations the above equalities are summarized as

(2.7)

and

(2.8)

Below we describe a modified scheme which save the multiplications by and. (That is, it avoids the back substitution processes.)

The modified scheme is based on the following observations. Let be any invertible matrix, then

(2.9)

The last equality allows us to replace with, which turns (1.3) into the form

(2.10)

while the last problem has explicit solution,

(2.11)

Similarly, it is possible to replace with, which turns (1.4) into the form

(2.12)

while the last problem has explicit solution,

(2.13)

The modified ALS iteration is summarized in the following two steps.

Step 1: Given compute the QR factorization (2.2) and obtain from (2.11).

Step 2: Given compute the QR factorization (2.4) and obtain from (2.13).

Let, denote the rank-k approximations that are generated by the basic ALS iterations (2.7) - (2.8). Then, in exact arithmetic, the modified scheme generates the same sequence of approximations. Consequently since (2.7) - (2.8) are repeatedly solving (1.3) and (1.4), the sequence, has the decreasing property

(2.14)

Moreover, as we now show, both versions satisfy

(2.15)

Consider first the iteration (2.7) - (2.8). Then combining (2.4) and (2.7) yields

(2.16)

and

(2.17)

while substituting the last expression for into (2.8) gives

(2.18)

Thus, in exact arithmetic (2.15) holds. Similarly, in the modified scheme (2.4) and (2.11) give

(2.19)

while from (2.13) we obtain

(2.20)

In the next sections we shall see that orthogonal iterations share a similar property.

Observe that the modified ALS iteration is not using the matrices and. This feature helps to overcome a possible rank deficiency of or. In classical Gram-Schmidt orthogonalization rank deficiency may cause a gradual loss of orthogonality, but this can be avoided by reorthogonalization and column pivoting, or by using Householder QR with column pivoting. For detailed discussions of the QR factorization see [7] [8] [9] [13] [19] [45]. The modified ALS iteration has recently been considered in Oseledets et al. [38] under the name “simultaneous orthogonal iterations”. It is shown there that the modified version is equivalent to ALS and, therefore, has the same rate of convergence.

3. Orthogonal Iterations

Let be a real symmetric matrix with eigenvalues

(3.1)

Then the orthogonal iterations method is aimed at calculating the k largest eigenvalues of G, , and the corresponding eigenvectors. The iteration, , is composed of the following two steps.

Step 1: Given a matrix, compute a QR factorization of:

(3.2)

Step 2: Compute from the rule

(3.3)

The approximation of the desired eigenpairs is achieved by applying the Rayleigh-Ritz procedure. For this purpose the basic iteration is extended with the following three steps.

Step 3: Compute the related Rayleigh-quotient matrix

(3.4)

Step 4: Compute a spectral decomposition of:

(3.5)

where, and is a diagonal matrix such that

(3.6)

(The diagonal entries of are called “Ritz values”.)

Step 5: If desired compute the related matrix of k “Ritz vectors”,

(3.7)

It is important to note that Steps 3 - 5 are not essential for the computation of. Hence it is possible to defer these steps. The orthogonal iterations method and its convergence properties are derived in the pioneering works of Bauer [4], Jennings [25] [26], Stewart [44], Rutishauser [40] [41], and Clint and Jennings [11]. In these papers the method is called the simultaneous iteration. See also the discussions in ( [3], pp. 54-55), ( [16], pp. 156-159), ( [19], pp. 367-368) and ( [39], pp. 288-299). It is shown there that the computed Ritz values in (3.4) - (3.7) converge toward the corresponding eigenvalues of G. Assume that, then for, the sequence, converges toward, and the asymptotic rate of convergence is determined by the ratio

(3.8)

In other words, the sequence, converges to zero at about the same speed as the sequence. Furthermore, if is a simple eigenvalue then the jth Ritz vector converges toward the jth eigenvector of G and the rate of convergence is determined by the ratio (3.8).

The last observations open the gate for accelerating the basic orthogonal iteration. Below we mention a number of ways to achieve this task.

Increasing the subspace dimension. In this approach the number of columns in the matrix is increased to be where is a small integer. (Typical values of q are k or 2k.) The advantage of this modification is that the convergence ratio changes to

(3.9)

and it can be much smaller than (3.8). The price paid for this gain is that the storage requirements and the computational efforts per iteration are increased. The next acceleration attempts to avoid this penalty.

Power acceleration. In this iteration the updating of in Step 2 is changed to

(3.10)

where is a small integer. The advantage of this modification is that now the convergence ratio is reduced to

(3.11)

Thus one iteration of this kind has the same effect as p iterations of the basic scheme. The main saving is, therefore, a smaller number of orthogonalizations. In practice p is often restricted to stay smaller than 10. The reason lies in the following difficulty. Assume for a moment that. In this case G has a unique dominant eigenvector. Then, as p increases the columns of the matrix tend toward the dominant eigenspace of G, and becomes highly rank-deficient. Other helpful modifications include polynomial acceleration (which is often based on Chebyshev polynomials), and locking (a type of deflation), e.g., [3] and [39].

4. Equivalence Relations

In this section we derive equivalence relations between the ALS method and the orthogonal iterations method. To see these relations we make the assumption that

(4.1)

and use the following notations. Let, denote the sequence of matrices that are generated by the orthogonal iteration method, and let

(4.2)

denote the related QR factorization of. Similarly, let the matrices, , be obtained by the ALS method, and let

(4.3)

denote the related QR factorization of. Then Step 2 of the orthogonal iteration method gives

(4.4)

while from (2.15) we obtain

(4.5)

These equalities lead to the following conclusion.

Theorem 1. Assume that the initial matrices satisfy

(4.6)

Then in exact arithmetic we have

(4.7)

and

(4.8)

for. In other words, the two methods generate the same sequence of subspaces!

Proof. The proof is a direct consequence of (4.4) and (4.5) using induction on. □

We have seen that the matrix solves (2.10). Hence the rank-k approximation of A that corresponds to has the form

(4.9)

Similarly, the rank-k approximation of A that corresponds to has the form

(4.10)

The next theorem shows that these approximations are equal.

Theorem 2 (Rank-k approximations). Using the former assumptions and notations we have the equality

(4.11)

In other words, the two methods generate the same sequence of rank-k approximations.

Proof. Let be some vector in. Then from (4.8) we see that the projection of on Range () equals the projection of on Range (). That is,

(4.12a)

and

(4.12b)

while the last equality implies (4.11).

Corollary 3 (The decreasing property). Recall that the ALS method has the decreasing property (2.14). Now (4.11) implies that this property is also shared by the orthogonal iteration method.

The next lemma helps to convert the decreasing property into an equivalent increasing property.

Lemma 4. Let and be as above. Then

(4.13)

Proof. Let us complete the columns of to be an orthonormal basis of. This gives us an orthonormal matrix

(4.14)

where is an matrix that satisfies

(4.15)

and O denotes a null matrix. Observe that the structure of Z implies the equality

(4.16)

On the other hand, since the Frobenius norm is unitarily invariant,

Corollary 5. Since the sequence is monotonic decreasing, equality (4.13) implies that the sequence is monotonic increasing. That is,

(4.17)

for.

Observe also that

where is the Rayleigh-quotient matrix (3.4), and, are the corresponding Ritz values. This relation leads to the following conclusion, which appears to be a new property of the orthogonal iteration method.

Corollary 6 (A trace increasing property). Let G be a symmetric positive semidefinite matrix and let the matrices, be generated by the orthogonal iterations method. Then

(4.18)

for. □

We have seen in Section 3 that the rate of convergence of the orthogonal iterations method depends on the ratio (3.8). Now the equivalence relations that we have proved suggest that the ALS method behaves in a similar way. To state this result more precisely we need the following notations. Let

(4.19)

denote the singular values of A, and let

(4.20)

denote the singular values of,. Then, clearly,

(4.21)

Similarly, since, the singular values of satisfy

(4.22)

These relations lead to the following observation, which seems to be a new property of the ALS method.

Theorem 7. Assume that, then for, the sequence

(4.23)

converges to zero at the same asymptotic rate as the sequence

(4.24)

Proof. From (4.21) and (4.22) we conclude that the sequence

(4.25)

converges to zero at the same asymptotic rate as the sequence (4.24). Yet, since

(4.26)

the sequence (4.23) shares this property. □

The last theorem implies that the rate of convergence of ALS can be improved by increasing the subspace dimension (See Section 3).

The fact that the two methods converge at the same speed raises the question of which iteration is more efficient to use. One advantage of the orthogonal iterations method is that it stores and updates only (estimates for) the right singular vectors of A. This halves the storage requirements and the number of orthogonalizations. The orthogonal iterations method achieves one QR factorization per iteration, while ALS requires two QR factorizations per iteration. The computation of the left singular vectors and the related low-rank approximation of A is deferred to the end of the iterative process. A further saving can be gained by applying Power acceleration.

However, being a variant of the Block Power method, the orthogonal iteration is expected to be slower than Krylov subspace methods that are based on Lanczos algorithm. See, for example, the comparisons in ( [19], pp. 554-555), ( [39], pp. 250-252), and ( [46], pp. 272-275). Recent Krylov methods are using implicitly restarted Lanczos schemes, e.g., [10] [43] [51], and this approach is considerably faster than orthogonal iterations. Consequently the ALS method is expected to be slower than restarted Krylov methods for low-rank approximations, e.g., [1] [2] [33] [34]. This drawback is, perhaps, the reason that the use of ALS has been moved to problems in which it is difficult to apply a standard SVD algorithm or a restarted Krylov method.

5. Concluding Remarks

As noted in the introduction, the relations between ALS and the block-Power method were recently observed in the context of matrix completion algorithms. However, the related matrix completion algorithms differ substantially from the classic versions discussed in this paper. Indeed, the equivalence between ALS and orthogonal iterations is somewhat surprising, as these methods are well known for many years, and the basic ALS iteration, which uses back-substitutions, is quite different from the orthogonal iteration. The modified version avoids back substitutions, which helps to see the similarity between the two methods.

The equivalence relations bring important insight into the behavior of both methods. One consequence is that the convergence properties of ALS are identical to those of orthogonal iterations. This means that the rate of convergence of the ALS method is determined by the ratios in (4.24), which appears to be a new result. Similarly, the descent property of ALS implies a trace increasing property of the orthogonal iteration method.

The orthogonal iterations method needs less storage requirements, and less QR factorizations per iteration. In addition, it has a number of useful accelerations. These advantages suggest that replacing ALS with orthogonal iterations might be helpful in some applications. On the other hand, the ALS method can be modified to handle problems that other methods cannot handle, such as non-negative matrix factorizations (NMF), matrix completion problems, and tensor decompositions. The ALS iteration that is implemented in these problems is often quite different from the basic iteration (2.7) - (2.8). Yet in some cases it has a similar asymptotic behavior. This happens, for example, in NMF problems when (nearly) all the entries in the converging factors are positive. Another example is the proximal-ALS algorithm in matrix completion, see ( [14], p. 134). In such cases the new results provide important insight into the asymptotic behaviour of the algorithm.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Baglama, J. and Reichel, L. (2005) Augmented Implicitly Restarted Lanczos Bidiagonalization Methods. SIAM Journal on Scientific Computing, 27, 19-42. https://doi.org/10.1137/04060593X
[2]	Baglama, J. and Reichel, L. (2013) An Implicitly Restartedf Block Lanczos Bidiagonalization Method, Using Leja Shifts. BIT Numerical Mathematics, 64, 263-293. https://doi.org/10.1007/s10543-012-0409-x
[3]	Bai, A., Demmel, J., Dongarra, J., Ruhe, A. and van der Vorst, H. (1999) Templates for the Solution of Algebraic Eigenvalue Problems: A Practical Guide. SIAM, Philadelphia, PA. https://doi.org/10.1137/1.9780898719581
[4]	Bauer, F.L. (1957) Das Verfahren der Treppeniteration und verwandte Verfahren zur Lösung algebraischers Eigenwertprobleme. Zeitschrift für angewandte Mathematik und Physik, 8, 214-235. https://doi.org/10.1007/BF01600502
[5]	Bell, R. and Koren, Y. (2007) Scalable Collaborative Filtering with Jointly Derived Neighborhood Interpolation Weights. Proceedings of the 2007 Seventh IEEE International Conference on Data Mining, Omaha, 28-31 October 2007, 43-52. https://doi.org/10.1109/ICDM.2007.90
[6]	Berry, M.W., Browne, M., Langville, A.N., Pauca, V.P. and Plemmons, R.J. (2006) Algorithms and Applications for Approximate Nonnegative Matrix Factorization, 2006. Computational Statistics and Data Analysis. https://doi.org/10.1016/j.csda.2006.11.006
[7]	Bjorck, A. (1967) Solving Linear Least-Squares Problems by Gram-Schmidt Orthogonalization. BIT, 7, 1-21. https://doi.org/10.1007/BF01934122
[8]	Bjorck, A. (1994) Numerics of Gram-Schmidt Orthogonalization. Linear Algebra and Its Applications, 197/198, 297-316. https://doi.org/10.1016/0024-3795(94)90493-6
[9]	Bjorck, A. (1996) Numerical Methods for Least-Squares Problems. SIAM, Philadelphia, PA. https://doi.org/10.1137/1.9781611971484
[10]	Calvetti, D., Reichel, L. and Sorenson, D.C. (1994) An Implicitly Restarted Lanczos Method for Large Symmetric Eigenvalue Problems. Electronic Transactions on Numerical Analysis, 2, 1-21.
[11]	Clint, M. and Jennings, A. (1970) The Evaluation of Eigenvalues and Eigenvectors of Real Symmetric Matrices by Simultaneous Iteration. The Computer Journal, 13, 76-80. https://doi.org/10.1093/comjnl/13.1.76
[12]	Comon, P., Luciani, X. and De Almeida, A.L.F. (2009) Tensor Decompositions, Alternating Least Squares and Other Tales. Journal of Chemometrics, 23, 393-405. https://doi.org/10.1002/cem.1236
[13]	Dax, A. (2000) A Modified Gram-Schmidt Algorithm with Iterative Orthogonalization and Column Pivoting. Linear Algebra and Its Applications, 310, 25-42. https://doi.org/10.1016/S0024-3795(00)00022-7
[14]	Dax, A. (2014) Imputing Missing Entries of a Data Matrix: A Review. Journal of Advanced Computing, 3, 98-222. https://doi.org/10.7726/jac.2014.1007
[15]	Dax, A. (2017) A Gradual Rank Increasing Process for Matrix Completion. Numerical Algorithms, 76, 959-976. https://doi.org/10.1007/s11075-017-0292-2
[16]	Demmel, J.W. (1997) Applied Numerical Linear Algebra. SIAM, Philadelphia, PA. https://doi.org/10.1137/1.9781611971446
[17]	Elden, L. (2007) Matrix Methods in Data Mining and Pattern Recognition. SIAM, Philadelphia, PA. https://doi.org/10.1137/1.9780898718867
[18]	Espig, M. and Khachatryan, A. (2014) Convergence of Alternating Least Squares Optimisation for Rank-One Approximation to High Order Tensors. https://www.igpm.rwth-aachen.de/forschung/preprints/412
[19]	Golub, G.H. and Van Loan, C.F. (2013) Matrix Computations. 4th Edition, Johns Hopkins University, Baltimore.
[20]	Grung, B. and Manne, R. (1998) Missing Values in Principal Component Analysis. Chemometrics and Intelligent Laboratory System, 42, 125-139. https://doi.org/10.1016/S0169-7439(98)00031-8
[21]	Hardt, M. (2013) On the Provable Convergence of Alternating Minimization for Matrix Completion. arXiv. 1312.0925.
[22]	Hardt, M. (2014) Understanding Alternating Minimization for Matrix Completion. Proceedings of the2014 55th Foundations of Computer Science (FOCS), Philadelphia, PA, 18-21 October 2014. https://doi.org/10.1109/FOCS.2014.75
[23]	Hastie, T., Mazumder, R., Lee, J.D. and Zadeh, R. (2015) Matrix Completion and Low-Rank SVD via Fast Alternating Least Squares. Journal of Machine Learning Research, 16, 3367-3402.
[24]	Jain, P., Netrapalli, P. and Sanghavi, S. (2013) Low-Rank Matrix Completion Using Alternating Minimization. In: Proceedings of the Forty-Fifth Annual ACM Symposium on Theory of Computing, ACM, New York, 665-675. https://doi.org/10.1145/2488608.2488693
[25]	Jennings, A. (1967) A Direct Iteration Method for Obtaining Latent Roots and Vectors of a Symmetric Matrix. Proceedings of the Cambridge Philosophical Society, 63, 755-765. https://doi.org/10.1017/S030500410004175X
[26]	Jennings, A. (1977) Matrix Computations for Engineers and Scientists. Wiley, London.
[27]	Kiers, H.A.L. (2002) Setting up Alternating Least Squares and Iterative Majorization Algorithm for Solving Various Matrix Optimization Problems. Computational Statistics and Data Analysis, 41, 157-170. https://doi.org/10.1016/S0167-9473(02)00142-1
[28]	Kim, H. and Park, H. (2006) Sparse Non-Negative Matrix Factorizations via Alternating Non-Negativity-Constrained Least Squares. In: Proceedings of the IASTED International Conference on Computational and Systems Biology (CASB2006), ACM, New York, 95-100.
[29]	Kolda, T.G. and Bader, B.W. (2009) Tensor Decompositions and Applications. SIAM Review, 51, 455-500. https://doi.org/10.1137/07070111X
[30]	Koren, Y., Bell, R. and Volinsky, C. (2009) Matrix Factorization Techniques for Recommender Systems. Computer, 42, 30-37. https://doi.org/10.1109/MC.2009.263
[31]	Krijnen, W.P. (2006) Convergence of the Sequences of Parameters Generated by Alternating Least Squares Algorithms. Computational Statistics and Data Analysis, 5, 481-489. https://doi.org/10.1016/j.csda.2005.09.003
[32]	Kuroda, M., Mori, Y., Lizuka, M. and Sakakihara, M. (2011) Acceleration of the Alternative Least Squares Algorithm. Computational Statistics and Data Analysis, 55, 143-153. https://doi.org/10.1016/j.csda.2010.06.001
[33]	Larsen, R.M. (1998) Lanczos Bidiagonalization with Partial Reorthogonalization. Ph.D. Thesis, University of Aarhus, Aarhus, Denmark. https://doi.org/10.7146/dpb.v27i537.7070
[34]	Larsen, R.M. Combining Implicit Restarts and Partial Reorthogonalization in Lanczos Bidiagonalization. http://soi.stanford.edu/rmunk/PROPACK/
[35]	Lee, D.D. and Seung, H.S. (1999) Learning the Parts of Objects by Nonnegative Matrix Factorization. Nature, 401, 788-791. https://doi.org/10.1038/44565
[36]	Lee, D.D. and Seung, H.S. (2001) Algorithms for Nonnegative Matrix Factorization. Advances in Neural Information Processing, 13, 556-562.
[37]	de Leeuw, J., Young, F.W. and Takane, Y. (1976) Additive Structure in Qualitative Data: An Alternating Least Squares Method with Optimal Scaling Features. Psychometrika, 4, 471-503. https://doi.org/10.1007/BF02296971
[38]	Oseledets, I.V., Rakhuba, M. and Uschmajew, A. (2018) Alternating Least Squares as Moving Subspace Correction. SIAM Journal on Numerical Analysis, 56, 3459-3479. https://doi.org/10.1137/17M1148712
[39]	Parlett, B.N. (1980) The Symmetric Eigenvalue Problem. Prentice-Hall, Englewood Cliffs, NJ.
[40]	Rutishauser, H. (1969) Computational Aspects of F.L. Bauer’s Simultaneous Iteration Method. Numerische Mathematik, 13, 4-13. https://doi.org/10.1007/BF02165269
[41]	Rutishauser, H. (1970) Simultaneous Iteration Method for Symmetric Matrices. Numerische Mathematik, 16, 205-223. https://doi.org/10.1007/BF02219773
[42]	Saad, Y. (2011) Numerical Methods for Large Eigenvalue Problems. Revised Edition, SIAM, Philadelphia, PA. https://doi.org/10.1137/1.9781611970739
[43]	Sorensen, D.C. (1992) Implicit Application of Polynomial Filters in a k-Step Arnoldi Method. SIAM Journal on Matrix Analysis and Applications, 13, 357-385. https://doi.org/10.1137/0613025
[44]	Stewart, G.W. (1969) Accelerating the Orthogonal Iteration for the Eigenvectors of a Hermitian Matrix. Numerische Mathematik, 13, 362-376. https://doi.org/10.1007/BF02165413
[45]	Stewart, G.W. (1998) Matrix Algorithms, Vol. I: Basic Decompositions. SIAM, Philadelphia. https://doi.org/10.1137/1.9781611971408
[46]	Stewart, G.W. (2001) Matrix Algorithms, Vol. II: Eigensystems. SIAM, Philadelphia. https://doi.org/10.1137/1.9780898718058
[47]	Takane, Y., Young, F.W. and de Leeuw, J. (1977) Nonmetric Individual Differences Multidimensional Scaling: An Alternating Least Squares Method with Optimal Scaling Features. Psychometrika, 42, 7-67. https://doi.org/10.1007/BF02293745
[48]	Uschmajew, A. (2012) Local Convergence of the Alternating Least Squares Algorithm for Canonical Tensor Approximation. SIAM Journal on Matrix Analysis and Applications, 33, 639-652. https://doi.org/10.1137/110843587
[49]	Wang, L. and Chu, M.T. (2014) On the Global Convergence of the Alternating Least Squares Method for Rank-One Approximation to Generic Tensors. SIAM Journal on Matrix Analysis and Applications, 35, 1058-1072. https://doi.org/10.1137/130938207
[50]	Wang, L., Chu, M.T. and Yu, B. (2015) Orthogonal Low Rank Tensor Approximation: Alternating Least Squares Method and Its Global Convergence. SIAM Journal on Matrix Analysis and Applications, 36, 1-19. https://doi.org/10.1137/130943133
[51]	Wu, K. and Simon, H. (2000) Thick-Restarted Lanczos Method for Large Symmetric Eigenvalue Problems. SIAM Journal on Matrix Analysis and Applications, 22, 602-616. https://doi.org/10.1137/S0895479898334605
[52]	Young, F.W., de Leeuw, J. and Takane, Y. (1976) Regression with Qualitative and Quantitative Variables: An Alternating Least Squares Method with Optimal Scaling Features. Psychometrika, 41, 505-529. https://doi.org/10.1007/BF02296972
[53]	Young, F.W., Takane, Y. and de Leeuw, J. (1978) Principal Components of Mixed Measurement Level Multivariate Data: An Alternating Least Squares Method with Optimal Scaling Features. Psychometrika, 43, 279-281. https://doi.org/10.1007/BF02293871
[54]	Zacharih, D., Sundin, M., Jansson, M. and Chatterjee, S. (2012) Alternating Least-Squares for Low-Rank Matrix Reconstruction. Signal Processing Letters, 19, 231-234. https://doi.org/10.1109/LSP.2012.2188026