Approximate Reformulation a Recent Non-Renormalizable QFT’s Methodology and Einstein’s Gravity

A. Plastino^1,2,3, M. C. Rocca^1,2,4

¹Departamento de Fisica, Universidad Nacional de La Plata, Argentina.
²Consejo Nacional de Investigaciones Científicas y Tecnológicas (IFLP-CCT-CONICET)-C. C. 727, La Plata, Argentina.
³SThAR-EPFL, Lausanne, Switzerland.
⁴Departamento de Matemática, Universidad Nacional de La Plata, Argentina.

DOI: 10.4236/jhepgc.2020.62023                

Abstract

We revisit, advancing a useful approximation, a recently formulated QFT treatment that successfully overcomes any troubles with infinities for non-renormalizable QFTs [J. Phys. Comm. 2 115029 (2018)]. Such methodology was able to successfully deal, in non-relativistic fashion, with Newton’s gravitation potential [Annals of Physics 412, 168013 (2020)]. Our present approximation to the QFT method of [J. Phys. Comm. 2 115029 (2018)] is based on the Einstein’s Lagrangian (EG) elaborated by Gupta [1], save for a different constraint’s selection. This choice allows one to avoid the lack of unitarity for the S matrix that impaired the proceedings of Gupta and Feynman. Moreover, we are able to simplify the handling of such constraint by eliminating the need to involve ghosts for guarantying unitarity. Our approximation consists in setting the graviton field ∅^μν=γ^μν∅, where γ^μν is a constant tensor and ∅ a scalar (graviton) field. The ensuing approximate approach is non-renormalizable, an inconvenience that we are able to overcome in [J. Phys. Comm. 2 115029 (2018)].

Keywords

Quantum Field Theory, Einstein Gravity, Non-Renormalizable Theories, Unitarity

1. Introduction

Quantifying Einstein gravity (EG) remains an open problem. We can speak of the Holy Grail for quantum field theory (QFT). Many preceding attempts in this vein failed because 1) they use Rigged Hilber Space (RHS) with undefined metric, 2) non-unitarity troubles, and iii) non-renormalizablity problems.

We will construct here a unitary EG’s QFT based on efforts by Gupta [1], but deviate from his path by appealing to a distinct EG-constraint. This technical detail poses a problem analogous to that of Quantum Electrodynamics (QED). To quantize the associated non-renormalizable variational problem, we employ mathematical tools developed by Bollini et al. [2] [3] [4] [5] [6] in the wake of Ultra distributions introduced by J. S. Silva (JSS) [7], also called Ultrahyperfunctions. The above cited mathematical apparatus was specifically devised so as to quantify non-renormalizable field theories, for a detailed discussion see [2] [3] [4] [5] [6]. One ends up facing a theory similar to QED, endowed with unitarity at all finite orders in power expansions in the gravitation constant G of the EG Lagrangian. This was previously attempted, but without success, by Gupta and by Feynman (in his celebrated Acta Physica Polonica paper [8]).

Rather surprisingly for some contemporary physicists, for a mathematician, quantifying a non-renormalizable field theory is equivalent to properly defining a product of two distributions (a product in a ring with zero-divisors in configuration space). This is an old problem in functional theory, successfully tackled in [2] [3] [4] [5] [6].

Remember that, in QFT, evaluating products of distributions with coincident point singularities is connected to the asymptotic behavior of loop integrals of propagators.

In [2] [3] [4] [5] the authors showed the feasibility of defining a general convolution between the ultrahyperfunctions of JSS [7]. This convolution produces another ultrahyperfunction. Thus, one has a product in a ring with zero divisors, a ring that is the space of distributions of exponential type, or ultradistributions of exponential type. We get them applying the anti-Fourier transform to the space of tempered ultra distributions or ultra distributions of exponential type.

The ultrahyperfunctions are just the generalization and extension to the complex plane of the Schwartz tempered distributions and the distributions of exponential type. Thus, the tempered distributions and those of exponential type are a subset of the ultrahyprefunctions.

The present work we do not employ counter-terms to eliminate infinities, since our convolutions remain always finite. One should not wish for counter-terms, since a non-renormalizable theory involves an infinite number of them.

Simultaneously, we keep all extant solutions to the problem of running coupling constants and the renormalization group. Our convolution, once available, transforms configuration space into a ring with zero-divisors. In such ring, we have defined now a product between the ring-elements. Accordingly, any unitary-causal-Lorentz invariant theory quantified in such way becomes predictive. One does no need now to distinguish between renormalizable on non-renormalizable QFT’s.

Our convolution uses Laurent’s expansions in the parameter employed to define it. All finite constants of the convolutions become determined, eliminating arbitrary selections of finite constants. This is equivalent to deleting all finite renormalizations of the theory. The independent term in the Laurent expansion yields the convolution value, which translates to configuration space the product-operation in a ring with divisors of zero.

Our paper is structured as indicated belows:

1) Section 2 deals with preliminary materials.

2) Section 3 treats the QFT Lagrangian for EG and introduces a new approximation that consists in setting the graviton field ${\varphi }^{\mu \nu }={\gamma }^{\mu \nu }\varphi$ , where ${\gamma }^{\mu \nu }$ is a constant tensor and $\varphi$ a scalar (graviton) field.

3) Section 4 quantizes the ensuing theory.

4) Section 5 evaluates the graviton’s self-energy up to second order.

5) Section 6 introduces axions into our scenario and considers the axions gravitons interaction.

6) Section 7 calculates the graviton’s self-energy in the presence of axions.

7) Section 8 evaluates the axion’s self-energy, up to second order.

8) Finally, some conclusions are drawn in Section 9.

2. Preliminary Materials

The most general quantification approach is Schwinger-Feynman’s variational principle [9]. It is able to deal even with high order supersymmetric theories, as done by [10] [11]. These theories cannot be quantized by appeal to the customary Dirac-brackets approach.

Consider now the action for a set of fields written in the fashion

$\mathcal{S}\left[\sigma \left(x\right)\mathrm{,}{\sigma }_0\mathrm{,}{\varphi }_A\left(x\right)\right]={\displaystyle \underset{{\sigma }_0}{\overset{\sigma \left(x\right)}{\int }}}\mathcal{L}\left[{\varphi }_A\left(\xi \right)\mathrm{,}{\partial }_{\mu }{\varphi }_A\left(\xi \right)\mathrm{,}\xi \right]\text{d}\xi \mathrm{,}$ (2.1)

where $\sigma \left(x\right)$ if a space-like surface passing through the point x. ${\sigma }_0$ is that surface (at the remote past), for which all field variations vanish. The Schwinger-Feynman variational principle asserts that

“Any Hermitian infinitesimal variation $\delta \mathcal{S}$ of the action induces a canonical transformation of the vector space in which the quantum system is defined, and the generator of this transformation is this same operator $\delta \mathcal{S}$ ”.

Thus, this equality holds:

$\delta {\varphi }_A=i\left[\delta \mathcal{S}\mathrm{,}{\varphi }_A\right]\mathrm{.}$ (2.2)

Accordingly, for a Poincare transformation one has

$\delta \mathcal{S}=a^{\mu }{\mathcal{P}}_{\mu }+\frac{1}{2}{a}^{\mu v}{\mathcal{M}}_{\mu v}\mathrm{,}$ (2.3)

where the field variation is

$\delta {\varphi }_a=a^{\mu }{\hat{P}}_{\mu }{\varphi }_A+\frac{1}{2}{a}^{\mu v}{\hat{M}}_{\mu v}{\varphi }_A\mathrm{.}$ (2.4)

From (2) one ascertains that

${\partial }_{\mu }{\varphi }_A=i\left[{\mathcal{P}}_{\mu }\mathrm{,}{\varphi }_A\right]\mathrm{.}$ (2.5)

More to the point,

${\partial }_0{\varphi }_A=i\left[{\mathcal{P}}_0\mathrm{,}{\varphi }_A\right]\mathrm{.}$ (2.6)

Eq. (ep2.6) will be used below for quantizing EG.

3. The Lagrangian of Einstein’s QFT

The EG Lagrangian is [1]

${\mathcal{L}}_G=\frac{1}{{\kappa }^2}R\sqrt{\left|g\right|}-\frac{1}{2}{\eta }_{\mu v}{\partial }_{\alpha }{h}^{\mu \alpha }{\partial }_{\beta }{h}^{v\beta }\mathrm{,}$ (3.1)

where Minkowski’s ${\eta }^{\mu \nu }=diag\left(\mathrm{1,1,1,}-1\right)$ while $h^{\mu \nu }=\sqrt{\left|g\right|}{g}^{\mu \nu }$ The second term in (3.1) establishes the gauge fixing. We reach here a critical stage by proceeding to perform a crucial linear approximation. This will be immediately seen to be an approximation to the graviton field. We write:

$h^{\mu v}={\eta }^{\mu v}+\kappa {\varphi }^{\mu v}\mathrm{,}$ (3.2)

where ${\kappa }^2$ is the gravitation’s constant and ${\varphi }^{\mu v}$ the graviton field. Our approximation based in [12] reads

${\varphi }^{\mu v}={\gamma }^{\mu v}\varphi \mathrm{,}$ (3.3)

with $\varphi$ a scalar field and where ${\gamma }^{\mu v}$ is a constant tensor which satisfies

${\gamma }_{\mu }^{\mu }=0$ (3.4)

This approximate casting of ${\varphi }^{\mu v}$ considerably simplifies the handling of matters without sacrifice of rigor. We write now the Lagrangian as a sum of a non-perturbative component plus an interactions one, i.e.,

${\mathcal{L}}_G={\mathcal{L}}_L+{\mathcal{L}}_I\mathrm{,}$ (3.5)

where

${\mathcal{L}}_L=-\frac{1}{4}{\gamma }_{\mu v}{\gamma }^{\mu v}{\partial }_{\lambda }\varphi {\partial }^{\lambda }\varphi \mathrm{,}$ (3.6)

and, up to 2nd order, one has [1]

${\mathcal{L}}_I=-\frac{1}{2}\kappa {\gamma }^{\mu v}\varphi \left[\frac{1}{2}{\gamma }_{\rho \lambda }{\gamma }^{\rho \lambda }{\partial }_{\mu }\varphi {\partial }_v\varphi +{\gamma }_{\mu \beta }{\gamma }_{\lambda v}{\partial }^{\lambda }\varphi {\partial }^{\beta }\varphi -{\gamma }_{\mu \rho }{\gamma }_v^{\rho }{\partial }_{\lambda }\varphi {\partial }^{\lambda }\varphi \right]\mathrm{,}$ (3.7)

having made use of the constraint (3.4) This constraint is required in order to satisfy gauge invariance [13] For the field $\varphi$ we have then, as can also be seen to happen in [6],

$\square \varphi =\mathrm{0,}$ (3.8)

whose solution is

$\varphi \left(x\right)=\frac{1}{{\left(2\pi \right)}^{\frac{3}{2}}}{\displaystyle \int }\left[\frac{a\left(k\right)}{\sqrt{2k_0}}{\text{e}}^{i{k}_{\mu }{x}^{\mu }}+\frac{a^{+}\left(k\right)}{\sqrt{2k_0}}{\text{e}}^{-i{k}_{\mu }{x}^{\mu }}\right]{\text{d}}^{3}k\mathrm{,}$ (3.9)

with $k_0=\left|k\right|$ . Above, $a\left(k\right)$ and $a^{+}\left(k\right)$ stand for Fourier coefficients. Up to this point we were using Einstein’s Lagrangian. Its quantization begins next.

4. The Quantization of the Theory

As usual in QFT, see for instance Visconti’ celebrated book [9], the quantum energy-momentum tensor $T_{\rho }^{\lambda }$ is cast as

$T_{\rho }^{\lambda }=\frac{\partial \mathcal{L}}{\partial {\partial }^{\rho }{\varphi }^{\mu v}}{\partial }^{\lambda }{\varphi }^{\mu v}-{\delta }_{\rho }^{\lambda }\mathcal{L}\mathrm{,}$ (4.1)

and the time-component of the four-momentum is now the quantum operator

${\mathcal{P}}_0={\displaystyle \int }{T}_0^0{\text{d}}^{3}x\mathrm{.}$ (4.2)

Using (3.4) we have

$T_0^0=-\frac{1}{4}{\gamma }_{\mu v}{\gamma }^{\mu v}\left[{\partial }_0\varphi {\partial }^0\varphi -{\partial }_j\varphi {\partial }^j\varphi \right]\mathrm{.}$ (4.3)

Consequently,

${\mathcal{P}}_0=\frac{1}{4}{\gamma }_{\mu v}{\gamma }^{\mu v}{\displaystyle \int }\left|k\right|\left[a\left(k\right)a^{+}\left(k\right)+a^{+}\left(k\right)a\left(k\right)\right]{\text{d}}^{3}k\mathrm{.}$ (4.4)

Appeal to (2.6) leads now to

$\left[{\mathcal{P}}_0\mathrm{,}{a}^{+}\left(k\right)\right]=k_0{a}^{+}\left(k\right)\mathrm{.}$ (4.5)

From the last relation in (4.5) one gathers that

$\left|k\right|a^{+}\left(k^{\prime }\right)=\frac{{\gamma }_{\mu v}{\gamma }^{\mu v}}{2}{\displaystyle \int }\left|k\right|\left[a\left(k\right)\mathrm{,}{a}^{+}\left(k^{\prime }\right)\right]a^{+}\left(k\right){\text{d}}^{3}k\mathrm{.}$ (4.6)

The solution of this integral equation is

$\left[a\left(k\right)\mathrm{,}{a}^{+}\left(k^{\prime }\right)\right]=\frac{2}{{\gamma }_{\mu v}{\gamma }^{\mu v}}\delta \left(k-k^{\prime }\right)\mathrm{.}$ (4.7)

We use now the the usual definition

$\Delta \left(x-y\right)=\langle 0|T\left[\varphi \left(x\right)\varphi \left(y\right)\right]|0\rangle \mathrm{.}$ (4.8)

The graviton’s propagator then turns out to be

$\Delta \left(x-y\right)=\frac{i}{{\left(2\pi \right)}^4}\frac{2}{{\gamma }_{\mu v}{\gamma }^{\mu v}}{\displaystyle \int }\frac{{\text{e}}^{i{k}_{\mu }\left(x^{\mu }-y^{\mu }\right)}}{k^2-i0}{\text{d}}^{4}k\mathrm{.}$ (4.9)

As a consequence, we can write

${\mathcal{P}}_0=\frac{{\gamma }_{\mu v}{\gamma }^{\mu v}}{4}{\displaystyle \int }\left|k\right|\left[a\left(k\right)a^{+}\left(k^{\prime }\right)+a^{+}\left(k^{\prime }\right)a\left(k\right)\right]\delta \left(k-k^{\prime }\right){\text{d}}^{3}k{\text{d}}^3{k}^{\prime }\mathrm{,}$ (4.10)

or

${\mathcal{P}}_0=\frac{{\gamma }_{\mu v}{\gamma }^{\mu v}}{4}{\displaystyle \int }\left|k\right|\left[2a^{+}\left(k^{\prime }\right)a\left(k\right)+\frac{2}{{\gamma }_{\rho \lambda }{\gamma }^{\rho \lambda }}\delta \left(k-k^{\prime }\right)\right]\delta \left(k-k^{\prime }\right){\text{d}}^{3}k{\text{d}}^3{k}^{\prime }\mathrm{.}$ (4.11)

Thus, we obtain

${\mathcal{P}}_0=\frac{{\gamma }_{\mu v}{\gamma }^{\mu v}}{2}{\displaystyle \int }\left|k\right|a^{+}\left(k\right)a\left(k\right){\text{d}}^{3}k\mathrm{,}$ (4.12)

where we have used the fact that the product of two deltas with the same argument vanishes [2], i.e.,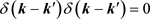. This illustrates the fact that using Ultrahyperfunctions is here equivalent to adopting the normal order in the definition of the time-component of the four-momentum

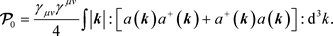(4.13)

Now, we must insist on the fact that the physical state should satisfy the relation (see [1])

(4.14)

The ensuing theory is similar to the QED-one obtained via the quantization approach of Gupta-Bleuler. This implies that the theory is unitary for any finite perturbative order. In this theory just one type of graviton arises, , while in Gupta’s treatment two sorts of graviton emerge. Of course, this happens for a non-interacting theory, as pointed out by Gupta.

5. Graviton’s Self Energy

So as to compute the graviton’s self-energy (SF)c we begin with the interaction Hamiltonian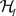. Remark that the Lagrangian has derivative interaction terms.

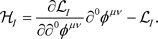(5.1)

A typical term reads

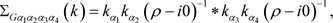(5.2)

where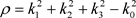

In dimensions, the Fourier transform of (2) becomes

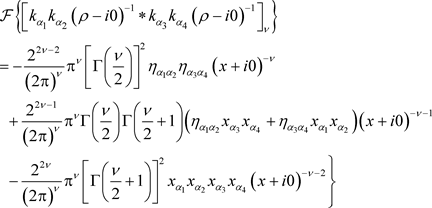(5.3)

where.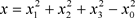

Anti-transforming the above equation one has

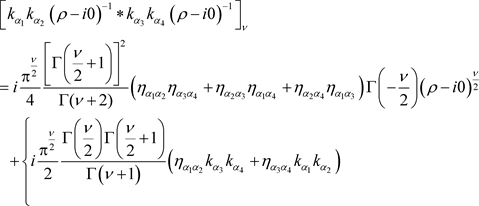
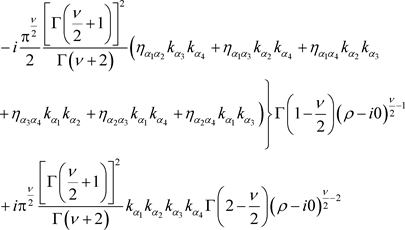(5.4)

Computing the Self-Energy in Dimensions

We proceed here to perform a -Laurent expansion, keeping from it the independent term [6]. We Laurent-expand (5.4) around and encounter

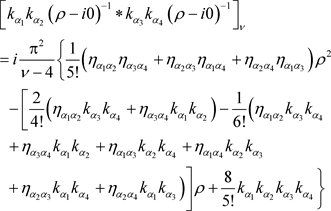
(5.5)

The exact value of the convolution we are interested in, i.e., the left hand side of (5.5), is given by the independent term above, as everyone knows. Should the reader be unfamiliar with this scenario, we direct him/her to [6]. We now get

(5.6)

We face here 1296 diagrams of this type.

6. Axions Enter the Picture

Axions are hypothetical elementary particles conjectured by the 1977 Peccei-Quinn theory so as to tackle the strong CP problem in quantum chromodynamics. Should they exist and have low enough mass (within a certain range), they may be of some interest as putative components of cold dark matter [14]. We thus consider now a massive scalar field (axions) interacting with the graviton and the pertinent Lagrangian becomes

(6.1)

It is possible to recast the Lagrangian now as

(6.2)

where

(6.3)

so that is the Lagrangian for the axion-graviton action

(6.4)

A new term in the interaction Hamiltonian appears

(6.5)

7. Graviton’s Complete Self Energy

Axions necessarily generate a new contribution to a graviton’s self energy

(7.1)

To evaluate it face the customary dimensional integral together with the Feynman-parameters denoted by the letter x. After a Wick rotation we find

(7.2)

where

(7.3)

Effecting a variables-change we encounter

(7.4)

where

(7.5)

After computing the associated integrals we find

(7.6)

Computing the Self-Energy ()

We appeal once again to a Laurent’s expansion and have

(7.7)

Once again, the exact result for our four-dimensional convolution is

(7.8)

Accordingly, our desired self-energy total is a combination of and.

8. Axion’s Self Energy

The self-energy reads

(8.1)

In dimensions we have

(8.2)

Using the same Feynman parameters as above we have

(8.3)

where

(8.4)

We compute the integral (8.3) and encounter

(8.5)

Self-Energy Computation ()

We Laurent-expand again, this time (8.5) around.

(8.6)

The -independent term yields the exact convolution result we need

(8.7)

9. Conclusions

We have developed above an approximate quantum field theory (QFT) of Eintein’s gravity (EG) that is both unitary and finite. It critically necessitates of a new constraint-introduction in the EG-Lagrangian. Laurent expansions were a main tool for our endeavors. Our approximation consists in defining the graviton field as with a constant tensor and a scalar field. Our mathematical apparatus has been developed by Bollini et al. [2] [3] [4] [5] [6] and is powerful enough so as to be able to quantize non-renormalizable field theories [2] [3] [4] [5] [6]. We have evaluated in finite fashion

• a graviton’s self-energy in the EG-field,

• the self-energy in the presence of a massive scalar field (axions, for example). Two sorts of diagram emerge: the original ones of the pure EG field plus the ones generated by the addition of a scalar field.

• An axion’s self-energy.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Gupta, S.N. (1952) Quantization of Einstein's Gravitational Field: General Treatment. Proceedings of the Physical Society. Section A, 65, 161. https://doi.org/10.1088/0370-1298/65/8/304
[2]	Bollini, C.G., Escobar, T. and Rocca, M.C. (1999) Convolution of Ultradistributions and Field Theory. International Journal of Theoretical Physics, 38, 2315-2332. https://doi.org/10.1023/A:1026623718239
[3]	Bollini, C.G. and Rocca, M.C. (2004) Convolution of Lorentz Invariant Ultradistributions and Field Theory. International Journal of Theoretical Physics, 43, 1019-1051. https://doi.org/10.1023/B:IJTP.0000048599.21501.93
[4]	Bollini, C.G. and Rocca, M.C. (2004) Convolution of n-Dimensional Tempered Ultradistributions and Field Theory. International Journal of Theoretical Physics, 43, 59-76. https://doi.org/10.1023/B:IJTP.0000028850.35090.24
[5]	Bollini, C.G., Marchiano, P. and Rocca, M.C. (2007) Convolution of Ultradistributions, Field Theory, Lorentz Invariance and Resonances. International Journal of Theoretical Physics, 46, 3030-3059. https://doi.org/10.1007/s10773-007-9418-y
[6]	Plastino, A. and Rocca, M.C. (2018) Quantum Field Theory, Feynman-, Wheeler Propagators, Dimensional Regularization in Configuration Space and Convolution of Lorentz Invariant Tempered Distributions. Journal of Physics Communications, 2, Article ID: 115029. https://doi.org/10.1088/2399-6528/aaf186
[7]	Sebastiao e Silva, J. (1958) Les fonctions analytiques comme ultra-distributions dans le calcul opérationnel. Mathematische Annalen, 136, 38. https://doi.org/10.1007/BF01350287
[8]	Feynman, R.P. (1963) Quantum Theory of Gravitation. Acta Physica Polonica, 24, 697.
[9]	Visconti, A. (1969) Quantum Field Theory. Pergamon Press, London.
[10]	Delbourgo, R. and Prasad, V.B. (1975) Supersymmetry in the Four-Dimensional Limit. Journal of Physics G: Nuclear Physics, 1, 377. https://doi.org/10.1088/0305-4616/1/4/001
[11]	Barci, D.G., Bollini, C.G. and Rocca, M.C. (1995) Quantization of a Six-Dimensional Wess-Zumino Model. Il Nuovo Cimento, 108, 797-808. https://doi.org/10.1007/BF02731021
[12]	Plastino, A. and Rocca, M.C. Gupta-Feynman Based Quantum Field Theory of Einstein’s Gravity. https://www.researchgate.net/publication/336406184_Gupta-Feynman_based_Quantum_Field_ Theory_of_Einstein's_Gravity
[13]	Kleinert, H. (2016) Particles and Quantum Fields Free Web Version. https://doi.org/10.1142/9915
[14]	Peccei, R.D. (2008) The Strong CP Problem and Axions. In: Kuster, M., Raffelt, G. and Beltrán, B., Eds., Axions: Theory, Cosmology, and Experimental Searches, Lecture Notes in Physics, Springer, Berlin, 3-17. https://doi.org/10.1007/978-3-540-73518-2_1