Autoregressive Fractionally Integrated Moving Average-Generalized Autoregressive Conditional Heteroskedasticity Model with Level Shift Intervention

Lawrence Dhliwayo¹, Florance Matarise¹, Charles Chimedza²

¹Department of Statistics, University of Zimbabwe, Harare, Zimbabwe.
²School of Statistics and Actuarial Science, University of Witwatersrand, Johannesburg, South Africa.

DOI: 10.4236/ojs.2020.102023                

Abstract

In this paper, we introduce the class of autoregressive fractionally integrated moving average-generalized autoregressive conditional heteroskedasticity (ARFIMA-GARCH) models with level shift type intervention that are capable of capturing three key features of time series: long range dependence, volatility and level shift. The main concern is on detection of mean and volatility level shift in a fractionally integrated time series with volatility. We will denote such a time series as level shift autoregressive fractionally integrated moving average (LS-ARFIMA) and level shift generalized autoregressive conditional heteroskedasticity (LS-GARCH). Test statistics that are useful to examine if mean and volatility level shifts are present in an autoregressive fractionally integrated moving average-generalized autoregressive conditional heteroskedasticity (ARFIMA-GARCH) model are derived. Quasi maximum likelihood estimation of the model is also considered.

Keywords

Fractional Differencing, Long-Memory, Heteroscedasticity, Volatility, Level Shift

1. Introduction

When dealing with empirical time series from diverse fields of application, we are confronted with the phenomenon of long memory or long range dependence. A popular way to analyze a long memory time series is to use autoregressive fractionally integrated moving average (ARFIMA) processes introduced by [1] and [2]. The works of [1] and [2] assume that the conditional variance of the time series is constant over time. However, non constant variance in non-linear time series is a challenging modelling exercise, considered among other things by [3]. In particular, the stylized fact that the volatility of financial time series is non constant has been long recognized in literature, see for example [4] [5] and [6].

Thus, the methodology for modelling time series with long memory behavior has been extended to long memory time series with time varying conditional variance. See for instance, [7] who developed the ARFIMA model with generalized autoregressive conditional heteroskedasticity (GARCH) type innovations, and [8] examine the daily average PM₁₀ concentration using a seasonal ARFIMA model with GARCH errors. Tong [9] analyse the nonlinear time series using GARCH models and [10] used GARCH models for testing market efficiency. These models do not capture level shifts both in mean and variance; in this paper we introduce a new class of ARFIMA-GARCH models with mean and volatility level shift intervention. This approach allows us to model mean and volatility level shifts in an ARFIMA-GARCH model, which are often observed in financial or economics time series.

The model to be developed combines ideas from different strands of the statistical, financial and econometric literature. Autoregressive Moving Average (ARMA) models are extensively discussed in [11]. The fractional differencing model introduced by [12] has become a standard model for long-memory behaviour. The generalization towards the ARFIMA model with no periodic coefficients was introduced by [1] and [2]. Statistical properties and inferences for ARFIMA and other long-memory processes were discussed extensively by [13], [14] and [15]. On the other hand, the GARCH model was developed by [16] and [4]. The statistical properties of GARCH processes are well established, see for example [17].

This article introduces detection of a mean and volatility level shifts innovation in an ARFIMA-GARCH model. The works of [18] first applied ARFIMA-GARCH models to price indices then [7] derived conditions for asymptotic normality of the approximate (Gaussian) maximum likelihood (ML) estimator in the ARFIMA-GARCH model. This paper also extends parameter estimation for an ARFIMA-GARCH model to case with level shift which we will denote Level Shift ARFIMA (LS-ARFIMA) and Level Shift GARCH (LS-GARCH) using quasi-maximum likelihood estimation.

The first concern of this paper is how one would formally address modeling mean and volatility level shifts in an ARFIMA-GARCH. The second concern is derivation of test statistics that are useful to examine presence of level shifts in mean and volatility for an ARFIMA-GARCH model. The layout of the paper is organised as follows. Section 2 reviews some theoretical results of ARFIMA and GARCH. In Section 3, we introduce the class of LS-ARFIMA-LS-GARCH models. Section 4 deals with parameter estimation in LS-ARFIMA and LS-GARCH models. Section 5 is dedicated to the proposed procedure of level shift detection in ARFIMA-GARCH models. In Section 6, we perform some simulation study of the mean and volatility level shift detection procedure. The last section concludes with the main findings and limitations. Common acronyms used in this paper are given in Table 1.

Table 1. Common acronyms used in this paper.

2. Some Theoretical Results

This section presents some theoretical literature on ARFIMA models and GARCH models. An overview of ARFIMA-GARCH models is also presented.

2.1. The ARFIMA Model

The study of time series turned attention to incorporate long memory or long-range dependence characteristics. The ARFIMA(p, d, q) process, first introduced by [1] and [2], present this property when the differencing parameter d is in the interval (0, 0.5). This feature is reflected by the hyperbolic decay of its autocorrelation function or by the unboundedness of its spectral density function, while in the ARMA model, dependency between observations decays at a geometric rate.

Montanari et al. [19] introduced a special form of the generalized ARFIMA model and also considered by [20]. This formulation is able to reproduce short- and long-memory periodicity in the autocorrelation function of the process. Using the [11] notation, let ${\left\{y_t\right\}}_{t\in \mathbb{Z}}$ be a stochastic process, then ${\left\{y_t\right\}}_{t\in \mathbb{Z}}$ is an ARFIMA process given by the expression

$\varphi \left(B\right){\left(1-B\right)}^d\left(y_t-{\mu }_0\right)=\theta \left(B\right){\epsilon }_t\mathrm{,\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\text{for}t\in \mathbb{Z}\mathrm{,}$ (1)

where ${\mu }_0$ is the mean of the process, ${\left\{{\epsilon }_t\right\}}_{t\in \mathbb{Z}}$ is a white noise process with zero mean and variance ${\sigma }_{\epsilon }^2=\mathbb{E}\left({\epsilon }_t^2\right)$ , B is the backward-shift operator, that is, $B^k{X}_t=X_{t-k}$ , $\varphi (\cdot )$ and $\theta (\cdot )$ are the polynomials of degrees p and q, respectively, defined by

$\varphi \left(B\right)=1+{\displaystyle \underset{i=1}{\overset{p}{\sum }}}\left(-{\varphi }_i\right)B^i\mathrm{<mi>\; </mi>\; <mi>\; </mi>}\text{and}\mathrm{<mi>\; </mi>\; <mi>\; </mi>}\theta \left(B\right)=1+{\displaystyle \underset{j=1}{\overset{q}{\sum }}}\left({\theta }_j\right)B^j$ (2)

where, ${\varphi }_i\mathrm{,\; <mi>\; </mi>\; 1}\le i\le p$ , and ${\theta }_j\mathrm{,\; <mi>\; </mi>\; 1}\le j\le q$ are constants.

The difference operator ${\left(1-B\right)}^d$ is defined by means of the binomial expansion ${\left(1-B\right)}^d$ and can be expressed as:

${\left(1-B\right)}^d={\displaystyle \underset{i=0}{\overset{\infty }{\sum }}}\left(\begin{array}{c}d\\ i\end{array}\right){\left(-B\right)}^i={\displaystyle \underset{i=0}{\overset{\infty }{\sum }}}\frac{\left(i+d-1\right)!}{i!\left(d-1\right)!}{B}^i.$ (3)

The ARFIMA model is said to be stationary when $-0.5<d<0.5$ , where the effect of shocks to ${\epsilon }_t$ decays at a gradual rate to zero. The model becomes nonstationary when $d\ge 0.5$ and stationary but non invertible when $d\le -0.5$ , which means the time series is impossible to model for any AR process. With regard to the modeling of data dependencies, the ARFIMA model represents a short memory if $d=0$ , where the effect of shocks decays geometrically; and a unit root process is shown when $d=1$ . Furthermore, the model has a positive dependence among distance observations or the so called long memory process if $0<d<0.5$ ; and it also has an anti-persistent property or has an intermediate memory if $-0.5<d<0$ .

2.2. The GARCH(r, s) Model

The GARCH(r, s) model can be obtained from Equation (1) by letting

$E\left[{\epsilon }_t\mathrm{<mo>\; |\; </mo>}{F}_{t-1}\right]=0$ and the conditional variance, $E\left[{\epsilon }_t^2\mathrm{<mo>\; |\; </mo>}{F}_{t-1}\right]=h_t$ where $F_{t-1}$ is the $\sigma$ field generated by the past information $\left\{{\epsilon }_{t-1}\mathrm{,}{\epsilon }_{t-2},\cdots \right\}$ . Let also ${\epsilon }_t\mathrm{<mo>\; |\; </mo>}{F}_{t-1}~N\left(\mathrm{0,}{h}_t\right)$ and

${\epsilon }_t=z_t\sqrt{h_t}$ (4)

where $z_t$ is normal distributed with mean 0 and variance 1. Bollerslev [4] introduced the GARCH(r, s) model which defines the conditional variance equation as follows:

$h_t={\omega }_0+{\displaystyle \underset{i=1}{\overset{r}{\sum }}}{\alpha }_i{\epsilon }_{t-i}^2+{\displaystyle \underset{i=1}{\overset{s}{\sum }}}{\beta }_i{h}_{t-i}$ (5)

where ${\omega }_0>0$ , ${\alpha }_1\mathrm{,}\cdots \mathrm{,}{\alpha }_r\mathrm{,}{\beta }_1\mathrm{,}\cdots \mathrm{,}{\beta }_s\ge 0$ , r and s are positive integer. Yang and Wang [21] applied the GARCH model based on ARIMA model in data analysis. Note that the GARCH model defined by (5) can be replaced by other conditional heteroscedastic models.

2.3. The General ARFIMA(p, d, q)-GARCH(r, s) Model

Let the ARFIMA(p, d, q)-GARCH(r, s) model be the discrete time series model of $\left\{y_t\right\}$ given by the following equation:

$\begin{array}{l}{y}_t={\mu }_0+{\varphi }^{-1}\left(B\right){\left(1-B\right)}^{-d}\theta \left(B\right){\epsilon }_t\\ {\epsilon }_t=z_t\sqrt{h_t},\mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}{\epsilon }_t|F_{t-1}~N\left(0,h_t\right)\\ h_t={\omega }_0+{\displaystyle \underset{i=1}{\overset{r}{\sum }}}{\alpha }_i{\epsilon }_{t-i}^2+{\displaystyle \underset{i=1}{\overset{s}{\sum }}}{\beta }_i{h}_{t-i}\end{array}$ (6)

The following theorem shows some properties of ARFIMA(p, d, q)-GARCH(r, s) models.

Let $\left\{y_t\right\}$ be generated by model (6). Suppose that all roots of $\varphi \left(B\right)$ and

$\theta \left(B\right)$ lie outside the unit circle and ${\displaystyle \underset{i=1}{\overset{r}{\sum }}}{\alpha }_i+{\displaystyle \underset{j=1}{\overset{s}{\sum }}}{\beta }_j<1$ .

1) If $d<\frac{1}{2}$ , then $\left\{y_t\right\}$ is second-order stationary and has the following representation:

$y_t={\mu }_0+{\varphi }^{-1}\left(B\right)\theta \left(B\right){\displaystyle \underset{i=0}{\overset{\infty }{\sum }}}\frac{\left(i+d-1\right)\mathrm{<mo>\; !\; </mo>}}{i\mathrm{<mo>\; !\; </mo>}\left(d-1\right)\mathrm{<mo>\; !\; </mo>}}{\epsilon }_{t-i}\mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}a\mathrm{.}s\mathrm{.}$ (7)

Hence $\left\{y_t\right\}$ is strictly stationary and ergodic.

2) If $d>-\frac{1}{2}$ , then $\left\{y_t\right\}$ is invertible, that is, ${\epsilon }_t$ can be written as

${\epsilon }_t=\varphi \left(B\right){\theta }^{-1}\left(B\right){\displaystyle \underset{i=0}{\overset{\infty }{\sum }}}\frac{\left(i-d-1\right)\mathrm{<mo>\; !\; </mo>}}{i\mathrm{<mo>\; !\; </mo>}\left(-d-1\right)\mathrm{<mo>\; !\; </mo>}}\left(y_{t-i}-{\mu }_0\right)\mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}a\mathrm{.}s\mathrm{.}$ (8)

For proof of Theorem (2.3) see [22].

2.4. Variance of Variance in the Standard GARCH(1, 1) Model

By rearranging the conditional variance Equation (5) for a GARCH(1, 1) we obtain:

$\begin{array}{c}{h}_t={\omega }_0+\left({\alpha }_1+{\beta }_1\right)h_{t-1}+{\alpha }_1\left({ϵ}_{t-1}^2-h_{t-1}\right)\\ ={\omega }_0+\gamma h_{t-1}+{\alpha }_1{h}_{t-1}{\eta }_{t-1}\end{array}$ (9)

where $\gamma ={\alpha }_1+{\beta }_1$ and ${\eta }_t=z_t^2-1$ . Ishida and Engle [23] have shown that the variance of variance is given by:

$Var\left(h_t\right)={\alpha }_1^2{h}_{t-1}E\left[{\eta }_{t-1}\right]=\left({\kappa }_z-1\right){\alpha }_1^2{h}_{t-1}^2$ (10)

where ${\kappa }_z$ denotes the conditional kurtosis of $z_t$ , which we assume to be finite constant. If the distribution of $z_t$ is standard normal, then ${\kappa }_z-1=2$ .

Ishida and Engle [23] further rearranged the terms in Equation (9), the conditional variance equation becomes:

$\begin{array}{c}{h}_t-h_{t-1}=\phi \left(\tau -h_{t-1}\right)+{\alpha }_1\sqrt{h_{t-1}}{\eta }_{t-1}\\ ={\omega }_0+\gamma h_{t-1}+{\alpha }_1\sqrt{h_{t-1}}{\eta }_{t-1}\end{array}$ (11)

where $\phi =1-\gamma$ determines the speed at which the conditional variance reverts to its long run mean $\tau =E\left(\tau \right)={\omega }_0{\left(1-\gamma \right)}^{-1}$ and its corresponding variance becomes:

$Var\left(h_t-h_{t-1}\right)=\left({\kappa }_z-1\right){\alpha }_1^2{h}_{t-1}$ (12)

Belkhouja and Mootamri [24] performed a long memory and structural change in the G7 inflation dynamics. The following section presents a natural extension of ARFIMA-GARCH models to the case with level shift.

3. ARFIMA-GARCH Models with Level Shift

This section presents a natural extension of the ARFIMA-GARCH models to a case with level shift. We start with a shift in the mean, then a shift in volatility and finally shift in both mean and volatility.

3.1. The ARFIMA(p, d, q) Model with Level Shift

The ARFIMA(p, d, q) model is written as

$\varphi \left(B\right){\left(1-B\right)}^d\left(y_t-{\mu }_0\right)=\theta \left(B\right){\epsilon }_t\mathrm{,\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\text{for}\mathrm{<mi>\; </mi>}t=\mathrm{1,}\cdots \mathrm{,}n$ (13)

where $y_t$ is the time series at time t, ${\mu }_0$ is the unconditional mean of the process. We assume the noise process ${\epsilon }_t$ to be Gaussian, with expectation zero and variance ${\sigma }_{\epsilon }^2$ .

To allow for a mean level shift, after time $t=i,\mathrm{<mi>\; </mi>}i=2,\cdots ,n$ of the data, we write the sum of an unobserved ARFIMA process and the term for the mean level shift which we will denote as LS-ARFIMA(p, d, q)

$y_t={\mu }_0+{\varphi }^{-1}\left(B\right){\left(1-B\right)}^{-d}\theta \left(B\right){\epsilon }_t+{\mu }_1{\left(1-B\right)}^{-1}{I}_t$ (14)

where $I_t$ is an indicator variable taking values 1 for $t=i$ , and 0 otherwise. The parameter ${\mu }_1$ indicates the size of the mean level shift at time $t=i$ . The mean level shift is an abrupt but permanent shift by ${\mu }_1$ in the series caused by an intervention.

The extension of (14) to k level shifts is straightforward. We define ${\mu }_j$ as the j^th shift in level, compared to the previous level, where $j=\mathrm{1,}\cdots \mathrm{,}k$ . When we allow k level changes at pre-specified time $t=j$ , we can extend (14) to

$y_t={\mu }_0+{\varphi }^{-1}\left(B\right){\left(1-B\right)}^{-d}\theta \left(B\right){\epsilon }_t+{\displaystyle \underset{j=1}{\overset{k}{\sum }}}{\mu }_j{\left(1-B\right)}^{-1}{I}_t$ (15)

The component ${\displaystyle {\sum }_{j=1}^k}{\mu }_j{\left(1-B\right)}^{-1}{I}_t$ allows the intercept of the ARFIMA model to fluctuate over time between ${\mu }_0$ and ${\mu }_0+{\displaystyle {\sum }_{j=1}^k}{\mu }_j$ .

3.2. The GARCH(r, s) Model with Level Shift

As indicated earlier, [4] introduced the GARCH(r, s) model which defines the conditional variance equation as follows:

$h_t={\omega }_0+{\displaystyle \underset{i=1}{\overset{r}{\sum }}}{\alpha }_i{\epsilon }_{t-i}^2+{\displaystyle \underset{i=1}{\overset{s}{\sum }}}{\beta }_i{h}_{t-i}$ (16)

To allow for a volatility level shift, denoted ${\alpha }_1$ , after time $t=i,\mathrm{<mi>\; </mi>}i=2,\cdots ,n$ of the data, we write $h_t$ as the sum of an unobserved GARCH process and the term of the volatility level shift which we will denote as LS-GARCH(r, s).

$h_t={\omega }_0+{\displaystyle \underset{i=1}{\overset{r}{\sum }}}{\alpha }_i{\epsilon }_{t-i}^2+{\displaystyle \underset{i=1}{\overset{s}{\sum }}}{\beta }_i{h}_{t-i}+{\omega }_1{\left(1-B\right)}^{-1}{I}_t$ (17)

where $I_t$ is an indicator variable taking values 1 for $t=i$ , and 0 otherwise. The parameter ${\omega }_1$ indicates the size of the volatility level shift at time $t=i$ .

The extension of (17) to k volatility level shifts is straightforward. We define ${\omega }_j$ as the j^th shift in volatility level, compared to the previous level, where $j=\mathrm{1,}\cdots \mathrm{,}k$ . When we allow k volatility level changes at pre-specified time $t=j$ , we can extend (17) to

$h_t={\omega }_0+{\displaystyle \underset{i=1}{\overset{r}{\sum }}}{\alpha }_i{\epsilon }_{t-i}^2+{\displaystyle \underset{i=1}{\overset{s}{\sum }}}{\beta }_i{h}_{t-i}+{\displaystyle \underset{j=1}{\overset{k}{\sum }}}{\omega }_j{\left(1-B\right)}^{-1}{I}_{t_j}$ (18)

The component ${\displaystyle {\sum }_{j=1}^k}{\omega }_j{\left(1-B\right)}^{-1}{I}_{t_j}$ governs the level shift movement of GARCH model intercept, that is baseline volatility, over time between ${\omega }_0$ and ${\omega }_0+{\displaystyle {\sum }_{j=1}^k}{\omega }_j$ .

3.3. The General ARFIMA(p, d, q)-GARCH(r, s) Model with Level Shift

Extension of the ARFIMA(p, d, q)-GARCH(r, s) model to the case with level shift is given by the following equation which we will denote as LS-ARFIMA-LS-GARCH

$\begin{array}{l}{y}_t={\mu }_0+{\varphi }^{-1}\left(B\right){\left(1-B\right)}^{-d}\theta \left(B\right){\epsilon }_t+{\displaystyle \underset{j=1}{\overset{k}{\sum }}}{\mu }_j{\left(1-B\right)}^{-1}{I}_t\\ {\epsilon }_t=z_t\sqrt{h_t},\mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}{\epsilon }_t|F_{t-1}~N\left(0,h_t\right)\\ h_t={\omega }_0+{\displaystyle \underset{i=1}{\overset{r}{\sum }}}{\alpha }_i{\epsilon }_{t-i}^2+{\displaystyle \underset{i=1}{\overset{s}{\sum }}}{\beta }_i{h}_{t-i}+{\displaystyle \underset{j=1}{\overset{k}{\sum }}}{\omega }_j{\left(1-B\right)}^{-1}{I}_t\end{array}$ (19)

The LS-ARFIMA-LS-GARCH series is shown in Figure 1.

4. Estimation of LS-ARFIMA-LS-GARCH Model Parameters

4.1. Estimation of LS-ARFIMA Model Parameters

The first step of estimation consists in estimating the ARFIMA(p, d, q) assuming that the conditional variance is constant over time. By rearranging Equation (14) for one mean level shift we have:

$\varphi \left(B\right){\left(1-B\right)}^d{y}_t={\mu }_0+\theta \left(B\right){\epsilon }_t+{\mu }_1{\left(1-B\right)}^{-1}{I}_t\mathrm{.}$ (20)

Therefore the null hypothesis of unconditional mean constancy becomes: $H_0\mathrm{<mo>\; :\; </mo>}{\mu }_1=0$ . Let ${\psi }_1={\left(d\mathrm{,}{\mu }_0\mathrm{,}{\mu }_1\mathrm{,}{\varphi }^{\prime }\mathrm{,}{\theta }^{\prime }\mathrm{,}{\sigma }^2\right)}^{\prime }$ be the approximate likelihood estimator (MLE) ${\hat{\psi }}_1$ of ${\psi }_1$ that maximizes the conditional log-likelihood:

(21)

The partial derivatives evaluated under are given by:

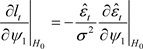(22)

Figure 1. ARFIMA-GARCH time series with level shift effect.

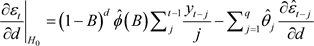
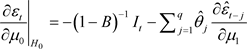
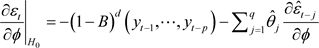
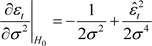
4.2. Estimation of LS-GARCH Parameters

Once the LS-ARFIMA model is estimated and the residuals 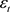are obtained, we test the alternative of LS-GARCH specification with one volatility level shift against the null hypothesis of GARCH model. Let us rearrange model (17) with one volatility level shift:

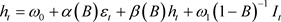(23)

Therefore the null hypothesis of the unconditional variance constancy becomes:. Let be the vector of the LS-GARCH model parameters and the quasi-likelihood function is given by:

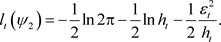(24)

The partial derivatives evaluated under are given by:

(25)

Under the null hypothesis, the “hats” indicates the maximum likelihood estimator and denotes the conditional variance estimated at time t.

5. Level Shift Detection in ARFIMA-GARCH

5.1. Mean Level Shift Detection in ARFIMA-GARCH

The mean level shift detection test was previously derived by [25] for ARFIMA(p, d, q) models assuming conditional variance is constant over time. For our purpose a natural extension of the level shift detection test of the mean for a realization of time series satisfying LS-ARFIMA-LS-GARCH model was proposed. In order to derive the test statistic, let us rewrite model (15), with only one mean level change:

(26)

The hypothesis to be tested is

(27)

which is based on a realization of time series satisfying ARFIMA-GARCH model with mean level shift.

Extension of [26] test statistics can be written as:

(28)

where is the estimated intervention or impact at time and is the sample mean of a time series and is an estimate of the standard error of.

Model (26) can be rewritten as:

This implies transforming the series by differencing once. Thus if,. The intervention parameter can be estimated using various methods like the maximum likelihood estimation and least square estimation. The least square estimate of if the mean intervention is at time is given by

(29)

The distribution of the statistics is discussed in great detail in [25] for ARFIMA(p, d, q) assuming conditional variance is constant over time. This is based on the fact that it is originally normally distributed and then transformed to the Gamma distribution both of which belong to the Domain of Attraction of the Gumbel distribution with normalizing constants:

1) Normal Distribution:

(30)

2) Gamma Distribution:

(31)

The maximum domain of attraction of the Gumbel is shown to some extent in [27] and in greater detail in [28].

Let be a time series satisfying the level shift model

(32)

Assume that the stationary component of the model is a Gaussian time series with mean zero and autocovariance function such that

(33)

Let also the test statistics be given by

(34)

Then under, the statistics satisfies

(35)

where D signifies convergence in distribution. Here, is location parameter and is scale parameter. The location parameter is also the mode of the distribution. Inverse of the in Equation (35), is given by:

(36)

Thus a test of hypothesis can be conducted by comparing the test statistic in Equation (34) with an appropriate critical value. The largest statistic is considered an intervention at the significance if the value exceeds the critical value.

5.2. Volatility Level Shift Detection in ARFIMA-GARCH Model

The second step is a natural extension of mean level shift detection in ARFIMA-GARCH model to volatility level shift detection in ARFMA-GARCH model. After estimating the LS-ARFIMA model and the residuals are obtained, we test, the alternative hypothesis of LS-GARCH volatility level shift against the null hypothesis of GARCH model. Let us rewrite model (18) with one volatility level shift:

(37)

The hypothesis tested is

(38)

which is based on a realization of time series from a GARCH model with level shift.

The derivation is based on the statistics

(39)

where is the estimated intervention or impact at time

and is the sample mean of a time series of unconditional variance. is an estimate of the standard error of.

Model (37) can be rewritten as

(40)

Thus if,. The intervention parameter can be estimated using various methods like the maximum likelihood estimation and least square estimation. The least square estimate of if the volatility intervention is at time is

(41)

Thus from Equation (12),.

Similarly just like the mean level shift test statistic, the distribution of the statistics is based on the fact that it is originally normally distributed and then transformed to the Gamma distribution both of which belong to the Domain of Attraction of the Gumbel distribution with normalizing constants:

1) Normal Distribution:

(42)

2) Gamma Distribution:

(43)

The maximum domain of attraction of the Gumbel is shown to some extent in [27] and in greater detail in [28].

Let be a time series satisfying the volatility level shift model

(44)

For any realization of this time series, let

(45)

Then under, the statistics satisfies

(46)

where D signifies convergence in distribution. Thus a test of hypothesis can be conducted by comparing the test statistic Equation (45) with an appropriate critical value. The largest statistic is considered as volatility intervention at the level of significance if the test statistic value exceeds the critical value.

5.3. Mean and Volatility Level Shift Detection in ARFIMA-GARCH

Summary of the detection procedure is presented below:

1) Plot the data to get a picture of the type of series and possible level shift in the data.

2) Assume that the underlying ARFIMA-GARCH series contains no level shift and use maximum likelihood procedure to estimate its parameters.

3) The first test is performed to check the mean level shift which can be conducted as follows:

a) State the hypothesis being tested, which is

(47)

b) Compute the residuals, the impact and the test statistics like the popular [26] ’s likelihood ratio test statistics given by

where is the estimated intervention or impact at time, is an estimate of the standard error of. Then compute the statistics:

c) Determine the critical values to use in the test.

d) Determine whether observations are level shifts and remove each from the series by subtracting the value of the impact then apply the ARFIMA-GARCH modeling procedure to obtain the adequate model.

4) The second test is performed to check the volatility level shift which can be conducted as follows:

a) State the hypothesis being tested, which is

(48)

b) Compute the residuals, the impact and the test statistics like the popular [26] ’s likelihood ratio test statistics given by

where is the estimated volatility intervention or impact at time,

is an estimate of the standard error of. Then compute the statistics:

c) Determine the critical values to use in the test.

d) Determine whether observations are level shifts and remove each from the series by subtracting the value of the impact then apply the ARFIMA-GARCH modeling procedure to obtain the adequate model.

6. Simulation Study of the Level Shift Detection Procedure

To appreciate the procedure we derived a simulation study consisting of simulation of critical values for mean and volatility level shift, simulating different sizes of mean and volatility level shift impact, performing detection test and conducting the power of the mean level shift detection procedure.

6.1. Critical Values for Mean Level Shift Detection Test

Simulation of the critical values was done using R software. An assumption that there are mean level shifts was made, then simulations conducted. This is based on an estimate of the statistic as shown in Equation (34) with norming constants given in Equation (31).

The critical values for the 10%, 5% and 1% level of significance are presented in Table 2. As the sample size n, increases, the critical values converges. It can also be observed that for different values of long memory parameter the critical values varies but not significantly. For anti-pesistent parameter the critical values are the same, they only increase with the sample size n as depicted in Table 3. Samples of sizes 100, 500, 1,000, 5,000, 10,000, 20,000 and 50,000 were used. It can be noted that, for example, at 5% level of significance with the critical value ranges from 4.0390 for a sample of size 100 to 5.1190 for a sample of size 50,000. Similarly at 5% level of significance with, the critical value ranges from 4.1342 for a sample of size 100 to 4.9377 for a sample of size 50,000. We can conclude without loss of generality that at 5% level of significance the critical value converges to a Gumbel critical value of 5.1702, given in Equation (35) with and as the sample size increases. Using and, the 10% and 1% level of significance for the Gumbel critical values are 4.4504 and 6.8001 respectively. The simulated critical values in Table 2 can be observed to be converging to Gumbel critical values as the sample size increases.

Table 2. Critical values for mean level shifts using (, , , , and).

Table 3. Critical values for mean level shifts using (, , , , and).

Figure 2 shows the graph of critical values for detecting mean level shift using 5% level of significance. It can be depicted from the graph that the critical values depend on the fractional differencing parameter d and sample size. As the sample size increases the critical value appears to be converging. The same scenario is also the case for 1% and 10% level of significance.

6.2. Mean Level Shift Detection Test

Before conducting the test it should be clear that the position of the mean level shift impact i.e. point is not known. The level shift impact is tested for significance using the hypotheses versus. An observation corresponding to the maximum is considered a level shift at level of significance if the statistic exceeds the critical value for given d and sample size n.

For illustration purposes, mean level shift of sizes and are introduced in an ARFIMA-GARCH(1, 0.2, 1) (1, 1) time series model with, , , and sample size of with intervention at point using R program. The resulting test statistics that occurs at point 4,999 due to differencing are and respectively. These are greater than the critical values 3.7579, 4.5000 and 6.2892 at and 1% level of significance respectively, implying the rejection of at all level of significance.

6.3. Power of the Mean Level Shift Detection Test

The probability of correctly detecting a mean level shift is the power of the test. Table 4 shows the frequency (denoted Freq) with which the location of a mean level shift is correctly detected, the probability (denoted Prob) of correctly detecting the mean level shift in the form of the statistics. Power of the mean level shift detection test involves samples of size n, different mean level shift impact’s, 95% Gumbel critical value of 5.1348. The underlying model used is ARFIMA(1, d, 1)-GARCH(1, 1) with, , , , , for 10,000 replications.

Figure 2. Critical value (5%) for detecting mean level shift.

Table 4. Power of the mean level shift detection test using (, , , , , , and 95% Gumbel critical value of 5.1348).

Table 4 depicts the probability of correctly detecting a mean level shift is high as long as the mean level shift is significantly different from the 95% Gumbel critical value of 5.1348 but it is low as long as the resulting level shift is low. The frequencies of the detection of mean level shift approaches 10 000 as the size of mean level shift increases.

Figure 3 is a graph showing the power of the detection test of mean level shift using 95% Gumbel critical value of 5.1348. This is the general behaviour for 90% and 99% Gumbel critical value.

6.4. Critical Values for Volatility Level Shift Detection Test

As with critical values for the mean level shift, similar simulation of the critical values for the volatility level shift was done using R programs. An assumption that there are volatility level shifts was made, then simulations conducted. This is based on an estimate of the statistic as shown in Equation (45) with norming constants given in Equation (43).

The critical values for the 10%, 5% and 1% level of significance are presented in Table 5. As the sample size n, increases, the critical values slowly converges. It can also be observed that for different values of long memory parameter the critical values varies but not significantly. For anti-pesistent parameter the critical values are the same, they only increase with the sample size n as depicted in Table 6. Samples of sizes 100, 500, 1,000, 5,000, 10,000, 20,000 and 50,000 were used. It can be noted that, for example, at 5% level of significance with the critical value ranges from 5.8953 for a sample of size 100 to 67.6419 for a sample of size 50,000. We can conclude without loss of generality that the simulated critical values in Table 5 can be observed to be diverging critical values as the sample size increases.

Figure 4 shows the graph of critical values for detecting volatility level shift using 5% level of significance. Unlike the mean level shift, it can be depicted from the graph that the critical values do not depend on the fractional differencing parameter d. But as the sample size increases the critical value appears to be diverging. The same scenario is also the case for 1% and 10% level of significance.

Figure 3. Power of the level shift detection procedure.

Table 5. Critical values for volatility level shifts using (, , , , and).

Table 6. Critical values for volatility level shifts using (, , , , and).

Figure 4. Critical value (5%) for detecting volatility level shift.

6.5. Volatility Level Shift Detection Test

Before conducting the volatility level shift test it should be clear that the position of the volatility level shift impact i.e. point is not known. The volatility level shift impact is tested for significance using the hypotheses versus. An observation corresponding to the maximum is considered a volatility level shift at level of significance if the statistic exceeds the critical value for a given fractional differencing d and a sample size n.

For illustration purposes, volatility level shift of sizes and are introduced in an ARFIMA-GARCH(1, 0.2, 1) (1, 1) time series model with, , , and of at point using R program. The resulting test statistic occurring at point 4 999 due to differencing are and respectively. These are greater than the critical values 28.9583, 37.8952 and 68.0323 at and 1% level of significance respectively, implying the rejection of at all level of significance.

7. Conclusions

In this study, we derive and extend level shift detection test to the case of ARFIMA-GARCH models, the resulting models were denoted as LS-ARFIMA-LS-GARCH models. The derivation was in both the mean and volatility, such that a natural extension to LS-ARFIMA-LS-GARCH models was established. Then parameter estimation of LS-ARFIMA-LS-GARCH models was derived. Step by step detection procedure for level shift was also suggested and presented. Finally a simulation study of the critical values was performed using sample sizes of up-to 50 000 for mean level shift detection test and up to 100 000 for volatility level shift detection test. Some concluding remarks can be summarized as follows:

1) A natural extension of level shift models in ARFIMA-GARCH models (denoted LS-ARFIMA-LS-GARCH models) was established.

2) Level shift detection tests for both the mean and volatility in models with ARFIMA-GARCH using step by step procedure were established.

3) Parameter estimation of LS-ARFIMA-LS-GARCH models was derived using quasi-maximum likehood estimation.

4) The simulation study shows that critical values of the mean level shift detection test converges to Gumbel whereas the critical values of volatility level shift detection test diverge.

5) Power of the test was also conducted and results for mean level shift shows that the probability of correctly detecting a mean level shift is high as long as the mean level shift impact is significantly different from the 95% Gumbel critical values of 5.1348.

6) It was observed that critical values of volatility level shift detection procedure fail to converge to a Gumbel distribution. Further derivation and establishment of the normalizing constants of the test statistics and distribution which converges is still work in progress.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Granger, C.W.J. and Joyeux, R. (1980) An Introduction to Long-Memory Time Series Models and Fractional Differencing. Journal of Time Series Analysis, 1, 15-29. https://doi.org/10.1111/j.1467-9892.1980.tb00297.x
[2]	Hosking, J.R.M. (1981) Fractional Differencing. Biometrika, 68, 165-176. https://doi.org/10.1093/biomet/68.1.165
[3]	Robinson, P.M. and Zaffaroni, P. (1998) Nonlinear Time Series with Long Memory: A Model for Stochastic Volatility. Journal of Statistical Planning and Inference, 68, 359-371. https://doi.org/10.1016/S0378-3758(97)00149-3
[4]	Bollerslev, T. (1986) Generalized Autoregressive Conditional Heteroskedasticity. Journal of Econometrics, 31, 307-327. https://doi.org/10.1016/0304-4076(86)90063-1
[5]	Bollerslev, T., Engle, R.F. and Wooldridge, J.M. (1988) A Capital Asset Pricing Model with Time-Varying Covariances. Journal of Political Economy, 96, 116-131. https://doi.org/10.1086/261527
[6]	Weiss, A.A. (1984) ARMA Models with ARCH Errors. Journal of Time Series Analysis, 5, 129-143. https://doi.org/10.1111/j.1467-9892.1984.tb00382.x
[7]	Ling, S.Q. and Li, W.K. (1997) On Fractionally Integrated Autoregressive Moving-Average Time Series Models with Conditional Heteroscedasticity. Journal of the American Statistical Association, 92, 1184-1194. https://doi.org/10.1080/01621459.1997.10474076
[8]	Reisen, V.A., Sarnaglia, A.J.Q., Reis Jr., N.C., Levy-Leduc, C. and Santos, J.M. (2014) Modeling and Forecasting Daily Average PM10 Concentrations by a Seasonal Long-Memory Model with Volatility. Environmental Modelling & Software, 51, 286-295. https://doi.org/10.1016/j.envsoft.2013.09.027
[9]	Tong, H. (2011) Nonlinear Time Series Analysis. In: Lovric, M., Ed., International Encyclopedia of Statistical Science, Springer, Berlin, Heidelberg, 955-958. https://doi.org/10.1007/978-3-642-04898-2_411
[10]	Narayan, P.K., Liu, R.P. and Westerlund, J. (2016) A GARCH Model for Testing Market Efficiency. Journal of International Financial Markets, Institutions and Money, 41, 121-138. https://doi.org/10.1016/j.intfin.2015.12.008
[11]	Box, G.E.P., Jenkins, G.M., Reinsel, G.C. and Ljung, G.M. (2015) Time Series Analysis: Forecasting and Control. John Wiley & Sons, Hoboken.
[12]	Adenstedt, R.K. (1974) On Large-Sample Estimation for the Mean of a Stationary Random Sequence. The Annals of Statistics, 2, 1095-1107. https://doi.org/10.1214/aos/1176342867
[13]	Beran, J. (2017) Statistics for Long-Memory Processes. Routledge, Abingdon-on-Thames. https://doi.org/10.1201/9780203738481
[14]	Baillie, R.T., Bollerslev, T. and Mikkelsen, H.O. (1996) Fractionally Integrated Generalized Autoregressive Conditional Heteroskedasticity. Journal of Econometrics, 74, 3-30. https://doi.org/10.1016/S0304-4076(95)01749-6
[15]	Robinson, P.M. (2003) Long Memory Time Series. In: Robinson, P.M., Ed., Time Series with Long Memory, Oxford University Press, Oxford, 4-32.
[16]	Engle, R.F. (1982) Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica: Journal of the Econometric Society, 50, 987-1007. https://doi.org/10.2307/1912773
[17]	Bollerslev, T., Engle, R.F. and Nelson, D.B. (1994) Arch Models. In: Engle, R.F. and McFadden, D.L., Eds., Handbook of Econometrics, Vol. 4, Elsevier, Amsterdam, 2959-3038. https://doi.org/10.1016/S1573-4412(05)80018-2
[18]	Baillie, R.T., Chung, C.-F. and Tieslau, M.A. (1996) Analysing Inflation by the Fractionally Integrated ARFIMA-GARCH Model. Journal of Applied Econometrics, 11, 23-40. https://doi.org/10.1002/(SICI)1099-1255(199601)11:1<23::AID-JAE374>3.0.CO;2-M
[19]	Montanari, A., Rosso, R. and Taqqu, M.S. (2000) A Seasonal Fractional ARIMA Model Applied to the Nile River Monthly Flows at Aswan. Water Resources Research, 36, 1249-1259. https://doi.org/10.1029/2000WR900012
[20]	Giraitis, L. and Leipus, R. (1995) A Generalized Fractionally Differencing Approach in Long-Memory Modeling. Lithuanian Mathematical Journal, 35, 53-65. https://doi.org/10.1007/BF02337754
[21]	Yang, Q. and Wang, Y.S. (2019) Application of the Improved Generalized Autoregressive Conditional Heteroskedast Model Based on the Autoregressive Integrated Moving Average Model in Data Analysis. Open Journal of Statistics, 9, 543-554. https://doi.org/10.4236/ojs.2019.95036
[22]	Bisognin, C. and Lopes, S.R.C. (2009) Properties of Seasonal Long Memory Processes. Mathematical and Computer Modelling, 49, 1837-1851. https://doi.org/10.1016/j.mcm.2008.12.003
[23]	Ishida, I. and Engle, R.F. (2002) Modeling Variance of Variance: The Square Root, the Affine, and the CEV GARCH Models. Working Papers, Dept. Finances, New York.
[24]	Belkhouja, M. and Mootamri, I. (2016) Long Memory and Structural Change in the g7 Inflation Dynamics. Economic Modelling, 54, 450-462. https://doi.org/10.1016/j.econmod.2016.01.021
[25]	Chareka, P., Matarise, F. and Turner, R. (2006) A Test for Additive Outliers Applicable to Long Memory Time Series. Journal of Economic Dynamics and Control, 30, 595-621. https://doi.org/10.1016/j.jedc.2005.01.003
[26]	Chang, I., Tiao, G.C. and Chen, C. (1988) Estimation of Time Series Parameters in the Presence of Outliers. Technometrics, 30, 193-204. https://doi.org/10.1080/00401706.1988.10488367
[27]	Leadbetter, M.R., Lindgren, G. and Rootzen, H. (1983) Extreme and Related Properties of Random Sequence and Processes. Springer-Verlag, New York.
[28]	Embrechts, P., Klppelberg, C. and Mikosch, T. (1997) Modeling Extremal Events for Insurance and Finance. Springer-Verlag, Berlin. https://doi.org/10.1007/978-3-642-33483-2