A Brief New Proof to Fermat’s Last Theorem and Its Generalization

Demetrius Chr. Poulkas^1,2,3,4

¹Department of Mathematics of Aristotle University of Thessaloniki, Thessaloniki, Greece.
²School of the Faculty of Engineering of Aristotle University of Thessaloniki, Thessaloniki, Greece.
³School of Electrical and Computer Engineering of National Technical University of Athens, Athens, Greece.
⁴Department of Mechanical Engineering and Aeronautics of Faculty of Engineering of University of Patras, Patra, Greece.

DOI: 10.4236/jamp.2020.84053                

Abstract

This article presents a brief and new solution to the problem known as the “Fermat’s Last Theorem”. It is achieved without the use of abstract algebra elements or elements from other fields of modern mathematics of the twentieth century. For this reason it can be easily understood by any mathematician or by anyone who knows basic mathematics. The important thing is that the above “theorem” is generalized. Thus, this generalization is essentially a new theorem in the field of number theory.

Keywords

Brief Proof of Fermat’s Last Theorem, Unsolved Mathematical Problems, Fermat’s Last Theorem, Generalization of the Fermat’s Last Theorem, Prime Number Problems, Millennium Problems

1. Introduction

Fermat’s last theorem (known historically by this title) has been an unsolved puzzle in mathematics for over three centuries. The theorem itself is a deceptively simple formulation in mathematics, while Fermat famously stated that the problem had been solved around 1637. His claim was discovered 30 years after his death, as a clear statement on the margin of a book, but Fermat died without leaving any evidence as to his claim. This claim eventually became one of the most famous unsolved problems of mathematics. Efforts made to prove it, led to substantial development in number theory, and over time Fermat’s Last Theorem gained legendary prominence as one of the most popular unsolved problems in mathematics [1] - [8].

Because this problem is easily understood by everyone (in terms of its wording), most incorrect proofs have been created from time to time of any other problem in the history of mathematics.

The “Fermat’s last theorem” was made known to me, before it is solved by Professor Andrew Wiles [9]. The problem impressed me and I recorded it in my memory. Later, for several years I never tried to solve it. But, because in all those years never did I stop solving problems from International Mathematical Olympiad (IMO) or finding solutions to unsolved problems of Number Theory, at some time I thought about trying to solve Fermat’s last theorem, believing it could have a brief solution. This was done eleven years ago. One morning while I was at my desk, I pulled it out in the surface from my memory and within a short time, when, I start to analyze the problem, I devised the double inequality (1.5) and at that moment with a great enthusiasm I exclaimed (like Archimedes) that I solved the “Fermat’s last theorem”.

Double inequalities (1.5) and (2.5) are the keys to the solutions I present to you. Also, very important are the conditions (1.7) and (1.14) for the classical theorem and (2.10) and (2.19) respectively for the general theorem. First I completed the solution at the classical problem. This solution, led me to generalize the problem.

2. A Brief New Proof to Fermat’s Last Theorem

Fermat’s last theorem (classical problem)

If x, y, z are positive integers that differ from each other, then the following equation:

(where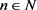,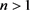) (1.1)

when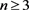, have no positive integer solutions.

Proof of Theorem

We consider positive integers x, y, z that differ from each other and hypothesize that they verify the Equation (1.1) for a natural number. Also, we hypothesize, without loss of the generality, that:

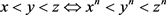(1.2)

Taking into account the Equation (1.1) and the condition (1.2), on the basis of the above hypothesis, we have:

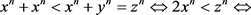
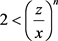(1.3)

Also, is: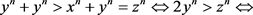

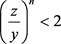(1.4)

By combining conditions (1.3) and (1.4) we have:

(1.5)

Comment: The double inequality (1.5) is sufficient but not necessary, i.e. the converse is not always the case. For example, we consider that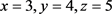

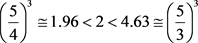and. We have, and.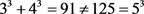

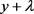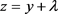If we substitute z with or, where 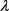is a positive integer, then for the positive integers x, y, z, which according to the hypothesis we originally made, verify the Equation (1.1) for a natural number, it is true that:

(1.6)

We will prove that when the positive integers x, y, z verify the Equation (1.1) for a natural number, the number x is greater than the number λ or.

Indeed from Equation (1.6) we have:

or

(1.7)

So, given the above we have:

(1.8)

We distinguish the following cases:

Α.

We have:

(1.9)

Considering Bernoulli’s inequality is (for):

(1.10)

By combining the conditions (1.9) and (1.10) we have:

(1.11)

Because of condition (1.11) we observe that condition (1.5) is not satisfied, so in this case Equation (1.1) has no positive integer solutions.

Β.

Since in case A. Equation (1.1) does not have positive integer solutions, obviously if they exist, this will be in case B, when the condition is applied. So, we have:

(1.12)

We will then prove that when positive integers x, y, z verify the Equation (1.1) for a natural number, the number λ is less than the difference or:. From condition (1.8) we have: {,}. By adding the members of the above inequalities and deleting x, also we have:. It remains to be seen whether the equation holds. This equality is true when the following condition applies:

* (1.13)

*Is, (and) or or. The first condition is rejected because (not acceptable), from the second condition we have, so.

Combining the Equation (1.6) and Equation (1.13) we have:

. This is an absurd, because a rational number cannot be equal to an integer**.

**The number, is a rational number because for.

Therefore, when Equation (1.1) verified, it is true that:

(1.14)

Given the condition (1.14), we have:

(1.15)

Based on condition (1.15), we distinguish the following sub cases:

Β₁.

We have: (because) (due to (1.12)) we have: or. Equation (1.1) has positive integer solutions when or. So,. While on the contrary, the Equation (1.1) has no positive integer solutions when or. So,.

Β₂.

We have: (because) (due to (1.12), we have: *** or. So we’re being led to the same conclusion as Β₁.

***The inequality, was written this way with the following reasoning: We hypothesize it’s and we have: (∀) or regardless from the exponent n. Then considering

the conditions and, because the number λ is greater or equal than number one for all n or, $\forall n>1$, we have:

- $y>\lambda n$ $\iff$ $\frac{\lambda }{y}<\frac{1}{n}$ or $\frac{1}{y}\le \frac{\lambda }{y}<\frac{1}{n}$ or $\frac{1}{y}<\frac{1}{n}$

- $\lambda <y-2$ or $y>\lambda +2\ge 1+2=3$ or $y>3$ $\iff$ $\frac{1}{y}<\frac{1}{3}$

On the basis of inequalities and, we distinguish the following conditions: $\frac{1}{y}<\frac{1}{3}<\frac{1}{n}$ and. We observe that for the first

condition is satisfied while the second condition is not satisfied, on the contrary for, the second condition is satisfied while the first condition is not satisfied. Therefore, there is always at least one natural number n greater than the

number one or, so that, the condition $\frac{1}{y}<\frac{1}{3}<\frac{1}{n}$ or is not

satisfied. This means that the Equation (1.1) is not verified always for every natural number and this is contrary to the sentence “when regardless from the exponent n, the Equation (1.1) has solution for every natural

number” which arises from the hypothesis that, according to the logic by which the solution of the problem was structured, in this paper. This is an absurd and that is why inequality is rejected. Therefore we consider the inequality is acceptable and so we ended up in the inequality. (For a different reasoning, for the same, see in Annex)

Conclusion 1: From the above it is concluded that Equation (1.1), when have positive integer solutions, whereas when does not have positive integer solutions. In the second case, Fermat’s last theorem is verified.

3. New Theorem

“Generalization of the ‘Fermat’s last theorem’’

If are positive integers that differ from each other (m finite number), then for the following equation:

, (where,) (2.1)

when, have no integer solutions. For, , Fermat’s last theorem occurs.

Proof of Theorem

We consider positive integers that differ from each other (m finite number) and hypothesize that they verify Equation (2.1) for a natural number. Also, we hypothesize, without loss of the generality, that:

(2.2)

Taking into account Equation (2.1) and the condition (2.2), on the basis of the above hypothesis we have:

or

(2.3)

Also, or

(2.4)

By combining conditions (2.3) and (2.4) we have:

(2.5)

Comment: The double inequality (2.5) is sufficient but not necessary, i.e. the converse is not always the case. For example we consider that, , , , and. We have,

and.

If we substitute with or, where is a positive integer, for the positive integers, which according to the hypothesis we originally made, verify the Equation (2.1) for a natural number, it is true that:

(2.6)

We distinguish the following cases:

Α.

We have,

(2.7)

Considering Bernoulli’s inequality, it is (for),

(2.8)

By combining the conditions (2.7) and (2.8) we have,

(2.9)

Because of condition (2.9), we observe that double inequality (2.5) is not satisfied, so in this case Equation (2.1) has no positive integer solutions.

Β.

Since in case A. the Equation (2.1) does not have positive integer solutions, obviously if they exist, this will be in case B, when the condition is applied. So, we have:

(2.10)

We will then prove that when positive integers verify the Equation (2.1) for a natural number, the number λ is less than the difference or.

1) First, we consider that. Based on this condition, we have:

(2.11)

From condition (2.11) we have, {, , , , }. By adding the members of the above inequalities and making all deletions, also we have:. It remains to be seen whether the equation holds. This equality is true when the following condition applies:

* (2.12)

*It is proved in the same way, as previously proved the condition (1.17) (see Annex).

First way: If, taking into account the condition (2.12) we have: (and) or (and) or (and) or or. This is an absurd, because, so be.

Second way: If, combining (2.6) and (2.12) we have:

(2.13)

By applying mathematical induction we have:

- For, from (2.12) we have: , this is an absurd, because a rational number cannot be equal to an integer.

So, for,.

- For, we hypothesize that is true the following condition:

(2.14)

- We will prove and for is true that:

(2.15)

Combining the conditions (2.14) and (2.15) we have,

Suffice it to prove that: or

or

or or, () (2.16)

If, (true, so the condition (2.16) also is true and consequently and the condition (2.15)). So, must be.

2) Second, we consider that or,.

First way: Based on the immediately above condition we have: {, , , }. By adding the members of the above inequalities and making all deletions, we have:

or (2.17)

Hypothesizing that: because from (2.17) is also we have: or . This is true due to (2.17), therefore, . It remains to be seen whether the equation holds. This equality is true when the following condition applies:

** (2.18)

**The condition (2.18) proves on the same way as the condition (2.12) (see Annex).

So, if and into taking account the condition (2.18) is: or, where. Given the previous conditions, we have: or (and) or. This is an absurd, because. So must be.

Second way: From condition (2.17) is: or. Hypothesizing that: and into taking account the previous condition we have: or. This is an absurd, because, so must be.

Note: The proof that, can be done and by applying mathematical induction (see Annex). Also, is always (see Annex).

Thus, in all cases, when the Equation (2.1) is verified for a natural number, it is true that:

(2.19)

Given condition (2.19) we have:

(2.20)

Based on condition (2.20) we distinguish the following sub cases:

Β₁.

We have: (if, or) (due to (2.10)) we have: or

(2.21)

Based on condition (2.21) we have: Equation (2.1) has positive integer solutions when or. So,. While on the contrary, the Equation (1.1) has no positive integer solutions when or. So,.

Β₂.

We have: (if, or) (due to (2.10)) we have: *** or . So we’re being led to the same conclusion as Β₁.

***The inequality, was written this way with the following reasoning: We hypothesize it’s and we have: (if and is) or. Also if or, because is, we observe that if or, is true that. Therefore, if the number λ is greater or equal than number one or $\lambda \ge 1$ for all n, m. Then considering the conditions $x_{m-1}>\frac{n}{m-2}\lambda$ and $\lambda <x_{m-1}-\left(m-1\right)$, because $\lambda \ge 1$ for each natural number $n>1$ and every $m\ge 3$, we have:

- $x_{m-1}>\frac{n}{m-2}\lambda$ $\iff$ $\frac{\lambda }{x_{m-1}}<\frac{m-2}{n}$ or $\frac{1}{x_{m-1}}\le \frac{\lambda }{x_{m-1}}<\frac{m-2}{n}$ or $\frac{1}{x_{m-1}}<\frac{m-2}{n}$

- $\lambda <x_{m-1}-\left(m-1\right)$ or $x_{m-1}>\lambda +\left(m-1\right)\ge 1+m-1=m$ or $x_{m-1}>3$ $\iff$ $\frac{1}{x_{m-1}}<\frac{1}{m}$

On the basis of inequalities $\frac{1}{x_{m-1}}<\frac{m-2}{n}$ and $\frac{1}{x_{m-1}}<\frac{1}{m}$ we distinguish the following conditions: $\frac{1}{x_{m-1}}<\frac{1}{m}<\frac{m-2}{n}$ and $\frac{1}{x_{m-1}}<\frac{m-2}{n}\le \frac{1}{m}$. We observe

that for $n<m(m-2)$ the first condition is satisfied while the second condition is not satisfied, on the contrary for $n\ge m(m-2)$, the second condition is satisfied while the first condition is not satisfied. Therefore, there is always at least one natural number n greater than the number one or $n>1$, so that the condition

or $\frac{1}{x_{m-1}}<\frac{m-2}{n}\le \frac{1}{m}$ is not satisfied. This means that the

Equation (2.1) is not verified always for each natural number $n>\text{1}$ and every $m\ge 3$ and this is contrary to the sentence “if $\lambda \ge 1$ regardless from the parameters n, m the Equation (2.1) has solutions for each natural number $n>1$

and every $m\ge 3$ ” which arises from the hypothesis that $\frac{n}{m-2}\lambda \ge \frac{n\left(m-1\right)}{\left(n-m+2\right)}$, according to the logic by which the solution of the problem was structured in this paper. This is an absurd and that is why inequality $\frac{n}{m-2}\lambda \ge \frac{n\left(m-1\right)}{\left(n-m+2\right)}$ is rejected. Therefore we consider the inequality $\frac{n\left(m-1\right)}{\left(n-m+2\right)}>\frac{n}{m-2}\lambda$ is acceptable and so we ended up in inequality $x_{m-1}\ge \frac{n\left(m-1\right)}{\left(n-m+2\right)}>\frac{n}{m-2}\lambda$. (For a different reasoning, for the same, see in the Annex)

Conclusion 2: From the above it is concluded that the Equation (2.1) when $n<m^2-2m$ have integer solutions, whereas when $n\ge m^2-2m$ have no integer solutions. In the second case, for $m=3$, answer to Fermat’s Last Theorem is given.

4. Analysis of Results

1) From condition $n\ge m^2-2m$, if $m=3$ we have: $n\ge 3^2-2\times 3=3$. We observe that solution of “Fermat’s Last Theorem” occurs. This, to me, is a very strong indication that the solution of the generalization of Fermat’s theorem is correct.

2) If ( $n-m+2>0$ or $n-m+2\ge 1$ ), is $n\ge m-1$. In this case we have:

i) If $n\ge m^2-2m$, is $\lambda <\frac{\left(m-1\right)\left(m-2\right)}{n-m+2}\le 1$ and the Equation (2.1) has no positive integer solutions.

ii) Whereas, if $m-1\le n<m^2-2m$, can be $\frac{\left(m-1\right)\left(m-2\right)}{n-m+2}>\lambda \ge 1$ and so, Equation (2.1) can have positive integer solutions.

3) What happens if $n-m+2\le 0$ or $n\le m-2$ or $\frac{n}{m-2}\le 1$ ? In this case we have: $\frac{x_{m-1}}{\lambda }>\frac{x_{m-1}}{x_{m-1}-\left(m-1\right)}>1\ge \frac{n}{m-2}$. We observe that, if $x_1>\lambda \ge 1$ or $\lambda \ge x_1\ge 1$, is $\frac{x_{m-1}}{\lambda }>\frac{x_{m-1}}{x_{m-1}-\left(m-1\right)}>1\ge \frac{n}{m-2}$. So, in this case Equation (2.1) also can have positive integer solutions. For example, if $x_1=3$, $x_2=4$, $x_3=12$, $x_4=13$, $\lambda =1$, $n=2$ and $m=4$. We have, $n-m+2=2-4+2=0$ and $3^2+4^2+{12}^2={13}^2$ and ${\left(\frac{1\text{3}}{1\text{2}}\right)}^2\cong \text{1}\text{.174}<4-1<\text{18}\text{.778}={\left(\frac{13}{3}\right)}^2$.

4) The immediately above example and the example which follows, namely: ${27}^5+{84}^5+{110}^5+{133}^5={144}^5$ [10], are indicative of the correctness of those indicated in steps 3, 2. ii), in this section.

5) Equation (1.1) and Equation (2.1) make sense if $n>1$, because for $n=1$, they have infinite solutions or else always have solutions. Thus, in this case, the assumptions and terms had used in the above solutions do not apply.

6) In Equation (1.1), if $1<n<3$, is $n=2$ and so it has solutions that we known since ancient times as Pythagorean Triads.

7) Below, are presented some solutions of Equation (2.1), have made by prominent researchers, from time to time, of course using always the more times computer. It is easy to find that these solutions are perfectly in line with the general theorem.

Solutions of the Equation (2.1), which have made by prominent researchers:

${30}^4+{120}^4+{272}^4+{315}^4={353}^4$ (R. Norrie, 1911),

$7^5+{43}^5+{57}^5+{80}^5+{100}^5={107}^5$ (Sastry, 1934, third smallest),

${27}^5+{84}^5+{110}^5+{133}^5={144}^5$ (Lander & Parkin, 1966),

${19}^5+{43}^5+{46}^5+{47}^5+{67}^5={72}^5$ (Lander, Parkin, Selfridge, smallest, 1967),

${2682440}^4+{15365639}^4+{18796760}^4={20615673}^4$ (Noam Elkies 1986),

${95800}^4+{217519}^4+{414560}^4={422481}^4$ (R. Frye, 1988),

${127}^7+{258}^7+{266}^7+{413}^7+{430}^7+{439}^7+{525}^7={568}^7$ (M. Dodrill, 1999),

${90}^8+{223}^8+{478}^8+{524}^8+{748}^8+{1088}^8+{1190}^8+{1324}^8={1409}^8$ (S. Chase, 2000),

${55}^5+{3183}^5+{28969}^5+{85282}^5={85359}^5$ (Frye, 2004).

5. General Conclusion

The new solution to Fermat’s Last Theorem, which presented here, is as brief and simple as its wording. It is achieved without the use of abstract algebra or elements from other fields of modern mathematics of the twentieth century. For this reason, it can be easily understood by any mathematician or by anyone who knows basic mathematics. This means that it has pedagogical value. At the same time, it is important, that the above “theorem” is generalized to an arbitrarily large number of variables. This generalization is essentially a new theorem in the field of the number theory, very useful to researchers of that field, because it gives answers to many open problems of the number theory. Also, it is important, that the solutions which were found by many prominent researchers in the past, are perfectly in line with the general theorem.

Appendix

1) Prove that when $\lambda <x_1$ and $\lambda =x_{m-1}-\left(m-1\right)$ is $\lambda =x_1-1=x_2-2=\cdots =x_{m-1}-\left(m-1\right)$.

Is, ( $\lambda <x_{m-2}$ and $\lambda =x_{m-1}-\left(m-1\right)$ or $x_{m-1}-\left(m-1\right)<x_{m-2}\iff x_{m-1}-x_{m-2}<m-1$ or $x_{m-1}-x_{m-2}=0$ or $x_{m-1}-x_{m-2}=1$ or $x_{m-1}-x_{m-2}=i$, where $i=2,3,\cdots ,m-2$. Condition $x_{m-1}-x_{m-2}=1$ is accepted, while the others are easily rejected. If $x_{m-1}-x_{m-2}=0\iff x_{m-1}=x_{m-2}$ (no true) and if $x_{m-1}-x_{m-2}=i\iff x_{m-1}=x_{m-2}+i$ or $\lambda =x_{m-1}-\left(m-1\right)=x_{m-2}+i-\left(m-1\right)=x_{m-2}-\left[m-\left(i+1\right)\right]$ (no true), because $x_{m-2}-\left[m-\left(i+1\right)\right]>x_{m-1}-\left(m-1\right)$. Indeed, if we consider that, $x_{m-2}-\left[m-\left(i+1\right)\right]>x_{m-1}-\left(m-1\right)\iff \left(m-1\right)-\left[m-\left(i+1\right)\right]>x_{m-1}-x_{m-2}\ge 1$ or $i>1$ or $i\ge 2$ (it is true, also the condition $x_{m-1}-x_{m-2}=i$ is not true). So, we have: $x_{m-1}=x_{m-2}+1$, therefore $\lambda =x_{m-1}-\left(m-1\right)\iff \lambda =\left(x_{m-2}+1\right)-\left(m-1\right)\iff \lambda =x_{m-2}-\left(m-2\right)$. We repeat the same procedure for the couple $x_{m-2},x_{m-3}$ and for all other similar pairs, thus proving the condition (2.12).

2) Prove that $\lambda \ne x_{m-1}-\left(m-1\right)$, when $x_{i-1}\le \lambda <x_i$ and $2\le i\le m-1$, by applying mathematical induction

If $\lambda =x_{m-1}-\left(m-1\right)$, combining Equation (2.6) Equation (2.18) we have:

${\left(x_1\right)}^n+\cdots +{\left(x_{i-1}\right)}^n+{\left(\lambda +i\right)}^n+\cdots +{\left(\lambda +m-1\right)}^n={\left(2\lambda +m-1\right)}^n$ (a.1)

By applying mathematical induction we have:

- For $m=3$, from Equation (a.1) we have:

${\left(x_1\right)}^n+{\left(\lambda +2\right)}^n={\left(2\lambda +2\right)}^n$ (a.2)

Also, is: ${\left(x_1\right)}^n+{\left(\lambda +2\right)}^n\le {\lambda }^n+{\left(\lambda +2\right)}^n<{\left(\lambda +\lambda +2\right)}^n={\left(2\lambda +2\right)}^n$.

So, for $m=3$, the condition (a.2) is not applies, therefore, is:

${\left(x_1\right)}^n+{\left(\lambda +2\right)}^n\ne {\left(2\lambda +2\right)}^n$.

- For $m=k$, we suppose that is true the following condition:

${\left(x_1\right)}^n+\cdots +{\left(x_{i-1}\right)}^n+{\left(\lambda +i\right)}^n+\cdots +{\left(\lambda +k-1\right)}^n\ne {\left(2\lambda +k-1\right)}^n$ (a.3)

- We will prove and for $m=k+1$ is true that:

${\left(x_1\right)}^n+\cdots +{\left(x_{i-1}\right)}^n+{\left(\lambda +i\right)}^n+\cdots +{\left(\lambda +k-1\right)}^n+{\left(\lambda +k\right)}^n\ne {\left(2\lambda +k\right)}^n$ (a.4)

Combining the conditions (a.3) and (a.4) we have,

${\left(x_1\right)}^n+\cdots +{\left(x_{i-1}\right)}^n+{\left(\lambda +i\right)}^n+\cdots +{\left(\lambda +k-1\right)}^n\ne {\left(2\lambda +k-1\right)}^n+{\left(\lambda +k\right)}^n$.

Suffice it to prove that: ${\left(2\lambda +k-1\right)}^n+{\left(\lambda +k\right)}^n\ne {\left(2\lambda +k\right)}^n\iff$

${\left(\lambda +k+\lambda -1\right)}^n+{\left(\lambda +k\right)}^n\ne {\left(\lambda +k+\lambda \right)}^n\iff {\left(1+\frac{\lambda –1}{\lambda +k}\right)}^n+1\ne {\left(1+\frac{\lambda }{\lambda +k}\right)}^n$ or

$1\ne {\left(1+\frac{\lambda }{\lambda +k}\right)}^n-{\left(1+\frac{\lambda –1}{\lambda +k}\right)}^n\iff 1\ne r^n-{\left(r-\frac{1}{\lambda +k}\right)}^n$, ( $r=1+\frac{\lambda }{\lambda +k}$ ) (a.5)

If, $1>r^n-{\left(r-\frac{1}{\lambda +k}\right)}^n\iff \frac{1}{r^n}>1-{\left(1-\frac{1}{r\left(\lambda +k\right)}\right)}^n>1-1=0$ (true, so the

Condition (a.5) also is true and consequently and the condition (a.4)). So, in this case be $\lambda \ne x_{m-1}-\left(m-1\right)$.

3) Justification for selecting the inequality $y\ge \frac{2n}{n-1}>\lambda n$ in B₁ of problem 2

The inequality $y\ge \frac{2n}{n-1}>\lambda n$ was written this way, with the following reasoning: Hypothesizing that is $\lambda n\ge \frac{2n}{n-1}$ we have: $\lambda n\ge \frac{2n}{n-1}\iff \lambda \ge \frac{2}{n-1}$. The maximum value of $\frac{2}{n-1}$ occurs when $n=2$ or ${\left(\frac{2n}{n-1}\right)}_{\max }=\frac{2}{2-1}=2$ and therefore is $\lambda \ge 2$. However, it is known from the Greek ancient times that if $1<n<3$ or $n=2$, the Equation (1.1) has solutions and for $\lambda =1$. But, this is an absurd and for this reason in this case condition $\lambda n\ge \frac{2n}{n-1}$ is rejected. Considering now, that $n\ne 2$ and hypothesizing for $n\ge 3$ that $\lambda n\ge \frac{2n}{n-1}$, then again we have: $\lambda n\ge \frac{2n}{n-1}\iff \lambda \ge \frac{2}{n-1}$. Its maximum value of $\frac{2}{n-1}$ occurs when $n=3$ or ${\left(\frac{2n}{n-1}\right)}_{\max }=\frac{2}{3-1}=1$ and therefore is $\lambda \ge 1$, since it is $\frac{2}{n-1}>0$ for

each $n\ge 3$. This, according to the logic by which the solution of the problem was constructed in this article, means that the Equation (1.1) has solutions for all $n\ge 3$ (because the value of λ greater or equal than number one or $\lambda \ge 1$ for all $n\ge 3$ ). However, this conclusion is in stark contrast to the conclusion in B₁, which resulted from a valid 100% inequality and is therefore an absurd. That is

why inequality $\lambda n\ge \frac{2n}{n-1}$ again is rejected and so we consider that inequality $\frac{2n}{n-1}>\lambda n$ is acceptable and therefore we ended up in inequality $y\ge \frac{2n}{n-1}>\lambda n$.

4) Justification for selecting the inequality $x_{m-1}\ge \frac{n\left(m-1\right)}{\left(n-m+2\right)}>\frac{n}{m-2}\lambda$ in B₂ of problem 2

The inequality $x_{m-1}\ge \frac{n\left(m-1\right)}{\left(n-m+2\right)}>\frac{n}{m-2}\lambda$ was written this way, with the following reasoning: For $m=3$, the previous inequality becomes $y\ge \frac{2n}{n-1}>\lambda n$. Thus, with the same explanation as in case B₂ of the problem 1 it turns out that the inequality $y\ge \frac{2n}{n-1}>\lambda n$ is rejected. Because, according to the logic by

which the solution of the problem was structured in this paper, the Equation (2.1) always has solutions for $\lambda \ge 1$, regardless of the parameters n and m, therefore the previous conclusion for $m=3$ is an absurd. That is why and the general

inequality $\frac{n}{m-2}\lambda \ge \frac{n\left(m-1\right)}{\left(n-m+2\right)}$ is rejected and therefore we consider that the inequality $\frac{n\left(m-1\right)}{\left(n-m+2\right)}>\frac{n}{m-2}\lambda$ is acceptable and so we ended up in inequality $x_{m-1}\ge \frac{n\left(m-1\right)}{\left(n-m+2\right)}>\frac{n}{m-2}\lambda$.

5) Prove that, when the Equation (2.1) has positive integer solutions, is $\lambda <x_{m-1}$.

We have: $\lambda <x_{m-1}-\left(m-1\right)<x_{m-1}$ $\iff$ $\lambda <x_{m-1}$.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Lebesgue, V.A. (1853) Solving Biquadratic Equations z2 = x4 ± my4, z2 = 2mx4 – y4, 2mz2 = x4 ± y4. Journal de Mathématiques Pures et Appliquées, 18, 73-86.
[2]	Hilbert, D. (1897) The Theory of Algebraic Number Fields. Annual Report of the German Association of Mathematicians, 4, 175-546.
[3]	Lenstra, Jr., H.W. (1992) On the Inverse Fermat Equation. Discrete Mathematics, 106-107, 329-331. https://doi.org/10.1016/0012-365X(92)90561-S
[4]	Richinick, J. (2008) The Upside-Down Pythagorean Theorem. Mathematical Gazette, 92, 313-317. https://doi.org/10.1017/S0025557200183275
[5]	Carmichael, R.D. (1913) On the Impossibility of Certain Diophantine Equations and Systems of Equations. American Mathematical Monthly (Mathematical Association of America), 20, 213-221. https://doi.org/10.1080/00029890.1913.11997962
[6]	Kronecker, L. (1901) Lectures on Number Theory, Vol. I. Teubner, Leipzig, 35-38.
[7]	Hancock, H. (1931) Foundations of the Theory of Algebraic Numbers, Vol. I. Macmillan, New York.
[8]	Ribenboim, P. (1979) 13 Lectures on Fermat's Last Theorem. Springer Verlag, New York, 202. https://doi.org/10.1080/00029890.1913.11997962
[9]	Singh, S. (1997) Fermat’s Last Theorem. Anchor Books, USA, 315.
[10]	Lehmer, D.H. (1968) Machines and Pure Mathematics. In: Computers Mathematical Research, North-Holland Publ. Co, Amsterdam.