Perturbation Analysis of Continuous-Time Linear Time-Invariant Systems

Peter Chang-Yi Weng^1*, Frederick Kin Hing Phoa²

¹Guangdong-Taiwan College of Industrial Science and Technology, Dongguan University of Technology, Dongguan, China.
²Institute of Statistical Science, Academia Sinica, Taiwan.

DOI: 10.4236/apm.2020.104010                

Abstract

In this paper, we consider the perturbation analysis of linear time-invariant systems, which arise from the linear optimal control in continuous-time. We provide a method to compute condition numbers of continuous-time linear time-invariant systems. It solves the perturbed linear time-invariant systems via Riccati differential equations and continuous-time algebraic Riccati equations in finite and infinite time horizons. We derive the explicit expressions of measuring the perturbation bounds of condition numbers with respect to the solution of the linear time-invariant systems. Furthermore, condition numbers and their upper bounds of Riccati differential equations and continuous-time algebraic Riccati equations are also discussed. Numerical simulations show the sharpness of the perturbation bounds computed via the proposed methods.

Keywords

Continuous-Time Linear Time-Invariant System, Condition Number, Perturbation Bound, Riccati Differential Equation, Continuous-Time Algebraic Riccati Equation

1. Introduction

Many mathematical models of physical, biological and social systems involve partial differential equations (PDEs). In order to understand these systems, we consider problems of control and optimization, leading to PDE boundary control, optimization constrained by stochastic PDEs, model order reduction and some related applications.

Consider the continuous-time linear time-invariant system (CLTI) by discretizing the PDE,

$\begin{array}{l}\stackrel{\dot{}}{x}\left(t\right)=Ax\left(t\right)+Bu\left(t\right),\mathrm{<mi>\; </mi>}x\left(0\right)=x_0,\mathrm{<mi>\; </mi>}t\in \left[0,t_1\right],\\ y\left(t\right)=Cx\left(t\right),\end{array}$ (1)

with coefficient matrices $A\in {ℝ}^{n\times n}$ , $B\in {ℝ}^{n\times m}$ , $C\in {ℝ}^{r\times n}$ , state vector $x\left(t\right)\in {ℝ}^n$ , control vector $u\left(t\right)\in {ℝ}^m$ and output vector $y\left(t\right)\in {ℝ}^r$ . We can apply the optimal control u to influence the state vector x for output vector y. From control theory, we seek to find the optimal control via solving the Riccati differential equation (RDE) in the finite time. For infinite time, we solve the continuous-time algebraic Riccati equation (CARE).

We solve the (perturbed) CLTI to get the relative errors in the exact solutions via RDEs and CAREs in the finite and infinite time horizons respectively. For solving RDEs, Leipnik [1] used the canonical form of the self-adjoint RDEs to obtain a convenient explicit solution. Rusnak [2] proposed an almost analytic representation for the solution of the nonhomogeneous and homogeneous, time invariant, and time variant RDEs to discuss the behavior of the optimal estimator on a finite time interval. For solving CAREs, it has been an extremely active area of research in various years. Laub [3] proposed the Schur method. Byers [4] suggested a stable symplectic orthogonal method as well as the matrix sign function method [5]. Guo and Lancaster [6] applied the Newton’s method. Benner and Byers [7] adopted a modified Newton’s method for solving CAREs that used exact line search to improve the convergence behavior of Newton’s method. Furthermore, Chu et al. [8] used the SDA.

Perturbation analysis considers the sensitivity of the solution to the small perturbations in the input data of a problem. A condition number, which is a measurement of the sensitivity, is important in the numerical computation. Furthermore, perturbation bounds are usually discussed. Kenney and Hewer studied the sensitivity of the RDEs developed by Byers [9] in [10]. Konstantinov and Pelova presented linear and nonlinear methods for estimating the sensitivity of the solution to RDEs in [11]. Konstantinov et al. [12] [13] proposed new methods to improve the sensitivity estimate of RDEs in 2-norm. For the sensitivity analysis of the linear differential system, we refer papers [14] [15] [16] and their references therein. For the perturbation analysis and perturbation bounds of CAREs, please see [9] [10] [17] [18] [19] [20] [21]. In this paper, it is the first to consider the perturbation analysis of CLTI via RDEs and CAREs.

The paper is organized as follows. We introduce the CLTI, solve the perturbed CLTI with only one perturbed coefficient matrix via RDEs, discuss the sensitivity of the RDEs, compute condition numbers and perturbation bounds of the CLTI via RDEs and apply backward differentiation formula (BDF) to solve differential Lyapunov matrix equation (DLE) in Section 2. Section 3 discusses the CLTI via CAREs, the sensitivity of the CAREs, condition numbers and perturbation bounds of the CLTI via CAREs. The illustrative numerical examples are presented in Section 4. Section 5 concludes the paper.

2. Solving Continuous-Time Linear Time-Invariant System Via Riccati Differential Equation

In order to guarantee the existence and uniqueness of the state and output vectors, respectively in the CLTI (1), we assume that the condition $\det \left(r{I}_n-A\right)\ne 0$ holds, for some r. The linear-quadratic regulator (LQR) problem for finite time horizon seeks the optimal control $u\left(t\right)$ to minimize the cost function:

$J\left(u\mathrm{,}{Q}_1\mathrm{,}{t}_1\right)\equiv {\displaystyle {\int }_0^{t_1}}\left[y^{{\rm T}}\left(t\right)y\left(t\right)+u^{{\rm T}}\left(t\right)Ru\left(t\right)\right]\text{d}t+x^{{\rm T}}\left(t_1\right)Q_{1}x\left(t_1\right)\mathrm{,}$

for some $R>0$ and $Q_1\ge 0$ . The optimal control is given by

$u\left(t\right)=-R^{-1}{B}^{{\rm T}}X\left(t\right)x\left(t\right)\mathrm{,\; <mi>\; </mi>}t\in \left[\mathrm{0,}{t}_1\right]\mathrm{,}$ (2)

with $X\left(t\right)$ being the solution to the RDE:

$\stackrel{\dot{}}{X}\left(t\right)=-A^{{\rm T}}X\left(t\right)-X\left(t\right)A-H+X\left(t\right)GX\left(t\right)\mathrm{,\; <mi>\; </mi>}X\left(t_1\right)=Q_1\mathrm{,}$ (3)

where $G\equiv B{R}^{-1}{B}^{{\rm T}}$ and $H\equiv C^{{\rm T}}C$ .

In this paper, the Bernoulli substitution technique is applied to solve RDEs (3), then we can take the optimal control $u\left(t\right)$ (2) into the CLTI (1) and solve the ordinary differential equation (ODE) to get the state vector $x\left(t\right)$ . Furthermore, the output vector $y\left(t\right)$ can be also obtained. Please refer to Weng and Phoa [22] about the details of solving the CLTI (1) via RDEs (3).

2.1. Sensitivity of the Riccati Differential Equation

As we solve the CLTI (1) by applying RDEs (3), then the sensitivity of RDEs (3) is studied. We first derive two kinds of condition numbers and perturbation bounds before we present the sensitivity of CLTI (1).

The RDEs (3) study nonlinear matrix differential equations arising in optimal control, optimal filtering, $H_{\infty }$ -control of linear-time varying systems, differential games, etc.; see, e.g. [23] [24] [25] [26]. Moreover, there is a variety of methods in the literature to compute the solution of RDEs (3); see, e.g. [27] [28] [29].

First, we transform from the RDEs (3) with terminal condition into initial value condition. Let $P\left(t\right)=X\left(t_1-t\right)$ , then for $0\le t\le t_1$

$\stackrel{\dot{}}{P}\left(t\right)=H+A^{{\rm T}}P\left(t\right)+P\left(t\right)A-P\left(t\right)GP\left(t\right)\mathrm{,\; <mi>\; </mi>}P\left(0\right)=Q_1\mathrm{.}$ (4)

Suppose we add some small perturbations only to coefficient matrix A in the RDEs (3) due to some applications like electric circuit simulation and multibody dynamics [30]. Other two coefficient matrices B and C in the CLTI (1) are treated similarly step by step. The solution to perturbed Riccati differential equation (pRDE) is $\tilde{P}\left(t\right)=P\left(t\right)+\Delta P\left(t\right)$ , then we get

$\stackrel{\dot{}}{\tilde{P}}\left(t\right)=H+{\tilde{A}}^{{\rm T}}\tilde{P}\left(t\right)+\tilde{P}\left(t\right)\tilde{A}-\tilde{P}\left(t\right)G\tilde{P}\left(t\right)\mathrm{,\; <mi>\; </mi>}\tilde{P}\left(0\right)=Q_1+\Delta Q_1\mathrm{,}$ (5)

where $\tilde{A}=A+\Delta A$ is the perturbed coefficient matrix.

Dropping the second and high-order terms in (5) yields

$\Delta \stackrel{\dot{}}{P}\left(t\right)=A_g\left(t\right)\Delta P\left(t\right)+\Delta P\left(t\right)A_g^{{\rm T}}\left(t\right)+\Delta A^{{\rm T}}P\left(t\right)+P\left(t\right)\Delta A\mathrm{,}$ (6)

$\Delta P\left(0\right)=\Delta Q_1\mathrm{,0}\le t\le t_1\mathrm{,}Ag\left(t\right)\equiv A^{{\rm T}}-P\left(t\right)G\mathrm{.}$ (7)

Let ${\Phi }_g$ satisfy

${\stackrel{\dot{}}{\Phi }}_g\left(t\right)=A_g\left(t\right){\Phi }_g\left(t\right)\mathrm{,\; <mi>\; </mi>}{\Phi }_g\left(0\right)=I\mathrm{,\; <mi>\; </mi>\; 0}\le t\le t_1\mathrm{.}$ (8)

Define

${\Omega }_g^{-1}\left(Z\right)={\displaystyle {\int }_0^t}{\Phi }_g\left(t\right){\Phi }_g^{-1}\left(s\right)Z\left(s\right){\Phi }_g^{-{\rm T}}\left(s\right){\Phi }_g^{{\rm T}}\left(t\right)\text{d}s$ (9)

for any continuous matrix function $Z=Z\left(s\right)$ , $s\in \left[\mathrm{0,}t\right]$ . By variation method, $\Delta P\left(t\right)$ in (6) can be solved

$\Delta P\left(t\right)={\Phi }_g\left(t\right)\Delta Q_1{\Phi }_g^{{\rm T}}\left(t\right)+{\Theta }_g\left(\Delta A\right)\mathrm{,}$ (10)

where

${\Theta }_g\left(Z\right)\equiv {\Omega }_g^{-1}\left(Z^{{\rm T}}P\left(t\right)+P\left(t\right)Z\right)\mathrm{.}$ (11)

Since we only perturb the coefficient matrix A, we modify the condition theory of Rice [31] into

$C_{ϵ}^A\left(t\right)=sup\left\{\frac{\Vert \Delta X\left(t\right)\Vert }{ϵ\Vert X\left(t\right)\Vert }\mathrm{<mo>\; |\; </mo>}\Vert \Delta A\Vert \le ϵ\Vert A\Vert \mathrm{,\; <mi>\; </mi>}\Vert \Delta Q_1\Vert \le ϵ\Vert Q_1\Vert \right\}\mathrm{.}$

Taking the limit as $ϵ$ goes to zero, the condition number is defined:

$K_{RDE}^A=\underset{ϵ\to 0}{lim}{C}_{ϵ}^A\left(t\right)\mathrm{.}$

That is,

$K_{RDE}^A=\underset{ϵ\to 0}{\lim }\sup \left\{\frac{\Vert \Delta P\left(t_1-t\right)\Vert }{ϵ\Vert P\left(t_1-t\right)\Vert }\mathrm{<mo>\; |\; </mo>}\Vert \Delta A\Vert \le ϵ\Vert A\Vert \mathrm{,\; <mi>\; </mi>}\Vert \Delta Q_1\Vert \le ϵ\Vert Q_1\Vert \right\}\mathrm{.}$ (12)

The following theorem describes the condition numbers of RDEs using 2- and $\infty$ -norm.

Theorem 2.1. Using the notations given above, we can derive the explicit expressions and perturbation bounds for two kinds of condition numbers of the RDEs according to only perturbed matrix A

$K_{\mathrm{2\; <mo>\; \_\; </mo>}RDE}^A=\frac{m_1}{\Vert P\left(t_1-t\right)\Vert }\mathrm{,}$ (13)

$K_{\infty \mathrm{<mo>\; \_\; </mo>}RDE}^A=\frac{m_2}{{\Vert P\left(t_1-t\right)\Vert }_{\infty }}\mathrm{,\; <mi>\; </mi>\; 0}\le t\le t_1\mathrm{,}$ (14)

where

$m_1={\Vert {\Phi }_g\left(t_1-t\right)\Vert }^2\Vert Q_1\Vert +\Vert {\Theta }_g\Vert \Vert A\Vert \mathrm{,}$

$m_2={\Vert {\Phi }_g\left(t_1-t\right)\Vert }_{\infty }^2{\Vert Q_1\Vert }_{\infty }+{\Vert {\Theta }_g\Vert }_{\infty }{\Vert A\Vert }_{\infty }\mathrm{.}$

Proof. According to the above definition about the condition number of RDEs (12), we take 2-norm in (10) and substitute t into $t_1-t$ , then obtain

$\Vert \Delta P\left(t_1-t\right)\Vert \le {\Vert {\Phi }_g\left(t_1-t\right)\Vert }^2\Vert \Delta Q_1\Vert +\Vert {\Theta }_g\Vert \Vert \Delta A\Vert \mathrm{.}$

For $ϵ$ sufficiently small, with $\Vert \Delta A\Vert /\Vert A\Vert$ , $\Vert \Delta Q_1\Vert /\Vert Q_1\Vert \le ϵ$ , we can get

$\Vert \Delta P\left(t_1-t\right)\Vert \le {\Vert {\Phi }_g\left(t_1-t\right)\Vert }^2ϵ\Vert Q_1\Vert +\Vert {\Theta }_g\Vert ϵ\Vert A\Vert \mathrm{.}$

Divide by $ϵ\Vert P\left(t_1-t\right)\Vert$ to get

$\frac{\Vert \Delta P\left(t_1-t\right)\Vert }{ϵ\Vert P\left(t_1-t\right)\Vert }\le \frac{{\Vert {\Phi }_g\left(t_1-t\right)\Vert }^2\Vert Q_1\Vert +\Vert {\Theta }_g\Vert \Vert A\Vert }{\Vert P\left(t_1-t\right)\Vert }\mathrm{.}$

From (12), let $ϵ\to 0$ give

$K_{\mathrm{2\; <mo>\; \_\; </mo>}RDE}^A\le \frac{m_1}{\Vert P\left(t_1-t\right)\Vert }\mathrm{,\; <mi>\; </mi>\; 0}\le t\le t_1\mathrm{.}$

Analogously, we take $\infty$ -norm in (10) and change t into $t_1-t$ , then obtain

$\frac{{\Vert \Delta P\left(t_1-t\right)\Vert }_{\infty }}{ϵ{\Vert P\left(t_1-t\right)\Vert }_{\infty }}\le \frac{{\Vert {\Phi }_g\left(t_1-t\right)\Vert }_{\infty }^2{\Vert Q_1\Vert }_{\infty }+{\Vert {\Theta }_g\Vert }_{\infty }{\Vert A\Vert }_{\infty }}{{\Vert P\left(t_1-t\right)\Vert }_{\infty }}\mathrm{.}$

Let $ϵ\to 0$ , we can get

$K_{\infty \mathrm{<mo>\; \_\; </mo>}RDE}^A\le \frac{m_2}{{\Vert P\left(t_1-t\right)\Vert }_{\infty }}\mathrm{,\; <mi>\; </mi>\; 0}\le t\le t_1\mathrm{.}$

In order to compute two kinds of condition numbers and perturbation bounds of the RDEs efficiently, we let be the solution to the differential Lyapunov matrix equation (DLE)

(15)

where 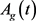is defined in (7) and 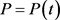is the solution of RDEs (4). We assume that 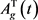is a c-stable matrix and therefore (15) has a unique symmetric solution [32]. The following theorem is the connection between DLE (15) and partial condition numbers (13) and (14).

Theorem 2.2. For, , 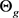and 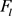as in (9), (11), and (15), respectively,

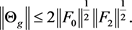
Proof. For, we let u and v be unit left and right singular vectors of 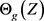such that

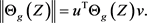
Using (9) and (11), we can obtain

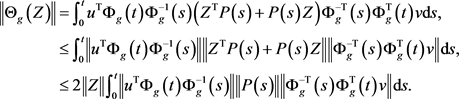
Applying the Cauchy-Schwarz inequality [21], we get

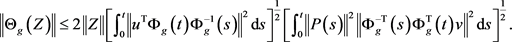
We can express the solution 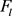to (15) explicitly using (8)

However,

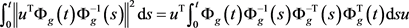(16)

(17)

where u is a unit vector. Moreover,

(18)

where v is a unit vector. Combining (17) and (18), we have

Thus,

2.2. Sensitivity of the CLTI via RDEs

In this subsection, we discuss the perturbation analysis of the CLTI (1) using RDEs (3) and derive two kinds of condition numbers. Furthermore, we also present their perturbation bounds.

Suppose we introduce some small perturbation only to coefficient matrix A and the state vector to the perturbed system is, then the perturbed CLTI is

(19)

We can replace the perturbed optimal control

and obtain

(20)

where is the perturbed coefficient matrix and is the solution of perturbed Riccati differential equation (pRDE):

(21)

Dropping the second and higher-order terms in (20) yields

(22)

where the pRDEs (21) are solved. Let satisfy

(23)

where

(24)

Define

(25)

for any continuous matrix function,. By variation method, we can solve (22) and get

(26)

The above relation discusses a first-order perturbation in the state vector corresponding to the perturbation. Based on the perturbation analysis for, we modify the condition theory of Rice [31] into

Taking the limit as goes to zero, we can get the condition number

The following theorem describes the condition numbers of the CLTI (1) via RDEs and perturbation bounds in 2- and -norm according to only perturbed matrix A.

Theorem 2.3. Using the notations given above, we can derive the explicit expressions and perturbation bounds for two kinds of condition numbers of the CLTI (1) via RDEs

where

Proof. We can investigate condition numbers in 2- and -norm according to only perturbed matrix defined by

(27)

For sufficiently small, with, , , we take 2-norm in (26) and get

Therefore, we can obtain

Thus gives

Analogously, we take -norm in (26) and apply (27), then obtain

Let, we can get

When we compute condition numbers and perturbation bounds of CLTI efficiently via solving RDEs, we let be the solution to the following DLEs

(28)

where is defined in (24). We assume that is a c-stable matrix and therefore (28) has a unique symmetric solution [32]. The following theorem states the solution of DLEs (28) that is equivalent to defined in (25).

Theorem 2.4. [23] For and as in (24) and (25), respectively, the unique solution of the DLEs (28) is defined by

where is defined in (23). Furthermore, we can obtain

Therefore,

2.3. Backward Differentiation Formula Method for Solving DLEs

There is a large variety of methods to compute the solution of DLEs, see, e.g. [27] [28] [29]. In this paper, we apply the efficient method called Backward Differentiation Formula (BDF) to (15), which can be treated (28) similarly.

Consider

(29)

Applying the fixed-coefficients BDF method to the DLEs (29), we obtain the matrix valued BDF scheme

where is the time step size, , , are the determining coefficients of the p-step BDF method as listed in Table 1 (see, e.g. [33]).

It leads to solving the following Lyapunov-BDF difference equation

with, , which can be written as the following Lyapunov equation

(30)

for and.

The Lyapunov Equation (30) can be solved by applying various methods such as the Schur vector method, symplectic SR methods, the matrix sign function, the matrix disk function or the doubling method; see, e.g. [34] [35] [36]. In this paper, we used the MATLAB function “lyap” to compute the unique symmetric positive semidefinite solution to the Lyapunov Equation (30).

Table 1. Coefficients of the p-step BDF method with.

3. Solving Continuous-Time Linear Time-Invariant System via Continuous-Time Algebraic Riccati Equation

For infinite time horizon, and we search for the steady state solution of the RDEs (3), which leads to the continuous-time algebraic Riccati equation (CARE):

(31)

In this case, the time-invariant solution X leads to the optimal control

(32)

In this paper, we used the MATLAB function “care” to compute the unique symmetric positive semidefinite solution X to the CAREs (31), then replace the optimal control (32) in the CLTI (1) and solve the ODE to get the state vector. Moreover, we can also obtain the output vector. For the details about the solvable conditions of CAREs (31) and solving the CLTI (1) via CAREs (31), please see Weng and Phoa [22].

3.1. Sensitivity of the Continuous-Time Algebraic Riccati Equation

Before we discuss the sensitivity of the CLTI (1) via solving CAREs (31), we first consider the sensitivity of the CAREs. Suppose we add some small perturbations only to the coefficient matrix A in the CAREs (31) similar to that in the RDEs (4), then we get the perturbed continuous-time algebraic Riccati equation (pCARE):

(33)

where. Dropping the second and high-order terms in (33) yields

(34)

Set

(35)

and let satisfy

Due to solvable conditions of CAREs (31), it is known that the matrix is c-stable [3] [9]. Furthermore, we can get that is invertible [37] and

(36)

Therefore, we can solve the Lyapunov Equation (34)

(37)

where

(38)

To connect to only, we modify the condition theory of Rice [31] into

Taking the limit as goes to zero, we obtain the condition number

(39)

The following theorem derives two kinds of condition numbers of CAREs (31) in 2- and -norm.

Theorem 3.1. Using the notations given above, we can derive the explicit expressions and perturbation bounds for two kinds of condition numbers of CAREs (31) according to only perturbed matrix A

(40)

(41)

where

Proof. For sufficiently small, with, we take 2-norm in (37) according to the definition of the condition number (39) and get

Divide by to get

Take and obtain

Analogously, we take -norm in (37) and divide, then we obtain

Let give

To solve two kinds of condition numbers and perturbation bounds of CAREs (31) efficiently, we let be the solution to the Lyapunov equation

(42)

where is defined in (35) and X is the solution of CAREs (31). The following theorem applies the Lyapunov equation (42) to compute the condition numbers (40) and (41) efficiently.

Theorem 3.2. For, and as in (36), (38) and (42), respectively

Proof. For, we let u and v be unit left and right singular vectors of such that

By (36) and (38), we get

Applying the Cauchy-Schwarz inequality, we obtain

We can express the solution of (42) explicitly [37]

(43)

But

(44)

where u is a unit vector. Moreover,

(45)

where v is a unit vector. Therefore, we combine (44) and (45), so

Thus,

3.2. Sensitivity of the CLTI via CAREs

We consider the perturbed CLTI (19) and take the perturbed optimal control

in (19), then obtain

(46)

By dropping the second and higher-order terms in (46), we apply the similar technique such as variation method to solve

and we obtain

(47)

with and being the following differentiation and integral functions, respectively

(48)

where is defined in (35).

The above relation (47) states a first-order perturbation in the state vector corresponding to only one perturbation matrix. From the perturbation analysis, we investigate two kinds of condition numbers according to only perturbed matrix A in the CLTI (1) via CAREs (31) in the following theorem.

Theorem 3.3. Using the above notations, the explicit expressions and perturbation bounds for two kinds of condition numbers in the CLTI (1) via CAREs (31) according to only perturbed matrix A are

(49)

(50)

where

Proof. We consider condition numbers of the CLTI (1) via CAREs (31) according to only perturbed matrix A in 2- and -norm defined by

(51)

For sufficiently small, with, , , we take 2-norm in (47) and get

According to the above definition of the condition number, we obtain

Let give

Analogously, we take -norm in (47) by applying (51) and obtain

Take, we can get

To solve two kinds of condition numbers of CLTI (1) via CAREs (31) efficiently, we apply Theorem 3.2 to compute condition numbers (49) and (50) efficiently.

Theorem 3.4. For and as in (35) and (48), respectively, the unique solution of the Lyapunov Equation (42) is represented in (43), then we can get

Thus,

4. Numerical Examples

The numerical simulations are conducted on a desktop with a 3.40 GHz Intel Core 2 Duo processor and 32 GB RAM, with machine accuracy. We compute with MATLAB [38] Version R2017b.

We have chosen one example for demonstration:

1) The example 1 illustrates condition numbers and perturbation bounds of CLTI via solving RDEs and CAREs with finite and infinite time horizons, respectively to present the effectiveness of the theoretical results.

Example 1 (CLTI)

Consider the CLTI (1) with and:

satisfying

with the optimal controls chosen through minimizing the cost functional

In the example, the perturbed coefficient matrix is constructed such as and, for, being the weighted coefficient. From the tables, ,

and are solutions of pRDEs, pCLTI and pCAREs, respectively, then we obtain relative differences of solutions between original and perturbed equations in 2- and -norm such as, , , , and and the corresponding perturbation bounds, , , , , , and according to only perturbed coefficient matrix.

Moreover, some parameters are set below:

for perturbation bounds of RDEs, CLTI and CAREs, respectively; the time range is for CLTI via solving RDEs and CAREs with a division 15 parts; the parameter of the weighted coefficient is fixed into; the terminal time is.

From Table 2, we skip the relative differences of RDEs in -norm as. We can observe sharper perturbation bounds of the relative differences in RDEs and CLTI such as,

Table 2. Example 1 (Condition numbers and perturbation bounds of CLTI solved by RDEs;, ,).

, and.

Table 3 shows that condition numbers of CLTI via solving CAREs are closely bounded by perturbation bounds such as

, , and.

To sum up, perturbation bounds of CLTI are tight around according to the weighted coefficient 10⁻³ whatever we solve via RDEs or CAREs.

5. Conclusion

We have proposed, tested and analyzed CLTI for the condition numbers and perturbation bounds according to only one perturbed coefficient matrix via solving RDEs and CAREs. Numerical simulations show that condition numbers provide tight perturbation bounds of the solutions to CLTI under some small

Table 3. Example 1 (Condition numbers and perturbation bounds of CLTI solved by CAREs;, ,).

change in the only one coefficient matrix. In summary, we introduce some efficient measurement tools for the sensitivity analysis of CLTI via solving RDEs and CAREs respectively.

Acknowledgements

This work was supported by Academia Sinica (Taiwan) grant number 103-CDA-M04, and Ministry of Science and Technology (Taiwan) grant numbers 104-2118-M-001-016-MY2 and 105-2118-M-001-007-MY2.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Leipnik, R.B. (1986) A Canonical Form and Solution for the Matrix Riccati Differential Equation. Bulletin of the Australian Mathematical Society, 26, 355-361. https://doi.org/10.1017/S0334270000004550
[2]	Rusnak, I. (1988) Almost Analytic Representation for the Solution of the Differential Matrix Riccati Equation. IEEE Transactions on Automatic Control, 33, 191-193. https://doi.org/10.1109/9.388
[3]	Laub, A.J. (1979) A Schur Method for Solving Algebraic Riccati Equations. IEEE Transactions on Automatic Control, AC-24, 913-921. https://doi.org/10.1109/TAC.1979.1102178
[4]	Byers, R. (1986) A Hamiltonian QR-Algorithm. SIAM Journal on Scientific and Statistical Computing, 7, 212-229. https://doi.org/10.1137/0907015
[5]	Byers, R. (1987) Solving the Algebraic Riccati Equation with the Matrix Sign Function. Linear Algebra and Its Applications, 85, 267-279. https://doi.org/10.1016/0024-3795(87)90222-9
[6]	Guo, C.-H. and Lancaster, P. (1998) Analysis and Modification of Newton’s Method for Algebraic Riccati Equations. Mathematics of Computation, 67, 1089-1105. https://doi.org/10.1090/S0025-5718-98-00947-8
[7]	Benner, P. and Byers, R. (1998) An Exact Line Search Method for Solving Generalized Continuous-Time Algebraic Riccati Equations. IEEE Transactions on Automatic Control, AC-43, 101-107. https://doi.org/10.1109/9.654908
[8]	Hu, E.K.-W, Fan, H.-Y. and Lin, W.-W. (2005) A Structure-Preserving Doubling Algorithm for Continuous-Time Algebraic Riccati Equations. Linear Algebra and Its Applications, 396, 55-80. https://doi.org/10.1016/j.laa.2004.10.010
[9]	Byers, R. (1985) Numerical Condition of the Algebraic Riccati Equation. In: Datta, B.N., Ed., Contemporary Mathematics: Vol. 47, Linear Algebra and Its Role in System Theory, AMS, Providence, 35-49. https://doi.org/10.1090/conm/047/828291
[10]	Kenney, C. and Hewer, G. (1990) The Sensitivity of the Algebraic and Differential Riccati Equation. SIAM Journal on Control and Optimization, 28, 50-69. https://doi.org/10.1137/0328003
[11]	Konstantinov, M. and Pelova, G. (1991) Sensitivity of the Solution to Differential Matrix Riccati Equations. IEEE Transactions on Automatic Control, 36, 213-215. https://doi.org/10.1109/9.67297
[12]	Konstantinov, M. and Angelova, V. (1997) Sensitivity Analysis of the Differential Matrix Riccati Equation Based on the Associated Linear Differential System. Advances in Computational Mathematics, 7, 295-301. https://doi.org/10.1023/A:1018903104476
[13]	Konstantinov, M., Popchev, I. and Angelova, V. (1994) A New Approach to the Sensitivity Analysis of Differential Matrix Riccati Equation. National Conference Automatica, Sofia, 94.
[14]	Golub, G. and van Loan, C. (1983) Matrix Computations. Johns Hopkins University Press, Baltimore.
[15]	Konstantinov, M., Petkov, P., Gu, D. and Postlethwaite, I. (1995) Perturbation Technique for Linear Control Problems. Report 95-7, Department of Engineering, Leicester University, Leicester.
[16]	Petkov, P., Christov, N. and Konstantinov, M. (1991) Computational Methods for Linear Control Systems. Prentice-Hall, Hemel Hempstead.
[17]	Chen, C.-H. (1988) Perturbation Analysis for Solutions of Algebraic Riccati Equations. Journal of Computational Mathematics, 6, 336-347.
[18]	Ghavimi, A.R. and Laub, A.J. (1995) Backward Error, Sensitivity, and Refinement of Computed Solutions of Algebraic Riccati Equations. Numerical Linear Algebra with Applications, 2, 29-49. https://doi.org/10.1002/nla.1680020104
[19]	Konstantinov, M., Petkov, P. and Christov, N. (1990) Perturbation Analysis of Matrix Quadratic Equations. SIAM Journal on Scientific and Statistical Computing, 11, 1159-1163. https://doi.org/10.1137/0911065
[20]	Sun, J.-G. (1998) Perturbation Theory for Algebraic Riccati Equations. SIAM Journal on Matrix Analysis and Applications, 19, 39-65. https://doi.org/10.1137/S0895479895291303
[21]	Xu, S.-F. (1996) Sensitivity Analysis of the Algebraic Riccati Equations. Numerische Mathematik, 75, 121-134. https://doi.org/10.1007/s002110050233
[22]	Weng, P.C.-Y. and Phoa, F.K.H. (2018) Calibrating Linear Continuous-Time Dynamical Systems via Perturbation Analysis. Filomat, 32, 1909-1915. https://doi.org/10.2298/FIL1805909W
[23]	Abou-Kandil, H., Freiling, G., Ionescu, V. and Jank, G. (2003) Matrix Riccati Equations in Control and Systems Theory. Birkhäuser, Basel. https://doi.org/10.1007/978-3-0348-8081-7
[24]	Ichikawa, A. and Katayama, H. (1999) Remarks on the Time-Varying H∞ Riccati Equations. Systems & Control Letters, 37, 335-345. https://doi.org/10.1016/S0167-6911(99)00041-9
[25]	Jacobs, O.L.R. (1993) Introduction to Control Theory. 2nd Edition, Oxford Science Publication, Oxford.
[26]	Petersen, I.R., Ugrinovskii, V.A. and Savkin, A.V. (2000) Robust Control Design Using H∞ Methods. Springer-Verlag, London. https://doi.org/10.1007/978-1-4471-0447-6
[27]	Choi, C. and Laub, A.J. (1990) Efficient Matrix-Valued Algorithms for Solving Stiff Riccati Differential Equations. IEEE Transactions on Automatic Control, 35, 770-776. https://doi.org/10.1109/9.57015
[28]	Dieci, L. (1992) Numerical Integration of the Differential Riccati Equation and Some Related Issues. SIAM Journal on Numerical Analysis, 29, 781-815. https://doi.org/10.1137/0729049
[29]	Kenney, C. and Leipnik, R.B. (1985) Numerical Integration of the Differential Matrix Riccati Equations. IEEE Transactions on Automatic Control, 30, 962-970. https://doi.org/10.1109/TAC.1985.1103822
[30]	Pulch, R. (2011) Polynomial Chaos for Linear Differential Algebraic Equations with Random Parameters. International Journal for Uncertainty Quantification, 1, 223-240. https://doi.org/10.1615/Int.J.UncertaintyQuantification.v1.i3.30
[31]	Rice, J. (1966) A Theory of Condition. SIAM Journal on Numerical Analysis, 3, 287-310. https://doi.org/10.1137/0703023
[32]	Mori, T., Fukuma, N. and Kuwahara, M. (1986) On the Lyapunov Matrix Differential Equation. IEEE Transactions on Automatic Control, 9, 868-869. https://doi.org/10.1109/TAC.1986.1104416
[33]	Ascher, U.M. and Petzold, L.R. (1998) Computer Methods for Ordinary Differential Equations and Differential Algebraic Equations. SIAM, Philadelphia. https://doi.org/10.1137/1.9781611971392
[34]	Datta, B. (2004) Numerical Methods for Linear Control Systems. Elsevier Academic Press, Boston.
[35]	Lancaster, P. and Rodman, L. (1995) Algebraic Riccati Equations. Clarendon Press, Oxford.
[36]	Mehrmann, V. (1991) The Autonomous Linear Quadratic Control Problem. Lecture Notes in Control and Information Sciences, Vol. 163, Springer-Verlag, Berlin. https://doi.org/10.1007/BFb0039443
[37]	Lancaster, P. (1970) Explicit Solutions of Linear Matrix Equations. SIAM Review, 12, 544-566. https://doi.org/10.1137/1012104
[38]	Mathworks (2010) MATLAB User’s Guide.