A Review of the Application of Nuclear Magnetic Resonance in Petroleum Industry ()
1. Introduction
Measurement of nuclear magnetic resonance relaxation is commonly used in the petroleum industry to investigate the relationship between the fluid in the pore scale and the formation in the subsurface or in the laboratory. NMR well logging application has been used in the study of conventional petroleum formations to detect water content and hydrocarbon and also to evaluate key reservoir properties such as porosity, permeability, and pore size distribution [1] [2].
Recently, the study of sediment at the near surface has been improved using new advances of NMR instruments and borehole instruments resulting in the increase in the use of NMR for the assessment of aquifers to estimate pore-size distribution, content of water, porosity, and hydraulic conductivity [3] [4].
Pore size distribution derived from NMR requires information about the surface relaxivity that implies that the main source of proton relaxation in reservoir rocks is due to the interaction of water with the surface of the grains. Often, in an exploration program, several physical properties of probable reservoirs are measured in the well site, including NMR relaxation times for saturating fluids and possibly their diffusion coefficients.
Under certain assumptions, diffusion coefficients and relaxation times correlate with the rock pores geometry and specifically pore sizes. Therefore, these techniques are widely used for rock porosity determination and permeability prediction.
Apart from NMR field instruments, petrophysical parameters can be improved by laboratory NMR instruments used to characterize the NMR response of materials, as well as to test innovative applications of NMR, such as determining the size and orientation of clay platelets and estimating immobile and mobile porosity [5] [6].
The NMR amplitude signal is an exponential decay which is converted into distribution of relaxation time, and the initial signal amplitude, A0 is directly proportional to the number of relaxing protons as well as the volume of water present within a sample. For NMR research, it is often assumed that the measured sample is fully saturated [e.g. [7] - [11] ], and in this case, A0 is equal to the total porosity. In like manners, in a saturated sample, the T2 distribution is related to the pore size distribution when relaxation occurs in the fast diffusion regime [11] [12] [13]. The geometric mean of the relaxation time obtained from the T2-distribution is equal to the average pore radius also related to the surface-area-to-volume ratio [11]. Surface relaxivity is a constant of proportionality that relates the T2-distribution to the surface-area-to-volume ratio, and the surface relaxivity is useful in the estimation of permeability (e.g. Knight et al., 2012). Surface relaxivity is also used for converting the T2 distribution to pore size distribution, and this can be influenced by the presence of paramagnetic and magnetic impurities on the surface of the grains causing the relaxation to be very fast [14]. Several studies have discovered that the presence of iron and manganese in a sample or formation increases the surface relaxivity [15] [16]. Likewise, minerals such as siderite and pyrrhotite containing iron have also been shown to increase the surface relaxivity [17]. The review of the advances in NMR well logging and laboratory measurements is aimed at explaining basic principles and interpretations needed to understand NMR formation evaluation to geologist, Petrophysicist, geophysicist, and engineers. A focus on unconventional reservoirs was explained because of the complexity of the rocks and fluids in the unconventional reservoirs, which can not be evaluated by traditional techniques. NMR as developed as one of the best tool for quantifying reservoir properties, fluid properties as well as determining reservoir productivity.
2. Theory of Nuclear Magnetic Resonance
Nuclear magnetic resonance (NMR) is simply the reaction of protons to magnetic fields. Several protons have a spin or angular momentum and net magnetic moment. Precession occurs to a proton in the presence of an external magnetic field around the same direction of the external field, similar to the way a gyroscope precesses around the earth’s gravitational field. Signals are produced and measured when these spinning magnetic nuclei interact with the external magnetic fields. There are some criteria that need to be met for measurement of NMR, which include a nucleus that has an odd number of neutrons or protons or both, examples of such nucleus are hydrogen (1H), carbon (13C), and sodium (23Na). For several of the nuclei found in subsurface, the borehole NMR logging tool cannot detect the NMR signal induced by external magnetic fields because it is too small. Whereas, hydrogen is abundant in both water and hydrocarbon and it also has only one proton and no neutrons, with a relatively great magnetic moment and hence produces a strong signal. Therefore, to date, almost all NMR logging and NMR rock studies are based on responses of the nucleus of the hydrogen atom. Because of this, occasionally the word “nuclear” is removed from “NMR (nuclear magnetic resonance)”, and instead “(MR) magnetic resonance” logging or “(MRI) magnetic resonance imaging” logging is used. This study will concentrate on proton NMR (i.e. hydrogen).
The hydrogen atom nucleus consists of a proton, which is a small, positively charged particle with a spin or angular momentum. The spinning proton signifies a current loop that produces a magnetic moment with two poles (north and south) aligned with the spin axis. Hence, the hydrogen proton can be thought of as a bar magnet with the magnetic axis that is aligned with the spin axis of the nucleus, as shown in Figure 1 (left). When several hydrogen atoms are present and there is no external magnetic field, then the nuclear spin axes are erratically aligned, as seen in Figure 1 (right).
2.1. Polarization
The first step in the measurement of Nuclear Magnetic Resonance (NMR) is to align the magnetic nuclei with a static magnetic field denoted as B0. When the static magnetic field (B0) is applied to a magnetic nucleus, B0 applies a force on the nucleus that acts to align B0 with the axis of the nuclear spin. Precession is the motion of an object that occurs when a torque is exerted on a spinning object,
the axis of the spinning object rotates perpendicular to the torque, as shown in Figure 2 (left). Therefore, when B0 is applied to a magnetic nucleus, the magnetic nucleus will precess around B0. The precessional frequency (f) is called the Larmor frequency, and it is given by
(1)
where γ is the gyromagnetic ratio, which represents the strength of the nuclear magnetism.
For hydrogen, γ/2π = 42.58 MHz/tesla. Other nuclei have other γ values [18]. Equation (1) represents the Larmor frequency for a given nucleus, which is proportional to the magnitude of the static magnetic field (B0) and the gyromagnetic ratio of the given nucleus.
When an external magnetic is applied to a proton, the proton is forced into one of two energy states. As indicated in Figure 2 (right), the energy state of a
![]()
Figure 1. A diagrammatic representative of hydrogen protons behaving as small magnet and without any external magnetic field the protons are randomly aligned [19].
![]()
Figure 2. In the presence of an external magnetic field, the proton spins at a Larmor frequency which depends on the proton’s gyromagnetic ratio [19].
particular proton rest on the direction of the precessional axis of the proton in relation to the direction of the external field. When the precessional axis is parallel to B0, then the proton is in the low-energy state, which is the ideal state. While when the precessional axis is anti-parallel to B0, the proton is in the high-energy state. The direction of B0 is called the longitudinal direction. When a great number of spinning protons are precessing about B0, as shown in Figure 2, more spins are precessing parallel to B0 than anti-parallel. The difference between the number of protons aligned parallel and anti-parallel to the B0 field forms the bulk magnetization M0 that provides the signal measured by NMR and MRI devices [18]. The macroscopic magnetization M0 is defined as the net magnetic moment per unit volume. For the case of N nuclei per unit volume, the magnetization is given by Curie’s Law as:
(2)
where
k = Boltzman’s constant;
T = absolute temperature (Kelvin);
h = Planck’s constant;
I = the spin quantum number of the nucleus.
2.2. Pulse Tipping and Free Induction Decay
The next step in the measurement of NMR is the tilting of the magnetization from the longitudinal direction to a transverse plane. This tilting is achieved by applying an oscillating magnetic field (B1) perpendicular to B0, the static magnetic field. For effective tilting, the frequency of B1 must be equal to the Larmor frequency of the protons relative to B0. From the quantum mechanics point of view, if a proton is at the low-energy state, it is possible to absorb energy provided by B1 and jump to the high-energy state. The application of B1 also causes the protons to precess in phase with one another. This change in energy state and in-phase precession caused by B1 is known as nuclear magnetic resonance.
On a macroscopic level, resonance results in the tipping of the magnetization, which precesses around B0 at the Larmor frequency [18] [20]. The angle through which the magnetization is tipped is given by
(3)
where
θ = tip angle (degrees);
B1 = amplitude of the oscillating field;
τ = time over which the oscillating field is applied;
The tip angle is thus proportional to the product B1τ, which imitates the energy that B1 supplies to the proton spin system. The tip angle is increased when the strength or the time of the oscillating field is increased. Equation (3) shows the relationship between the tip angle. In NMR logging the B1 field used is a pulsed oscillating magnetic field. Angular-pulse terms, such as a π pulse (or 180˚ pulse) and a π/2 pulse (or 90˚ pulse) are the angle through which B1 tips the magnetization. When an NMR tool applies a 90˚ B1 pulse to the proton population that the tool has polarized, the protons precess in phase in transverse planes (relative to B0). Macroscopically, magnetization is tipped 90˚ and precesses in the transverse plane [19].
When the B1 field is turned off, the proton population begins to dephase or lose phase coherence—that is, the precessions of the protons will no longer be in phase with one another. Therefore, as dephasing progresses, the net magnetization decreases. In this situation, a receiver coil that measures magnetization in the transverse direction will detect a decaying signal as shown in Figure 3.
Dephasing can be reversed by applying a 180˚ pulse of the oscillating magnetic field B1 and this enables the proton to precess in phase again and ultimately producing a measurable signal which is called the Spin-Echo as shown in Figure 4.
![]()
Figure 3. Dephasing of protons after B1 removal and the decay signal it generates [21].
![]()
Figure 4. Rephasing process through applying the 180˚ pulse and the generation of a Spin Echo [21].
Applying the 180˚ pulse repeatedly helps to produce a series of spin-echo that are formed in between consecutive pulses. After several rephasing process through the application of several 180˚ pulses (Figure 5), however, the protons cannot be refocused because of molecular interaction which results in the decaying of the spin-echo series. The NMR tool measures the decaying signal of the spin echoes.
3. NMR Petrophysical Measurements
NMR Laboratory studies are generally carried out in the oil and gas industry to evaluate rock cores as well as estimate petrophysical relationships between parameters of interest to the oil industry (such as porosity permeability, irreducible water, and oil saturation) and NMR parameters [11] [13]. Until lately, it was believed that the petrophysical relations established in the oil industry might well be directly used for the interpretation of measurements in the near-surface. For example, earlier studies thought that the NMR T2 measurement made the in earth’s magnetic field should be equal to NMR T2 measurement made in lab-NMR systems [10] [22]. Current studies in the laboratory have revealed that these values are the same only under specific conditions [23]. For instance, the presence of paramagnetic, magnetic minerals, and clay content, which are often found in near-surface sediments, can increase T2 relaxation [23] [24].
Extensive laboratory studies on NMR responses and on the properties of fluid-saturated porous media have been carried out from the start of NMR as well as the advance of nuclear magnetic resonance-logging tools. The outcomes of these studies have established the petrophysical foundation on which logging measurements and interpretation models and applications can be built on.
![]()
Figure 5. For a spin-echo train to be created, a CPMG pulse sequence is used, which consists of a 90˚ B1 pulse followed by a series of 180˚ B1 pulses. Spin echoes of reducing amplitude follow the 180˚ B1 pulses [19].
Innovative pulse-NMR spectrometers were invented simultaneously with logging tools to duplicate the core samples analysis in the laboratory with the borehole measurements [25] [26]. The NMR instruments work and record data in the same way as NMR-logging tools [27]. Low-field Nuclear Magnetic Resonance spectrometers offer the ability to produce repeatable measurements of fluid and rock NMR properties. This ability helps the calibration and correlation of field measurements and laboratory, and it can also be used to relate the interpretation models established in the laboratory to logging data. In cases where core samples are unavailable for NMR-log calibration, recent advances and techniques now make NMR petrophysical measurements on drill cuttings possible [28]. Nuclear Magnetic Resonance Laboratory studies are usually carried out for the following purposes:
· Validating formation porosity.
· Building models to forecast changes in pore size (facies).
· Building models to recognize and calculate hydrocarbons, as well as residual oil.
· Building specific models for formation-specific which increases the precision of estimating free-fluid index (FFI), bulk-volume-irreducible (BVI) water, and eventually, permeability.
· Assessing the effect of texture on NMR responses, such as microporosity.
3.1. Porosity
NMR T2 relaxation (decay) measurement is used to estimate porosity from NMR logs. Therefore, the hydrogen molecules in the fluid-filled pore spaces of the formation are equivalent to NMR porosity (whether the fluid is water, oil, or gas).
The original amplitude of the spin-echo train is equal to the number of the hydrogen nuclei present in the fluid-filled pore spaces within the sensitive volume. The amplitude is calibrated in porosity unit, and the precision of the amplitude measurement relies on some factors such as:
1) A satisfactorily long polarization time denoted as TW. The TW is required to reach total polarization of the hydrogen nuclei in the fluids, but when TW is too short, it results in the underestimation of porosity estimated from NMR.
2) It is also important to have short inter-echo spacing denoted as TE, which is essential to record the fast-relaxing fluid decay related to highly viscous oils. When the TE is too long, the estimation of microporosity.
3) The quantity of hydrogen nuclei in the fluid should be equivalent to the amount in an equal volume of water (i.e., HI = 1); a porosity correction is needed when the HI (Hydrogen Index) of any of the fluids in the pore spaces is less than 1.
Porosity is one of the essential reservoir properties that are needed in the petroleum industry and also one of the earliest NMR measurements. All things being equal, interpretation of the porosity measurement depends on many factors such as whether hydrocarbon is present or not, the age of the logging tool, and the type of fluid in the pore space.
NMR estimated porosity is different from conventional neutron and density porosity logs because NMR porosity is independent of mineralogy except when the formation contains a significant amount of ferromagnetic and/or paramagnetic minerals. In this case, it is possible to underestimate porosity from NMR logs because some of the T2 relaxations are too fast to measure. So overall, in most cases, NMR porosity is considered a lithology-independent measurement (Figure 6).
[29] presented a method of estimating porosity in low porosity rocks by using a Magic Sandwich Echo (MSE) pulse sequence. They compared their result with the traditional NMR porosity calculation and noticed more accuracy with their MSE method. They also suggested a method of estimating the total organic carbon (TOC) content of shales which is a useful parameter for the evaluation of shale reservoirs.
[30] presented NMR porosity of irregular shaped drill cuttings. They addressed the challenges associated with estimating porosity from drill cuttings by including a higher frequency multinuclear NMR method. The methodology is successfully demonstrated on both core and irregularly shaped simulated cuttings from conventional and unconventional shale plays.
3.2. Permeability
NMR log and measurements are essential in the ability to estimate the real-time permeability, which is calculated from empirical relationships between porosity derived from NMR and T2LM. There are two empirical relationships: the Schlumberger-Doll Research (SDR) equation and the Timur-Coates equation. This relationship was discovered in the laboratory during several core samples experiment. The Schlumberger-Doll Research is an empirical equation given as:
![]()
Figure 6. An example of density porosity logs in carbonates comparing it to lithology-independent porosity derived from NMR [31].
(4)
where:
is the effective porosity from NMR.
T2LM is the geometric mean of the T2 relaxation time.
C is a lithology-dependent variable. In sandstone, C is equal to 4, while in carbonate, C is equal to 0.1. The Timur-Coates model is also known as the free fluid model, and it is given by the equation below
(5)
is the effective porosity from NMR.
FFI is the free fluid index which is the fractional part of formation volume occupied by movable fluids.
BVI is the Bulk Volume Irreducible which is the fractional part of formation volume occupied by immobile, capillary bound water.
Both SDR and Timur-Coates permeability equations are based on some assumptions that are not applicable in carbonates because the NMR measured pore size distribution and pore throat sizes cannot be well correlated in carbonates. Likewise, carbonates can have addition NMR signal from fluids in isolated in vugs, which overestimate porosity calculation but not permeability. One of the challenging areas of NMR research is in the estimation of permeability in carbonates reservoirs.
The Schlumberger-Doll Research model works well in water-saturated reservoirs or samples. When oil or oil filtrates are present, the T2 is close to the T2 bulk as a result of the effect of partial polarization, which causing an overestimation of permeability in oil zones. T2LM is relatively low in unflushed gas zones compared to flushed zones, and this results in an underestimation of permeability. The effect of hydrocarbon on T2LM makes SDR models to be unreliable in hydrocarbon-bearing formation because the T2LM is uncorrectable. Coates model can be applied in formations containing water and/or hydrocarbons. The average-T2 model can be applied to pore systems containing only water [32]. The Timur-Coates and Schlumberger-Doll model are only applicable to estimate matrix permeability while it is inapplicable in formations that are fractured.
[19] obtained two echo train from two formations with different permeability but the same porosity with different pores sizes. This difference causes T2 distribution to shift resulting in different values of the ratio of MFFI (Movable Free Fluid Index) to (Bulk Volume Irreducible) BVI (Figure 7). Estimated permeability using the Coates model is indicated in Figure 8.
To calibrate the Timur-Coates model to core, Equation (5) is solved as a straight line, y = mx + b:
(6)
![]()
Figure 7. A plot of two echo trains produced from rocks of different pore sizes but similar porosity showing disparity in T2 data with permeability [19].
![]()
Figure 8. Determining the Coates permeability model constant C using a cross plot that utilizes core data [19].
Assuming b is equal to 0 in equation 6, k is substituted for core permeability while m the slope of the line is estimated using a least-squares regression.
[33] worked on calculating permeability using NMR based on pore sizes in a limestone reservoir. They transformed four different pore sizes into NMR T2 spectrum using the shape as well as the turning point of mercury intrusion capillary pressure curves. This was used to develop a new permeability calculation model based on pore sizes, and this model was used in different blocks, and the result was more reliable than the traditional methods of calculating permeability.
[34] worked on estimating permeability from shales from NMR time-dependent methane saturation. The permeability of shales is challenging because of the presence of clay and its tightness. They defined a single exponential decay formula to calculate permeability, and this was validated by reservoir simulation to confirm its reliability. They also develop a multiexponential model to differentiate between low and high permeability in shales. The understanding of permeability of shales is crucial for the development of shale reservoirs and oil production.
3.3. Wettability
Wettability is the ability of a fluid to stick to the surface of a solid in the presence of another immiscible fluid [35]. The spreading of a fluid on the surface of the solid is generally described as wetting. Wettability can be measured by adhesion tension, a function of the interfacial tension which controls which fluid will likely wet the solid.
When two immiscible fluids like oil and water are in contact with a solid, the contact angle which is used to measure the adhesion tension is measured from the liquid phase that is denser and it ranges from 0 to 180 (Figure 9). The adhesion tension can be measured using Equation (7) below:
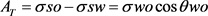 (7)
(7)
σos = interfacial energy between oil and solid (dyne/cm).
σws = interfacial energy between water and solid (dyne/cm).
σow = interfacial energy, or IFT, between oil and water (dyne/cm).
θ = contact angle at oil-water-solid interface measured through the water phase (degrees).
The wettability of reservoir rocks is crucial because it affects the oil’s effective permeability and the efficiency of oil recovery.
The wettability of the reservoir rocks controls the distribution of water and oil, and this also controls the flow of fluid through pore spaces. It is challenging to understand wettability in porous media, and several researches have been done to understand it better [36] [37] [38] [39]. No method exists that can estimate wettability in situ, and hence it is essential to measure the wettability of reservoir rocks from laboratory measurements.
![]()
Figure 9. Contact angles of different fluid such as oil, water, and mercury.
There are also several studies on the wettability problem using NMR, however, there is no commonly agreed method for quantifying wettability, and these studies are mostly done in the laboratory on core samples [40] - [45].
[40] studied wettability using an NMR method that involves the mixtures of oil wet sands and water wet sands to determine the fluid distribution in the pore system. Nuclear Magnetic Resonance measurements are sensitive to wettability measurements since the pore surface is promoting the relaxation rate of the wetting fluid. [40] discovered a linear relationship between fractionally preferentially oil-wet surface and preferentially water-wet sand and nuclear magnetic resonance rate of water as shown in Figure 10. [46] also discovered a relationship between endpoints and relative T2 of an oil peak for measurements performed at Rørdal chalk and this study was also extended to Edwards limestone.
The linear relationship discovered by [40] explains that the oil-wet surface has a lower surface relaxivity than the water wet surface, and the linear disparity of the relaxation rate reflects the abundance of the oil-wet surfaces.
One of the NMR methods used in measuring wettability is the T2 based wettability, it is a recent method technique [47] [48] [49] [50] which compared to early research is more than a single pore size or fluid saturation and hence T2 component is considered.
 (8)
(8)
![]()
Figure 10. Relaxation rates for sand mixtures containing various percentages of oil wet sand [40].
T2 can be determined from numerous parameters and one of the parameters is wettability, pore size distribution, surface relaxivity, and fluid viscosity. This means that to calculate wettability from T2 measurement, it is essential to have several additional information. All this information can be gotten from downhole measurement and the laboratory.
Another NMR technique used for measuring wettability is T2 versus saturation; this technique is a simple derivative of the T2 based wettability discussed above. In this method, the effective fluid volumes V changes with saturation meanwhile the effective surface S doesn’t change. The effective surface S is equal to zero in a non-wetting fluid. This means that the second part of equation 8 is equal to zero, meaning that measured T2 of the fluid to be equal to T2 bulk value and independent of saturation.
[51] [52] [53] are examples of researchers that used this technique in estimating wettability. This method is usually qualitative, and it is useful in the downhole measurement where the tool has multiple depths of investigation (DOI). A recent work by [54] focused on a method that is applicable in the downhole based on restricted diffusion. They described an improved technique of separating the oil and water signal in the 2D maps in addition to the diffusion map compared to T2 based approach. Effective surface relaxivities of oil and water and Archie’s cementation exponent “m” can be calculated from the 2D map using restricted diffusion for a specific fluid within the pore size distribution. Because the effective surface relaxivities are dependent on the saturation of the fluid and T2 surface relaxation, the rock relaxivity, and wettability index can be estimated.
3.4. NMR Oil Viscosity
Viscosity is the measure of the easy of fluid flow, the thicker the oil, the higher the viscosity and the slower it flows. NMR measurement is also used to determine oil viscosity by using the equation below.
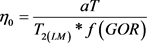 (9)
(9)
where
η0 is the oil viscosity.
T is oil temperature in Kelvin.
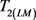 is the T2 geometric mean.
is the T2 geometric mean.
f (GOR) is a dimensionless function of the Gas-Oil ratio.
a is equal to 0.004 (s∙cp∙K−1).
Another equation for calculating oil viscosity that uses the molecular diffusion coefficient D is shown below:
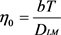 (10)
(10)
where
b is equal to 5.05 × 10-8 (cm2∙s−1∙cp∙K−1).
DLM is the geometric mean of the D value and a unit of cm2/s.
T is the temperature in Kelvin.
One essential parameter calculated from the inversion of the NMR decay data is the T2 logarithm mean known as the T2LM of the fluid. This denotes the mean T2 location of the fluids.
For estimating the viscosity of oil, it is vital to know the bulk relaxation of the fluid, which is the relaxation that happens when atomic nuclei transfer energy through local diffusion, and this represents the property of the fluid. The bulk relaxation is the relaxation time of the fluid in a container measured in a homogenous field. The bulk relaxation rate is affected by the molecular oil weight, the molecular oil size, and the molecular rigidity.
[55] describes three different methods of predicting the viscosity of heavy oil by integrating TE-dependent T1 and T2 NMR relaxation, Hydrogen Index (HI), and temperature. The three methods show the practical application of NMR measurement in predicting the viscosity of oil. Compared to other previous researches, [55] presented an improved correlation that enables prediction over a wide range of viscosity values. Their result also shows that the effect of heavy-oil samples should be considered when used for viscosity prediction and core analysis protocols.
[56] presented a method of determining in-situ viscosity of fluids in a porous media using physical simulation and NMR. The result shows that the viscosity distribution of water is not constant and heterogenous, which can be linked to the distance between the walls of the rock and water. They also demonstrated that under the same centrifugal pressure, as the water separated from the rock increases, the average in-situ viscosity of the water also increases, and this can be associated with an increase in permeability.
4. NMR Properties of Fluid
In the 1950s, researchers originally assumed that the hydrogen nuclei in brine and oil-saturated formation would relax at the same rate as the bulk fluid. The brine and oil in the rocks can be identified from the difference between the relaxation rate. The researchers also assumed that formation porosity would be estimated using the tool since the initial amplitude signal of the NMR decay was equal to the quantity of hydrogen in the formation. Therefore, to effectively interpret relaxation measurements in rocks saturated with fluids, then it is vital to separate the contributions of surface relaxation from bulk relaxation as well as diffusion induced relaxation (Table 1).
In NMR research, water, oil, and gas are the fluid of interest in a reservoir, the water salinity varies from salt-saturated (mostly NaCl) to nearly pure. The gas can be free gas, mainly methane, while the oil can be dead oil (free of gas) or live oil (gas saturated). Live oil occurs at high temperatures and high pressures when the dissolved gas in the oil is below the bubble point.
4.1. NMR of Bulk Water
The relaxation time of bulk water at room temperature and at low magnetic field varies from 1 to 3 seconds in a T1 and T2 NMR well logging as shown in Figure 11. There is variation in the T1 and T2 in the bulk water because of the presence of dissolved oxygen, which is paramagnetic [57]. Paramagnetic ion and minerals have been shown to reduce the value of T1 and T2 in water.
The NMR relaxation of brine depends on the type of salt that is dissolved in the water, as the presence of a small concentration of paramagnetic ions can reduce the water response significantly.
The possibility of water to fill the small pores and the long relaxation of bulk water are the key reasons why the surface relaxation controls the brine relaxation in porous media.
4.2. NMR of Bulk Crude Oil
Oil often resides in the center of the pore space since it is a non-wetting fluid that doesn’t make contact with the grain surface [57]. The T2 relaxation time of bulk crude oil is a range of values rather than a single value and this is controlled by viscosity [58] [27]. As viscosity increases, the hydrogen nuclei become less mobile and thus quickly relax. Hence the T2 geometric mean gets shortened by an increase in viscosity. While the wide NMR distribution of bulk crude oil represents different oil components, the longer T2s in a crude oil T2 distribution
![]()
Table 1. NMR properties of reservoir fluids [19].
![]()
Figure 12. NMR distribution of bulk crude oil.
correspond to signals from mobile molecules. In contrast, the short T2s are associated with signals from larger molecules (Figure 12).
More viscous oils are often composed of a wider variety of hydrocarbons. Even some light oils have multiple components and can exhibit a broadened T2 distribution. NMR T2 measurements on several crude oils with different viscosities.
[59] worked on how to distinguish heavy oil from bound water in T2 distribution despite the poor sensitivity of diffusion. It is difficult to calculate the total heavy oil as well as the producible volume, especially in shaly sandstone reservoir. They successfully used both conventional logs and NMR T2, to investigate heavy oil reservoirs in Buzachi field in Kazakhstan. They concluded that the integrated method helps to overcome the limitations of the single methods.
4.3. NMR Bulk of Gas
Spin relaxes in liquid and solids by dipole-dipole interaction, and the interaction of the magnetic of dipoles of interest with nuclei of the other dipole produces this relaxation [57].
For most liquids and solids, the spins relax by dipole-dipole interaction. This relaxation is caused by the interaction of the magnetic dipoles of the nucleus of interest with the dipoles of other nuclei. Methane is an example of a pure gas whose spin relaxes by spin-rotation interaction and this is the connection between the magnetic field generated by the spin of the molecule and the magnetic moments of the protons. The T1 relaxation of methane increases with increasing pressure and decreases with increasing temperature, which is the opposite behavior in liquids [57].
In a case when oil, gas, and water exist in the same pore space in a rock, both gas and light oil can be easily identified using their T1 contrast. When oil-based mud is used in drilling, the signal of the crude oil, gas and oil-based mud filtrate will occur in the differential spectrum. Distinguishing between oil, gas, and oil-based mud filtrate is based on resolvable T2 differences in the differential spectrum [57].
5. NMR in Unconventionals Reservoirs
Unconventional reservoirs are hydrocarbon-bearing rocks that need advanced techniques to be able to produce hydrocarbon economically. Such reservoirs include heavy oil sandstones, gas shales, gas hydrates, tight gas sandstones, tight oil shale, and oil shale formation.
Unconventional reservoirs have been a great source of hydrocarbon production in the world and will continue to be a great source because with the increasing consumption of oil there is a need to find more ways to produce oil.
The relationship between rocks and fluids in the unconventional reservoirs is complex, and it is a vital problem in the oil industry because the traditional approaches of evaluating the formation are not reliable in unconventional reservoirs. NMR has become one of the significant methods of evaluating an unconventional reservoir, for estimating petrophysical parameters like porosity, permeability, and irreducible saturation. The ratio of T1/T2 using 2D NMR has been discovered to be useful for detecting oil, gas, water, bitumen, and fluid composition of kerogen in unconventional reservoirs.
Shale is an example of an unconventional reservoir that is rich in clays minerals and organic matter. The most abundant sedimentary rock is shale, and the presence of organic matter makes it a rich hydrocarbon source rock. Shale contains varieties of pore sizes with different kinds of fluids, which have fractional wettability; also, nano-scale pores in shale and its absorption properties make it more complex to study.
It is assumed that surface relaxation is the primary relaxation mechanism in the pore system of many conventional reservoirs. Hence the NMR T2 peak is directly proportional to the size of the pore that contains the fluid, and this helps to estimate pore size distribution in many reservoirs. In the case of shale, the primary relaxation is also surface relaxation, but believing that the relaxation interaction scale is proportional to the pore-scale investigated will make every study of pore size on NMR relaxation time meaningless [60]. The presence of many pore sizes in shale makes the interpretation complex because it will be difficult to conclude if different fluids in the pore cause the peaks in NMR distribution or different pore sizes.
In the case of Shale, NMR measurement is not independent of the rock matrix because they contain clay and organic matter, which are considered as matrix constituent and hydrogen nuclei that affect the NMR signal [61]. The organic content of shale affects the NMR signal in two ways. First, it affects the signal directly by adding to the population of the proton measured, and secondly, it controls the relaxation time of the fluid present in the organic pores where it acts as the surface relaxation. The effect of organic matter on NMR response in both cases above depends on its maturity. For the first case, the degree of maturation is directly proportional to the mobility of the hydrogen nuclei [60]. Hence the organic content signal from oil, gas and immature windows will be different.
The distribution and presence of clay make fluid identification complex in most unconventional reservoirs like shale, and likewise, this clay minerals add to the population of the proton which influences the signals of the fluid in the pore spaces in many various ways. Firstly, the NMR signal of clay minerals depends on their compaction and distribution in shales [62]. The NMR response of clay will be below 0.1 ms sometimes undetectable without high-resolution machine when the clay mineral is laminar or structural in distribution [60]. Whereas when the clay is dispersed, it will not generate a separate response, but instead, it will influence the fluids signals by providing additional surface area for fluid relaxation.
Secondly, the type of clay mineral in the rock will also influence the wettability of the pores. [63] compared the hydrophobicity of Kaolinite and Illites and found that Kaolinite is asphaltene-wet while Illite is water-wet. Therefore, according to clay type, clay will absorb different fluids.
In unconventional gas exploration, the pore size distribution of shale is essential [64] [65]. The laboratory study of NMR is not the same with well logs because of the scale; hence it is vital to understand T2 distribution in NMR logs to be able to understand how to appraise the pore size distribution of shale to evaluate the storage of gas [66].
[67] used NMR well logs in the Ordos basin to evaluate different pore size distribution. They separated various pore size distribution to 8 different relaxation time ranges using the NMR log, and this range of porosity was plotted against total NMR porosity. They discovered that the bound fluid volume has a relaxation time of < 4.5 ms, and this occupied the more significant part of the total NMR porosity. They also explained that the microfractures, bulk fluid volume, and routine free fluid volume are present in the shale gas reservoir. They also characterize porosity into three parts; bound fluid volume, which is the dominant, routine free fluid, and microfractures, which is the less dominant. They concluded that NMR well logs can estimate the pore type in shale accurately and that the three types of porosity can be estimated from NMR, which is essential for the exploration of shale gas.
[68] presented a novel technique for estimating the content of clay in tight oil reservoirs. They conducted NMR measurements on sandstone, which contains clay minerals of several types. Their result showed that the T2 cutoff value of clay-bound water is different for each clay type. This means that different values of T2 cutoff will be estimated using NMR logging while determining the clay bound water in a specific region. Using the clay water saturation and the cation exchange capacity, they observed the relation between clay content, clay water saturation, density logs, and neutron logs. They used the least-squares methods to estimate the content of clay-based on the relationships. In conclusion, they compared the calculated experimental result to the result obtained from the fields, and they agreed well proofing that the proposed method is reliable.
[69] studied the imbibition characteristics in the shale, which provides an understanding of low flowback efficiency and potentially affects the production of gas. The authors conducted a series of imbibition measurements on sandstone, continental shale, and marine shale samples. The NMR method was used to monitor the water distribution and migration in the samples. The imbibition rate has a positive relationship with the clay mineral content in both shale types, and unlike unswelling sandstone, with constant T2 values, the shales have varying T2 values during imbibition. The continental shale has a larger imbibition rate than marine shale because of high clay content. The marine shale T2 values increase incrementally because of the extension of microfractures, while for continental shales the T2 values reduce gradually, indicating the compaction of the matrix pore and this causes negative effects on gas flow channels. This study concludes that increasing shutting-in time in continental shale is not suitable while it is more suitable to shut-in in marine shale.
[70] conducted Low Field-NMR tests of T1 and T2 relaxation time on raw oil shale from the Eocene Green River Formation and pyrolyzed samples of these shales processed by hydrous pyrolysis and techniques to imitate surface and in-situ retorting. A plot of the typical T1 - T2 correlation plots described some distinct peaks demonstrative of liquid-like and solid organic phases, while the obtained results on the pyrolyzed shales show changes that take place during thermal processing. More signal was produced in the organic using the spin-echo measurement, showing that homonuclear-dipole coupling has a great influence on low field NMR relaxometry measurements of nuclei in solid and viscous organic matter of rock samples. This work concluded that low field NMR relaxometry could offer a lot of information on shales and other reservoir rocks that go well beyond porosity and pore-fluid analysis.
6. Conclusion
This paper reviewed the application of Nuclear Magnetic Resonance for formation evaluation in the petroleum Industry. The NMR theory and petrophysical measurement and its applications are discussed. This paper described the importance of using NMR logging and measurement to evaluate and calibrate petrophysical properties of reservoir rocks. The NMR logging or laboratory measurement is based on the response of nuclei atoms to a magnetic field. NMR logging demonstrates a better estimation of petrophysical properties such as porosity and permeability more than many conventional logging tools can achieve. These NMR applications enable geologists, geophysicists, and petrophysicists to have a better understanding of the reservoir properties that ensure proper reservoir management and optimization. Recent advances in the use of NMR in unconventional reservoirs were presented and to the best of the authors’ knowledge, this paper reviewed the most recent advances in NMR. Hence this paper gives an overview of the laboratory and borehole application of the NMR, which is capable of improving the successful evaluation of reservoir properties in both conventional and unconventional reservoirs.