Dependence Model Selection for Semi-Competing Risks Data

Jin-Jian Hsieh, Cheng-Fang Tsai

Department of Mathematics, National Chung Cheng University, Chiayi.

DOI: 10.4236/ojs.2020.102016                

Abstract

We consider the model selection problem of the dependency between the terminal event and the non-terminal event under semi-competing risks data. When the relationship between the two events is unspecified, the inference on the non-terminal event is not identifiable. We cannot make inference on the non-terminal event without extra assumptions. Thus, an association model for semi-competing risks data is necessary, and it is important to select an appropriate dependence model for a data set. We construct the likelihood function for semi-competing risks data to select an appropriate dependence model. From simulation studies, it shows the performance of the proposed approach is well. Finally, we apply our method to a bone marrow transplant data set.

Keywords

Copula Model, Likelihood Function, Model Selection, Semi-Competing Risks Data

1. Introduction

Semi-competing risks data [1] were often encountered in a biomedical study in which a terminal event censors a non-terminal event. A common example of the terminal event is death, and the non-terminal event usually is disease progression or relapse. When the relationship between the two events is unspecified, the inference on the non-terminal event is not identifiable. We cannot make inference on the non-terminal event without extra assumptions. Thus, an association model for semi-competing risks data is necessary for copula-based approaches [1] - [6], and it is important to select an appropriate dependence model for a data set. Hsieh et al. [4] used a distance measure between a non-parametric estimator and a model based estimator to select a proper dependence model. In this paper, we construct the likelihood function under several candidate models for the semi-competing risks data and use the likelihood function to select a most fitted model. In simulations, we compare our proposed methods with Hsieh et al. [4]. This paper is organized as follows. In Section 2, we introduce the structure of semi-competing risks data and copula models. In Section 3, we derive the likelihood function for semi-competing risks data and introduce three model selection methods. We examine the finite sample performance of the proposed methods and compare them with Hsieh et al. [4] in Section 4. In Section 5, we use the Bone Marrow Transplant data from Klein and Moeschberger [7] to illustrate our suggested methods. Finally, we make some conclusions in Section 6.

2. Data and Model Assumption

Semi-competing risks data consist of a terminal event and a non-terminal event, which a terminal event may censor a non-terminal event. Let T be the time from the initial event (e.g. disease diagnosis) to the non-terminal event (e.g. a status of disease progression), D be the time from the initial event to the terminal event (e.g. death), and C be the time from the initial event until lost to follow-up or the end of study. In general, we assume that C is independent of $\left(T\mathrm{,}D\right)$ . Define $X=\min \left(T,D,C\right)$ , $Y=\min \left(D,C\right)$ , ${\delta }_1=I\left(T\le Y\right)$ , and ${\delta }_2=I\left(D\le C\right)$ . The observed data can be denoted as $\left\{\left(X_i,Y_i,{\delta }_{1i},{\delta }_{2i}\right)|i=1,2,\cdots ,n\right\}$ .

With semi-competing risks data, we are interested in its dependence structure between T and D and require to ensure the validity for the inference of the non-terminal event time T. The most commonly used model for dependence is the copula model [8]. We assume $\left(T\mathrm{,}D\right)$ follow a copula model as

$Pr\left(T>t,D>d\right)=C_{\alpha }\left(S\left(t\right)\mathrm{,}{G}_1\left(d\right)\right)\mathrm{,}0\le t\mathrm{,}d\le \infty \mathrm{,}$ (1)

where $S\left(t\right)$ is the marginal survival function of T, $G_1\left(d\right)$ is the marginal survival function of D, $C_{\alpha }\left(\cdot \mathrm{,}\cdot \right)$ is a parametric copula function defined on a unit square, and indexed by a single real parameter, $\alpha$ , which is related to Kendall’s tau [9]. To define Kendall’s tau, suppose that $\left(T_1\mathrm{,}{D}_1\right)$ and $\left(T_2\mathrm{,}{D}_2\right)$ are two independent realizations of the joint distribution. Then, $\tau$ is the difference between the probability of concordance and the probability of discordance of these two observations, namely,

$\tau =Pr\left\{\left(T_1-T_2\right)\left(D_1-D_2\right)\ge 0\right\}-Pr\left\{\left(T_1-T_2\right)\left(D_1-D_2\right)<0\right\}\mathrm{.}$

A copula $C_{\alpha }$ is said to be (strictly) Archimedean copula (AC) when

$C_{\alpha }\left(u\mathrm{,}v\right)={\phi }_{\alpha }^{-1}\left({\phi }_{\alpha }\left(u\right)+{\phi }_{\alpha }\left(v\right)\right)\mathrm{,}$ (2)

for all $0\le u\mathrm{,}v\le 1$ , where the ${\phi }_{\alpha }\mathrm{<mo>\; :\; </mo>}\left(\mathrm{0,1}\right]\to R^{+}$ is a decreasing convex function satisfying ${\phi }_{\alpha }\left(1\right)=0$ and ${\phi }_{\alpha }\left(0^{+}\right)=\infty$ . We take the following three examples for Archimedean copula, the Clayton, Frank and Gumbel. The Clayton copula is given by

$C_{\alpha }\left(u\mathrm{,}v\right)={\left(u^{-\alpha }+v^{-\alpha }-1\right)}^{-1/\alpha }\mathrm{,}$

and its generator is

${\phi }_{\alpha }\left(t\right)=\left(t^{-\alpha }-1\right)/\alpha \mathrm{,}$

where $\alpha \in \left(\mathrm{0,}\infty \right)\backslash \left\{0\right\}$ . The relationship between Kendall’s tau $\tau$ and the Clayton copula parameter $\alpha$ is given by $\tau =\alpha /\left(\alpha +2\right)$ . The Frank copula is given by

$C_{\alpha }\left(u,v\right)=-\frac{1}{\alpha }\ln \left(1+\frac{\left(\exp \left(-\alpha u\right)-1\right)\left(\exp \left(-\alpha v\right)-1\right)}{\exp \left(-\alpha \right)-1}\right),$

and its generator is

${\phi }_{\alpha }\left(t\right)=-\ln \left(\frac{\exp \left(-\alpha t\right)-1}{\exp \left(-\alpha \right)-1}\right),$

where $\alpha \in \left(-\infty \mathrm{,}\infty \right)\backslash \left\{0\right\}$ . The relationship between Kendall’s tau $\tau$ and the Frank copula parameter $\alpha$ is given by $1+4\left\{D_1\left(\alpha \right)-1\right\}/\alpha$ , where $D_1\left(\alpha \right)={\displaystyle {\int }_0^{\alpha }}\left\{t/\alpha \left({\text{e}}^t-1\right)\right\}\text{d}t$ . The Gumbel copula is given by

$C_{\alpha }\left(u,v\right)=\exp \left\{-{\left[{\left(-\ln \left(u\right)\right)}^{\alpha +1}+{\left(-\ln \left(v\right)\right)}^{\alpha +1}\right]}^{1/\alpha +1}\right\},$

and its generator is

${\phi }_{\alpha }\left(t\right)={\left[-\ln \left(t\right)\right]}^{\alpha +1},$

where $\alpha \in \left(\mathrm{0,}\infty \right)$ . The relationship between Kendall’s tau $\tau$ and the Gumbel copula parameter $\alpha$ is given by $\tau =\alpha /\left(\alpha +1\right)$ .

3. The Proposed Model Selection Methods

In statistical analysis, model selection is an important issue. Several candidate models are considered to fit data. Which model is the most appropriate for the considered data? Under semi-competing risks data, the observed data can be denoted as $\left\{X_i,Y_i,{\delta }_{1i},{\delta }_{2i}|i=1,2,\cdots ,n\right\}$ . To specify the dependency of $\left(T\mathrm{,}D\right)$ , we usually assume $\left(T\mathrm{,}D\right)$ follows an AC model. Our goal is to choose a best copula model for the dependency of T and D among some candidate models, and the idea is to use the likelihood function information to choose the most fitted copula model from a candidate copula model set. Therefore, we need to derive the likelihood function under different copula models. We derive the likelihood function by considering the four possible situations for the values of ${\delta }_1$ and ${\delta }_2$ . Let $S\left(t\right)$ be the survival function of T, $f_T\left(t\right)$ be the pdf of T, $G_1\left(d\right)$ be the survival function of D, $g_1\left(d\right)$ be the pdf of D, $G_2\left(y\right)$ be the survival function of C, and $g_2\left(y\right)$ be the pdf of C. For each case, we write a Randon-Nikodým derivative

of the distribution of $\left(X\mathrm{,}Y\right)$ , and denote the $\frac{{\partial }^{i+j}}{\partial u^i\partial v^j}C\left(u\mathrm{,}v\right)$ by $C^{\left(i\mathrm{,}j\right)}\left(u\mathrm{,}v\right)$ .

· (Type A) If ${\delta }_1={\delta }_2=0$ , which means $X=Y=C$ ,

$P\left(X=x,Y=y,{\delta }_1=0,{\delta }_2=0\right)=g_2\left(y\right)C_{\alpha }^{\left(0,0\right)}\left(S\left(y\right),G_1\left(y\right)\right).$

· (Type B) If ${\delta }_1=0,{\delta }_2=1$ , which means $X=Y=D$ ,

· (Type C) If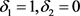, which means and,

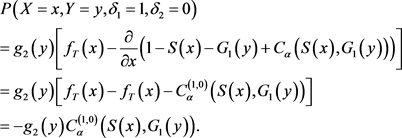
· (Type D) If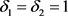, which means and,

Summarizing the above situations, we can derive the likelihood function for one observation as

(3)

We can use the Kaplan-Meier estimator to estimate based on data and define as. Then we have a likelihood function for the n observations as

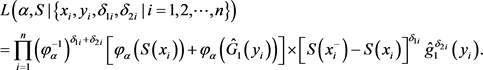(4)

Based on the likelihood function, we consider three approaches to select an appropriate copula model, which are

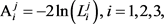(5)

where is the corresponding maximum likelihood function described in (4) based on the ith approach with, which is the jth candidate copula model. Suppose that there are M candidate copula models for consideration. For the ith method, we compute. Then, select a copula model with the smallest.

For the first method, , we use the estimator of by Lakhal et al. [3], which is extended from Zheng and Klein [10], and we have the likelihood as

(6)

Now this function can be represented in the form of only one unknown parameter. Next, we apply the in R to obtain the maximum likelihood, and define.

For the second method, , Kaplan-Meier [11] noted that the survival function can be written as, where

, and define as the sort of . So, there is a sequence corresponded to. By Lakhal et al. [3], we can estimate the parameter, which is also studied by Wang [2] and Heuchenne et al. [6]. From the above, we can write as

(7)

Next, we use the PSO (Particle Swarm Optimization, Kennedy and Eberhart [12]) algorithm, which is a computational approach that optimizes the corresponding likelihood function by iteratively trying to improve a candidate solution, to obtain the mle of h, which is denoted as, and define.

The third method, , is similar to the second method but the number of the maximizers in likelihood function are more than. We maximize the corresponding likelihood with respective to and simultaneously, and the corresponding likelihood function is

(8)

Then, use the PSO (Particle Swarm Optimization) algorithm to obtain the maximum likelihood, and define. The difference for the three methods is the maximizer number in the corresponding likelihood function. In simulations, we would compare the correct selection probability for the three methods.

4. Simulation Studies

This section examines the performance of the proposed model selection methods and compares it with Hsieh et al. [4] through several simulation settings. Simulated data are generated from three copula models which are the Clayton model, Frank model, and Gumbel model. Based on simulated data from one copula among the three copulas in the above, three candidate models are considered to fit the simulated data. There are two different settings under two different censoring rates:

High censoring rate:

Case 1:, , and.

(The censoring rate is about 42% for T and about 16% for D.)

Case 2:, , and.

(The censoring rate is about 33% for T and about 28% for D.)

Low censoring rate:

Case 3:, , and.

(The censoring rate is about 23% for T and about 12% for D.)

Case 4:, , and.

(The censoring rate is about 22% for T and about 14% for D.)

In the above situations, we also set three different Kendall’s tau, , and 0.8 to determine which model is the most fitted candidate for simulated data. The sample size is 100 with 500 replications.

Tables 1-4 summarize the simulation results, and it presents the model selected percentage under different simulation data. Note that is the method based on the approach, , and is the method by Hsieh et al. [4]. From the results, the performance of the three proposed selection methods is better than Hsieh et al. [4], especially for Frank and Gumbel models. Thus, our proposed methods are more stable than Hsieh et al. [4]. From the Tables, we can find that the probability of choosing a correct model rises with increasing Kendall’s tau, and also find that the performance under low censoring rate is better than high censoring rate. Based on the comparisons, we recommend using the first method, A₁, because it takes less computer running time than A₂ and A₃.

5. Data Analysis

In this section, we apply our proposed methods to analyze the bone marrow transplant data from Klein and Moeschberger [7]. There were 137 leukemia patients receiving bone marrow transplants. The data can be divided into three different groups, acute lymphoblastic leukemia (ALL) with 38 patients, acute myelocytic leukemia (AML) low-risk with 54 patients, and AML high-risk with 45 patients. Let T be the time to relapse of leukemia, D be the time to death, and C be the censoring time. The observed variables are, , , and. For each group, we choose the most fitted

Table 1. Model selection probabilities under.

C: Clayton; F: Frank; G: Gumbel.

Table 2. Model selection probabilities under.

C: Clayton; F: Frank; G: Gumbel.

Table 3. Model selection probabilities under.

C: Clayton; F: Frank; G: Gumbel.

Table 4. Model selection probabilities under.

C: Clayton; F: Frank; G: Gumbel.

model among the three models, Clayton, Frank, and Gumbel copula, by the four methods, and present the results in Tables 5-8. From the results, our methods choose Clayton copula for ALL group, AML high risk group, and all patients; select Gumbel model for AML low risk group. Hsieh et al. [4] choose Gumbel copula for ALL group, AML high risk group, and all patients; selects Frank copula for AML low risk group.

Table 5. The selected model for each method under ALL group.

Table 6. The selected model for each method under AML low risk group.

Table 7. The selected model for each method under AML high risk group.

Table 8. The selected model for each method under all patients.

6. Concluding Remarks

In this paper, we study the model selection problem under semi-competing risks data. Because the non-terminal event is dependently censored by the terminal event, we cannot make inference on the non-terminal event without extra assumptions. Thus, an association model for semi-competing risks data is necessary, and a model selection method is necessary for the association model. We construct the likelihood function for semi-competing risks data under a copula model and propose three approaches based on the likelihood function to select a fitted model. The simulation analysis shows the performance of the proposed methods are more stable than Hsieh et al. [4], and A₁ takes less time than A₂ and A₃. With covariates, we can stratify the data according to the covariates and apply the model selection approach for each stratum. For the continuous covariates, we can group it as a categorical variable. Finally, we apply our proposed methods to analyze the Bone Marrow Transplant data. Base on the selected model, an interesting problem is to consider the goodness-of-fit test, which is treated as future work.

Acknowledgements

This paper was financially supported by the Ministry of Science and Technology of Taiwan (MOST 108-2118-M-194-001-MY2).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Fine, J.P., Jiang, H. and Chappell, R. (2001) On Semi-Competing Risks Data. Biometrika, 88, 907-919. https://doi.org/10.1093/biomet/88.4.907
[2]	Wang, W. (2003) Estimating the Association Parameter for Copula Models under Dependent Censoring. Journal of the Royal Statistical Society: Series B, 65, 257-273. https://doi.org/10.1111/1467-9868.00385
[3]	Lakhal, L., Rivest, L.P. and Abdous, B. (2008) Estimating Survival and Association in a Semi-Competing Risk Model. Biometrics, 64, 180-188. https://doi.org/10.1111/j.1541-0420.2007.00872.x
[4]	Hsieh, J.J., Wang, W. and Ding, A.A. (2008) Regression Analysis Based on Semi-Competing Risks Data. Journal of the Royal Statistical Society: Series B, 70, 3-20.
[5]	Xu, J., Kalbfleisch, J.D. and Tai, B. (2010) Statistical Analysis of Illness-Death Processes and Semicompeting Risks Data. Biometrics, 66, 716-725. https://doi.org/10.1111/j.1541-0420.2009.01340.x
[6]	Heuchenne, C., Laurent, S., Legrand, C. and Keilegom, I.V. (2014) Likelihood Based Inference for Semi-Competing Risks. Communications in Statistics—Simulations and Computations, 43, 1112-1132. https://doi.org/10.1080/03610918.2012.725495
[7]	Klein, J.P. and Moeschberger, M.L. (2003) Survival Analysis Techniques for Censored and Truncated Data. Springer, New York. https://doi.org/10.1007/b97377
[8]	Genest, C. and MacKay, J. (1986) The Joy of Copulas: Bivariate Distributions with Uniform Marginals. The American Statistician, 40, 280-283. https://doi.org/10.1080/00031305.1986.10475414
[9]	Oakes, D. (1989) Bivariate Survival Models Induced by Frailties. Journal of the American Statistical Association, 74, 487-493. https://doi.org/10.1080/01621459.1989.10478795
[10]	Zheng, M. and Klein, J. (1995) Estimates of Marginal Survival for Dependent Competing Risks Based on an Assumed Copula. Biometrika, 82, 127-138. https://doi.org/10.1093/biomet/82.1.127
[11]	Kaplan, E.L. and Meier, P. (1958) Nonparametric Estimation from Incomplete Observations. Journal of the American Statistical Association, 53, 457-481. https://doi.org/10.1080/01621459.1958.10501452
[12]	Kennedy, J. and Eberhart, R. (1995) Particle Swarm Optimization. Proceedings of IEEE International Conference on Neural Networks, Vol. 4, 1942-1948. https://doi.org/10.1109/ICNN.1995.488968