1. Introduction
To understand the light, human being experienced three stages.
In the first stage, the knowledge of the human being regarding the light is mainly recorded as legend in each nation’s historical book or literature. Here we select two such kinds of legend from Chinese ancient literature as examples put in the appendix for the people who are interested to read [1] [2].
In the second stage, the human being enters the time of knowledge explosion. During this period, a series of famous scientists appear, such as Newton [3], Einstein [4], Huygens [5] and Maxwell [6]. Till now most of knowledge regarding the light is based on their achievements. For example, in order to explain the straight propagation of light, Newton proposes the light is composed of particles. Later on, Huygens and Young’s double slit experiments demonstrate the wave property of light. The Maxwell establishes equation and reveals the fact that the light is just the electromagnetic wave. And then, Einstein successfully explains the photon-electric effect with the particle property of light. In following day, each group of scientists try to prove the other side are wrong but failed, that is, the light always in some condition shows the particle character, in other condition, shows the wave property. Finally, both sides reach agreement on the fact that the light does have the particle and wave properties together, called “duality property”. Therefore, they invent a new word, “photon”, to describe this duality behavior of light.
Now the time (we can define as the third stage) enters the new era. The situation will be changed. In our previous work [7], we demonstrate that the light is not continuous but discontinuous instead. It is this discontinuous property of light that makes the light behave sometimes as a particle, sometimes as a wave. From our previous work, we also determine the basic unit of light as a photon and make clear the fact that a photon is just one wavelength in the space dimension and one period in the time dimension.
From these results, we can for the first time analyze the optical spectrum on the solid basis, such as analyzing the optical line width in the spectrum obtained from the spectrometer, because our previous work provides a clear starting point to distinguish the factors making the line in spectrum broadening. For example, the theoretical line width in the spectrum should be one period in time domain or one wavelength in space domain, all other factors, such as natural line broadening, thermal broadening, will cause the line in spectrum broadening further [8].
Based on the progress achieved in our previous works, here we will move one more step further, that is, what a photon really looks like?
2. Theoretical Consideration
Theoretically, we can take the simplest system, hydrogen atom, to start our discussion.
(1)
where H(1s) and H(2s) are the hydrogen atom at ground 1s state and excited 2s state, respectively.
This equation tells us that the hydrogen atom at the ground state, H(1s), can absorb a photon and be excited to the excited state, H(2s), and vice versa. During this process, the energy conservation should be valid, therefore, we can get,
(2)
where E(1s) and E(1s) (E2s and E1s) are the energies for hydrogen atom at 1s and 2s states, respectively; h is Plank constant, ν is frequency.
Based on the quantum mechanics [9] and electromagnetism [10], we know,
(3)
where N is the unit conversion factor to change the joule into the atomic unit;
and
are the wave functions for hydrogen atom at 1s and 2s states, respectively; H is the Hamilton operator for hydrogen atom; E and B are the electric and magnetic fields, respectively; ε and µ are the permittivity and permeability of vacuum, respectively.
From the principle of mathematical integration [11], we get,
(4)
Based on the electromagnetic theory [10], we know there is a relation between the electric field and the magnetic field as
where c is the speed of light in the vacuum.
Therefore, the last term in bracket can be combined as one term as
(5)
(6)
, where
(7)
(8)
(9)
(10)
where,
(11)
(12)
Therefore,
(13)
If we take the real parts of E and B, they are
(14)
If we take the imaginary parts of E and B, they are
(15)
Similarly,
(16)
where
is the wave function for hydrogen at excited state 2p0.
(17)
where
(18)
(19)
Therefore,
(20)
If we take the real parts of E and B, they are
(21)
If we take the imaginary parts of E and B, they are
(22)
In principle, we can get the expressions of E and B for the photon from all kinds of sources.
3. Discussion
From the result above, we notice that the photon is composed of the electric field and magnetic field which have the spacetime distributions. From the expressions of F2s-1s(r) and F2p0-1s(r, θ), it is obvious that the electric and magnetic fields distributions of photon are source dependent, that is, the photon from different origin has its own pattern of spacetime distribution. For example, comparing the photon from
and that from
, their E and B spacetime distributions are definitively different, but the energies of photon from both processes are the same.
At moment, we still don’t know whether these different E and B spacetime distributions of photon have effect on the optic process or not, and how these different spacetime distributions of E and B affect the optic process, especially the optical-chemical reaction, therefore, much more work should be done in this field.
For most of people, they know the E and B spacetime distributions of photon can be obtained by directly solving the Maxwell’s equation and the E and B spacetime distributions are always shown as the picture in Figure 1. Compared to our result above (see the expressions of F2s-1s(r) and F2p0-1s(r, θ)), they are totally different, and another obvious difference is in that for the spacetime distributions of the electric and magnetic fields from directly solving the Maxwell’s equation, it doesn’t matter the energies of photons are the same or not, they always share the similar spacetime distributions. It is very strange, to our knowledge, till now, nobody doubts this result, they all accept as it is. How to explain this conflict between our result and that from directly solving the Maxwell’s equation? Our understanding is, the result from the Maxwell’s equation corresponds to the photon which has no source, that is, the photon without the origin, but this situation doesn’t exist in reality. Each photon in reality does have
![]()
Figure 1. The Illustration of the spacetime distributions of electric and magnetic fields of electromagnetic wave by directly solving the Maxwell’s equation.
the source to create it, just like a bullet flying in spacetime, if the gun doesn’t exist to fire it, where this bullet comes from? We are surprised by that so simple fact is not paid attention to so long time by the scientific world. Fortunately, this situation is finally ended by our work here.
Before we discuss the potential applications of our result above, it should be pointed out the fact that from the whole history of science and technology, the developments of science and technology always promote each other. Sometimes the science promotes the development of new technology; sometimes the technology promotes the development of new branch of science. We hope someday in the future, we can not only distinguish the photon by its frequency and wavelength, but also by its spacetime distributions of electric and magnetic fields. As a result, the science will be promoted to the higher level of resolution and precision.
As a summary, based on our result in this work, we predict there are four major potential applications.
1) Information about the Light Source
From the result in this work, we know that the spacetime distributions of the electric and magnetic fields of photon are dependent on source, therefore, we can reversely get some information regarding the structure of the source from the spacetime distributions of the electric and magnetic fields of photon. For example, the photon from
has the spherical symmetry of the electric and magnetic fields spacetime distributions, that means the photon is created by the source which has spherical symmetry; whereas the photon from
doesn’t have the spherical symmetry of the electric and magnetic fields spacetime distributions, therefore, we know that the photon from 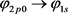 is created by the source which doesn’t have spherical symmetry.
is created by the source which doesn’t have spherical symmetry.
2) Optic-Chemical Reaction [12]
If we can determine which spacetime distributions of the electric and magnetic fields of photon will be more efficient to ignite the optic-chemical reaction, then we can utilize this property of photon to improve the energy efficiency in optic-chemical reaction. For example, the photon from the 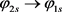 and the photon from the
and the photon from the 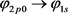 have the same frequency but their spacetime distributions of the electric and magnetic fields are different; therefore, their effect on the optic-chemical reaction should be different. If we can distinguish the photons from
have the same frequency but their spacetime distributions of the electric and magnetic fields are different; therefore, their effect on the optic-chemical reaction should be different. If we can distinguish the photons from 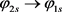 and from
and from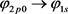 , then, the more detail mechanism of the optic-chemical reaction will be revealed.
, then, the more detail mechanism of the optic-chemical reaction will be revealed.
3) Optical Communication
To our knowledge, now the optical communication [13] is always realized by the modulation of the frequency or amplitude of the photon. Our work here offers the third way to make optical communication, that is, to decode the information carried by the photon by the spacetime distributions of the electric and magnetic fields of photon. In this way, the capacity of the information carried by the photon will be not limited by the range of frequency, such as band width, because even if the frequency of the photon is the same but the spacetime distributions of the electric and magnetic fields of photon are different.
4) Optical Computer
From the literature, one of the hot topics is the optical computing [14]. Our work offers a new way to develop the optical computer. For example, we can define the photon from 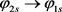 as 0, and the photon from
as 0, and the photon from  as 1. In this way, we can simplify the optical-computer and make calculation much faster and easier. Furthermore, our work also provides extra safety control for the data protection, that is, the data handled in the computing process are spacetime shape dependent.
as 1. In this way, we can simplify the optical-computer and make calculation much faster and easier. Furthermore, our work also provides extra safety control for the data protection, that is, the data handled in the computing process are spacetime shape dependent.
As we discussed above, all the applications mentioned here rely on the new technology development. We wish the new technology comes as earlier as possible.
4. Conclusion
In this work, we demonstrate the spacetime distributions of the electric and magnetic fields of photon. It is concluded that the spacetime distributions of electric and magnetic fields of photon are source dependent. Based on the conclusion obtained in this work, some important potential applications are predicted.
Appendix
1) At the beginning of our universe, there are ten suns in sky (I think this situation only may occur not long after the Big Bang.), which keep the hottest weather in our universe and it is very difficult for the living stuff to survive, not mention for the human being. In order to change this situation, the people think they have to shoot down at least some of suns to make the weather not so hot. So, they ask the powerful man named as “Yi” to finish this task. Yi uses the special bow and arrow shooting down nine suns but the last sun is scared and run away. As a result, the whole world becomes very dark and too cold for the living species to live. Then the people try to call the last sun coming back. They think the sun may not understand the language of the human being, therefore, they figure the music is the international language which the sun may understand. So, the people ask the best singer at that time to sing the most beautiful song and wish the sun can understand and comes back. But the effort of the human being is failed. Then, the people think the animal’s song the sun may understand and like to hear, by trying and error, finally the people find the singing song by cock works. Since then, every morning, as long as cock starts singing, the sun will show up, called sunrise.
2) Mr Confucius is a famous scholar at the ancient time in Chinese history and believed he can answer any kind of questions. One day he heard two kids disputing each other over there and he went over, asking “what puzzle do you have?”, one kid said, “ your honor, Mr Confucius, my opinion is in the morning, the sun is closer to us, because in the morning, the sun is bigger, the bigger, the nearer”. Then second kid said, “your honor, Mr. Confucius, my opinion is in the noon, the sun is closer to us, because in the noon, we feel hotter, the hotter, the nearer”. Based on the limited knowledge about the light at the ancient time, the Confucius can’t answer the question and run away.
Above two stories reflect the effort of the human being in understanding the light at the ancient time.