Gravimetric Studies of Ni Electrodeposition with Additives from Deep Eutectic Solvents Using Electrochemical Quartz Crystal Microbalance EQCM ()
1. Introduction
Electrochemical quartz crystal microbalance (EQCM) has been extensively used in the studying of various electrochemical processes [1] [2] [3] [4] [5]. QCM contains a thin quartz crystal inserted between two metal electrodes that set an alternating electric field across the crystal, resulting in vibrational motion of the crystal at its resonant frequency. This resonant frequency is sensitive to mass changes (and other similarities) of the crystal and its electrodes. The potential to utilize one side of the EQCM as a working electrode in an electrochemical cell while simultaneously measuring tiny mass changes in a nono scale has provided a powerful evaluation to investigate electro-chemical processes concerning thin coatings, incorporating monolayer and sub monolayer films. These researches have supplied precise mechanistic knowledge about film deposition and dissolution, surface morphology changes, and mass changes in thin films caused by redox or other chemical processes [6] [7] [8] [9] [10].
In 1880, Jacques and Pierre Curie discovered that a mechanical stress applied to the surfaces of various crystals, including quartz, Rochelle salt (NaKC4H40s4H20), and tourmaline, provided a correlating to the electrical potential across the crystal whose magnitude was proportional to the applied stress [11]. This response is indicated as the piezoelectric effect. This feature only exists in materials that are acentric; that is, those that crystallize in noncentrosymmetric space groups. Crystal symmetry directs that strain induced in a piezoelectric material by an applied potential of one polarity will be equal and opposite in direction to that produced from the opposite polarity. This is illustrated in Figure 1 for the shear motion of the AT-cut quartz resonator, which contains a thin quartz wafer prepared by slicing through a quartz rod at an angle of approximately 35.25’ with respect to the x axis as depicted in Figure 2. When an electric field is applied
![]()
Figure 1. Graphic description of the converse piezoelectric effect for shear motion. The electric field induces reorientation of the dipoles of the acentric material, causing a lattice strain and shear deformation of the material. Direction of shear is dependent upon the applied potential while the extent of shear strain depends on the magnitude of the applied potential.
![]()
Figure 2. AT and BT cut crystals respond differently to interfacial stress.
the crystal produces a shear strain proportional to the applied potential. In quartz this deformation is elastic. The opposite polarity results an identical strain, but in the opposite direction. It traces that an alternating potential across the crystal produces a vibrational motion in the quartz crystal with amplitude parallel to the surface of the crystal. The electromechanical coupling and resulting stresses therefore rely on the crystal symmetry, the configuration and orientation of the electric field, and the angle of cut of the crystal substrate with respect to its crystallographic axes. Thus, only crystals cut with the proper angles with respect to the crystalline axes exhibit shear displacements.
The fundamental resonant frequency (fo) displaces when at narrow film is loaded on the surface of the quartz crystal as illustrated in Figure 3. Under the conditions that the density and the shear modulus of the film are the same as those of quartz and that the film is uniform (constant density and thickness) and covering the acoustically active area of the whole crystal, the Sauerbrey equation [10] describes the relationship between the resonant frequency shift (Δf) and the added mass (Δm):
(1)
(2)
where ∆m/A the mass deposited per unit area,
density of the quartz,
the viscosity µ0 wave velocity
Rather conveniently for a crystal with a resonant frequency fo of 10 MHz.
(3)
Δf the observed frequency change, Cf the sensitivity factor for the crystal is a constant that depends only on the thickness of the quartz slab and on the intrinsic properties of the quartz or in another words it depends only on physical
![]()
Figure 3. shows the relation between the dissipation change (∆D) and stiffness (rigidity) and also mass change versus frequency change (oscillating crystal). The source is Co AT AB, Q-Sense IncCo AT AB, Q-Sense Inc.
parameters of the crystal sensor [12] [13] [14] [15]. The sharpness of the conductance peak ensures that the feedback loop will be able to “lock in” on a very narrow frequency range. The bandwidth and the resonant frequency determine the quality factor Q (Equation (2)), which is the ratio of the energy stored to the energy lost during oscillation or, equivalently, the inverse of the dissipation factor. For high quality resonators, fc, readily determined from the conductance plot, can be used to determine Q.
(4)
where w is the width of the peak at half its height (HHFW)
(5)
The bandwidth and the resonant frequency determine the quality factor Q (Equation (4)), which is the ratio of the energy stored to the energy lost during oscillation or, equivalently, the inverse of the dissipation factor. For high quality resonators, fc, readily determined from the conductance plot, can be used to determine Q. Alternatively, Q can be expressed as Equation (5), which describes its dependence on L and R. The high values of Q observed for quartz crystals (>l05) can be attributed to the high effective L values coupled with very low values of R.
Sometimes it is suitable to employ the dissipation factor, D, which is simply the reciprocal of the Q factor.
(6)
(7)
where
is the angular frequency at resonance and L1 and R1 are depicted in Figure 4, the components of the series branch correlated with the mechanical prototype in the following manner as shown in Figure 4. L1 is the inertial component related to the displaced mass (m) in the course of oscillation, C1 is the compliance of the quartz element regarded as the energy stored during oscillation (C1), and R1 is the energy dissipation (Ediss) in the course of oscillation attributed to internal friction, mechanical losses in the set up system and acoustical losses to the environment (r). The actual electrical representation of a quartz
![]()
Figure 4. The electrical equivalence of the crystal unit near principle resonance under the assumption that all undesired modes of vibration near the principle resonance are suppressed [12].
resonator also involves a capacitance Co in parallel with this series branch that is simply the static capacitance of the quartz resonator with the electrodes. The series branch is commonly referred to as the motional branch because it is this segment that defines the electromechanical characteristics of the quartz resonator.
For high quality resonators, the resonant frequency fc, readily determined from the conductance graph, can be utilized to evaluate Q. Alternatively, Q can be illustrated in Equation (5), which shows its dependence on L1 and R1. The high values of Q observed for quartz crystals (>l05) can be attributed to the high effective L1 values coupled with very low values of R1. Equation (5) also refers an important feature of the QCM, namely that increasing the value of R will have a corresponding effect on the bandwidth and therefore the stability of oscillation. Thus, energy dissipation to the surrounding medium or to films disabled on the quartz crystal must be regarded in QCM investigations. In summary, the conductance spectrum is a useful diagnostic tool because a shift in frequency indicates changes in mass at the surface of the quartz crystal while changes in energy dissipation can be determined from the bandwidth [16].
2. Admittance/Impedance Behavior of Quartz Resonators
Impedance analysis involves the measurement of current at a known applied voltage over a specified range of frequencies. This is commonly accomplished with impedance analyzers such as the Hewlett-Packard 4192 network analyzer, the more sophisticated 4194A model or Hewlett-PackardHP87512A network analyzer connected to a Hewlett-PackardHP87512A transmission/reflection unit which used in this study. These instruments are capable of measurement of impedance (Z), phase angle (e), admittance (Y), conductance (G), and susceptance (B), as well as other parameters. The properties of the quartz resonator, particularly the properties of the series branch, can be described conveniently by the admittance of the resonator (Equation (8)). Each component of the equivalent circuit representation has an admittance. Most importantly, the admittance of Co, C1 and L1 are frequency dependent and the current flow through the resonator will depend upon the frequency as well as the applied voltage. The frequency-dependent properties of the resonator can be discerned from admittance plots, in which the abscissa represents the real part of the admittance and the ordinate the imaginary component j [17].
(8)
(9)
The resultant of real number and imaginary vectors can be applied to calculate the magnitude of the admittance (|Y|) as depicted in Equation (9) [17].
Experimental Details
Preparation of IL
Choline chloride [HOC2H4N(CH3)3Cl] (ChCl) (Aldrich 99%) was recrystallized from absolute ethanol, filtered and dried under vacuum. Urea (Aldrich > 99%) was dried under vacuum before use. Ethylene glycol (EG) (Aldrich 99%+), nickel chloride hex hydrate, ethylenediamine (en) and acetylacetonate (acac) (all Aldrich) were all used as received. The eutectic mixtures were formed by stirring the two components together, in the stated proportions, at 75˚C until a homogeneous, colourless liquid formed. And the concentrations of NiCl2·6H2O in both ionic liquid electrolyte were maintained 0.2M.
Gravimetric analysis
Crystal impedance spectra were recorded using a Hewlett Packard HP8751A network analyzer, connected to a HP87512A transmission/reflection unit via 50 ohm coaxial cable as detailed elsewhere. The working electrode was a thin gold film evaporated onto a 10 MHz quartz crystal with a unpolished “frosted” finish (purchased from the International Crystal Manufacturing Co. Oklahoma City, USA). The piezoelectric active electrode area was 0.23 cm2.
The measured data were fitted to a Lorentzian equivalent circuit model, Equation (10), incorporating the in-phase impedance, inductance and centre frequency, with an iterative difference method using Microsoft Excel. The fitting procedures used are described in depth in the literature. In order to improve the temporal resolution, network analyzer data acquisition was controlled by a computer running HP VEE. This program was capable of recording admittance spectra every 2 - 3 s. The crystal was placed into a cell such that one face of the crystal was exposed to the solution and one face was exposed to air. The electrodes used to complete the electrochemical cell were platinum flag and silver wire as reference electrode. EQCM experiments were performed at room temperature (typically 20˚C - 23˚C) except otherwise stated.
(10)
where
is the mesure of admittance curve as a function of applied frequency
(and
),
is the real component of the impedance (Z), L/Henry is the inductance, 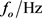 is the centre frequency and
is the centre frequency and 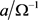 is the base line offset. The latter was used during fitting to compensate for variations in the static calibration of the network analyser (Figure 5).
is the base line offset. The latter was used during fitting to compensate for variations in the static calibration of the network analyser (Figure 5).
![]()
Figure 5. The experimental setup for Ni electrodeposition from Msc. Thesis O. u. Motta 2005.
3. Result and Discussion
The electrochemistry of most p and d block elements has been studied in both of these liquids and the authors have found that metals in groups 3 - 5 (Sc-V) cannot be deposited within the potential window of the ionic liquid. The majority of the remaining elements (Cu, Ag, Zn, Hg, In, Sn and Bi) show reversible deposition and stripping responses. Those in groups 6 - 8 (Cr-Fe) can be reduced but not stripped whereas Co, Ni and Pdall give a quasi-reversible deposition response. The current efficiency obtained from the mass-charge data shown in Figure 6(a) for nickel deposition from ethaline was found 100%, while the current efficiency for nickel deposition from reline is about 70%, which is represented in Figure 6(b). This distinction could be attributed to the viscosity factor, where the viscosity of reline (1 Chol. Chloride: 2 urea) is larger than the viscosity of ethaline (1 Chol. Chloride: 2ethylene glycol) [18]. The rate of depositions of Ni coating from both ethaline and reline ionic liquids were calculated from Figure 6(c) and Figure 6(d) respectively. Figure 6(g) shows the plot of the theoretical Q factor versus the data Q factor, where they are in a good agreement in case of Ni deposits from ethaline, however, in case of the reline, the Q factors (theoretical and data) are noisy but reasonably in good agreement as shown in Figure 6(h). The current efficiency of Ni deposition from ethaline in the presence of ethylene diamine was obtained from Figure 7(a) as shown in Table 1 which was less than that of which obtained from ethaline only. The lowering in current efficiency is often certain attributed to proton reduction [19].The rate of nickel deposition in the presence of ethylene diamine was found 10 ng/s as seen in Table 1. Figure 7(b) represents mass/charge plot for electrodeposition of nickel from reline with added ethylene diamine (en) is fairly noisy due to the low resonant amplitude of the quartz crystal in the DES media. There is a sharp increase in mass in a very small period of time (~4 minutes as determined from Figure 7(d)) then the loading of nickel mass is stopped as the charge passes and this may be due to the protonation. The electrodeposition of nickel from ethaline in the presence of acac is depicted in Figure 8(a) where the current efficiency was found 37% which is reasonably low and the rate of the nickel deposition is also very slow as shown in Table 1. In case of electrodeposition of nickel from reline with added acac has similar profile, obtained within the presence of ethylene diamine from reline, but different in the total mass obtained. The charge where the mass was from obtained in the presence of ethylene diamine is about ten folds the mass produced with added acac. Comparison of the mass/charge
![]()
Table 1. Current efficiencies of Ni deposition from Ethaline and Reline at concentration of 0.2 M NiCl26H2O in the absence and presence of three equivalents of both en and acac at applied potential of 2.5 V.
![]()
![]()
Figure 6. Shows the electrodeposition of nickel deposits from ethaline and reline without additives.
![]()
Figure 7. Shows the electrodeposition of nickel deposits from ethaline and reline with added en.
data for the ILs with and without the addition of en and acac shows that when both en and acac are added, there is a significant decrease in current and the associated growth rate, suggesting that the en and acac stop the formation and
![]()
Figure 8. Represents the electrodeposition of nickel deposits from ethaline and reline with added acac.
growth of Ni nuclei. It was also found that after the addition of en and acac, the process was no longer mass transport limited, indicating that the growth mechanism had changed [20].
4. Conclusion
A method based on the use of in situ electrochemical quartz crystal microbalance (EQCM) was used to investigate the coulombic efficiency and growth mechanism of the of nickel deposition from ethaline and reline electrolytes. The coulombic efficiencies are 100% for nickel deposits from ethaline in absence of additives, 70% for nickel deposits from reline in absence of complex agents, 54% and 37% for nickel deposits from ethaline in the presence of ethylene diamine and acetylacetonate respectively. For nickel deposits from reline in the presence of ethylene diamine and acetylacetonate there is a sharp increase in mass loaded in very short interval time and then it stops loaning mass this due to protonation. The exact mechanism for these observations and difference in kinetics of Ni electrodeposition from ethaline and reline with and without additives are not clear and will be subjected to further investigations.