Quantum Cosmological Tetration of Time

Angus McCoss

Kilbrandon House, PA34, UK.

DOI: 10.4236/jhepgc.2020.62016                

Abstract

In an original quantum cosmology model, the scale factor evolution describing Hubble expansion is solely determined by the third tetration of time. The model exhibits early accelerating expansion, mid-time decelerating expansion, and late accelerating expansion. The substrate of reality, coined the “Graphiverse”, is a quantum-classical information processing network, represented by a learning deep generative graph. It comprises two complementary sub-graphs which are the substrates of a perceived rendering and a dark rendering of the emergent physical universe. Four temporal registers that count change (i.e. dimensions of time) are defined: system time, classical complexity time, quantum-classical correlation (or discord) time, and quantum coherence time. The cosmological scale factor evolves through a right-associative iterative exponentiation of these times. In the first (right) exponentiation, quantum-classical correlation (or discord) time is the base and its exponent is quantum coherence time. In the second (left) exponentiation, classical complexity time is the base and its exponent is the first (right) exponentiation. The four temporal registers that count change self-synchronize and equalize the four dimensions of time. The model provides a nexus for a new discussion about time and quantum gravity.

Keywords

Cosmology, Quantum Information, Quantum Gravity, Complexity, Graphiverse

1. Introduction

This research note is motivated to address problems of time and quantum gravity [1]. Quantum theory and general relativity are each an accurate formalization of physics, however their unification remains obscure. Time is absolute in quantum theory, whilst dynamical in general relativity. The passage of time is a familiar experience, yet leading scientists and philosophers continue to debate its meaning and significance [2] [3].

The reader is referred to Hu et al. [4] for a review and contemporary bibliography of quantum coherence and quantum correlations. Seminal insights on this subject are presented in the works of Zurek [5] [6]. For an introduction to the theory of complex systems see Thurner et al. [7] and for further background refer to Zurek’s compilation on complexity, entropy and the physics of information [8].

The following section sets out the formulation of an original quantum cosmology model in which the scale factor evolution [9], $a\left(t\right)$, is solely determined by the third tetration of time, $t^{t^t}$. That section also provides a physical, quantum cosmological, interpretation of the formulation and discusses how the universe is experienced via agents’ perceptual interfaces. Interpretations of the chronology of the model evolution are given in the subsequent section and succinct conclusions wrap up this note.

2. Formulation

The standard cosmological scale factor is the ratio of the proper distance, say between two galaxies, at a time counted from the Big Bang, divided by the distance at the reference time, now. The scale factor, spatial curvature and the energy density of the universe are related by the Friedmann equations, derived from Einstein’s field equations of gravitation, where gravity is a geometric property of space and time [9]. An original model cosmological scale factor evolution is defined here which provides a nexus to relate these successful equations of gravitation to the quantum foundations of time.

As a preliminary condition, let us assume information is processed in a quantum-classical network [10], represented by a learning deep generative graph [11], that is the substrate of reality. This substrate, here coined the “Graphiverse”, $\mathcal{G}$, comprises two complementary sub-graphs which are the substrates of: 1) a specific perceived rendering, $\mathcal{U}$, that is our emergent physical universe, explored by its multiple agents; and 2) a dark rendering, $\mathcal{D}$, which is hidden from the specific sensory, technological and neural interactions of the multiple agents in $\mathcal{U}$ :

$\mathcal{G}\mapsto \{\begin{array}{l}\mathcal{D}\\ \mathcal{U}\end{array}$ (2.1)

The dark rendering, $\mathcal{D}$, (2.1) is placed above the perceived rendering, $\mathcal{U}$, that is our emergent physical universe, to emphasise that $\mathcal{D}$ is dominant. Hoffman and co-workers [12] make a reasoned claim that Darwin’s evolution by natural selection tunes the perceptual interfaces of agents to maximise their fitness in $\mathcal{U}$, over attaining enlightenment about all truths in $\mathcal{G}$. The perceived rendering, $\mathcal{U}$, that appears as our virtual physical universe, only provides a tantalising glimmer of that deep enlightenment, whilst keeping us pragmatically focused on passing on our genes, knowledge and values. Future scientific progress, particularly in high energy physics and cosmology, is expected to unveil the dark rendering, $\mathcal{D}$, and hence reveal more of the Graphiverse, $\mathcal{G}$, that is the complete substrate of reality.

Let us now define and consider the sets T, (2.2) and H, (2.3):

$T=\left\{\Delta t,2\Delta t,3\Delta t,\cdots ,n\Delta t-2\Delta t,n\Delta t-\Delta t,n\Delta t\right\}$ (2.2)

$H=\left\{\Delta t,2\Delta t,3\Delta t,\cdots ,t_H-2\Delta t,t_H-\Delta t,t_H\right\}$ (2.3)

$t_H=1/H_0$ (2.4)

$t=\left|T\right|/\left|H\right|,t\in \mathbb{Q},n\in \mathbb{Z}$ (2.5)

where $\Delta t$ is a minimum computational timestep in the evolution of the Graphiverse; Hubble time, $t_H$, is the reciprocal of the present value of the Hubble parameter, $H_0$ (2.4); and $\left|T\right|$ and $\left|H\right|$ are respectively the integer cardinalities (number of elements) of the sets T and H. Their ratio, $\left|T\right|/\left|H\right|$, defined as system time, t, (2.5) is an element of the set of rational numbers, $\mathbb{Q}$, and is dimensionless and countable. The number n is an element of the set of integers, $\mathbb{Z}$.

The four-colour theorem [13] states the vertices of every planar graph can be identified with at most four labels (generalisation of colours) where no adjacent vertices have the same label. Let us consider the four labels as four 1-dimensional temporal registers that count change, as times on rational number lines, during the information symmetry-breaking evolution of the Graphiverse.

The four temporal registers, or times, are:

1) system time, $t$ ;

2) classical complexity time, $t_{\text{Δ}CC}$ ;

3) quantum-classical correlation (or discord) time, $t_{\text{Δ}QC}$ ; and

4) quantum coherence time, $t_{\text{Δ}QQ}$

An original formulation of cosmological scale factor $a\left(t\right)$ is conjectured:

$a\left(t\right)=t_{\text{Δ}CC}{}^{\left(t_{\text{Δ}QC}{}^{t_{\text{Δ}QQ}}\right)}$ (2.6)

where spontaneous self-synchronisation [14] causes all registers to equalize with system time:

$t=t_{\text{Δ}CC}=t_{\text{Δ}QC}=t_{\text{Δ}QQ}$ (2.7)

From (2.6) and (2.7) the main equation of this paper (2.8) is boxed:

$\boxed{a\left(t\right)=t^{t^t}}$ (2.8)

where the first derivative $\stackrel{\dot{}}{a}\left(t\right)$ :

$\stackrel{\dot{}}{a}\left(t\right)=t^{t^t}\left(t^t\left(\log \left(t\right)+1\right)\log \left(t\right)+t^{t-1}\right)$ (2.9)

and second derivative $\ddot{a}\left(t\right)$ :

$\begin{array}{c}\ddot{a}\left(t\right)=t^{t^t}{\left(t^{t-1}+t^t\log \left(t\right)\left(\log \left(t\right)+1\right)\right)}^2+t^{t^t}(t^{t-1}\log \left(t\right)+t^{t-1}\left(\log \left(t\right)+1\right)\begin{array}{c}\\ \end{array}\\ +t^{t-1}\left(\frac{t-1}{t}+\log \left(t\right)\right)+t^t\log \left(t\right){\left(\log \left(t\right)+1\right)}^2)\end{array}$ (2.10)

which are plotted in Figures 1-7.

Equation (2.6) is a right-associative third tetration, or iterative exponentiation, of registered counts of timesteps. The value of $a\left(t\right)$ is calculated right to left, or top to bottom. In the first exponentiation, top right bracket, $t_{\text{Δ}QC}$ is the base and $t_{\text{Δ}QQ}$ is its exponent. In the second exponentiation, $t_{\text{Δ}CC}$ is the base and $\left(t_{\text{Δ}QC}{}^{t_{\text{Δ}QQ}}\right)$ is its exponent.

Consider this tetration as compounding information symmetry-breaking in the Graphiverse. The right-associative process runs through the entire quantum-classical computational network, represented by a learning deep generative graph, comprising counted changes in quantum coherence, compounding counted changes in quantum-classical correlations (or discord), that all together compound counted changes in classical complexity. As system time, t, accumulates then quantum coherence symmetries break (decoherence), quantum-classical correlation symmetries break (decorrelation) and classical symmetries break (complexity evolution).

In the Graphiverse, self-synchronisation of temporal registers (2.7) with concomitant complexity growth (2.6) relates to a gain in computational efficiency (Fermat’s principle of least time) with a loss in symmetry. (Note a similarity to emergent optical refraction). Nonetheless, the loss in symmetry during evolution of the Graphiverse in system time creates a rich and existential perceived rendering, $\mathcal{U}$, for its multiple agents. Furthermore, the corresponding right-associative iterative exponentiation of time greatly compounds the perceived expansion of cosmological scale, (2.6) and (2.8). The formulation (2.8) models the expansion of our perceived universe, with early acceleration, mid-time deceleration, and late acceleration (Figures 1-7).

Integration of the complex wave packet (Figure 2, Figure 4 & Figure 7), in negative time, i.e. where $t<0$, gives constants at the limit in far negative time, $\underset{t\to -\infty }{\lim }$ :

$\underset{t\to -\infty }{\lim }\left(t+{\displaystyle {\int }_t^0{t}^{t^t}\text{d}t}\right)\approx 0.62284+0.54701i$ (2.11)

$\underset{t\to -\infty }{\lim }\left(t+{\displaystyle {\int }_T^0{\left|t^{t^t}\right|}^2\text{d}t}\right)\approx 1632.76$ (2.12)

The integrand in (2.11) is the scale factor evolution given by the third tetration of time (2.8), and the integrand in (2.12) is the square of the magnitude of the third tetration of time.

A generalised Puiseux series expansion of (2.8) at $t=0$ is given by:

$\begin{array}{c}{t}^{t^t}\approx t+t^2{\log }^2\left(t\right)+\frac{1}{2}{t}^3{\log }^3\left(t\right)\left(\log \left(t\right)+1\right)\\ +\frac{1}{6}{t}^4{\log }^4\left(t\right)\left({\log }^2\left(t\right)+3\log \left(t\right)+1\right)\\ +\frac{1}{24}{t}^5{\log }^5\left(t\right)\left({\log }^3\left(t\right)+6{\log }^2\left(t\right)+7\log \left(t\right)+1\right)\\ +\frac{1}{120}{t}^6{\log }^6\left(t\right)\left({\log }^4\left(t\right)+10{\log }^3\left(t\right)+25{\log }^2\left(t\right)+15\log \left(t\right)+1\right)+O\left(t^7\right)\end{array}$ (2.13)

Figure 1. Blue solid curve: plot of scale factor $a\left(t\right)=t^{t^t}$ versus time, t. Green dashed line: tangent, $a\left(t\right)=t$, at time now, $t=1$, to the scale factor curve (blue). Time $t=0$ corresponds to the Big Bang. Scale factor $a\left(t\right)$ evolves through system time, t, from early accelerating expansion, through decelerating expansion, to late accelerating expansion. For $t>0$ the scale factor $a\left(t\right)$ is monotonically increasing. The plot illustrates real values where $t>0$. Model scale factor evolution $a\left(t\right)$ (blue) and its tangent (green dashed) at time now, $t=1$, intersect the time axis at $t=0$. See Table 1 for numerical analyses.

Figure 2. Plot of scale factor $a\left(t\right)$ versus system time, t. Time $t=0$ corresponds to the Big Bang and time $t=1$ corresponds to the time now. The plot illustrates real (blue) and imaginary (red dashed) values in negative and positive time, t. In negative time, $t<0$, $a\left(t\right)$ is characterised by a wave packet with positive and negative values, whereas in positive time, $t>0$, $a\left(t\right)$ is always positive and monotonically increasing (Figure 1). See Table 1 for numerical analyses.

Figure 3. Plot of the first derivative of the scale factor, $\stackrel{\dot{}}{a}\left(t\right)$ versus time, t. Time $t=0$ corresponds to the Big Bang and time $t=1$ corresponds to the time now. The first derivative of the scale factor $\stackrel{\dot{}}{a}\left(t\right)$ evolves through time, t, from early accelerating expansion, through decelerating expansion to late accelerating expansion. Extrema at $t=0.064$ and $t=0.668$ are shown. The plot illustrates real values where $t>0$. See Table 1 for numerical analyses.

Figure 4. Plot of the first derivative of the scale factor, $\stackrel{\dot{}}{a}\left(t\right)$ versus time, t. Time $t=0$ corresponds to the Big Bang and time $t=1$ corresponds to the time now. The plot illustrates real (blue) and imaginary (red dashed) values in negative and positive time, t. In negative time, $t<0$, $\stackrel{\dot{}}{a}\left(t\right)$ is characterised by a wave packet with positive and negative values, whereas in positive time, $t>0$, $\stackrel{\dot{}}{a}\left(t\right)$ is always positive (Figure 3). See Table 1 for numerical analyses.

Figure 5. Plot of the second derivative of the scale factor, $\ddot{a}\left(t\right)$ versus time, t. The second derivative of the scale factor $\ddot{a}\left(t\right)$ evolves through time, t, and explodes at $t=0$. Time $t=0$ corresponds to the Big Bang and time $t=1$ corresponds to the time now. The plot illustrates real (blue) and imaginary (red dashed) values in negative and positive time near $t=0$. See Table 1 for numerical analyses.

Figure 6. Plot of the second derivative of the scale factor, $\ddot{a}\left(t\right)$ versus time, t. Time $t=0$ corresponds to the Big Bang and time $t=1$ corresponds to the time now. The second derivative of the scale factor $\ddot{a}\left(t\right)$ evolves through time, t, from early accelerating expansion, through mid-time decelerating expansion (negative $\ddot{a}\left(t\right)$ ), to late accelerating expansion. The plot illustrates real values where $t>0$ and illustrates the deceleration extremum at $t\approx 0.162$. See Table 1 for numerical analyses.

Figure 7. Plot of the second derivative of the scale factor, $\ddot{a}\left(t\right)$ versus time, t. Time $t=0$ corresponds to the Big Bang and time $t=1$ corresponds to the time now. The plot illustrates real (blue) and imaginary (red dashed) values in negative and positive time, t. In negative time, $t<0$, $\ddot{a}\left(t\right)$ is characterised by a wave packet with positive and negative values. See Table 1 for numerical analyses.

Table 1. Model cosmology chronology from numerical analyses and study of Figures 1-7.

The Fourier transform of scale factor evolution $a\left(t\right)$ (2.8) with frequency variable ω is given by:

${\mathcal{F}}_t\left[t^{t^t}\right]\left(\omega \right)=\frac{1}{\sqrt{2\pi }}{\displaystyle {\int }_{-\infty }^{\infty }{t}^{t^t}{\text{e}}^{i\omega t}dt}$ (2.14)

3. Model Cosmology Chronology

Numerical analyses of $a\left(t\right)$, $\stackrel{\dot{}}{a}\left(t\right)$ and $\ddot{a}\left(t\right)$ and a study of the plots in Figures 1-7 leads to Table 1 which sets out the model cosmology chronology. The model cosmology chronology is characterised by 7 stages (below, sub-sections 3.1 to 3.7). Model time is anchored by definition: $t=0$ corresponds to the Big Bang, and $t=1$ marks the time now. The model scale factor curve $a\left(t\right)$ and its tangent at time now, $t=1$, both intersect the time axis at $t=0$ (Figure 1). A universal approach to scaling model time to astrophysical time would use a full set of independently determined astrophysical ages of model extrema ( $\max \stackrel{\dot{}}{a}\left(t\right)$, $\min \stackrel{\dot{}}{a}\left(t\right)$ and $\min \ddot{a}\left(t\right)$ ) as event markers.

3.1. Far Negative Time

The scale factor evolution $a\left(t\right)$ during model times less than negative 4 from the Big Bang has complex solutions. The real part, $Re\left[a\left(t\right)\right]\approx 1$, and the imaginary part, $Im\left[a\left(t\right)\right]\approx 0$. Far negative time is the most quiescent stage of the model cosmology, in terms of scale factor dynamics.

3.2. Near Negative Time

The scale factor evolution $a\left(t\right)$ during model times less than zero and greater than negative 4 from the Big Bang has complex solutions. The real part, $Re\left[a\left(t\right)\right]$, and the imaginary part, $Im\left[a\left(t\right)\right]$, form a complex wave packet (Figure 2, Figure 4 & Figure 7).

This stage of the development of the universe is conjectured to involve the superposition of multiple scale factor oscillations, such as given in a generalised Puiseux series expansion (2.13), or by the Fourier transform (2.14), or some other wave packet decomposition in time, that combine to establish a single wave packet in a localised interval of near negative time.

3.3. Big Bang

The Big Bang occurs at model time $t=0$. It is interpreted to be characterised by the explosion of $\ddot{a}\left(t\right)$ (Figure 5) at $t=0$ when real scale $Re\left[a\left(t\right)\right]$ is proposed to spontaneously emerge from the near negative time complex wave packet (Figure 2, Figure 4 & Figure 7).

In contrast to the complex wave packet scale factor evolution in negative time, the Big Bang event at $t=0$ heralds monotonically increasing scale factor evolution through positive time. The scale factor evolution in (2.8) is strongly asymmetric about $t=0$. The scale factor evolution becomes spontaneously real valued for $t>0$ and according to Barbour et al. a gravitational arrow of time [15] emerges with information growth. The gravitational arrow of time orders self-organization in the subsequent stage of early accelerating expansion. Whether that arrow of time existed in negative time before the Big Bang is an open question.

It is conjectured here that the complex wave packet scale factor evolution in near negative time represents a hyper-massive quantum proto-universe in superposition before the Big Bang. The constants (2.11) (2.12) at the limit in far negative time, of the integrals of the complex wave packet, may relate to the conjectured mass-energy of the hyper-massive quantum proto-universe.

Whether any such hyper-massive quantum proto-universe before the Big Bang could lead to entanglement of temporal orders between time-like events is a profound question for modern physics and the reader is referred to Zych et al. [16] for a seminal discussion on Bell’s theorem for temporal order. Researchers are encouraged to build on their important work, perhaps towards new physics. As Zych and her co-workers emphasise, pre-defined local variables cannot be used to describe temporal order and the classical concept of a causal structure is unsound in any framework that respects the basic principles of general relativity and quantum mechanics. Extending the principles of these great theories into the realm of negative time before the Big Bang may help us formulate any such new physics.

3.4. Early Accelerating Expansion

In the model cosmology, in positive time immediately following the Big Bang, the evolution of $a\left(t\right)$ is characterised by early accelerating expansion. The homogeneous and isotropic nature of the present universe (cosmological principle) is interpreted to be a consequence of this primordial exponential expansion, which starts at $t=0$ and ends at $t\approx 0.064$ after the Big Bang, at redshift $z\approx 9.03$ ) (Figure 3).

Cosmological decoherence (from quantum coherence to quantum-classical correlation) [4] [5] [6] is the dominant mechanism during this stage. The end of this stage marks the end of the Dark Ages, reionization and large-scale structuration of the early universe.

3.5. Decelerating Expansion

The scale factor evolution $a\left(t\right)$ during model times between at $t\approx 0.064$ after the Big Bang, redshift $z\approx 9.03$ and $t\approx 0.668$ after the Big Bang, redshift $z\approx 0.36$ ) is marked by decelerating expansion. The extremum of deceleration occurs at model time $t\approx 0.162$ after the Big Bang, redshift $z\approx 2.87$ (Figure 6).

This model stage corresponds to a matter dominated interval in the evolution of the universe when emergent gravitational attraction appears to constrain the rate of expansion. The foundational constraint is however the third tetration of time, $a\left(t\right)=t^{t^t}$. The end of this stage occurred during the Hadean Eon on our planet Earth, when the chemical conditions for abiogenesis emerged.

3.6. Late Accelerating Expansion

We are presently ( $t=1$, redshift) in the late accelerating expansion stage of the model cosmology. Since model time 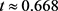after the Big Bang, redshift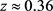, and through the time now to future near positive time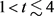, the effects of right-associative iterative exponentiation (2.6) rapidly expand emergent space through time. Compounding cosmological scale, with growing complexity, approaches runaway rates of late accelerating expansion (Figure 2, Figure 4 & Figure 7).

3.7. Far Positive Time

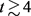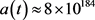One might reasonably consider that late accelerating expansion in far positive time after the Big Bang would lead to a form of “Big Rip” [17]. Indeed, in the model, when we obtain a value of which equals the number of Planck volumes in the currently observable universe. Iterated exponential expansion in extremely far positive time becomes intractable.

4. Conclusions

This quantum cosmology model proposes that scale factor evolution is defined by the third tetration of time, 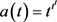(2.8). The model proposes time is not at all peculiar, but space is virtual. Computational timesteps register changes in the substrate of reality, here coined the “Graphiverse”, that is a quantum-classical information processing network, represented by a learning deep generative graph. Virtual space emerges from a naturally selected specific perceived rendering of a subgraph. A dominant complementary subgraph has a dark rendering, which is presently hidden from our limited faculties of observation.

The tetration of time is considered as compounding information symmetry-breaking in the Graphiverse. The right-associative process runs through the Graphiverse and comprises counted changes in quantum coherence, compounding counted changes in quantum-classical correlations (or discord), that all together compound counted changes in classical complexity. As system time accumulates then quantum coherence symmetries break (decoherence), quantum-classical correlation symmetries break (decorrelation) and classical symmetries break (complexity evolution), in an iterative exponentiation. In the perceived rendering, since the Big Bang, we observe emergent space undergoing early accelerating expansion, mid-time decelerating expansion, and late accelerating expansion. The model also provides solutions for cosmological scale evolution before the Big Bang. It is conjectured that a complex wave packet in the scale factor evolution in near negative time represents a hyper-massive quantum proto-universe in superposition before the Big Bang.

The gravitational dynamics of the cosmos are emergent in this model. The model formulation of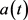, as a function solely of time and in the quantum information paradigm, could be substituted into the Friedmann equations, to relate this model to Einstein’s field equations of gravitation. Since the model formulation is constructed in the quantum information paradigm, it could also be substituted into quantum theory. Future research may connect such substitutions to provide a simple nexus for a new discussion about quantum gravity and time. Clearly there is scope for more multidisciplinary research into these original ideas.

Acknowledgements

This original research is self-funded and I thank my reviewers and editors for their valuable support.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Kiefer, C. (2017) Does Time Exist in Quantum Gravity? In: Towards a Theory of Spacetime Theories, Birkhäuser, New York, 287-295. https://doi.org/10.1007/978-1-4939-3210-8_10
[2]	Rovelli, C. (2019) The Order of Time. Riverhead Books.
[3]	Smolin, L. (2013) Time Reborn: From the Crisis in Physics to the Future of the Universe. HMH.
[4]	Hu, M.L., Hu, X., Wang, J., Peng, Y., Zhang, Y.R. and Fan, H. (2018) Quantum Coherence and Geometric Quantum Discord. Physics Reports, 762-764, 1-100. https://doi.org/10.1016/j.physrep.2018.07.004
[5]	Zurek, W.H. (2003) Decoherence, Einselection, and the Quantum Origins of the Classical. Reviews of Modern Physics, 75, 715. https://doi.org/10.1103/RevModPhys.75.715
[6]	Ollivier, H. and Zurek, W.H. (2001) Quantum Discord: A Measure of the Quantumness of Correlations. Physical Review Letters, 88, Article ID: 017901. https://doi.org/10.1103/PhysRevLett.88.017901
[7]	Thurner, S., Hanel, R. and Klimek, P. (2018) Introduction to the Theory of Complex Systems. Oxford University Press, Oxford. https://doi.org/10.1093/oso/9780198821939.001.0001
[8]	Zurek, W.H. (2018) Complexity, Entropy & the Physics of Information. CRC Press, Boca Raton. https://doi.org/10.1201/9780429502880
[9]	Weinberg, S. (2008) Cosmology. Oxford University Press, Oxford.
[10]	McClean, J.R., Romero, J., Babbush, R. and Aspuru-Guzik, A. (2016) The Theory of Variational Hybrid Quantum-Classical Algorithms. New Journal of Physics, 18, Article ID: 023023. https://doi.org/10.1088/1367-2630/18/2/023023
[11]	Li, Y., Vinyals, O., Dyer, C., Pascanu, R. and Battaglia, P. (2018) Learning Deep Generative Models of Graphs.
[12]	Hoffman, D.D., Singh, M. and Prakash, C. (2015) The Interface Theory of Perception. Psychonomic Bulletin & Review, 22, 1480-1506. https://doi.org/10.3758/s13423-015-0890-8
[13]	Wilson, R. (2013) Four Colors Suffice: How the Map Problem Was Solved-Revised Color Edition (Vol. 30). Princeton University Press, Princeton.
[14]	Strogatz, S. (2004) The Emerging Science of Spontaneous Order. Penguin Press Science, London.
[15]	Barbour, J., Koslowski, T. and Mercati, F. (2014) Identification of a Gravitational Arrow of Time. Physical Review Letters, 113, Article ID: 181101. https://doi.org/10.1103/PhysRevLett.113.181101
[16]	Zych, M., Costa, F., Pikovski, I. and Brukner, C. (2019) Bell’s Theorem for Temporal Order. Nature Communications, 10, Article No. 3772. https://doi.org/10.1038/s41467-019-11579-x
[17]	Caldwell, R. (2002) A Phantom Menace? Cosmological Consequences of a Dark Energy Component with Super-Negative Equation of State. Physics Letters B, 545, 23-29. https://doi.org/10.1016/S0370-2693(02)02589-3